面向智能制造技术的绿色汽车装配线布局仿真与分析

郭 笛

（大连东软信息学院，辽宁 大连 116023）

0 引言

绿色汽车产业的转型升级是实现碳达峰、碳中和宏大愿景的一个重要组成部分，其中装配线工艺流程中运用AGV、机械手等进行智能化改造能够大大提升装配过程的自动化，降低劳动成本，提高绿色汽车生产效率。装配线布局是装配线设计过程中的重要环节，需要参考设备布置、动力设置、区域划分及运输路径等多重因素，是困扰绿色汽车产业动能转换及智能化升级的难题之一。

现有的研究在装配线规划问题上已经取得了丰硕成果，但是仍有一些问题需要扩大深度或广度：一是装配线的规划涉及到多种复杂因素，难以通过数学规划模型实现最优解，可以尝试借助系统化离散型的仿真工具对装配线进行仿真模拟；二是装配线的布局是与工艺流程紧密相关的业务模块，但是相对研究较少，缺乏足够的基础理论资料；三是运用仿真工具运行后针对数据的分析多以主观分析为主，缺乏与定量方法相结合的严谨分析流程。因此，鉴于现有研究的情况和发展需求，本文在分析绿色汽车装配流程的基础上，运用层次Petri网建立装配流程作业静态仿真模型，根据映射规则将其转化为FlexSim动态仿真，并运用定量化分析工具分析仿真数据和结果，以期解决绿色汽车装配线布局规划问题。

1 问题描述

CW公司是一家电动车生产制造企业，目前，电动车的装配过程主要以人工为主，每道工序需要的零部件从生产、筛选到原料仓，再到线上转运、装配等一系列的重复工作需要大量的劳动力，造成较高的人工和管理成本。而且，由于人工素质参差不齐导致装配生产线相对不稳定，生产效率较低，且出错率较高。为了解决这些问题，该公司拟采用自动化的装配生产线，引入AGV小车进行物料的输送、搬运，引入自动化传送带完成工序间料件的转运，引入机械手完成部分自动组装和检测。然而，装配线该如何布局是该公司亟待解决的问题之一。

常见的装配线布局有直线型、直角型、U型、S型四种。每种方式各有优缺点和适用的情况。其中，直线型作为最简单的一种布局方式，会显著的增加物流成本，已经基本被淘汰；直角型对空间的利用率有限，无法满足电动汽车装配这种复杂流程对于空间的要求。因此，本文在研究中主要以U型和S型两种布局方式作为对照研究对象，分析CW电动汽车制造公司最适用的布局。

2 装配工艺层次Petri网模型构建

2.1 装配工艺流程

由于绿色汽车多采用电能新能源，与传统燃油车相比，在动力总成部分，取消了发动机安装、油管油箱安装、加注机油等工序，增加了驱动电机安装、电池安装、高压线束安装等工序。虽然从装卸工艺上来说，这些改变不会对绿色汽车的总装工艺产生很大的影响。但是，在工作站进行布置时，需要增加驱动电池装配工作站和快速充电工作站，并为工作站配备专用的物流通道。

2.2 层次Petri网模型

2.3 建立绿色汽车装配层次Petri网模型

在调研的基础上，结合装配的工艺流程，构建了顶层、第二层、第三层Petri网模型，如图1所示。各层网络中各个库所、变迁代表的含义见表1。

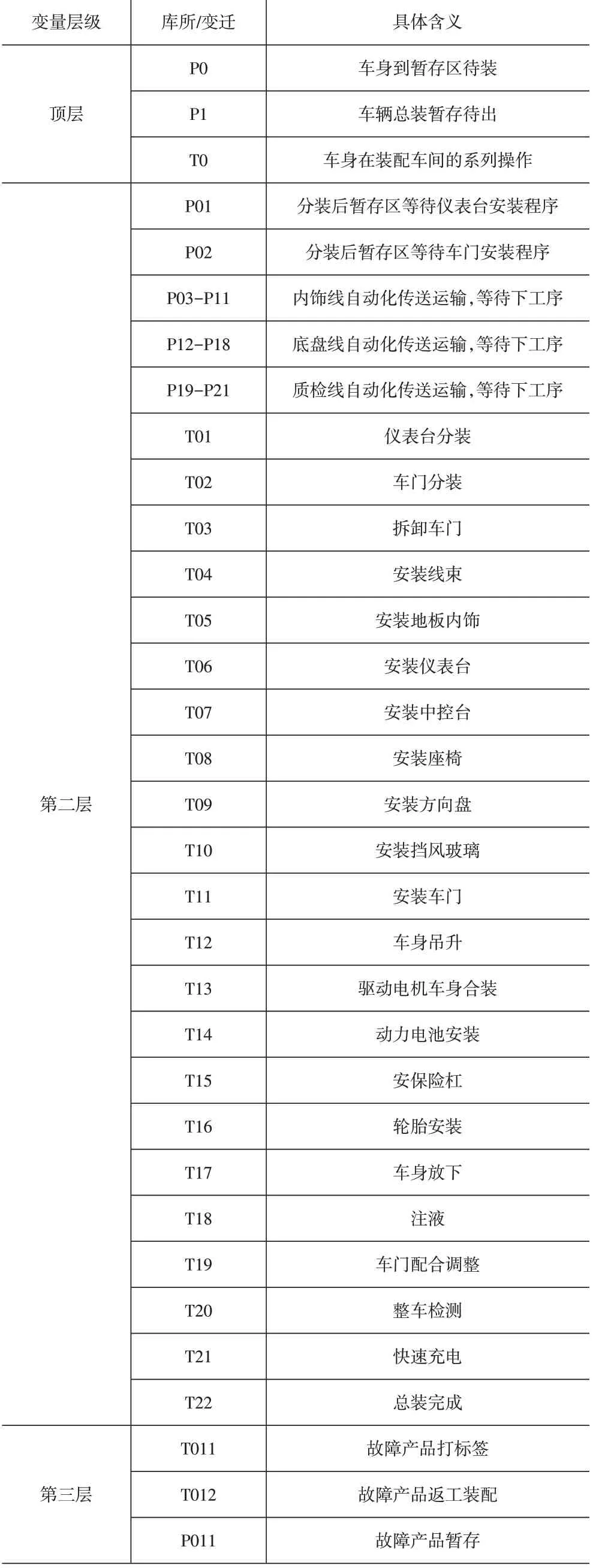
表1 层次Petri网模型各层库所、变迁含义

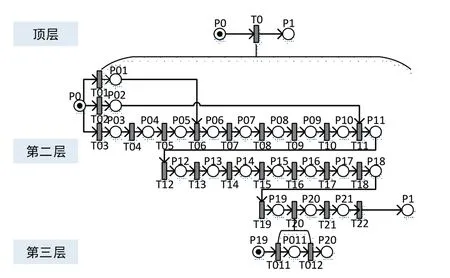
图1 绿色汽车装配层次Petri网模型

3 基于FlexSim的装配线布局建模仿真

3.1 基于装卸工艺的布局方案

在明确装卸工艺流程的基础上，根据CW公司装配车间的面积情况，将装配车间划分为空车身放置区、大物放置区、小物放置区、内饰线装配区、底盘线装配区、质检线装配区等主要作业区域，并为AGV小车等留置专门的充电区和行走通道。其中，各个装配作业区根据装配流程设计了对应数量的作业工位供机械手进行自动组装。根据调研情况，主要为CW公司设计了U 型和S 型两种初步布局方案，分别如图2和图3所示。

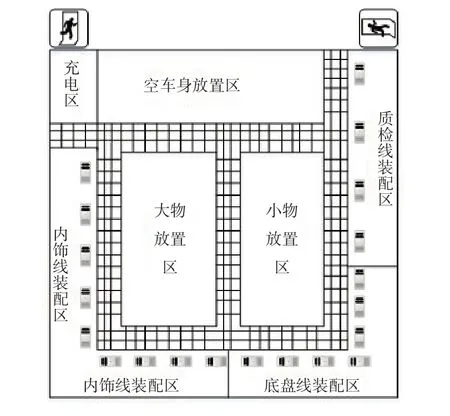
图2 U型布局设计

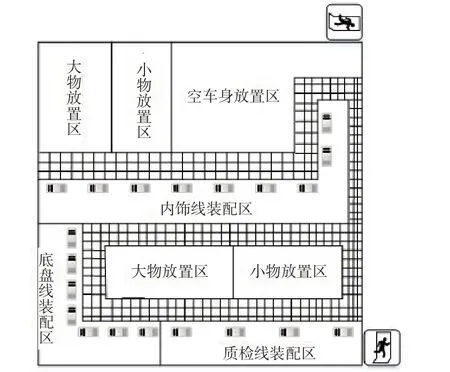
图3 S型布局设计

3.2 Petri网与FlexSim映射规则

层次Petri网是一种静态仿真模型，不能实现模型的动态仿真和分析，因此需要运用FlexSim 软件在静态分析的基础上，根据两个软件之间的映射规则建立动态仿真模型，映射规则为：

（1）层次Petri网中常用的表示状态或场所的库所可以对应FlexSim 中的发生器、吸收器、暂存区、货架等实体。

（2）层次Petri网中常用的表示事件或活动的变迁可以对应FlexSim 中的处理器、分解器、合成器、机器人等实体。

（3）层次Petri网中有向弧与FlexSim 中的连接方式A对应，表示产品或者信息的流转方向。为了实现工序间的流转，还可以借助FlexSim中的传送带、机器人、叉车等运输工具。

3.3 FlexSim建模仿真

以装配100台纯电动车为研究对象，将所需要的大物原材料、小物原材料、空车身等通过BOM（物料清单）的统计情况分别经发生器按照时间间隔1s源源不断的产生，以满足装配线的正常运行。每道安装工序机械手的操作时间通过预定时间标准法测算，并根据现有情况安排的机械手数量通过任务分配器调用。根据装配车间的面积实际数据，通过网络节点类的实体进行仿真，设定各区域的具体位置和AGV的运行路线。

此外，设定AGV初始位置在充电区，AGV机器人最大速度2m/s，加速1m/s，减速1m/s。物料暂存区的货架容量为10 000 000件。

4 基于TOPSIS法的仿真布局结果分析

4.1 TOPSIS法选择

根据两种布局方案分别运行模型，得到平均堵塞时间、平均加工时间、平均闲置时间等主要数据。同时对CW公司的专家组调研，赋予3组数据不同的权重，见表2。

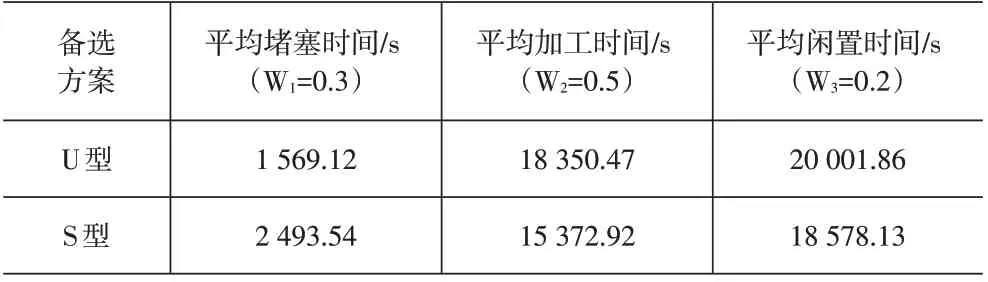
表2 两种布局方案的数据及权重

TOPSIS法又称为理想解法，能充分利用原始数据的信息，精确地反映各评价方案之间的差距，适用于解决多指标问题。该公司的两个布局方案有多个指标需要衡量，可以借助TOPSIS法找到接近正理想解，远离负理想解的最优方案。

4.2 具体分析

（1）用向量规范法求解规范化矩阵b

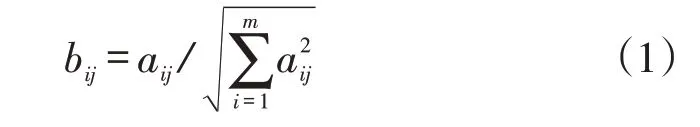
根据式（1）对表2中的数据进行规范化处理，得到结果见表3。

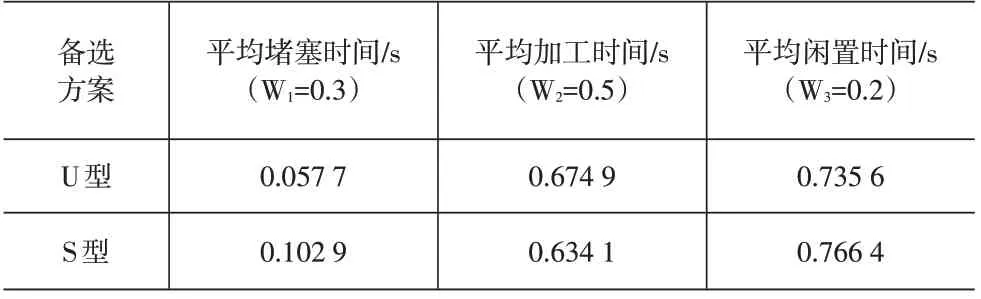
表3 规范化数据以及权重

（2）构造加权规范矩阵X。

根据式（2）可得矩阵X：

（3）确定正理想解和负理想解

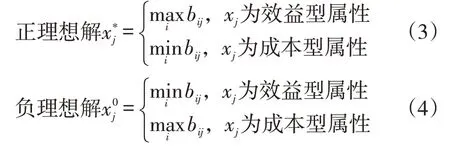
根据式（3）和式（4）可得理想解X*和负理想解X。

（4）计算各方案到正理想解与负理想解距离

各方案到正理想解的距离为：

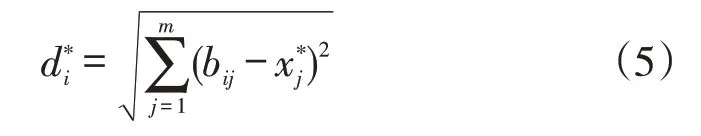
各方案到负理想解的距离为：

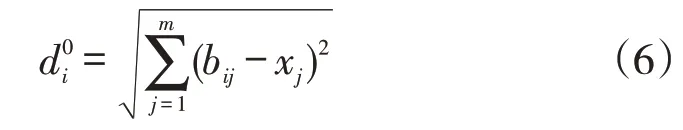
（5）确定两个方案的综合评价指数

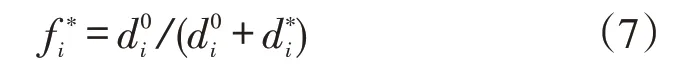
根据式（5）-式（7）得到两个方案到正理想解和负理想解的距离，见表4。

表4 距离数据

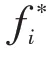
5 结语

为了解决CW公司的绿色汽车装配线布局规划问题，本文首先根据公司运作的现状，尤其是纯电动车装配生产流程，划分出作业单元模块，运用Petri网构建静态模型，根据Petri网与FlexSim的映射规则，将静态模型转化为动态可视化仿真模型，对CW公司拟采用的U型和S型两种布局方式进行仿真建模分析，得出相应的运行数据。进而采用TOPSIS方法对平均堵塞时间、平均加工时间、平均闲置时间三项重要数据进行分析，得出了最适合CW公司现状的为U型布局方式。但是，本文在研究装配线布局问题时主要考虑装配作业流程，尚未把装配线的节拍、装配线的设备数量优化等问题考虑在内，缺乏系统性的规划，如何运用系统论的思想解决绿色汽车装配线一体化问题，具有更强的现实意义和应用价值，是后续研究的主要方向。