基于EMD-SARIMA模型的铁路商品汽车运量预测

张旭宁

（中铁特货物流股份有限公司 北京分公司，北京 100071）

0 引言

在我国汽车产业快速转型升级，高质量发展的背景下，我国商品汽车物流发展空间巨大，加之国家运输结构调整和绿色物流发展政策的实施，促进了商品汽车运输市场的规范化与公平化，也为铁路商品汽车运输提供了良好的发展机遇。商品汽车运量预测是精准对接商品汽车物流市场需求变化的重要依据，有助于铁路部门针对运量变化情况做出快速响应，不断提升铁路商品汽车物流发展整体水平，从长远来看，对商品汽车物流体系中的节能减排、降低商品汽车物流成本等问题具有重要意义。

铁路商品汽车月度运量数据是时间序列数据，呈现明显的递增趋势和季节波动性，SARIMA模型是一种常用的对含有季节性成分数据进行分析的时间序列模型。铁路商品汽车月度运量采集过程中会受到随机性的影响，数据不可避免地存在一些噪声成分,如果对噪声不加处理而直接分析，很有可能得到的结果与真实的情况存在偏差，对后续的分析工作造成影响。因而，建模前先要对数据进行预处理。本文提出一种基于经验模态分解（EMD）和SARIMA 的组合预测模型，先进行去噪处理，然后对数据进行重构，用重构后的数据建立SARIMA时间序列模型，以提高预测的精准度。

1 模型方法

1.1 经验模态分解

经验模态分解（Empirical Mode Decomposition，EMD）是一种适合于分析非平稳时间序列的方法，它的思想是将数据信号分解为有限个本征模函数（Intrinic Mode Function，IMF），IMF分量包含了原始数据信号不同时间尺度的局部特征信号。由于EMD的基函数是根据数据信号自身所分解得到，所以相较于傅立叶变换、小波分解等方法，EMD更直接、直观，后验以及自适应。所以EMD 方法从1998 年被Huang，等提出之后，经专家学者不断的研究与完善，如今已被广泛应用于各种工程实践中，并取得了良好的效果。

EMD分解得到的结果由若干个本征模函数与一个残差项构成，每个本征模函数需要满足以下两个条件：（1）整个时间历程内，信号中穿越零点的数量与通过极值点的数量应该相等，如果不相等时，其差值不应该为两个或两个以上；（2）在任意一点，局部上下极值包络的均值必须为零。基于上述两个条件，EMD分解算法的具体步骤如下：

1.2 SARIMA模型介绍

对处理时间序列问题而言，ARMA模型是目前最常用的拟合模型，由自回归模型（AR）与移动平均模型（MA）有机组合而成，实质就是由其自身的过去值或滞后值以及随机干扰项来解释模型结构，见式（5）。

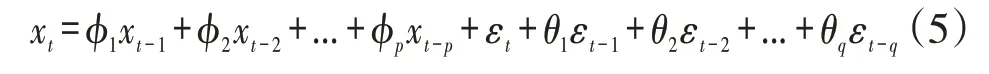
式中：为时间序列中的时刻，x,x,…,x为时间序列数据，，，…，ϕ为自回归系数，，，…，θ为移动平均系数，和分别为自回归项AR的阶数和移动平均项MA阶数，ε为白噪声序列，并且和时刻之前的序列x( )不相关，式（5）可标记为ARMA()模型。

平稳时间序列是ARMA模型的建模前提。当时间序列蕴涵趋势性，可通过差分运算提取趋势信息，这时称该序列为差分平稳序列，对差分平稳序列可以使用ARIMA()模型进行拟合，为简化表述，引入延迟算子，其中x=Bx，模型可表示为：

1.3 EMD-SARIMA模型

EMD-SARIMA模型是把EMD方法和SARIMA模型相结合的一种数据处理方法，先利用EMD将时间序列分解成多个相互独立且相互平稳的分量，再分别对各个分量建立相对应的SARIMA时间序列模型，去除噪声分量，然后进行数据重构，将重构后的数据再进行SARIMA建模及预测，这种基于EMD和SARIMA的组合预测模型，能够克服单一模型的局限性，改善预测精度。

2 实证分析

2.1 数据来源

本文基于铁路商品汽车运输实际数据展开研究，采用2010年1月至2020年6月的全国铁路商品汽车月度运量数据，共计126个数据作为训练集，进行模型构建，使用2020年7月至11月的数据，共计5个数据作为测试集，进行模型检验。同时，本文将通过对比使用SARIMA模型与EMD-SARIMA模型的优劣性，验证是否重构后的EMD-SARIMA模型将比SARIMA模型有着更优的预测效果。

2.2 EMD-SARIMA模型预测

本文使用python的pyhht库中的EMD函数，对商品汽车月度运量数据分解之后得到3个IMF分量与1个res 残差项，分解结果如图1 所示，图中的Signal 为原始数据。

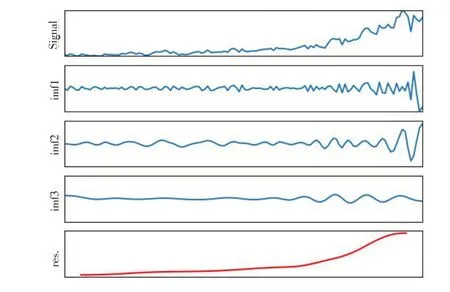
图1 商品汽车月度运量时间序列EMD分解图

图1中的本征模函数按照频率由高至低的顺序排序，分别展示了商品汽车月度运量在2010 年1 月至2020年6月这一段时间内的不同频率与振幅，说明了铁路商品汽车月度运量由3个周期变化的影响因素复合而来，趋势项表明月度运量呈递增趋势。每一个本征模函数都具有一定的物理意义或经济意义。

对商品汽车运量进行EMD分解之后，将分别对分解后的IMF分量与残差项进行白噪声检验，得到检验结果发现IMF1分量为一个白噪声序列，IMF2、IMF3与res分量不是白噪声序列。因此，本文将分别对IMF2、IMF3与res进行SARIMA建模，并使用SARIMA模型对训练期的数据进行预测，预测结果如图2-图4所示。

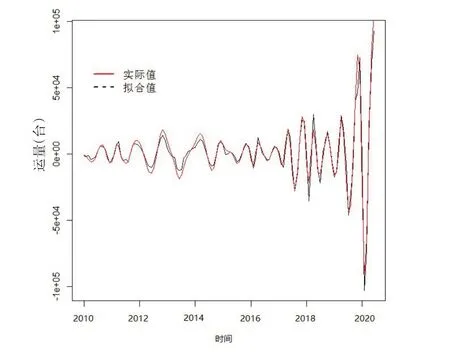
图2 IMF2分量拟合值与实际值

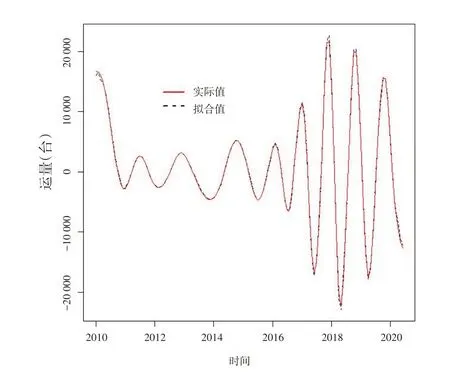
图3 IMF3分量拟合值与实际值

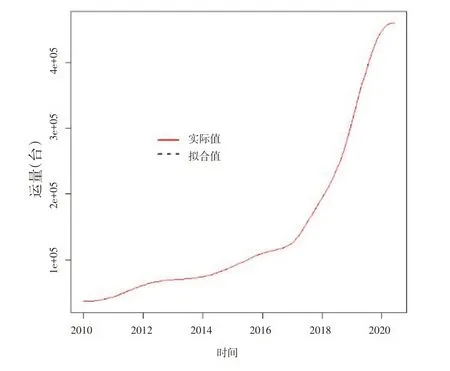
图4 res分量拟合值与实际值

从图2-图4中可以看出每个分量预测结果较好地重现了周期特征和趋势特征，并且随着IMF阶数的增加，亦即各分量震荡频率的降低，预测精度逐渐增大。

将原始的IMF1分量与预测的IMF2、IMF3、res分量相加，得到重构后的数据用于SARIMA 模型建模。使用R软件进行了超参数搜索，得到具有最优效果的模型为SARIMA(2,1,0)(1,0,0)[12]。经过对参数进行估计，得出各个参数的估计值，见表1。

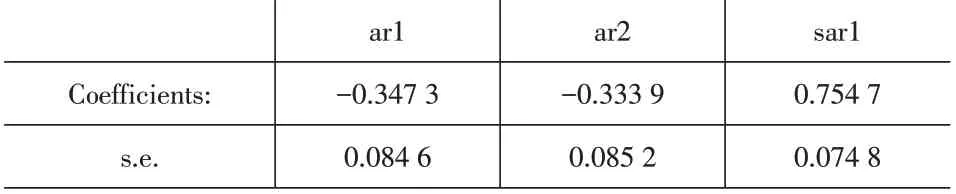
表1 重构后数据的SARIMA(2,1,0)(1,0,0)[12]模型参数

采用2020年7月至2020年11月的数据进行模型检验，使用建立的模型进行预测，预测值与真实值的误差见表2，并绘制预测图，如图5所示。

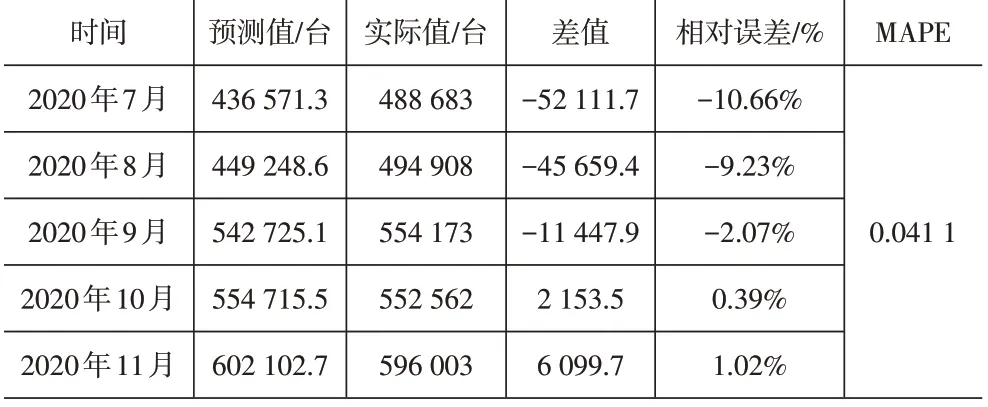
表2 重构后数据的SARIMA模型预测结果误差

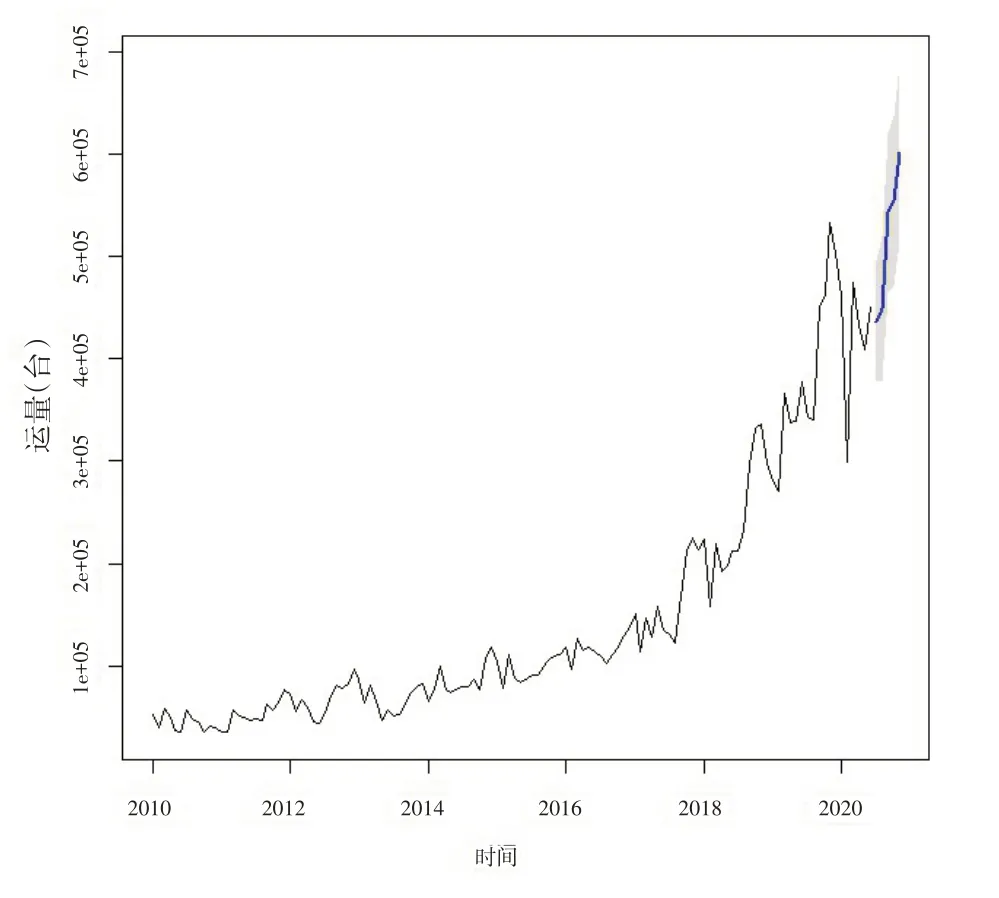
图5 重构后数据的预测结果

采用平均绝对百分误差（MAPE）对预测效果进行评价，其计算公式如下：

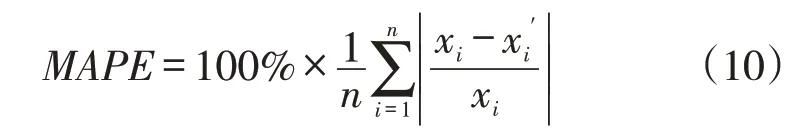
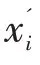
由表2、图5可知，使用重构后数据建立的SARIMA模型可以较好的预测出铁路商品车运量的变化趋势，在后续5个月中预测值的MAPE达到了4.11%，有着很高的预测精度。

2.3 性能比较

为了检验直接使用SARIMA 模型与使用EMDSARIMA模型哪一个具有更优的效果。本文直接使用SARIMA模型进行模型的构建，建模方法与前文相同，得到模型SARIMA(1,1,1)(1,0,2)[12]，同样使用2020 年7月至2020年11月的数据对建立的模型进行适用性检验。模型的预测值与原始数据的真实值误差见表3。

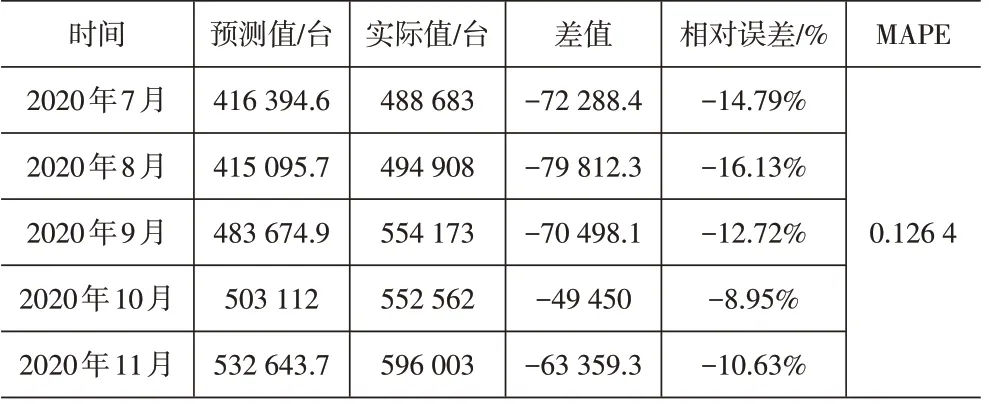
表3 原始数据的SARIMA模型预测结果误差

比较EMD-SARIMA与经典SARIMA模型预测误差，结果见表4。

表4 两种模型的预测误差

从表4可以看出，就短期预测而言，EMD-SARIMA模型预测精度比单一SARIMA模型预测精度提升较大。该模型如果应用于实际生产将能较为准确的预测未来月份的运量值，能够为铁路商品汽车运输相关工作提供一定的决策依据。

3 结语

（1）结合EMD方法建立了一种新的SARIMA时间序列预测模型，用来实现铁路商品汽车月度运量预测。为了比较EMD-SARIMA模型与SARIMA的预测性能，使用2020年7月至11月的数据对建立的模型进行了模型预测效果检验，检验结果显示：EMD-SARIMA预测模型在2020年7月至2020年11月的平均绝对百分比误差（MAPE）可以到达0.041 1，而单一使用SARIMA模型的MAPE值为0.126 4，EMD-SARIMA模型预测效果优于SARIMA 模型。本文建立的EMDSARIMA模型有着很高的预测精度，能够学习获取时间序列铁路商品汽车月度运量的成长过程及发展趋势，挖掘其季节性波动规律，是一种可靠的时间序列预测方法，在铁路商品汽车月度运量时间序列的短期预测方面有较优的性能。

（2）通过研究铁路商品汽车运量预测的方法，得到更为精准的运量预测模型，用以提前研判未来短期内铁路商品汽车运输市场需求，为解决铁路商品汽车物流高质量发展过程中面临的问题起到重要参考作用。一是为准备和调配短期铁路运力打下基础，有助于合理安排运输车数量，及时备用和解备，缓解阶段性JSQ型空车紧张的局面，同时可以降低各铁路局集团公司的“中停时”指标。二是通过预测淡旺季运量，合理安排JSQ型车的检修计划，做好淡季多修车，旺季尽量不修车，缓解装备检修能力不足的问题。三是有助于提高铁路商品汽车运输网络的集疏能力，根据各主要场站的接卸能力并结合高峰期的运量预测，可以提前选好辅助卸车点，租赁临时仓储场地，同时配送企业也可提前调拨作业板车、安排作业人员，从容应对运量变化带来的作业压力，确保装得上、卸得下、驳得出。四是有助于跟运量挂钩的流动资金、预算、工作量等指标的合理安排。

本文不足之处是建立的EMD-SARIMA模型仅使用了铁路商品汽车历史运量数据来预测未来的运量，未研究相关因素对于运量的影响机理，在影响运量的相关因素研究方面还存在欠缺。