基于小波分解的AVOA-DELM月径流时间序列预测模型及应用
张亚杰
(云南省玉溪市易门县水利局,云南 玉溪 651100)
径流时间序列预测是指依据已有的历史监测数据,通过科学的方法推测将来的径流变化趋势。提高径流时间序列预测精度对区域水资源开发利用、防洪抗旱规划、水库优化调度等具有重要意义。传统中长期径流预测模型有回归类模型[1]、集对分析模型[2]和灰色模型[3-4]等,这类模型原理简单、速度快,但由于径流受气候变化、人类活动、土地利用变化和植被覆盖等多种因素的影响,径流序列呈现出非平稳性和多尺度等特征,为提高预测精度带来了难度[5]。当前,互补集合经验模态分解(CEEMD)、奇异谱分解(SSA)、变分模态分解(VMD)、极点对称模态分解(ESMD)等分解算法是径流时间预测前处理的常用和有效方法,通过分解算法可将复杂的原始径流序列分解为多个平稳子序列进行预测,可大幅提升模型精度,如桑宇婷等[6]利用互补集合经验模态分解(CEEMD)方法和BP神经网络建立组合预测模型,将其应用于汾河上游月径流预测;王丽丽等[7]融合奇异谱分析(SSA)方法、灰狼优化算法、回归支持向量机模型,提出SSA-GWO-SVR月径流组合预测模型;吕晗芳等[8]建立变分模态分解(VMD)-最小二乘支持向量回归机(LSSVM)耦合模型,将其应用于上静游站等多个水文站月径流预测;李继清等[9]融合极点对称模态分解(ESMD)与BP神经网络,构建ESMD-BP模型对黄河上游唐乃亥站进行径流预报。
分解算法是月径流时间预测前处理的常用方法之一,将复杂的原始月径流序列分解为多个平稳子序列进行预测,可大幅提升模型精度。目前,CEEMD、SSA、VMD等时间序列分解方法已在月径流时序数据分解中得到应用,并取得较好的分解效果;BP、SVM、LSTM等模型是月径流时间序列预测的最常用的模型之一,但BP、SVM、LSTM模型存在缺点与不足,如BP神经网络存在设置参数多、易陷入局部最优等缺点;SVM模型存在对参数敏感、大容量样本预报中表现不佳等不足;LSTM模型预测性能较好,但存在内存资源消耗大、运行时间长等缺陷。小波分解(wavelet decomposition,WD)是以傅里叶变换为数学基础的信号预处理方法,能很好地平衡时间分辨率和频率分辨率之间的矛盾,由于其较好的时序数据分解效果,已在处理各类非平稳信号中得到广泛应用。非洲秃鹫优化算法(african vultures optimization algorithm,AVOA)是Abdollahzadeh B等[12]于2021年受非洲秃鹫觅食和导航行为启发而提出的一种新型元启发式优化算法,具有寻优能力强、收敛速度快等优点。深度极限学习机(deep extreme learning machine,DELM)也叫多层极限学习机,其采用多个基于极限学习机(extreme learning machine,ELM)的自编码器(ELM-AE)进行无监督预训练,然后利用各ELM-AE的输出权重初始化整个DELM,从结构上看DELM相当于把多个ELM连接到一起,但它相对于ELM能更全面地捕捉到数据之间的映射关系并提高处理高维度输入变量的精确度。与传统ELM相比,具有随机参数少,网络复杂度低,激活函数类型多样化等优点[13-15]。但在实际应用中,DELM隐含层神经元数对DELM网络预测性能影响较大,目前主要采用人工试算等方法确定,不但费时繁琐,且精度不高。
为提高月径流时间序列预测精度,进一步拓展径流预测组合模型应用范畴,基于WD方法、AVOA算法和DELM网络,提出WD-AVOA-DELM月径流时间序列组合预测模型,并构建基于支持向量机(SVM)、BP神经网络2种预测器的WD-AVOA-SVM、WD-AVOA-BP、AVOA-DELM、AVOA-SVM、AVOA-BP作分析对比模型,将该6种模型应用于云南省丫勒水文站月径流时间序列预测,旨在验证WD-AVOA-DELM模型用于月径流时间序列预测的可行性。
1 研究方法
1.1 小波分解(WD)
小波分解(WD)基本思想是利用尺度空间Vj和小波空间Wj来表示平方可积函数空间L2(R)。定义{Vj}j∈Z是L2(R)上的一列闭子空间,小波空间Wj是Vj+1与Vj之差,即Vj+1=Vj⊕Wj,则可以推得[10-11]:
(1)
在此基础上,利用Mallat提出的快速小波变换分解方法将非平稳时间序列分解为若干不同尺度下的平稳时间序列:
cj+1=Hcj,dj+1=Gcj,j=0,1,…,J
(2)
式中H——分解低通滤波器;G——分解高通滤波器;J——尺度数;{cj}、{dj}——原始时间序列c0的低频、高频成分。
1.2 非洲秃鹫优化算法(AVOA)
AVOA是受非洲秃鹫觅食和导航行为启发提出的一种元启发式优化算法。AVOA数学描述如下[12]。
a)确定最佳秃鹫。AVOA通过计算种群所有秃鹫适应度,选择最优和次优适应度对应的秃鹫作为最优秃鹫和次优秃鹫位置,其他秃鹫利用式(3)向最优和次优秃鹫移动。
(3)
式中Ri(t)——除最优、次优秃鹫外的其他秃鹫位置;BestV1、BestV2——最优秃鹫和次优秃鹫位置;L1、L2——介于0和1之间待测量参数,其和为1;pi——选择最佳秃鹫的概率;fi——其他秃鹫适应度;t——当前迭代次数;其他参数意义同上。
b)秃鹫饱食率。秃鹫经常觅食,若它们处于饱食状态,则拥有较高能量,这使得它们可以在更广阔的区域觅食;若处于饥饿状态,则没有足够的能量飞行和在更强壮的秃鹰附近觅食。饱食率数学描述为:
(4)
式中F——秃鹫饱食率;T——最大迭代次数;z——-1和1之间的随机数;h——-2和2之间的随机数;rand1——0和1之间的随机数;w——控制勘探过程参数,随着w值增大,算法进入勘探阶段的概率增大,反知概率减小。
c)探索阶段。秃鹫具有很高的视觉能力和较好的觅食能力。在AVOA中,秃鹫通过式(5)随机搜寻不同区域。
(5)
式中Pi(t+1)——第t+1次迭代秃鹫位置;Pi(t)——第t次迭代秃鹫位置;X——秃鹫随机移动的地方,以保护食物免受其他秃鹫夺取,X=2×rand,rand表示0和1之间的随机数;P1——探索阶段选择参数;rand2、rand3、randP1——0和1之间的随机数;ub、lb——搜索空间上、下限值;其他参数意义同上。
d)开发阶段。AVOA中,开发阶段分为开发一阶段和开发二阶段2种策略,并通过开发阶段选择参数P2、P3决定采用何种策略进行位置更新。开发第一阶段秃鹫位置更新描述如下:
Pi(t+1)=

(6)
式中 rand4、rand5、rand6、randP2——0和1之间的随机数;P2——开发第一阶段更新策略选择参数;其他参数意义同上。
开发第二阶段秃鹫位置更新描述如下:
(7)
式中 BestV1(t)、BestV2(t)——第t次迭代最优、次优秃鹫位置;randP3——0和1之间的随机数;P3——开发第二阶段更新策略选择参数;Levy(d)——随即游走,其每一步方向完全随机而各向同性,步长为重尾分布;其他参数意义同上。
1.3 深度极限学习机(DELM)
深度极限学习机(DELM)从结构上看相当于把多个极限学习机(ELM)连接到一起,能更全面地捕捉到数据之间的映射关系,有效提高处理高维度、非线性数据的能力。
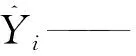
设DELM有Q组训练数据{(xi,yi)|i=1,2,…,Q|}和M个隐含层,将输入训练数据样本根据自编码器极限学习机(ELM-AE)理论得到第一个权值矩阵β1,接着得到隐含层特征向量H1,…,以此类推,能够得到M层的输入层权重矩阵βM和隐含层特征向量HM。DELM数学模型表述式为[16-18]:
(8)

1.4 WD-AVOA-DELM建模流程
步骤一采用deny小波作为WD的基函数,将丫勒水文站1990年1月至2009年12月共240个月月径流时序数据分解为4个子序列分量S1—S4,见图1。从图1可以看出,S1幅值最大,聚集了原始月径流时序数据的大部分能量,描述了径流序列的趋势。S4为所有分解分量中的最高频成分,也是幅值最低的分量,描述了原始月径流时序数据的波动情况。

图1 丫勒站月径流时序WD分解结果
步骤二在延迟时间为1的条件下,采用虚假最邻近法(FNN)确定各子序列分量及原序列的嵌入维度m,即利用序列前m个月径流预测当月月径流量。本文大致按2∶1划分训练、预测样本,即利用实例1~156个月月径流数据作为训练样本,157~240月径流数据作为预测样本。
步骤三选用3隐层DELM网络。针对各子序列分量,通过AVOA优化各隐含层神经元数,构建WD-AVOA-DELM模型目标函数:

(9)
步骤四设置AVOA种群规模N,最大迭代次数T,各阶段更新策略选择参数P1、P2、P3;随机初始化秃鹫种群位置Pi(i=1,2,…,N),令当前迭代次数t=0。
步骤五计算所有秃鹫适应度值,确定最优、次优秃鹫位置BestV1、BestV2。
步骤六对于种群所有秃鹫,利用式(3)其他秃鹫位置;利用式(4)计算秃鹫饱食率,若|F|≥1,利用式(5)更新秃鹫位置;若0.5≤|F|< 1,利用式(6)更新秃鹫位置;若0≤|F|< 0.5,利用式(7)更新秃鹫位置。
步骤七计算更新后所有秃鹫种适应度,比较并确定最优、次优秃鹫位置BestV1、BestV2。
步骤八令t=t+1。判断是否满足终止条件,若是,输出BestV1,算法结束;否则转至步骤六。
步骤九输出BestV1,即DELM最佳隐含层神经元数。利用AVOA-DELM模型对各子序列分量S1—S4进行预测,预测结果叠加重构后即得到丫勒站最终月径流预测结果。
2 实例应用
丫勒水文站位于云南玉溪市峨山县,建于1958年12月,1975年撤销,1990年恢复,属绿汁江干流控制站,控制径流面积7 098 km2,为国家重要水文站及省级报汛站。绿汁江发源于楚雄州武定县猫街镇干沙沟西麓,为元江右岸一级支流,属红河水系。绿汁江由北向南流经禄丰、双柏、易门、峨山、新平等县后汇入元江,径流面积8 613 km2,河流长294 km,自然落差1 651 m,平均比降4.9‰,流域水力资源理论蕴藏量为330.7 MW。本文数据来源于云南省丫勒水文站1990年1月至2009年12月共240个实测月径流序列。从图2可以看出,丫勒水文站月径流时序数据呈现出典型的多尺度、非线性特征。

图2 1990—2009年丫勒水文站月径流变化曲线
2.1 参数设置
WD-AVOA-DELM、WD-AVOA-SVM、WD-AVOA-BP、AVOA-DELM、AVOA-SVM、AVOA-BP模型参数设置见表1。

表1 各模型参数设置
2.2 预测结果及分析
利用所构建的6种模型对实例月径流进行预测,结果见表2,预测结果见图3、4。利用平均相对误差(MAPE)、平均绝对误差(MAE)、确定性系数(DC)、合格率(QR)对各模型进行评估,见式(10)。
(10)
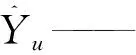
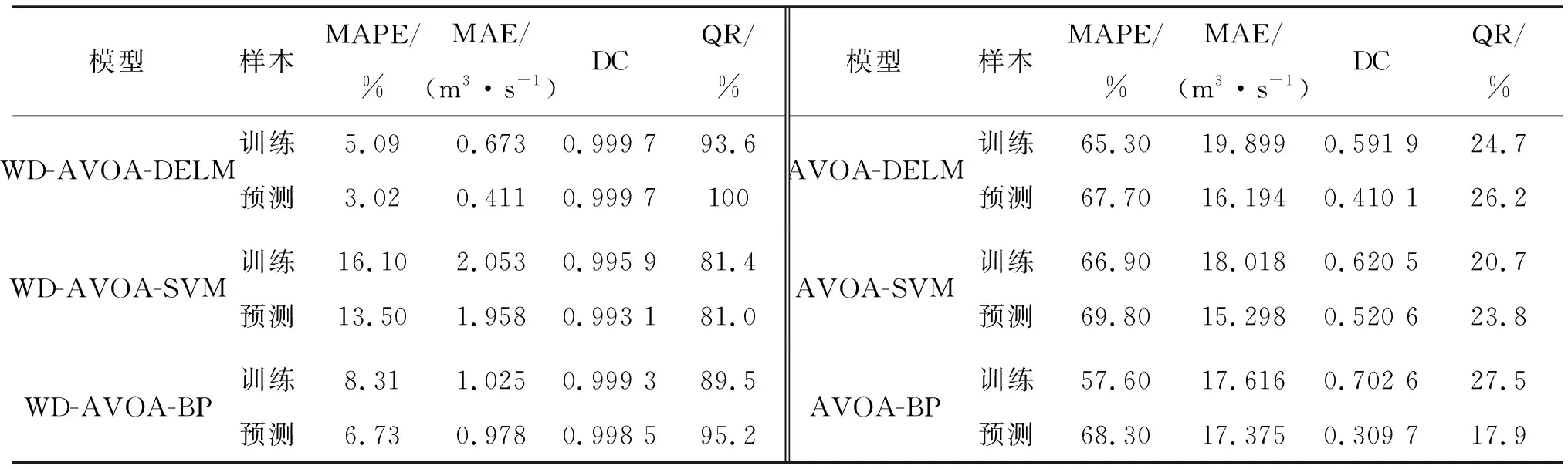
表2 丫勒月径流时间序列训练、预测结果对比
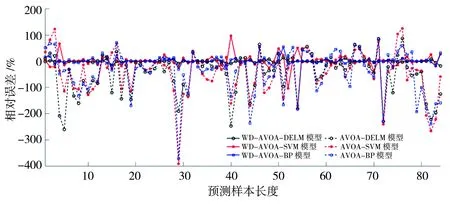
图3 丫勒站月径流时间序列预测相对误差
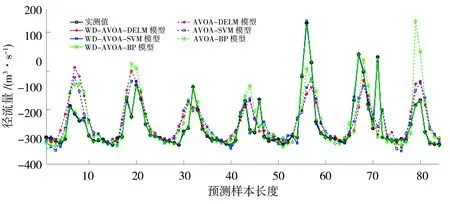
图4 丫勒站月径流时间序列预测效果
依据表2及图3、4可以得出以下结论。
a)WD-AVOA-DELM模型对丫勒站预测的MAPE、MAE分别为3.02%、0.411 m3/s,预测误差较WD-AVOA-SVM、WD-AVOA-BP模型降低55.1%以上,预测精度较AVOA-DELM、AVOA-SVM、AVOA-BP模型提高1个数量级以上,QR为100%,DC达0.999 7,模型精度评价等级为甲级(合格率大于等于85%、确定性系数大于等于0.90)。可见,WD-AVOA-DELM模型具有更好的预测精度,将其用于月径流时间序列预测是可行的。
b)从表2来看,经WD方法分解处理的WD-AVOA-DELM、WD-AVOA-SVM、WD-AVOA-BP模型预测精度远远优于未经分解处理的AVOA-DELM、AVOA-SVM、AVOA-BP模型,可见,采用WD对月径流时间序列进行分解,可达到弱化复杂环境对径流时间序列影响的目的,从而提高模型预测精度。
c)依据GB/T 22482—2008《水文情报预报规范》,WD-AVOA-DELM、WD-AVOA-BP模型达到预测精度等级甲级;WD-AVOA-SVM模型达到预测精度等级乙级;AVOA-DELM、AVOA-SVM、AVOA-BP模型预测合格率低于30%,已不能满足径流预测精度需求。WD-AVOA-SVM模型仅达到预测精度等级乙级,预测精度低于WD-AVOA-BP模型,表明SVM模型虽然在小样本预测中具有优势,但在相对大容量样本的月径流中长期预测中不具优势。
d)从图4来看,WD-AVOA-DELM模型预测的绝大多数月径流相对误差在-5%~5%范围内波动,具有较小的预测误差;从图5来看,WD-AVOA-DELM模型预测结果能够很好地逼近实测径流,具有较好的预测效果。通过AVOA优化DELM隐含层神经元数,有效提高了DELM网络的预测精度和智能优水平。
3 结论
为提高月径流时间序列预报精度,提出WD-AVOA-DELM月径流时间序列预测模型,并构建WD-AVOA-SVM、WD-AVOA-BP、AVOA-DELM、AVOA-SVM、AVOA-BP作对比分析模型,通过云南省丫勒站月径流时间序列预测实例对各模型进行检验,得到如下结论。
a)WD-AVOA-DELM模型对丫勒站月径流预测精度远优于WD-AVOA-SVM、WD-AVOA-BP模型,较AVOA-DELM、AVOA-SVM、AVOA-BP模型提高1个数量级以上,预测精度评价等级为甲级,具有较好的预报精度和实际应用价值。
b)采用WD对月径流时间序列进行分解,可将原月径流时间序列分解为更简洁、更具规律的子序列分量,大大降低预测器的预测难度,从而提高预测精度;通过AVOA优化DELM隐含层神经元数,有效提高了DELM网络的预测精度和智能优水平。
c)WD-AVOA-DELM模型能充分发挥WD方法、AVOA算法和DELM网络优势,表现出较好的预测精度和稳定性能。本文提出的预测模型及预测方法可为相关径流时间序列预测研究提供新途径。

