基于EFDC模型的感潮河网地区闸门调度研究
张现国,王慧鹏,黄绵松,郑 蕾*,刘晓芳,3
(1.北京首创生态环保集团股份有限公司,北京 100044;2.北京师范大学水科学研究院,北京 100875;3.中国科学院地理科学与资源研究所,北京 100101)
关键字:感潮河网;EFDC;黑臭水体治理;水动力水质模型
随着中国经济的快速发展,近十几年来水环境问题也逐渐暴露出来,全国范围内水体环境普遍存在不同程度的污染[1]。污染物负荷输入及河道水动力条件不足,导致部分城市河流水体出现黑臭现象。治理黑臭水体可以采用控源截污,内源治理和水动力调控等多种手段。其中水动力调控通过对闸坝、泵站等水工构筑物的控制来改善城市河网中的水动力条件,从而提升河道水体的自净能力,降低水体的污染程度,是一种简单高效的方法[2]。本项研究区位于福州感潮河网地区,相比于其他地区城市河流存在着天然的潮汐自然资源优势,更适合使用水动力调控进行水体治理。潮汐具备强大的动能,不仅可以纳潮引水,同时可以将部分污水排出城市河网,对于感潮地区通过潮汐引水治理黑臭水体是一种经济高效的做法,该方法被广泛应用而且切实可行[3]。
感潮河网地区水资源丰富,河网水系复杂,导致如何合理确定水动力调控方案成为能否恢复河道水环境的一个关键问题。而且城市河网承担了景观、行洪排涝、灌溉、纳污等多项功能,不同的场景下需要确定不同的调度方案。因此,需要借助水质模型来快速获取多种情景的结果以辅助水动力调控。EFDC模型是当前广泛使用的三维水环境生态模型,也是美国环保署(EPA)推荐使用的模型之一。它是威廉玛丽大学维吉尼亚海洋科学研究所的John Hamrick等[4]开发的三维地表水水质数学模型,可实现河流、湖泊、水库、湿地系统、河口和海洋等水体的水动力学和水质模拟。陈正侠等[5]使用该模型与WASP模型在潮汐河网地区成功模拟了突发水污染事件。谢森扬等[6]使用该模型成功对岸线地形复杂的九龙江口-厦门湾潮汐潮流和盐度场的时空变化过程进行模拟。刘建波等[7]使用该模型成功对清澜潮汐汊道的海湾水交换时间进行模拟。
研究区为福州仓山龙津阳岐水系。该区域南北两侧均受到潮汐作用的影响。在潮水的顶托作用下,河网中的水流反复震荡,河道底部污染物上浮进入水体形成污染[8]。人为因素的过度干扰,使得河网自然生态功能逐步丧失,河道水体自净能力变差,河流逐渐呈现出黑臭的状态[9]。研究区河网的复杂性及外侧潮汐水位的影响,导致进行水动力调控难度较高。因此本文的主要目的是使用EFDC模型模拟感潮河网地区的水动力调控方案,在保障目标河段水质达标前提下,确定最优的调度方案,减少泵站补水的能源消耗。
1 材料方法
1.1 研究区概况
研究区为仓山龙津阳岐水系,位于福建省福州市南台岛片区的中部,位于东经119°16′35″~119°21′15″,北纬25°58′50″~26°3′17″,见图1。福州属典型的亚热带季风气候,年平均降水量为900~2 100 mm;年平均气温为20~25℃。研究区水系内共有13条河流,河道总长度31.43 km,汇水面积约为25.49 km2。研究区水系北临闽江、南靠乌龙江,两江水位每日随潮汐作用而变化,因此近江河段均修建有水闸,满足维持河道水位,行洪排涝等功能。研究区范围内有解放大桥潮位站(图1),本文中潮位数据均来自于该站。研究区内共涉及菖蒲水闸、江边水闸等15座水闸及白湖亭河一体化闸泵及阳岐泵站2座泵站。

图1 研究区位置
1.2 研究方法
目前,研究区水系黑臭水体的治理已经基本完成,需要长时期内维持水系水质的达标。但是存在强降雨条件下,截流井溢流导致河道水质变差的问题。同时,对于长时期的运维,还需要尽量降低运维成本。水系河道除了要保证水质达标,还需要保证满足汛期河道行洪要求。因此,本次研究的目标主要包括河道水质达标、降低运维成本及满足河道行洪要求。
为了保证整体运维调度的合理性,本研究按照以下方法步骤进行:①对研究区域内闸坝、泵站等可以人为进行调控的设施基础特征进行分析,确定研究区内水系库容、过流能力等基础情况;②选取可以对研究区水动力及水质情况进行分析的物理模型,并收集模型构建及率定验证所需的相关资料;③根据研究区水系运维的不同目标,设定了晴天汛期、雨天汛期、晴天非汛期、雨天非汛期4种工况,并通过模型模拟不同调度规则下河道内水动力及水质的变化情况;④依据考核目标,分别评价不同调度规则的水质改善维持效果、运维经济成本及水质达标情况,确定最优的调度方案。
1.3 EFDC模型
EFDC模型是开源的三维水质模型,是美国最大日负荷总量(TMDL)计划工具箱中的重要模拟软件。模型内部分为多个相互耦合较为紧密的模块,可以实现包括水动力、温度、沉积物、波浪、有毒物质及水质等不同内容的模拟[10]。水动力模块是模型基础,在模拟过程中首先对水体水动力进行计算,其次对其他模块进行模拟。
EFDC模型水平上采用正交曲线网格或者笛卡尔坐标网格,垂向上采用σ坐标网格。水动力控制方程主要遵循的守恒律包括:质量守恒、能量守恒、动量守恒。水动力模块有3个主要的假设:Boussinesq近似假设,认为水密度不随压力而变化;静水压近似,认为水平尺度远大于垂直尺度,垂向加速度近似为零;准3D近似,在垂向上采用分层求解,避免了完全求解三维Navier-Stokes方程。EFDC动量方程、连续方程及状态方程为[11]:
∂t(mHu)+∂x(myHuu)+∂y(mxHvu)+∂z(mwu)-(mf+v∂xmy-u∂ymx)Hv=-myH∂x(gζ+p)-
my(∂xh-z∂xH)∂zp+∂z(mH-1AV∂zu)+Qu
(1)
∂t(mHu)+∂x(myHuv)+∂y(mxHvv)+∂z(mmv)+(mf+v∂xmy-u∂ymx)Hu=-mxH∂y(gζ+p)-mx(∂yh-z∂yH)∂zp+∂z(mH-1Av∂zv)+Qv
(2)
∂zp=-gH(ρ-ρ0)ρ0-1=-gHb
(3)
∂t(mζ)+∂x(myHu)+∂y(mxHv)+∂z(mw)=0
(4)

(5)
ρ=ρ(p,S,T)
(6)
∂t(mHS)+∂x(myHuS)+∂y(mxHvS)+
∂z(mwS)=∂z(mH-1Ab∂zS)+QS
(7)
∂t(mHT)+∂x(myHuT)+∂y(mxHvT)+
∂z(mwT)=∂z(mH-1Ab∂zT)+QT
(8)
式中u、v、w——边界拟合正交曲线坐标x、y、z方向上的速度分量;mx、my——度量张量的对角分量的平方根;m=mxmy为度量张量行列式的平方根;Av——垂向紊动黏滞系数;Qu、Qv——动量源汇项;p——压力;S——密度;T——温度;H——总水头;QS、QT——盐度、温度的源汇项。
2 模型构建及率定验证
2.1 EFDC模型构建
网格划分是EFDC模型运行的基础,在考虑到时间成本的情况下,模型网格数量越多,模型运行得到的精度越高。研究区河道平均水深为2 m,采用二维正交曲线网格对研究区河道进行概化,最终得到2 503个网格,网格水体区域共143.11 hm2,网格平均DX190.16 m,DY 26.94 m,网格正交误差为2.971°。
模型的主要边界条件为水位开边界,主要分布于靠近南北两侧的水闸处。模型的率定及验证期采用对应日期内的实测潮汐水位。对应的不同工况下的边界条件为汛期及非汛期典型潮位。闽江口为强潮陆相口,潮型为规则半日潮,潮汐一天有2个周期,12 h 50 min为一周期,涨潮约5 h,落潮7.25 h,潮汐特征表见表1。根据解放大桥历史潮位数据,分别选取非汛期及汛期典型潮位,见图2。该研究区内的主要潮汐边界条件均由闸泵进行控制,共概化13处闸门、5处涵管和2处引水泵站。2处引水泵站分别位于阳岐河南侧及白湖亭河南侧,均可以向河道提供4 m3/s的流量。闸门的启闭规则主要根据不同工况下的目标来设定。

表1 解放大桥潮汐特征

图2 解放大桥非汛期及汛期典型潮位
河床糙率是水动力模型构建过程中的一个重要参数,是反映河道对水流阻力影响的一个综合性无量纲数。通过模型率定确定河道整体糙率为0.035。模型时间步长选用动态时间步长,最大动态时间步长为0.15 s。
气象数据来源为中国气象数据网(http://data.cma.cn/),包括气温、降雨、气压、风速、风向、湿度和日照时数,数据的时间间隔为一小时。太阳辐射数据采用日照时数进行计算,具体的计算公式见童成立等[12]研究。
2.2 模型率定验证
为确保建立的模型能够反映研究区的水动力及水质特点,基于实测数据对模型进行率定验证,时期为2017年7月28日至2017年8月4日。在此期间,闸门及泵站的启闭条件设定主要依据为现场闸站运行记录表,将对应的闸站启闭规则概化为时间序列条件输入到模型中。水动力模拟结果选用2017年7月28日9:00—16:00实测数据,模拟结果见图3。从图中可以看出,水动力模拟结果良好,反映出了河道内水位变化的趋势。在监测点LJYZ1和监测点BYT1,水位模拟相对误差分别为8.26%和1.70%,均小于10%。处于河网中心区域的BYT1监测点变化幅度较小,且水位峰值出现时间相对于离外江更近的LJYZ1处有所推后。

图3 2017年7月28日水位模拟结果
每天对整个研究区范围内水质指标进行检测,监测点位置分布见图1。溶解氧和氨氮是环境水体污染的一项重要指标,可以用于衡量水生系统能否维持平衡。此外,溶解氧和氨氮也是城市黑臭水体分级的评价指标之一。因此本次对模型的验证采用的指标主要为溶解氧和氨氮,模拟结果见图4、5。BHT3及LJYZ1监测点处的DO的相对误差分别为16.99%、19.61%,氨氮的相对误差分别为20.32%、28.15%,模型基本上可以反映出水体溶解氧和氨氮的变化趋势。
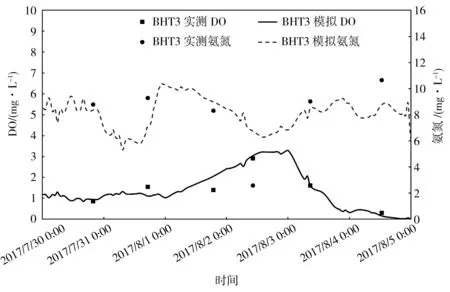
图4 BHT3水质模拟结果

图5 LJYZ1水质模拟结果
3 结果
3.1 模型设定
基于率定验证完成的模型,以图2中非汛期及汛期潮位为基础边界条件,模拟连续4 d采用设定的运维调度规则情况时,研究区内水体水质不同目标下的恢复情况。对于河网水系的运维调度,需要考虑到非汛期及汛期河道行洪的需求,因此在汛期维持河道处于较低水位保证行洪,在非汛期适当维持较高水位保证水质。结合研究区特点,采用南引北排方案:外江水位处于高潮时,利用南部的阳岐闸泵、白湖亭闸泵引水;外江水位处于低潮时,利用北部的龙津一支河水闸及龙津河水闸排水,实现整个研究区内水流从南到北的单向流动。
调度的水质目标主要是氨氮浓度,并以此将水体分为4种情况:不合格(≥8 mg/L)、合格(<8 mg/L)、良好(<6 mg/L)、优秀(<4 mg/L)。不溢流情况下水质必须达标,并尽量维持优秀;溢流情况下需要在72 h内将水质恢复合格。
3.2 模拟结果
非汛期不溢流工况下,分别对不同的引水方式、补水闸泵及水质目标进行了模拟,以期获取最经济及高效的水质恢复调度方式。
当采用潮差及2个泵站同时打开引水时,水质恢复最不利的河段均为半洋亭河,见表2。半洋亭河位于整个潮汐河网的中心区域,相对于其他河道,距离补水及排水闸门都很远。当同时采用研究区南侧阳岐河及白湖亭河进行补水时,由于阳岐河及白湖亭河各自河道的高程、河宽等特征不同,补水在半洋亭河两端形成顶托作用,导致半洋亭河流向反复,见图6,短时间内河道内污染物无法排出河道。

图6 非汛期不溢流采用潮差引水工况下半洋亭河流速和流向(流向相对于模型方向)
非汛期不溢流工况下,主要考虑水质由合格恢复到良好、良好恢复到优秀的过程。采用不同的引水方式及开启不同的闸坝可以得到不同的效果。对于潮差引水方式,研究区内水体从合格恢复到良好的时间花费最多,但引用水量最少,充分利用潮汐进行补水是最为经济的一种方式。但是由于采用潮汐在短时间内换水水量有限,无法使得研究区内水体快速恢复优秀。对于泵站引水方式合格到良好的水质目标下,同时开启2个泵站所需恢复时间最短,但是引水水量也最多,相比于单采用白湖亭河及阳岐河泵站分别多引35.5%、51.4%;单采用白湖亭河泵站所需时间和水量相比其他方式都处于中等水平;单采用阳岐河泵站所用水量最少,但是恢复时间也是泵站引水中相对最长的。综合考虑到泵站开启后需要消耗能源的经济成本及水体水质恢复效果情况,溢流情况下应采用白湖亭泵站恢复河道水质,并在不发生溢流的情况下采用潮差引水来维持河道内水质为良好。
汛期工况和非汛期工况类似,但是由于整个研究区内河道需保持较低水位,在不溢流情况下采用潮差引水时,短时间内河道可换水量不足,从而导致在4 d模拟周期内水质无法从合格恢复到良好。整体而言,汛期情况各种方式下,水质恢复时间要长于非汛期。综合考虑到经济、防汛和水质恢复效果,在汛期应采用白湖亭河泵站进行水质恢复及维系。
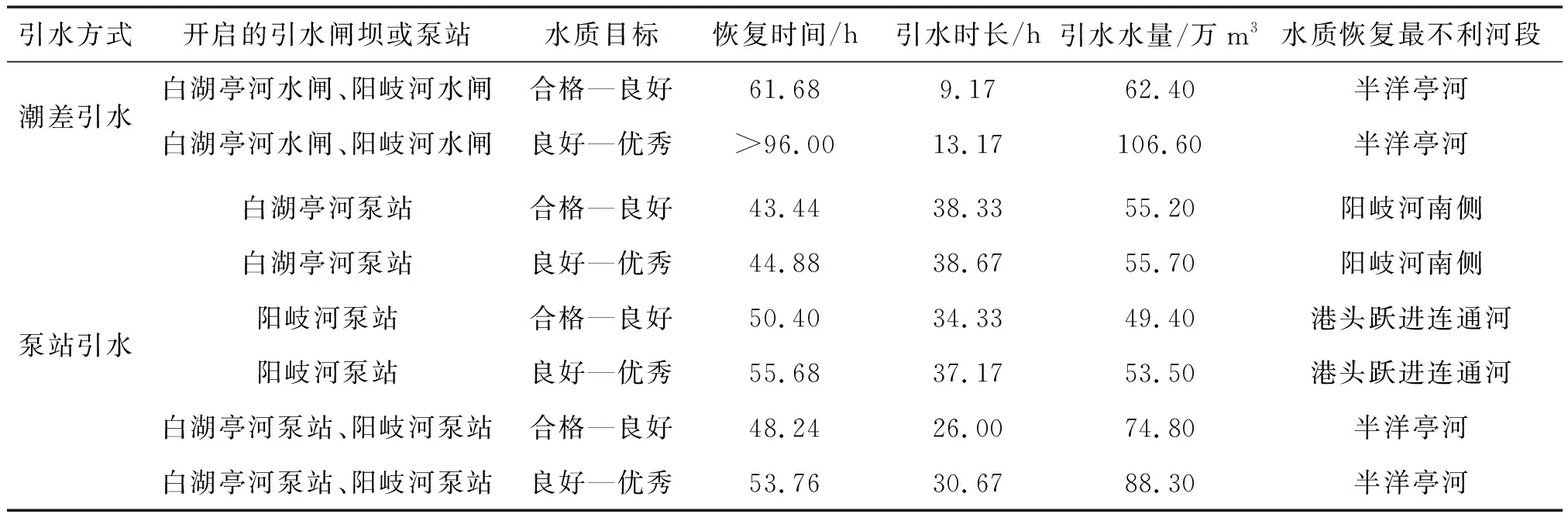
表2 非汛期不溢流工况下模拟结果

表3 非汛期溢流工况下模拟结果

表4 汛期不溢流工况下模拟结果

表5 汛期溢流工况下模拟结果
4 讨论
感潮河网地区水系一般较为复杂,根据与潮汐补水口的距离远近不同,水动力及水质条件均不相同。一般而言,外江水质要明显优于河网内部水质。而且靠近外江的区域水动力条件也优于河网内部[13]。这就导致了河网中心区域的水动力条件及水质状况相对较差。因此,采用水动力调控时,应尽量避免使用双向闸门或泵站进行引水,以免造成河道内部的水流流向反复,水体震荡对河道水质造成负面影响。采用泵站引水,是一种改善河道水质的高效方法,对于非汛期不溢流,水质从合格到良好,白湖亭河泵站、阳岐河泵站和同时开启2个泵站比潮差引水的恢复时间分别缩短29.6%、18.3%和21.8%,而且某些工况下必须采用泵站引水才可以使水体保持优秀目标。但是值得注意的是,采用泵站补水需要确保有效补水,从合格到良好,采用白湖亭河泵站、阳岐河泵站和同时开启2个泵站分别补水74.8万、49.4万、55.2万m3,开启单侧泵站恢复时间均大于同时开启两侧泵站,因此保持河道内水流流向稳定,对水质恢复及维系效果最佳[14]。
模型作为一种辅助手段,可以对复杂河网地区的水系治理及运维起到一定的指导作用[15]。使用模型对污染物溢流及一些突发水体污染事件进行提前模拟,可以为短时间内满足恢复水质要求提前做出应对措施方案,提升运维水系管理水平。同时,使用EFDC模型可以在短时间内对大量的模拟方案进行模拟,来探寻最优的水动力调控规则。
5 结论
综上,EFDC模型可以模拟复杂的感潮河网地区闸泵的水动力调控,辅助应急方案制定及寻求最优运维策略。采用泵站补水可以快速改善河道内水质,相比于潮差引水,非汛期不溢流工况下,水质从合格到良好恢复时间可以缩短18.3%~29.6%。感潮河网地区应根据水系特点,通过调度使水流流向单一稳定,有利于整体河网的水质恢复及水系运维。

