极值原理的一个应用

梁诗雨 韩 菲 罗小荣

新疆师范大学数学科学学院 新疆乌鲁木齐 830017

若方程解的极值在区域的边界达到，我们称方程对应的算子满足极值原理。椭圆方程中，以Laplace方程为例，利用极值原理，可以得到Laplace方程的狄利克雷边值问题的最大模估计。抛物型方程中，热传导方程满足极值原理，用物理知识简单形象地去理解此原理，即在热传导过程中，若物体内无热源，想要温度趋于平衡，则高温处的热量需输向低温处，这种情况下，物体最高温度必在初始时物体的边界处达到。这是极值原理在现实生活中真实现象的映射[1-2]。兰乃端、常保平应用Hopf极值原理研究了一类具有边界条件的半线性椭圆方程解的梯度q的估计[3]。麻西南、邱国寰等人在研究Hesse方程的Neumann边值问题时，选取较合适的函数，利用极值原理方法给出了所研究问题的解的梯度估计[4]。徐金菊综合利用Lieberman[5]等人的技巧，运用极大值原理证明了平均曲率方程Neumann问题解的边界梯度估化，从而得到一个存在性定理[6-7]。本文应用伯恩斯坦方法，应用极值原理，得出一类线性方程的梯度估计。

1 准备知识

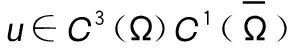
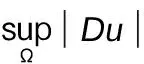
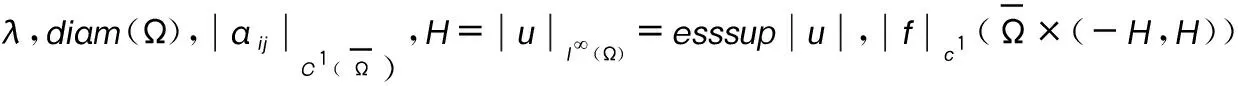
2 主要结果

定理2 设aij(x)Diju+bi(x)Diu=f(x，u，∇u)

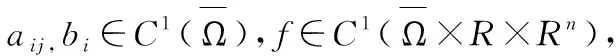
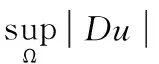
(1)

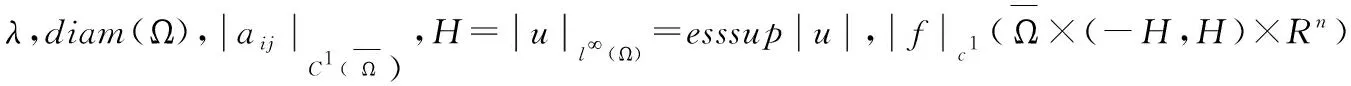
证明：取测值函数P=|Du|2+β|u|2+eαx1，其中α、β待定。

令L=aijDij+biDi先计算L(|Du|2)：

可得：

对aij(x)Diju+bi(x)Diu=f(x，u，∇u)每一项关于xl求导，得：

将上式每一项乘Dlu再对l求和整理：

现对上式等号左边每一项估计：

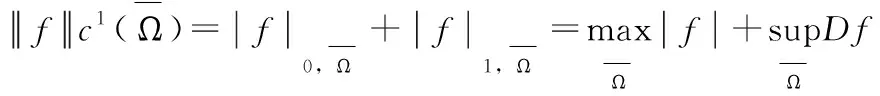
可知：

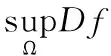
(2)

由:

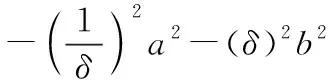
(3)

即：

又：

已知：

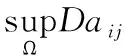
又：

由一致椭圆条件得：

及：

综上可得：

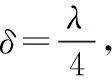
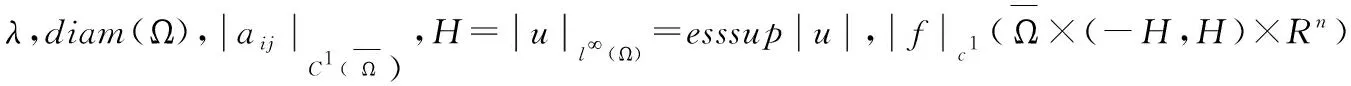
又：

对上式等号右边两项估计后可得：

L(u2)≥2|f|c1|u|+2λ|Du|2≥2λ|Du|2-2|f|c1|u|≥2λ|Du|2-2|f|c1H

综上我们有：

取β足够大，则有：

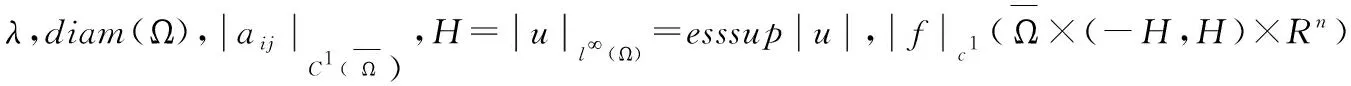
对c4常数项，由于:

L(eαx1)=α11α2eαx1+b1αeαx1

及：

其中x1与diam(Ω)相关，取α足够大，则:

a11α2eαx1+b1αeαx1-C4≥0

则有：

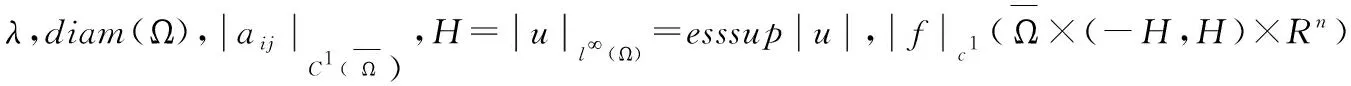
由于L(P)≥0，满足弱极值原理，即：

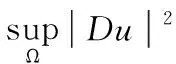
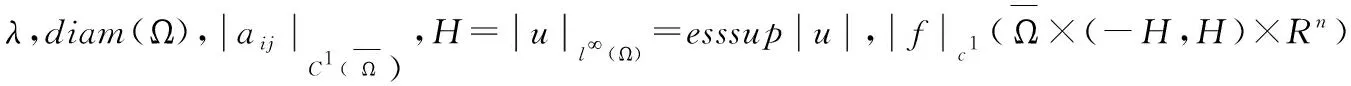
则得到：

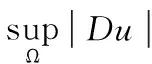
由此(1)式结论成立。