基于势函数的井网流线演变特征

何海峰，徐宏光，曹嫣镔，李健康，郭省学，唐洪涛

（1.中国石化胜利油田分公司孤东采油厂，山东东营 257237；2.中国石化胜利油田分公司石油工程技术研究院，山东东营 257000；3.中国石化胜利石油管理局有限公司博士后科研工作站，山东东营 257000；4.西南石油大学石油与天然气工程学院，四川成都 637000；5.山东省稠油开采技术重点实验室，山东东营 257000；6.中国石化胜利油田分公司胜利采油厂，山东东营 257051）

流线是欧拉法描述流体运动的几何表示，用于研究流体质点在不同空间位置上的运动情况。流线表示出了流场中流体质点瞬时的流动方向，流线与等压线是正交的。流线模拟能够较为真实地反映流体的流动状态，形象、直观地反映注采井的流动耦合关系，用于确定井网的泄油面积，得到油藏中的剩余油富集区。

在国外，流线模拟法最早由MUSKAT 等引入油气藏开发研究中，通过电传导实验获得了面积井网的流线分布［1］。LE BLANC 依据压力叠加原理求解了均质油藏的压力分布，利用流函数得到了井网的流线分布［2］。MARTIN 等采用流线数值模拟法研究流度比对五点井网开发效果的影响［3］。POLLOCK提出了流线追踪法［4］，为流线数值模拟方法的发展奠定了基础。CHARLES 等采用流线模拟，利用欧拉法求解了不同井网组合下的流场分布［5］。TANAKA 等提出了一种改进的算子分裂技术，实现了沿着流线方向的速度方向和对流方程的同时求解［6］。BRATVEDT 等将溶剂模型应用到流线数值模拟方法中［7］。

在中国，侯健等最先引入流线方法，建立了聚合物驱和CO2混相驱流线模型［8］。高春光基于坐标变换和镜像反演理论，研究了五点和九点井网模式的渗流问题，分析了等势线和流线的特征［9］，为各向异性油藏井网优化提供了理论依据。何应付等建立了各向异性油藏渗流的数学模型，提出了一种注采井间流线追踪的流线生成方法，得到了各向异性储层的流线分布［10］。张丽等结合渗流力学理论和数值模拟方法，获得了五点井网的流线分布［11-12］。冯其红等研究了各向异性储层的压力场和速度场，使用Pollock 流线追踪法建立了三维两相流体流线模拟方法［13-14］。刘洪等建立了基于形函数插值方法的流线追踪方法，揭示了油藏开发中流线的变化规律［15］。谢伟伟等采用压降叠加原理结合流函数的方法，得到了反九点井网的流线分布［16-18］。叶双江等建立了流场数学模型，通过势函数和流函数，得到了五点法混合注采井网内部等势线和流线分布［19-20］。贾虎等通过流线聚类的方式对不同类型的流场进行了区分评价，采用流线模拟方法对碳酸盐岩油藏水驱流场进行了识别和优化［21］。冯其红等通过提取流线属性数据，构建了表征水驱油能力的流场潜力系数，提出了基于瞬时流场潜力系数的水驱开发效果评价方法［22］。蔡晖等通过特征分级点法对流场进行分级，建立起“三点四级”指标流场表征法［23］。

目前对于流线研究与描述的方法包括电传导实验法、流线油藏工程法、流线数值模拟法等。采用势函数研究流线分布的较少，尤其是依据油藏井网演变模式研究流线分布［24］的更鲜见报道。笔者以x油藏井网调整模式为依据，基于势函数理论，建立了反九点井网加密至排状注采井网的流线模型，研究了考虑储层非均质性和压实作用的井网加密前后的流线演变特征。

1 基于势函数的反九点井网加密前后的流线模型

在前人通过势函数对流场研究［25］的基础上，考虑平面上各处的渗透率差异以及流体黏度变化对流线的影响，通过势函数研究反九点井网加密前后的流场分布。

由达西定律可知，平面渗流场中任一点的渗流速度分量可写为：

由势函数的定义可知：

考虑势函数的渗流速度分量为：

地层中任意一点的渗流速度可以表示为：

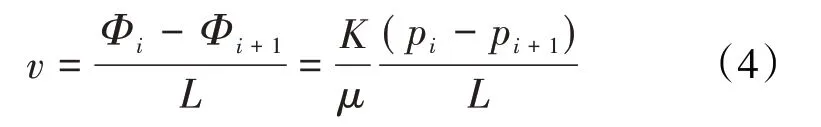
渗流速度的方向是等势线的法线方向，指向压力递减的方向。

势函数与渗流速度存在（3）式的关系，因此势函数也称为速度势。等压线上各点的势函数相等，它是势函数的等值线。势函数满足拉普拉斯方程：

由流函数的定义可得：

由（3）和（6）式可得：

势函数和流函数均满足拉普拉斯方程，在平面渗流场上这2个函数是调和函数。

沿着等势线，势函数的全微分表达式为：

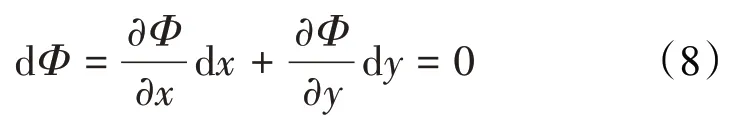
势函数任一点上切线的斜率为：

沿着流线，流函数的全微分表达式为：

流函数任一点上切线的斜率为：

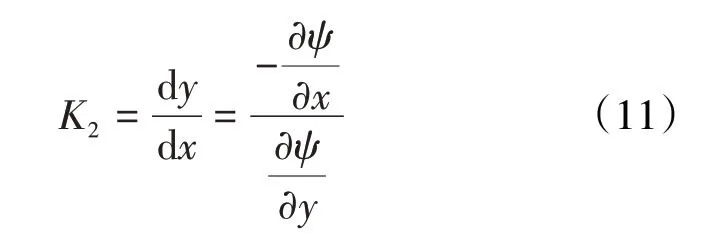
由柯西-黎曼条件可得：

（12）式表明流线与等势线在平面渗流场中任意一点上是互相正交的。根据实验测试可以获得压力场分布［24］，计算得到平面渗流场的等势线分布，进而根据流函数与势函数之间的关系得到流线的分布。

采用流函数确定反九点井网的流场时，对于非均质储层，平面上任意一点的渗透率难以获取，为便于计算，主要考虑了注采井附近的渗透率，同时上述方法没有考虑流体黏度变化的问题。在已知注采井附近渗透率的基础上，平面上任意一点的渗透率采用克里金插值法计算得到，此种方法得到的渗透率可用于非均质模型流线的研究。在水驱油过程中，储层中存在3 个区域，即纯水区、油水共渗区以及纯油区。在开发过程中，油藏各处的油水相渗透率是不断变化的。

流体在3 个区域流动时，渗透率和流体黏度将发生变化，势的计算应该分区考虑：

不同含水饱和度下的渗透率可以结合相对渗透率曲线进行求取，油相相对渗透率与含水饱和度的关系为：

由（14）式可得油相渗透率：

同样水相渗透率可以表示为：

对于流体黏度，目前常用的研究方法是将其设为定值，但随着开发的进行，储层中流体黏度是不断变化的。纯水区的流体黏度以地层水黏度为依据，纯油区的流体黏度以原油黏度为依据。油水共渗区的流体黏度是一个变量，受到地层压力和温度的影响。研究中温度为定值，主要考虑压力变化对流体黏度的影响。而压力变化对地层水黏度的影响较小，因此主要考虑压力对地层原油黏度的影响，其表达式为：

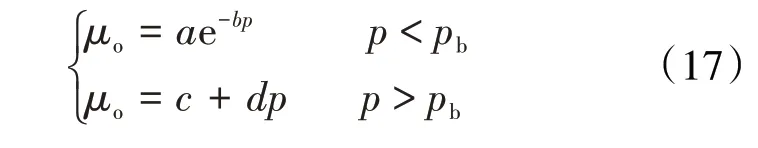
将不同含水饱和度下的渗透率以及对应压力下的流体黏度分别代入（13）和（4）式可以得到非均质模型的势函数和渗流速度，其表达式分别为：

通过（18）和（19）式可以得到流体在地层中各点的势及渗流速度，渗流速度方向为等势线的法线方向，指向压力减小的方向，进而可以获得各方向上的流线分布。

油藏在开发过程中会发生再压实作用［26-27］，在进行流线模拟研究时应考虑再压实作用对流线分布的影响。针对测试模型，压实过后井组各处的渗透率均变小，生产井处的渗透率降幅最为明显，其次为生产井间区域和注采井间区域。根据测试数据，拟合得到地层渗透率与地层压降的关系，进而得到受压实作用影响的势函数和渗流速度的表达式。

将地层压降与开发过程中的最大压降的比值定义为压实系数，油、水相渗透率与压实系数存在较好的线性关系，二者的关系式为：

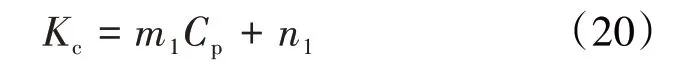
将（20）式分别代入（18）和（19）式，得到考虑压实作用的势函数和渗流速度的表达式分别为：

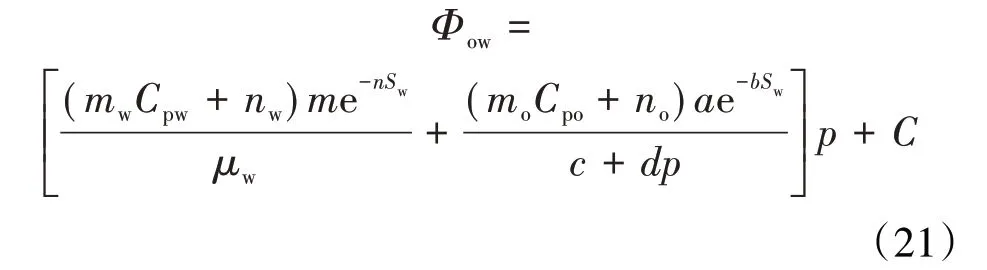
2 反九点井网至排状注采井网流线演变特征

由采用势函数流线模型计算的均质模型井网加密前后的等势线和流线的分布（图1）可以看出，基础井网和加密井网的势在注入井周围（图1 中红色部分）最高，采出井（图1 中蓝色部分）最低，势从注入井向采出井逐渐降低；注采井之间的流线比较规则，对称分布。主流线区域和流线分割区与谢伟伟采用流函数模型计算的均质模型［16］的流场较为一致。对于反九点井网主流线主要分布在注采井间渗流通道上，而边角井之间区域流线相对稀疏，且角井流线控制范围相对边井稍小。对于排状注采井网，模型流场发生显著变化，中间井排转注使得注采井之间的流线均匀分布。

图1 均质模型井网加密前后等势线和流线分布Fig.1 Equipotential line and streamline distribution before and after well pattern infilling in homogeneous model

由非均质模型井网加密前后等势线和流线分布（图2）可见，模型的流线分布发生不规则变化，形态与均质模型流线存在较大差异，主要是计算时考虑了平面渗透率的差异以及流体黏度变化的影响。各注采井间流场分布差异较大，受井间物性差异影响，主流线并不完全沿生产井方向分布，注入水优先沿高渗透带突进。由于低渗透区的存在，流体会发生绕流，与均质模型相比，主流线方向多变，流场分布更为复杂。从流线的角度可以看出，反九点井网边角井之间的流线分割区水驱效果较差。

图2 非均质模型井网加密前后等势线和流线分布Fig.2 Equipotential line and streamline distribution before and after well pattern infilling in heterogeneous model

加密后，非均质模型与均质模型的流线分布整体表现出相似的流动规律，从注水井排向生产井排波及。但2 口转注井与采出井的流线存在差异，右侧转注井位于低渗透区，流量较小，流线相对稀疏，而左侧转注井靠近高渗透带，注入水流量较大，流线分布相对密集。由于受到储层非均质性的影响，流向边角井的流线呈现不规则的形态，转注加密后流向边角井的流线分流，流向加密井的流线增加。同样，从流线演变特征可以看出，反九点井网的流线分割区位于加密井网的主要流动区，加密后，注入水与加密井之间的流线穿越了该部分区域，井网水驱控制程度得到改善，原先驱替效果差的区域受到注入水的波及。排状注采井网的不可动区域位于反九点井网的主流线区域，在反九点井网的开发过程中已经受到注入水的驱替。排状注采井网原采油井排采油井与加密井之间的流线分割区以及加密前后流线分割区的叠合区水驱效果较差。

流线是流体流动规律的综合反映，流体在流动中受到驱替压力、渗透率、流体黏度等因素的影响，而储层非均质性是造成这些因素差异的主要原因。因此，这种处理方式得到的流线分布对储层非均质性的反映程度较高。

疏松砂岩油藏在开发过程中，随着地层流体的采出，地层压力下降会导致地层压降增大从而引起储层压实，储层岩石和流体的受力平衡遭到破坏进而引起储层物性的改变，物性的变化会影响油水的渗流特征，反映到流场上的表现是压实前后流线分布的变化。储层的压实作用［26］主要发生地层压力下降显著的生产初期，而后随着注入水的增加，地层压力升高，储层物性得到保持。因此，主要研究了反九点井网压实作用前后的流线分布特征。

通过（21）和（22）式计算得到受储层压实作用影响的势函数和渗流速度，进而得到压实作用下的流线分布。由于井组各处压实程度不同，压实后流线发生不规则变化。由非均质模型反九点井网压实前后的等势线和流线分布（图3）可见，角井区域的压实作用相对明显，在流线上的表现是压实后流向角井的流线减少，角井的水驱控制面积减小。压实作用会引起流线流动方向的改变，原来的渗流通道被压缩甚至闭合，流体流动的连续性遭到破坏，从而发生绕流。注水井周围能量补充较为及时，压实作用较弱，压实作用对注水井周围的流线影响较小。流线分布显示压实对角井、边井的影响较为显著，对注水井的影响最弱，但对采油井之间滞留区、注采井区间流线的影响并不明显。

图3 非均质模型反九点井网压实前后等势线和流线分布Fig.3 Equipotential line and streamline distribution of inverted nine-spot pattern before and after compaction in heterogeneous model

3 模型可靠性验证

为了验证模型的可靠性，采用商业软件Eclipse中的FrontSim 模型，进行基于实验模型的反九点基础井网及加密井网的流线数值模拟。与图2 相比，整体上看，反九点井网和排状注采井网的数值模拟流线分布（图4）显示，势函数非均质模型得到的注采井之间的流线分布规律与数值模拟软件的模拟结果显示的规律相似，不同注采井之间的流线边界、流线控制区域形状、控制区域大小相似，表明基于势函数建立的反九点井网加密前后的流线模型是可靠的。

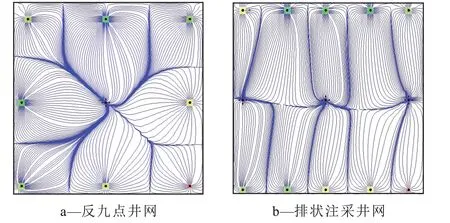
图4 非均质模型井网加密前后数值模拟流线分布Fig.4 Streamline distribution before and after well pattern infilling in heterogeneous model by numerical simulations

4 结论

基于势函数理论，推导了反九点井网排状加密后的井网流线模型，得到了反九点井网转排状注采井网的流线演变特征。

考虑储层非均质性和压实作用，基于势函数流线模型对反九点井网加密前后的流场变化进行研究。该模型得到非均质模型的流线与实际流场较为符合，可以较好地反映储层的非均质性。压实后由于井组各处压实程度的差异，流线发生不规则变化。流线分布显示压实对角井、边井的影响较为明显，对注水井的影响最弱，但对采油井之间滞留区、注采井区间流线的影响并不明显。

考虑平面渗透率和流体黏度的变化，通过势函数获得的流线分布可以较好地还原储层非均质条件下的流场。流线演变特征显示反九点井网边角井之间的流线分割区、排状注采井网原采油井排采油井与加密井之间的流线分割区以及加密前后流线分割区的叠合区水驱效果较差。

符号解释

a，ai，ai+1，b，bi，bi+1，d——系数；

c，C，C1，C2，C3——常数；

Cp，Cpi，Cpi+1，Cpo，Cpw——压实系数；

i——自然数；

K——渗透率，mD；

Kc——绝对渗透率，mD；

Kci，Kci+1——非均质模型平面上不同位置处的绝对渗透率，mD；

Ko——油相渗透率，mD；

Kro——油相相对渗透率；

Kw——水相渗透率，mD；

K1——势函数任一点上切线的斜率；

K2——流函数任一点上切线的斜率；

L——2条等势线间的距离，cm；

m，m1，mi，mi+1，n，n1，ni，ni+1——拟合系数；

mo，no，mw，nw——油、水相有效渗透率与压实系数的拟合系数；

p——压力，MPa；

pb——饱和压力，MPa；

pi，pi+1——等势线对应压力线的压力，MPa；

Sw——含水饱和度；

Swi，Swi+1——非均质模型平面上不同位置处的含水饱和度；

v——地层中任意一点的渗流速度，cm/s；

vx，vy——x，y方向的渗流速度，cm/s；

x，y——坐标轴方向；

μ——流体黏度，mPa·s；

μo——油相黏度，mPa·s；

μw——水相黏度，mPa·s；

Φ——某一点的势，J；

Φi，Φi+1——2条等势线的势，J；

Φo——纯油区的势，J；

Φow——油水共渗区的势，J；

Φw——纯水区的势，J；

ψ——流函数。