Numerical Study for Magnetohydrodynamic(MHD)Unsteady Maxwell Nanofluid Flow Impinging on Heated Stretching Sheet

Muhammad Shoaib Arif,Muhammad Jhangir,Yasir Nawaz,Imran Abbas,Kamaleldin Abodayeh and Asad Ejaz

1Department of Mathematics and Sciences,College of Humanities and Sciences,Prince Sultan University,Riyadh,11586,Saudi Arabia

2Department of Mathematics,Air University,Islamabad,44000,Pakistan

ABSTRACT The numerous applications of Maxwell Nanofluid Stagnation Point Flow,such as those in production industries,the processing of polymers,compression,power generation,lubrication systems,food manufacturing and air conditioning,among other applications,require further research into the effects of various parameters on flow phenomena.In this paper,a study has been carried out for the heat and mass transfer of Maxwell nanofluid flow over the heated stretching sheet.A mathematical model with constitutive expressions is constructed in partial differential equations(PDEs)through obligatory basic conservation laws.A series of transformations are then used to take the system into an ordinary differential equation (ODE).The boundary conditions (BCs) are also treated similarly for transforming into first-order ordinary differential equations(ODEs).Then these ODEs are computed by using the Shooting Method.The effect of factors on the skin friction coefficient,the local Nusselt number,and the local Sherwood number are explored,and the results are displayed graphically.The obtained results demonstrate that by increasing the values of the Maxwell and slip velocity parameters,velocity deescalates.For investigators tasked with addressing unresolved difficulties in the realm of enclosures used in industry and engineering,we thought this work would serve as a guide.

KEYWORDS Maxwell fluid;stagnation point flow;heat and mass transfer;thermal radiations;shooting method

Nomenclature

u(m/s)Horizontal Velocity

αThermal Diffusivity

v(m/s)Vertical Velocity

τThe Ratio of Heat Capacity of Base Fluid to the Nanoparticles Heat Capacity Coefficient

λ1(s)Relaxation Time of Maxwell’s Fluid

σ∗Stefan-Boltzmann Constant

k∗Mean Absorption Coefficient

B0(kg/(m2.s2))Strength of Magnetic Field

δUnsteady Parameter

βMaxwell Parameter

∊Stretching Parameter

PrPrandtl Number

RThermal Radiation Parameter

NbBrownian Motion Parameter

NtThermophoresis Parameter

ScSchmidt Number

MMagnetic Parameter

fwSuction/Injection Parameter

Cw(x,t)Volume Fraction of Nanoparticles at the Sheet

C∞Volume Fraction of Nanoparticles Farther Apart from the Sheet

Tw(x,t) (K)Temperature at the Sheet

T∞(K)Temperature Farther Apart from the Sheet

1 Introduction

It is a fact that our earth is covered with a hundred per cent air and approximately seventy per cent water.Since water and air are fluids,fluids have great significance in our lives.Archimedes was the mathematician who examined the statics and buoyancy of the fluids.Researchers have shown their great interest in non-Newtonian fluids during the last few decades.Non-Newtonian fluids are the most critical fluids because of their enormous applications in biological sciences,food processing industry,geophysics,oil pipelines,chemical industry,rocket engines,air conditioning systems,petroleum industry,wind turbines,etc.The flow behaviour of non-Newtonian fluids is modified under stress.Most numerous fluids used in biomedicine and industry are non-Newtonian.Some familiar examples are blood,ink,honey,shampoos,slurries,printer,and cosmetic products.Using the Navier-Stokes equations and their constitutive relationship,we may better understand the rheological individuality of Newtonian fluids;on the other hand,non-Newtonian fluids have very different flow characteristics than Newtonian fluids.Several researchers have applied 2D translational magnetohydrodynamic(MHD)techniques to the movement of Maxwell’s convection and discovered that these phenomena were important factors in 2D fluid flow caused by gravitational waves.To explore the thermal and mass transfer properties in 2D transient Maxwell nanofluid flow induced by stretching cylinder magnetic field are considered in[1].

Nanofluids are used extensively in nanoscience,including building materials,military equipment,nano machining of nanowires and nanorods,etc.In this regard,the following studies can be consulted[2,3].Hayat et al.tried to figure out the flow of second-grade fluid,non-linear surface stress,convective heat,and keeping property of various skins with a tool designed to analyze flow convection[4].The properties of flow in non-linear geometries were investigated with nanofluid properties for small region solutions [5,6].Ahmed et al.[7] studied the MHD Magneto hydrodynamic fluid flow through a porous medium with this high surface-to-volume colloidal hydromagnetic nanofluid analysis.The effects of non-linear thermal radiation,convective conditions,and heat generation/absorption at the boundary are investigated to determine whether synergies exist.MHD is a term that refers to the study of electrically conducting fluid dynamics.This is accomplished by combining the Navier-Stokes equations for fluid dynamics and Maxwell’s equations for electromagnetism.One of the MHD’s important innovations was the recognition that magnetic fields can create currents in a fluid conductor,which induce corresponding currents in the fluid,producing magnetic forces on the fluid.In the presence of zero normal streams of nanoparticle speed-slip boundary conditions,the numerical analysis of stagnation-point flow,convectional heat transmission to the tan-gent nanofluid was studied by Vittal et al.[8].Numerical surveys on unsteady magnetohydrodynamic MHD in permeability over a stretched sheet with reaction boundary and suction/injection boundary have been studied by Shravani et al.[9].Srinivas et al.[10] investigated the effects of Soret and convective boundary conditions on MHD pulsating flow in a horizontal channel using an analytical solution based on the perturbation technique.Ramesh et al.[11]analyzed to determine the Maxwell fluid stagnation point in the presence of nanoparticles and a permeable stretching sheet.

Magnetohydrodynamic fluid flow and heat transfer problems for a vicious and incompressible dusty fluid conductor over an unstable stretch panel are solved using numerical analysis by Manjunatha et al.[12].The effect of heat generation and absorption on tangent hyperbolic nanofluid at the stagnation point over a stretching cylinder was studied by Salahuddin et al.[13].The unpredictability of MHD free convection flow was investigated by Ahmmed et al.[14].In the presence of radiation,a nanofluid flows through an exponentially accelerated inclined plate embedded in a porous material with variable thermal conductivity.The work presented in [15] investigates the Newtonian heating properties of a viscous nanomaterial in a permeable stretched flow.In[16],Mondal et al.presented a model for the Maxwell nanofluid’s unstable flow through a permeable,convective border shrinking plate and heat transfer.

Nanofluids are suspensions of solid particles whose diameters range from 1 to 100 nm.Nanofluids,including base fluids and nanoparticles,are taken as a subclass for heat transfer fluids.In nanofluids,the nanoparticles are generally made up of nano metals,for instance(carbon,graphite)or metals like Al2O3,(Al,Cu) oxides,nitrides (AlN,SiN).Nanofluids are adequately viscous,steady enough against wetting,dispersing,and bear spreading characteristics on solid surfaces,even for modest nanoparticle fixation.These are used to increase the thermo-physical characteristic like heat transfer,viscosity,thermal diffusivity,and base fluid conductivity such as ethylene glycol,propylene glycol,water,etc.With a low concentration (1–5) percent,the thermal conductivity of solid nanoparticles is increased by about 40 percent.It has several applications in engineering and biotechnology,like cancer therapy and the cooling process in industries.These become the two-phase system due to solid and liquid.Many articles have been published to study nanofluids’increased heat transfer capabilities[17–23].Mustafa et al.[24]discussed thermophoretic Brownian motion and the magnetic field’s consequences on the mixed convective flow of magneto-nanofluid that is hurdled by an extendable vertical surface.Hayat looked at the impact of chemical reactions in magnetohydrodynamic flow through a non-linear radially stretching surface.The author concluded that the Nusselt number depends on the power-law index and increases the power-law index function.

Atif et al.[25] presented the idea of magnetohydrodynamic micro polar Carreau nanofluid and reported that thermal profile escalates for larger values of the Brownian motion parameter.Dogonchi et al.[26]considered thermal flux and thermal radiation consequences and MHD nanofluid heating over a stretching sheet Joule Heating.Cattaneo Christov’s heat flux model investigates heat transfer characteristics.Finally,Reddy et al.[27]explored a similar solution in the existence of Thermophoresis and Brownian parameters for hydromagnetic movement of a nanofluid over a slandering stretching sheet.Dogonchi et al.[28]recently investigated the effect of radiation on the heat transfer of nanofluid flow using permeable media.He observed an increment in the velocity and reduction in the temperature profile by enhancing the Reynolds number and expansion ratio.It was stated that the heat transfer rate increases directly by escalating the values of mixed convection parameters.The effects of thermal radiation on nanofluid flow have also been discussed by Sheikholeslami et al.[29,30].The characteristics of heat transfer and fluid flow,taking into account the nanofluids,were studied in detail by several researchers[31–34].Recent papers have given several investigations in convective transport using nanofluids in external flow and boundary layer flow[35–38].

Many researchers put their valuable investigations on the Maxwell nanofluids’flow and their further types using different sheets [39–43].Bilal et al.[44] examined the continual heat and mass transfer features generated by an inclined-cylinder diffusion,heat fluids,convective heating effects,and joule heating effects.Lu et al.[45]studied entropic generation with the effect of magnetic dissipation and transpiration in the dissipative flow of nanofluids.The primary objective of[46]is to investigate the Brownian motion and heat-forging effects on micropolar nanofluid flow on a non-linear inclined stretch sheet while accounting for the effects of Soret and Dufour.In the presence of a non-uniform heat source/sink,the Carreau nanoparticle thin film’s thermodynamics is being studied by Khan et al.[47].In this study,in the presence of suction,heat radiation,and a heat source/sink,Jamaludin et al.[48]numerically investigated the stagnant convection mixture-point flow nanofluid over a vertical stretching/shrinking sheet.Bagherzadeh et al.[49] investigated the effect of a magnetic field on the hot injection of dispersed nanoparticles into a microchannel via a micro cross.According to Jalali et al.[50],oil nanofluid jet injection into a rectangular microchannel was studied for heat transfer.Hajatzadeh Pordanjani et al.[51]examined the effect of free convection in the cavity of the thermal field and thermal radiation of the thermal transfer and entropy generation of nanofluid.

The flow of an incompressible viscous fluid across a flat deformable sheet with a velocity proportional to the distance from the stagnation point is studied in[52].The work in[53]investigated the steady two-dimensional stagnation point flow of an incompressible micropolar fluid over a stretching sheet when the sheet is extended in its own plane.The flow of an incompressible micropolar fluid over a non-linear stretching surface is investigated in two dimensions [54].For boundary layer flow over nonlinearly extending sheets,an analytical solution has been provided by the shooting approach in[55].Variable transverse magnetic field,viscous dissipation,thermal radiation,and a nonlinearly flowing free stream were all considered in the flow analysis.The effect of viscous dissipation has also been considered in[56]for Williamson nanofluid under the effects of multiple slips and Joule heating.The resulting system of ordinary differential equations has been tackled with the shooting method based on the Runge-Kutta-Fehlberg method.Local skin friction coefficients,local heat transfer rates,and mass transfer rates are shown in the tables below.According to[57],a shooting strategy based on the 4thorder Runge-Kutta Gill method was used to solve a set of non-linear ordinary differential equations generated by viscous dissipation.Hybrid nanoparticles’influence on velocity and temperature profiles has been given in[58]over a stretching sheet.The non-linear thermal radiation in the energy equation has been considered despite linearized thermal radiations.The differential transform method has been employed to solve the set of ordinary differential equations that arise in the MHD Williamson fluid with chemical reaction[59].It was observed that Williamson’s fluid parameter and magnetic strength produce a thicker boundary layer for velocity.Another analytical research based on the homotopy analysis method was presented for the two-dimensional steady,incompressible flow of the Oldroyd-8 constant [60].The homotopy analysis method is based on homotopy that contains a parameter for controlling the convergence of solution series.The method finds the solution of linear and non-linear ordinary and partial differential equations in components form.The study of entropy optimization of MHD coupe stress nanofluid slip flow and heat&mass transfer on entropy generation has been given in[61,62].Recent research on boundary layer fluid flow problems is available in[63–66].

The study comprises an extension of the previously constructed model for MHD boundary layer flow.The effects of Maxwell fluid and velocity slip are considered with the existing model.The previous study has consisted of an analytical approach,but in this study,a numerical method based on the Runge-Kutta method and Newton Raphson method.The combination of these methods is called the shooting method,which can find missing initial conditions.

The strategy of this paper is as follows:

We examine classical definitions and a history of unstable boundary layer flow 2-D MHD in Section 2.In Section 3,numerical results are presented using different numerical techniques.Results and discussion are presented in Section 4.Section 5 sums up the findings.

2 Governing Equations

The presented model aimed to investigate a 2-D MHD unsteady boundary layer flow considering the Maxwell nanofluid by considering the fluid flow over a porous stretching surface.Moreover,the impacts of thermal emission and magnetic fields are considered.The 2-D Cartesian coordinate system is taken so thatx-axis is taken along the flow andy-axis is taken normal to the sheet.To stretch the sheet in a fixed region,along thex-axis two spontaneous forces are applied,opposite in direction but equal in magnitude.At timet=0,the fluid flow is steady.However,for a timet>0,it will become unsteady.An incompressible and laminar flow is bounded in the section specified asy >0.The sheet is stretched towards thex-axis with velocityUw(x,t)=here the stretching rate is denoted byawhereλis a positive constant with axiomλt<1.Ue(x,t)=is the velocity of the ambient fluid.There will be no slip between nanoparticles and base fluid for thermal equilibrium.But for electrically conducting fluid∗(Lorentz force) is acting on the fluid here,the transverse magnetic field is denoted by=(0,B,0).The simplified Lorentz force is −σB20(u−Ue),B=is the magnetic field perpendicular to the sheet.According to[63],the induced magnetic field is discarded due to the small magnetic Reynolds number.Also,neglect the induced electrical field due to the polarization of charge,and there does not exist external electric field.The geometry of the problem is given in Fig.1.The constitutive PDEs for continuity,momentum,energy,and concentration are given below:

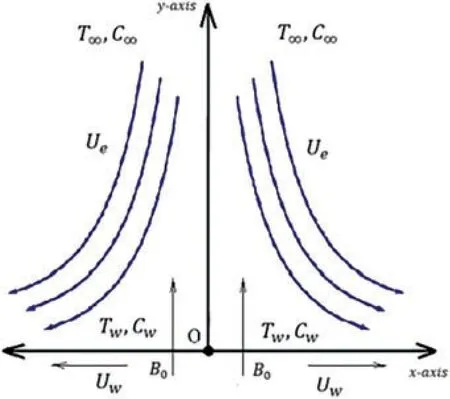
Figure 1:Geometry of the problem

In Eq.(3),a linearized Rosseland radiative flux is considered whose linearized form is given by:

whereτ=At the boundary,the conditions for the model,as mentioned earlier,are as follows:

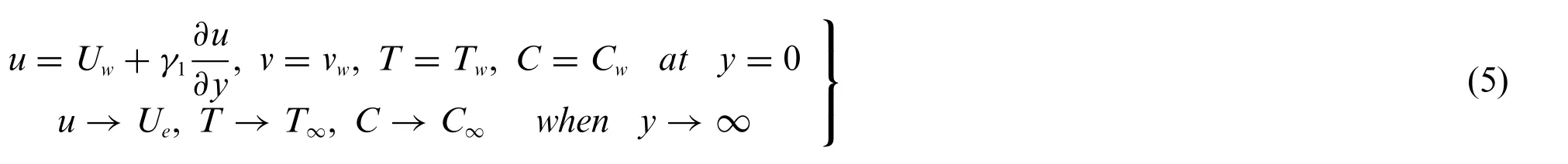
whereγ1is the slip coefficient while the velocity of suction/injection is denoted byvw=At the boundary,assume the sheet’s temperature and nanoparticles volume fraction as[34]:

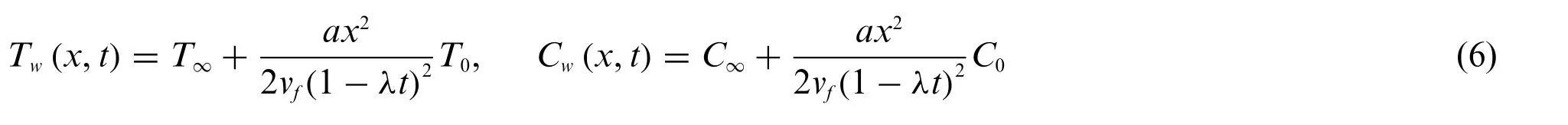
HereT0is a positive reference temperature,andC0is positive reference nanoparticles volume fraction such thatTw >T0>0 andCw >C0>0,these expressions are valid only if 0<(1 −λt).Now,non-dimensional variables are defined as[34]:

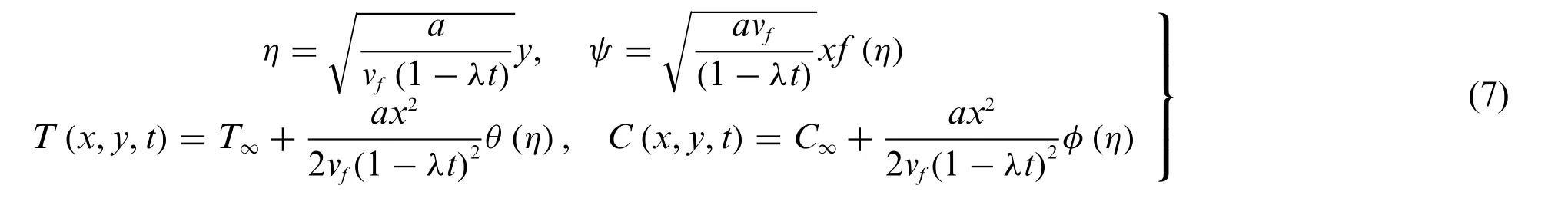
The components of velocity are defined as[34]:

Here differentiation with respect toηis denoted by prime.Now using Eqs.(6) and (7) into dimensional Eqs.(2)to(4),the following non-dimensional system of ODEs can be obtained:

Eqs.(3)–(4) &(9)–(10) are same given in [34].The transformed non-dimensional boundary conditions are:

where parameters are given below:

Dimensional skin friction coefficient (without the effect of Maxwell fluid),local Nusselt and Sherwood numbers are as under:

The non-dimensional forms of Eqs.(12)to(14)can be expressed as:

Here the Reynolds number is:

3 Numerical Treatment

The present section is related to the implementation of the shooting method.A system of higherorder ODEs is converted into first-order ODEs along with the boundary conditions.The shooting method is based on applying the Runge-Kutta method to discretize the set of ordinary differential equations.The Newton Raphson method is employed to find missing initial conditions.Since the Runge-Kutta method is applied to first-order differential equations,the equations are reduced into first-order differential equations.

Following notations are used for converting Eqs.(8)–(10)into first-order ODEs:

f=g1,f′=g2,f′′=g3,θ=g4,θ′=g5,φ=g6,φ′=g7

Now using the above notations,we convert Eqs.(8)–(10)into a system of first-order ODEs along with their given and assumed boundary conditions:

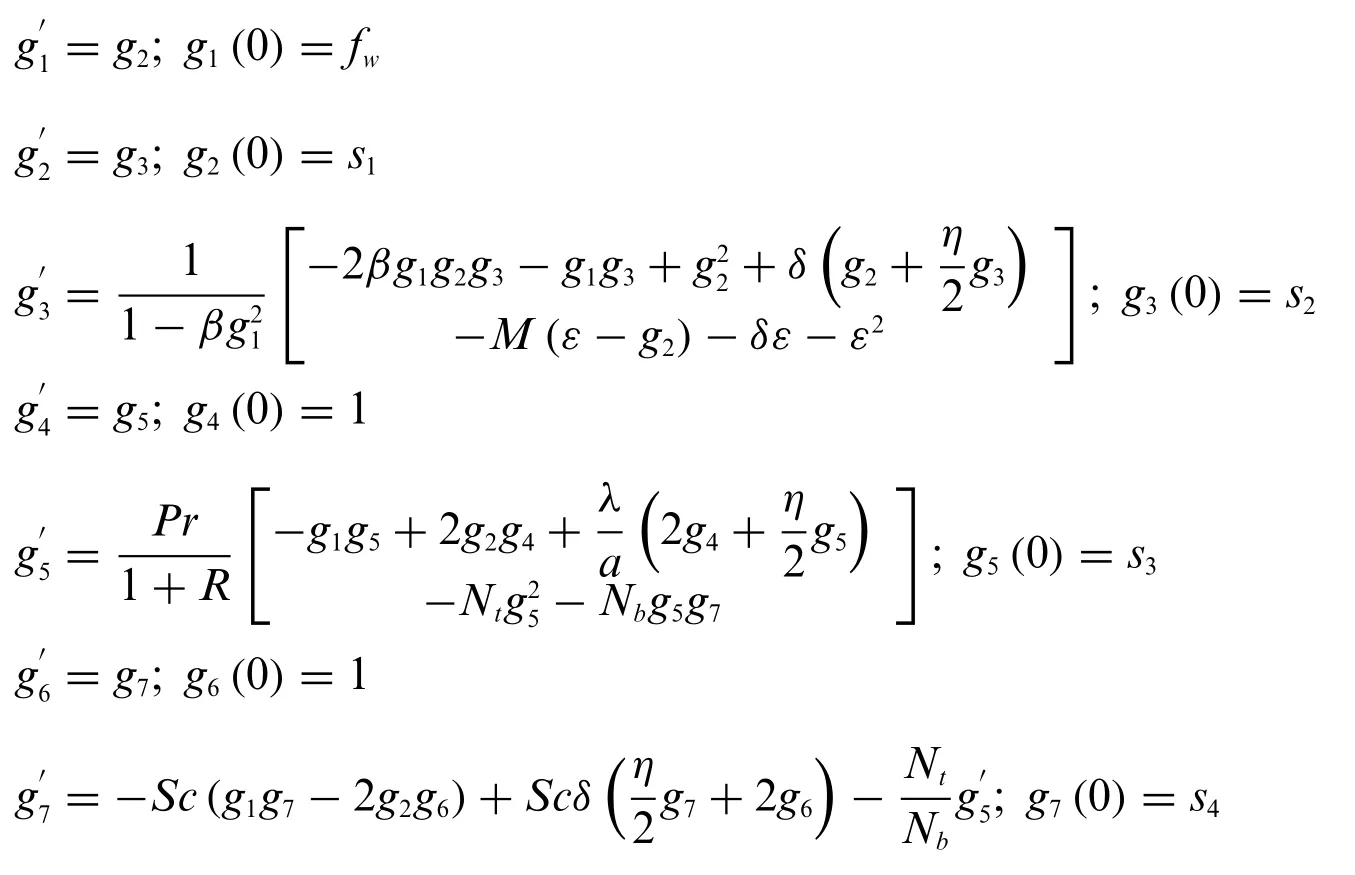
The approximate solution of the above first-order ODEs is obtained by incorporating the RK-4 method and an iterative method.The chosen domain for the problem is[0,η∞].Hereη∞is a finite real number such that variation for solution inη >η∞is ignorable.Newton’s iterative scheme is used to solve the algebraic equations,which is given as follows:

wherei=1,2,3&j=3,5,7.If we meet the criterion:

Then we will stop the computational processes;otherwise,we continue using the Newton iterative scheme to refine the initial guess.Hereε0is a very small positive number.

4 Result and Discussion

We thoroughly discuss approximated results of Skin-friction,Nusselt number,and Sherwood number through graphs.Calculations were carried out to influence different non-dimensional parameters likeM,Nb,Nt,ScandRthrough the shooting method.Moreover,the impact of these parameters on concentration,temperature,and velocity profiles is also considered via graphs.

Fig.2 is defined for various values ofMagainst the non-dimensional velocity profile.We observed that the non-dimensional velocity profile escalates with the escalation of magnetic parameterM.Also,the velocity profile was found to be a decline for suction.Fig.3 is plotted in the existence of injection.To delineate the impact of parameterMon non-dimensional velocity,the velocity profile seems to decline for the rising values ofM.It appears to decline for the escalating values ofM.

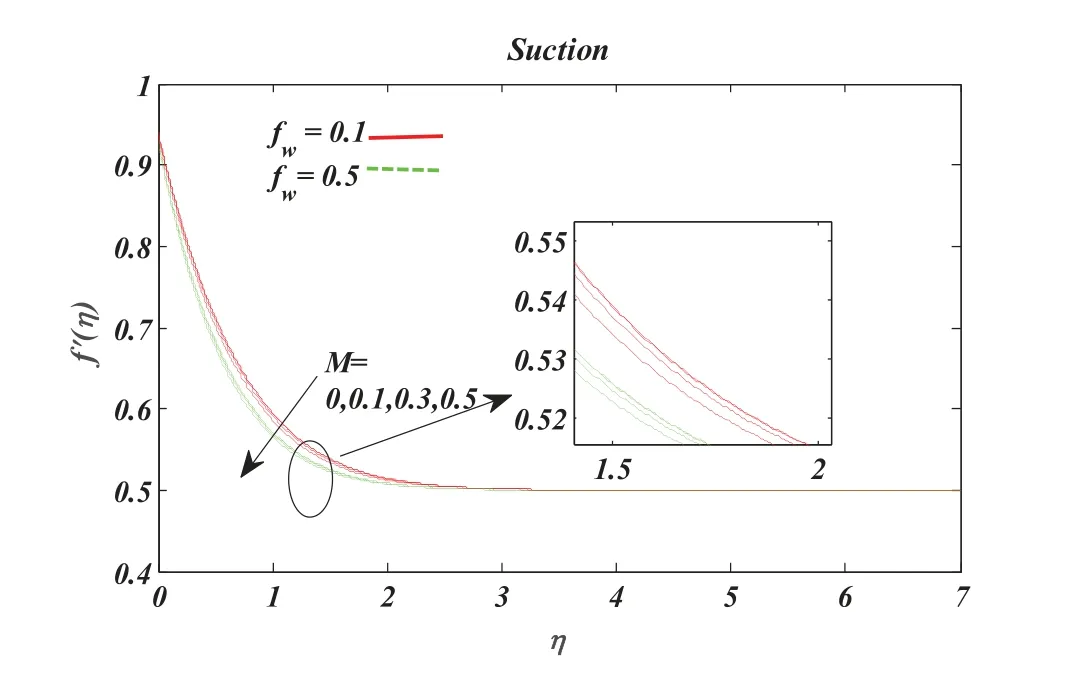
Figure 2:Effect of magnetic parameter M on f ′(η)

Figure 3:Effect of magnetic parameter M on the velocity profile using Pr=1.2,ε=0.1,Nb=Nt=0.2,Sc=01,R=0.5,δ=0.1,β=0.2

The effect ofδfor various values on non-dimensional velocity profiles is displayed in Figs.4 to 5.With the rise in unsteady parameterδ,the non-dimensional velocity deescalates and escalates,respectively,for suction and injection.Figs.6 and 7 are plotted for the dimensionless velocity against the different values of Maxwell parameterβfor suction/injection.The figures reflect that the dimensionless velocity profile deescalates and escalates for suction and injection with the Maxwell parameterβ.

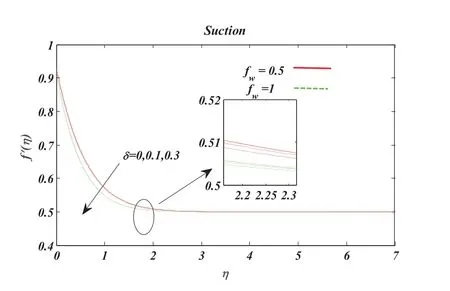
Figure 4:Effect of unsteady parameter δ on the velocity profile using Pr=1.2,ε=0.1,Nb= Nt=0.2,Sc=01,R=M=0.5

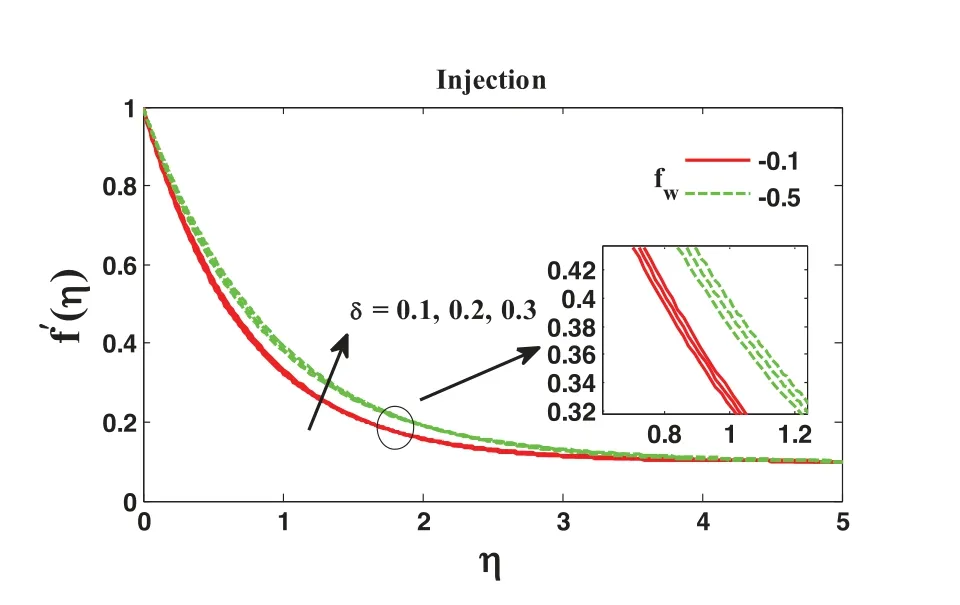
Figure 5:Effect of unsteady parameter δ on the velocity profile using Pr=1.2,∊=0.1,Nb= Nt=0.2,Sc=01,R=M=0.5

Figure 6:Effect of maxwell parameter β on the velocity profile using Pr=1.2,∊=0.1,Nb= Nt=0.2,Sc=01,R=M=0.5,δ=0.1

Figure 7:Effect of maxwell parameter β on the velocity profile using Pr=1.2,∊=0.1,Nb= Nt=0.2,Sc=01,R=M=0.5,δ=0.1

Figs.8 and 9 are framed to delineate the effect of parametersfWandMon non-dimensional temperature distributionθ(η).Fig.8 exhibits that the temperature distribution escalates with the escalation in various values in the magnetic parameter and the suction parameterfW.Similar behaviour has been observed for injection in Fig.9.The dimensionless temperature profile is enhanced due to the transverse magnetic fieldMbecause the flow field is reduced due to magnetic parameterMin both cases.

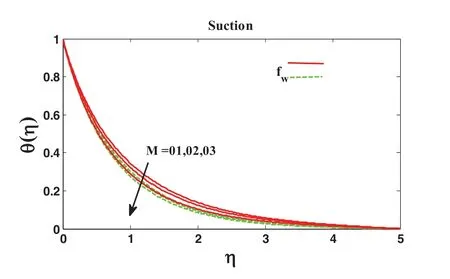
Figure 8:Effect of magnetic parameter M on the velocity profile using Pr=1.2,∊=0.1,Nb=Nt=0.2,Sc=01,R=0.5,δ=0.1,β=0.2

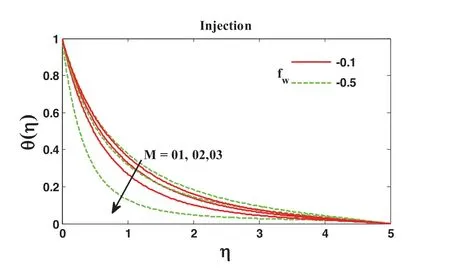
Figure 9:Effect of magnetic parameter M on the temperature profile using Pr=1.2,∊=0.1,Nb=Nt=0.2,Sc=01,R=0.5,δ=0.1,β=0.2

Fig.10 demonstrates the impact of the parametersRandδon the non-dimensional temperature profile.It is clear from Fig.10 that a large estimation of the parameterδdeescalates the nondimensional temperature for the inner thermal boundary layer.Resultantly,the thermal boundary layer thickness is decreased.Moreover,an increment inRescalates the heat flux from the sheet,which upraises the temperature,and consequently,the non-dimensional temperature profile is enhanced with the increment inR.Whereas Fig.10 describes the impact of parametersNtandNbon the nondimensional temperature.As a consequence of the particles’random motion,the particles’collision rate increases.Resultantly,the kinetic energy of the particles enhances.This is transformed into heat energy.Hence with an enhancement in the Brownian motion parameterNb,the non-dimensional temperature escalates.

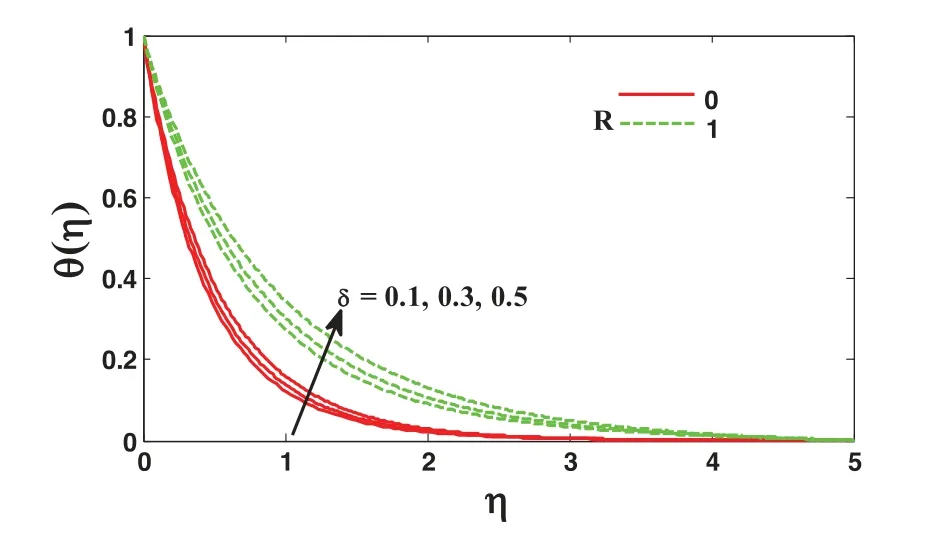
Figure 10:Effect of unsteady parameter δ on the temperature profile using Pr=1.2,∊=0.1,Nb=Nt=0.2,Sc=01,M=0.5,fw=0.5,β=0.2

Similarly,the temperature profileθ(η)seems to incline withNtInclination because the gradient of temperature generates a force.This is because heated fluid shifted away from the surface,which increases the thermophoresis parameterNt.Consequently,the boundary layer temperature seems to be enhanced,as delineated in Fig.11.

Figure 11:Effect of thermophoresis parameter Nt on temperature profile using Pr=1.2,∊=0.1,δ=R=0.1,Sc=01,M=0.5,fw=0.2,β=0.2

Fig.12 delineates the concentration profile with the variation of thermophoretic parameterNtand Brownian motion parameterNb.The concentration profile grows by enhancing thermophoretic and Brownian motion parametersNt&Nb.Similarly,Fig.13 reveals the impact of the thermophoretic parameter and Brownian motion parameterNtandNbon concentration profile.It seems to be a concentration profile upraises by enhancing the values of both parameters.Because increasing the Brownian motion parameter leads to the displacement of nanoparticles from the plate to its surroundings,the concentration profile is elevated.Fig.14 clarifies the impact of velocity slip parameterγon the velocity profile.It seems to be velocity deescalates by decaying the values of the slip velocity parameterγ.Since upraising,the values of the slip parameter upraises the coefficient of shear stress at the plate,which results from resistance in the fluid motion near the plate.So,the velocity of the adjacent layers of the fluid decays.Fig.15 reveals the impact of the Schmidt numberScon concentration profile.The concentration profile deescalates by enhancing Schmidt’s numberScbecause growth in the values of the Schmidt numberSceither grows the kinematic viscosity of different base fluids or decays the mass diffusivity.For the first case of growing viscosity,the fluid’s velocity deescalates,responsible for deescalating the concentration profile for the second case of decaying mass diffusivity.Smaller values of mass diffusivity deescalate the concentration profile due to Fick’s law.Fig.16 exposes the impact of magnetic parameterMand unsteady parameterδon local Nusselt numbers.The local Nusselt number decays by raising the values of magnetic parameterMbecause the rising strength of the magnetic field resists the flow’s velocity.This results in decay in convective heat transfer,so the local Nusselt number decreases.Also,the local Nusselt number grows by enhancing the values of the unsteady parameter.Fig.17 delineates the impact of the Schmidt numberScand Brownian motion parameterNbon local Sherwood number.The local Sherwood number upraises by enhancing the Schmidt number and Brownian motion parameter values.The growth in Schmidt number leads to decay in mass diffusion rate,so the local Sherwood number is enhanced.Also,an increase in the Brownian motion parameter leads to growth in random movements of particles,and therefore convective mass transfer escalates,and thus local Sherwood number increases.Fig.18 demonstrates the impact of thermal radiation parameterRand thermophoretic parameterNton local Nusselt number.The local Nusselt number rises by enhancing the values of the radiation parameter.The reason behind the growth of local Nusselt number is the escalation of conductive heat transfer due to incoming radiations when radiation parameter increases.The local Nusselt number decays by increasing the values of the thermophoretic parameterNt.The growth in the thermophoretic parameter leads to higher thermophoretic force.Consequently,convective heat transfer decreases due to the increment of moving particles from the vicinity of the plate to its surroundings.Fig.19 delineates the impact of magnetic parameterMand suction/injection parameters on the Skin friction coefficient.In Fig.18,the Skin friction coefficient escalates by raising the values of the magnetic parameter for both suction and injection cases.This escalation in skin friction coefficient is the consequence of growth in Lorentz force due to an increase of magnetic parameter,which resists the velocity of the flow.So the wall friction increases,and therefore shear stress at the wall grows.

Figure 12:Effect of brownian motion parameter Nb on concentration profile using Pr=1.2,∊= δ=0.1,R=0.1,Sc=01,M=fw=0.5,β=−0.5

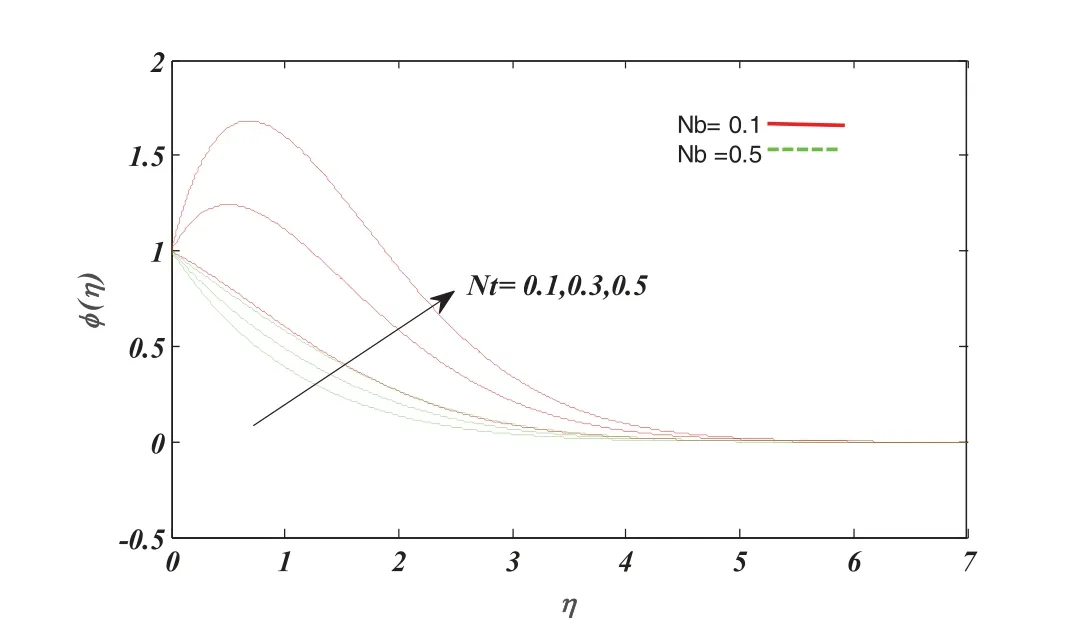
Figure 13:Effect of thermophoresis parameter Nt on concentration profile using Pr=1.2,∊=0.1,Sc=01,R=0.5,δ=0.1,β=0.2

Figure 14:Effect of velocity slip parameter γ on the velocity profile using Pr=1.2,∊=0.1,Nb=Nt=0.2,Sc=01,R=M=0.5,δ=0.1

Figure 15:Effect of Schmidt number Sc on the concentration profile using Pr=1.2,∊=0.1,Nb=Nt=0.2,Sc=01,R=M=0.5,δ=0.1

Figure 16:Effect of unsteady parameter δ &magnetic parameter M on local Nusselt number using Pr=1.2,∊=0.1,Nb=Nt=0.2,R=Sc=1,β=−0.5

Figure 17:Effect of Schmidt number Sc&brownian motion parameter Nb on local Sherwood number using Pr=1.2,∊=δ=0.1,M=fw=R=0.5,β=−0.7

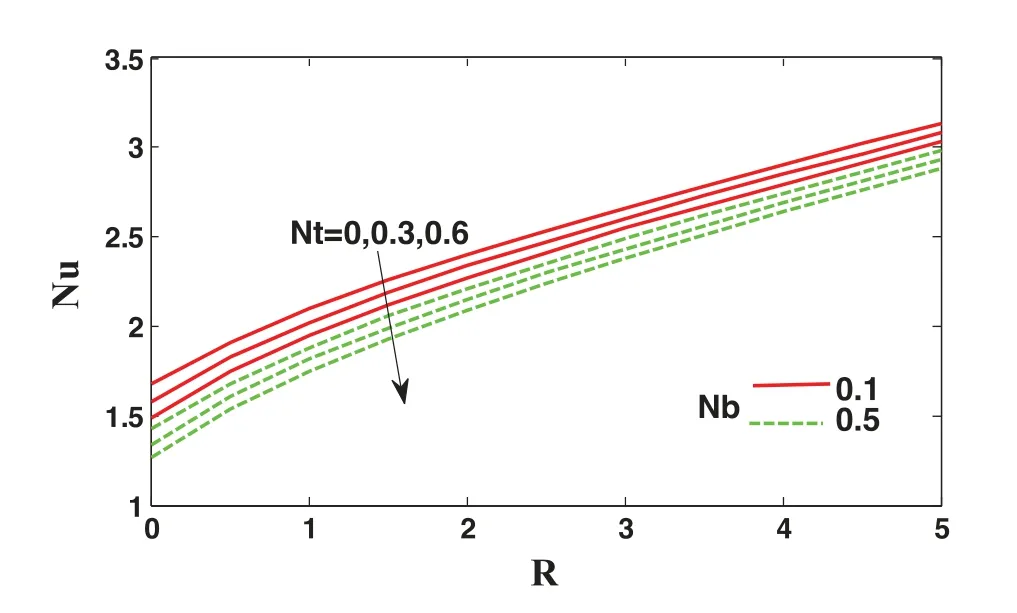
Figure 18:Effect of radiation parameter R&thermophoresis parameter Nt on local Nusselt number using Pr=1.2,∊=δ=0.1,Sc=01,M=fw=0.5,β=0.5,γ=0.01

Figure 19:Effect of magnetic parameter M on skin friction coefficient using ∊=0.1,β=0.5

Figs.20–22 show the surface plot and streamlines for velocity profile without using Maxwell fluid when the bottom wall’s velocity moves in the right and left directions.The negative sign in the captions of these figures shows that the wall is moving in the negativex-axis direction.These figures are obtained using software that uses the finite element method to solve differential equations.One side in these figures shows an inlet,and two sides are outlets.

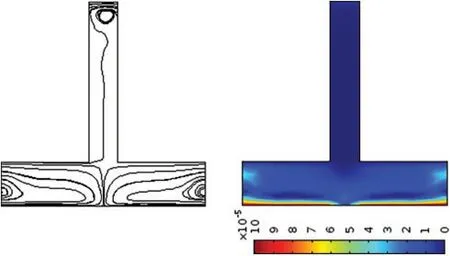
Figure 20:Surface plot and streamlines using Uw=0.0001&Uw=−0.0001

Figure 21:Surface plot and streamlines using Uw=−0.01&Uw=0.01

Figure 22:Surface plot and streamlines using Uw=−1 &Uw=1

The comparison and validation of the current study with earlier studies for determining the numerical values of the skin friction coefficient are shown in Table 1.The current methodology employs the Runge-Kutta method in conjunction with an iterative method.

Table 1:Numerical values of −f ′′(η)using M=γ=δ=fw=0

The present investigation can be useful physically to generate some experimental estimates.When the impacts of various types of fluid on solid surfaces are investigated,the effects of various parameters can be valuable in avoiding time-consuming experiments.The primary benefit of conducting a theoretical investigation is that it saves time compared to conducting experiments.

Table 2 shows the approximate ranges of some physical parameters.For practical use,any value from these ranges can be chosen.The numerical values of parameters that can be used for any practical purpose can be chosen from this Table 2.Some ranges in Table 2 depends on the length of the domain.The solution can be obtained in some smaller domains.

Table 2:Approximate numerical ranges for some parameters using Nt=0.01,Nb=0.01,M=0.01,δ=0.0,1 and ∊=0.01

Table 2 (continued)PrScβγfwR 0.01 0.01 95 0.01 ∞0.01 9∞

5 Conclusions

An existing mathematical model has been modified by considering Maxwell fluid and velocity slip boundary conditions.Moreover,the radiation and magnetic field in the unsteady flow are examined.Additionally,the effects of suction and insertion on fluid flow have been investigated.The concerning dimensional equations for the model,such as energy,momentum,and concentration equations,have been converted into non-dimensional ODEs by employing similarity transformations.In addition to this,outcomes of the variety of substantial parameters under observation on non-dimensional velocity,temperature,and concentration profiles have been delineated graphically.Summarizing all results and arguments,it is concluded that:

• The velocity profile decelerated with the escalation inM,whereas the temperature profile showed an opposite trend with suction/injection.

• Temperature,velocity,and concentration side views were seemed to decline for rising values of the unsteady parameter

• With the escalation in Maxwell,the parameterβvelocity profile tended to decrease for both suction and injection.

• Temperature profiles escalated with the escalation in Thermophoresis,and the Brownian motion parameter,Whereas,Concentration profiles seemed to decelerate for the Brownian parameter.Still,profiles showed the opposite trend for the Thermophoretic parameter.

• Due to the magnetic parameter,Mskin friction seemed to increase,whereas the heat transfer rate seemed to decrease monotonically;moreover,the heat transfer rate and skin friction inclined for the unsteady parameterδ.

• However,the heat transfer rate was escalated with an escalation in radiation parameterR.It reduced for rising values of the thermophoretic parameter.

With the escalation in Schmidt numberSc,mass transfer rate accelerated.Also,the mass transfer rate seemed to increase for the Brownian parameterNb,whereas it decreased for the thermophoretic parameterNt.Adding new effects to the model and studying the impact of various parameters on velocity,temperature,and concentration profiles analytically or numerically are possibilities in the future.

Acknowledgement:The authors wish to express their gratitude to Prince Sultan University for facilitating the publication of this article through the Theoretical and Applied Sciences Lab.

Funding Statement:The authors would like to acknowledge the support of Prince Sultan University for paying the Article Processing Charges(APC)of this publication.

Conflicts of Interest:The authors declare that they have no conflicts of interest to report regarding the present study.