水平气井斜井段气流携液分析研究

王小玮，祁丽莎，陈明珠，马文敏，姜 明，王修武*

1中国石油新疆油田公司工程技术研究院，新疆 克拉玛依

2中国石油新疆油田公司勘探开发研究院，新疆 克拉玛依

3昆明理工大学化学工程学院，云南 昆明

水平气井斜井段，持液率，临界携液，气液两相流型流态

1. 引言

水平井与直井在开采机理[1]、井身结构[2] [3]、适用条件等方面均存在较大差异，水平气井特殊的井身结构使其在斜井段能量损失较大，造成其在开采过程中易产生积液[4]，导致气井产量大幅降低[5]，甚至迫使气井停产[6]。目前普遍认为水平气井斜井段气流携液最为困难，因为斜井段气液两相流向转变剧烈、流体能量损失最为严重、最易产生积液，给实际气井稳产造成较大困扰。为此，准确预测分析水平井斜井段内的气流携液变化规律对保障气井安全生产运行至关重要[7]。

目前，国内外学者关于气井的携液机理研究主要针对直井，而对于水平气井的携液理论分析鲜有研究。携液原理方面不同学者提出了液滴运移和液膜运移两种模型[8]：液滴模型认为，液体主要以水滴的形态存在于井筒中，因此需将直径最大的液滴引至地面以排出积液；液膜模型认为液体是以液膜状的形式被夹带排出[9]。目前，尚未有学者能够将两种模型结合分析研究。

计算模型方面，江健[10]、杨功田等[11]人在Turner液滴模型的基础上纳入了倾斜角对液滴受力的影响，但在受力分析时均忽略了液滴所受曳力水平方向的分量。Gurner [12]等利用环道进行积液实验，实验倾角范围为45˚～90˚，得到的实验结果与Taitel模型[13]、Barnea模型[14]对比发现：对于垂直管道，实验结果与Taitel模型预测结果近乎一致；倾角为45˚的管道，实验结果与Barnea模型预测结果符合度更高。周兴付[15]等模拟了不同倾角下斜井段携液采气的临界气流量，修正了Keuning模型，但其缺乏理论推导和应用实践；高升[16]开展了定向气井斜井段携液模拟，发现井段倾斜角度与携液临界流量相关，并修正了适用于定向气井的携液模型，但实验未涉及气井积液过程；戚志林[17]等依据质点分析理论认为倾斜角度越大，单位临界携液流量变化越小。

可以发现，国内外关于垂直井的临界携液预测模型研究及应用较为成熟，而对水平井研究较少，忽略了水平井斜井段的特殊性，且其计算模型存在较大误差，因此有必要对水平积液气井的携液情况进行室内实验，明确水平气井斜井段携液物理模型，并根据实际气井建立可靠度较高的临界携液量计算模型，为排液采气工艺相关理论的研究做铺垫，从而保障气井安全平稳生产。

2. 实验装置及方法

2.1. 实验装置

为了研究水平井斜井段在不同实验管段倾角条件下，气水流动过程中的流型转换、持液率变化、管段积液等情况，自主设计改进了模拟气流气液两相流动状况实验装置(图1)，该装置由连续循环供水/供气系统、水平气井各井段及数据采集系统构成。井段上安有高速摄像仪、压力传感器、温度传感器、压差传感器、快速开关阀等，用以实时记录各井段内温度、压力、气体流量和液体流量等参数。实验中液相和气相分别用自来水和空气代替。

2.2. 实验参数

为修正得到精准的临界携液气量预测模型，利用上述改造的实验平台开展了斜井段不同倾角时的气水流动实验。针对实际气田的产气量、产液量范围，采用相似原理进行室内模拟实验，确定模拟实验参数如下：实验管段出口处压力为0.2 MPa和0.5 MPa，管径60 mm，倾角为10˚、15˚、30˚、45˚、60˚、74˚和90˚，液体流量分别为0.1 m3/h、0.2 m3/h、0.4 m3/h，气体流量为100 m3/h、200 m3/h、300 m3/h、400 m3/h、500 m3/h和600 m3/h (标况下)。实验通过快速开关阀控制计量实验管段中液体体积，并换算成持液率。持液率变化幅度是指两次数据之间的持液率差值与气体流量差值之比，也即是指持液率拟合曲线的二阶导数。

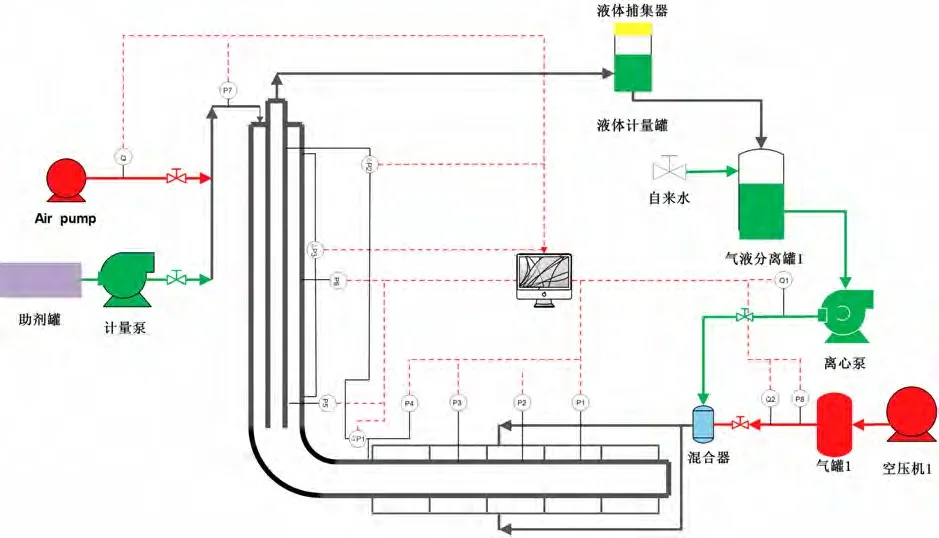
Figure 1. Experimental setup图1. 实验装置图

3. 实验分析

3.1. 实验流型

斜井段气水流动过程中，当倾角处于0˚～90˚之间变化时，气水流动规律有明显差别。通过观察实验现象发现，当倾角小于30˚且气流可以平稳携液时，管内气液两相为波状流，偶尔出现段塞流流型，如图2，图3所示。缓慢移动管段，设置倾角大于30˚时，气液两相主要以段塞流的状态呈现，如图4所示。

Figure 2. Stable liquid-carrying wave-like flow pattern of air flow at an inclination angle of 15˚图2. 倾角15˚时气流稳定携液波状流流型

Figure 3. Slug flow pattern appears when the airflow is stable and liquid-carrying at an inclination angle of 10˚图3. 倾角10˚时气流稳定携液出现段塞流流型

Figure 4. Gas-liquid two-phase flow pattern when the airflow cannot effectively carry liquid at an inclination angle of 75˚图4. 倾角75˚时气流不能有效携液时气液两相流型

气水流动实验发现：水平井斜井段内主要以层状流、段塞流及环雾状流这三种流型存在。由于实验过程中给出模拟液体流量较小，当倾角小于30˚时，气体流量越大，井筒中层状流分布形态越明显；而当倾角大于30˚时，一定液体流量、气体流量下气水两相分布主要以段塞流流型为主，且斜井段气流携液多处于段塞流向扰动流转变的临界状态。

3.2. 持液率变化

基于水平井斜井段模拟实验结果，绘制不同条件下井筒持液率的变化曲线图，分析引起持液率变化的因素。

3.2.1. 不同倾角对斜井段持液率的影响

给定产液量，变化管段倾斜角度、气体流量大小，观察分析持液率变化规律，如图5，图6所示。

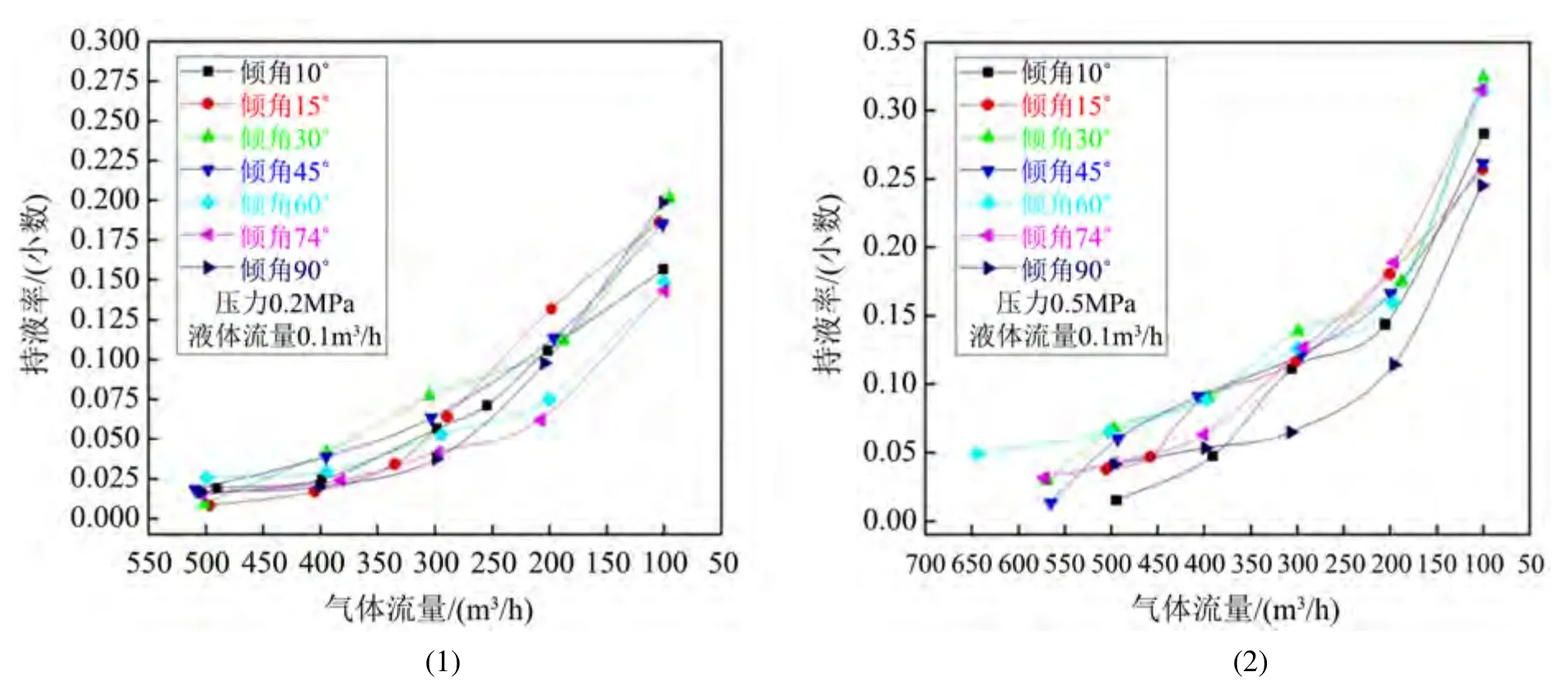
Figure 5. The change of liquid holdup rate at different inclination angles and gas flow rates at a liquid flow rate of 0.1 m3/h图5. 液体流量0.1 m3/h时不同倾角、气体流量下持液率变化

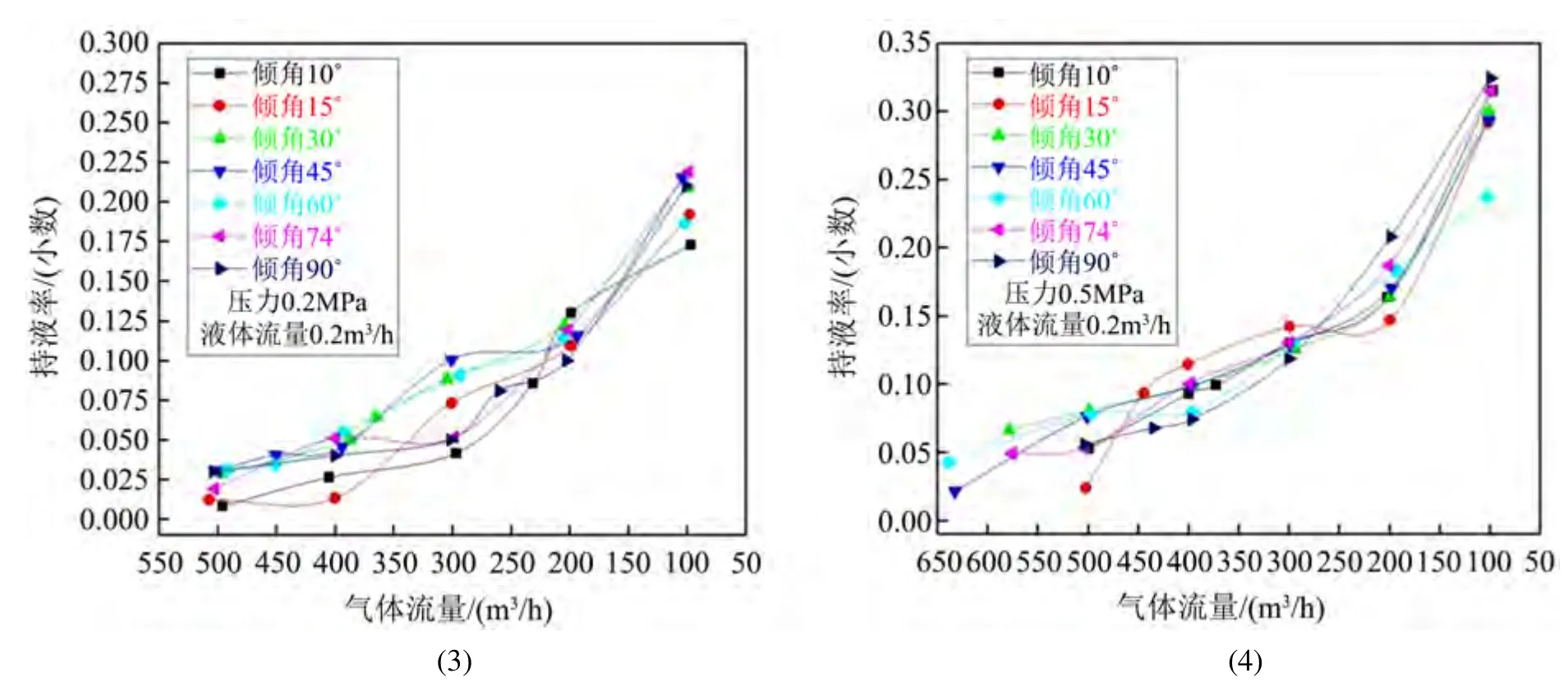
Figure 6. The change of liquid holdup rate at different inclination angles and gas flow rates at a liquid flow rate of 0.2 m3/h图6. 液体流量0.2 m3/h时不同倾角、气体流量下持液率变化

由图5、图6分析可以发现：

1) 当产气量较大时，井筒中持液率随着气体流量减小而逐渐增大；产气量较小时，井筒中持液率随着气体流量的逐渐较小而显著增加，也即井筒积液逐渐严重。

2) 由上图还可以发现，斜井段倾角程度会严重影响持液率波动情况，倾斜角度由10˚增加至45˚的过程中，持液率逐渐增大，但随着角度逐渐增大，持液率反而呈下降趋势。

3.2.2. 不同工况对斜井段持液率的影响

如图7～14绘制出了在一定倾角、不同液体流量下、持液率随气体流量变化曲线，同时标出了实验确定出的临界携液气流量(如下图中竖线所标示)。

由图7～14分析发现，当倾角一定，如为74˚时，随产气量从500 m3/h逐渐降低至50 m3/h的过程中，井筒中持液率从0.02开始不断增加，出现积液情况；其次，在试验观察得到的临界携液气体流量前后持液率与气体流量关系曲线的变化程度不同：当气体流量大于临界携液流量时，持液率随气流量缓慢变化，而当气体流量小于临界携液流量后，持液率随气流量的减小而明显增加。

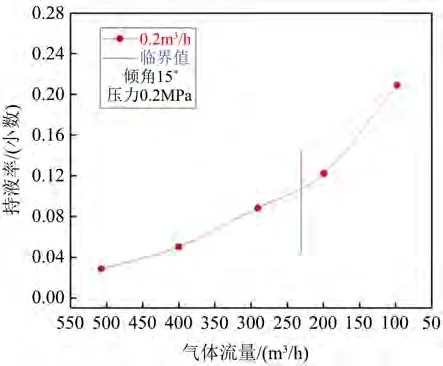
Figure 7. Change of liquid holdup when the inclination angle is 15˚ and the liquid flow rate is 0.2 m3/h图7. 倾角15˚、液体流量为0.2 m3/h时持液率变化

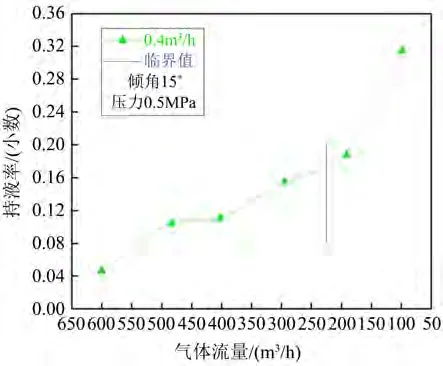
Figure 8. Change of liquid holdup when the inclination angle is 15˚ and the liquid flow rate is 0.4 m3/h图8. 倾角15˚、液体流量为0.4 m3/h时持液率变化

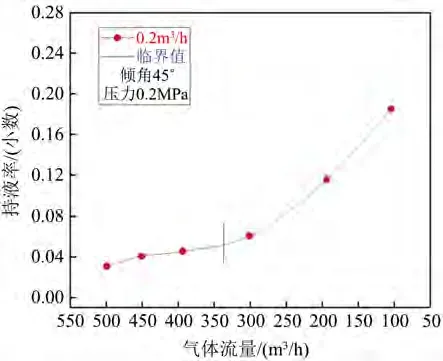
Figure 9. Change of liquid holdup when the inclination angle is 45˚ and the liquid flow rate is 0.2 m3/h图9. 倾角45˚、液体流量为0.2 m3/h时持液率变化

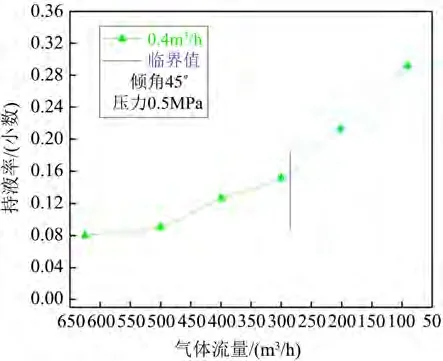
Figure 10. Change of liquid holdup when the inclination angle is 45˚ and the liquid flow rate is 0.4 m3/h图10. 倾角45˚、液体流量为0.4 m3/h时持液率变化

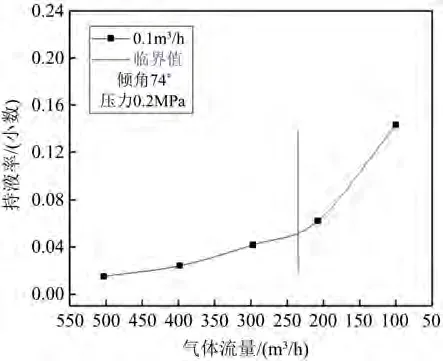
Figure 11. The change of liquid holdup when the inclination angle is 74˚ and the liquid flow rate is 0.1 m3/h图11. 倾角74˚、液体流量为0.1 m3/h时持液率变化

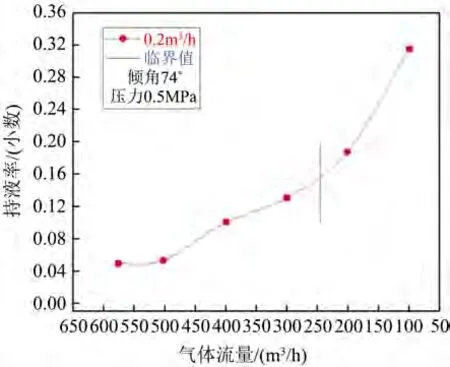
Figure 12. Change of liquid holdup when the inclination angle is 74˚ and the liquid flow rate is 0.2 m3/h图12. 倾角74˚、液体流量为0.2 m3/h时持液率变化

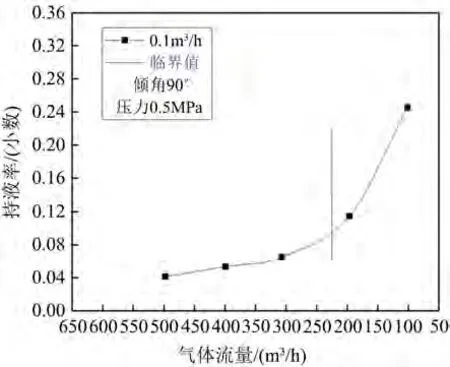
Figure 13. Change of liquid holdup when the inclination angle is 90˚ and the liquid flow rate is 0.1 m3/h图13. 倾角90˚、液体流量为0.1 m3/h时持液率变化

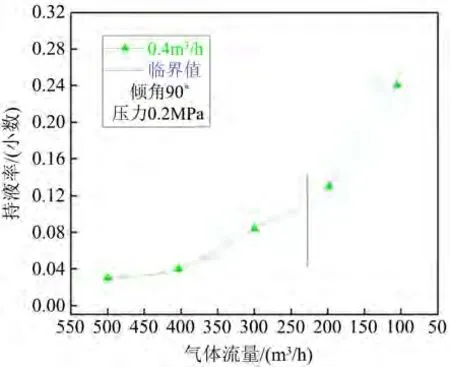
Figure 14. Change of liquid holdup when the inclination angle is 90˚ and the liquid flow rate is 0.4 m3/h图14. 倾角90˚、液体流量为0.4 m3/h时持液率变化

4. 斜井段气流携液分析

根据室内模拟实验分析可知，流体在斜井段处气液两相为段塞流或段塞流破裂成扰动流动态，因此针对斜井段临界携液模型的建立，主要以段塞流流型为物理模型。由于段塞流流型是气体流量与液体流量共同作用的结果，首先建立斜井段气液两相段塞流的持液率计算公式，然后结合单独斜井段气流临界携液状态下持液率的计算公式，联立两者进行斜井段临界模型的建立。

4.1. 斜井段气流携液时临界携液率

斜井段气流携液时气液两相呈现的段塞流流型静态实验如图15所示，以此为基础建立斜井段临界携液时持液率的计算公式。

Figure 15. Gas-liquid two-phase flow pattern in the critical state of air-carrying liquid in a 60˚ inclined well section图15. 60˚倾角斜井段气流携液临界状态时气液两相流型

斜井段段塞流模型中(如图16)，液塞的回落(图示中的LS)是引起斜井段积液的主因，液塞在液塞两端压差、气腔推动(图示中LF)、气腔中气体与液膜摩擦力、重力以及管壁之间摩擦力共同作用下倾斜向上运动。

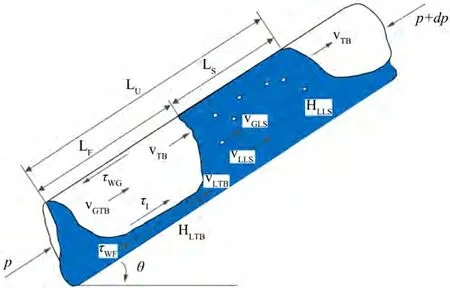
Figure 16. Schematic diagram of slug flow in inclined well section图16. 斜井段段塞流受力示意图

根据Gomez等人的研究[18]，以斜井段一个段塞单元为模型，单元中气、液体质量平衡方程为，

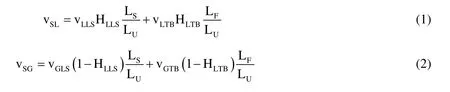
式中，vSL和vSG分别为液体和气体的表观流速，m/s；HLLS为一个物理单元内液塞中的持液率；HLTB为一个物理单元内气腔中的持液率；vLLS为液塞的真实流速，m/s；vLTB为气腔中液膜的实际流速，m/s；vGLS为液塞中气体的真实流速，m/s；vGTB为气腔的真实流速，m/s；LU为一个物理单元的长度，m；LS为一个物理单元内液塞的长度，m；LF为一个物理单元内气腔的长度，m。

同理，可以得到液塞与气腔交界面处的质量交换为，

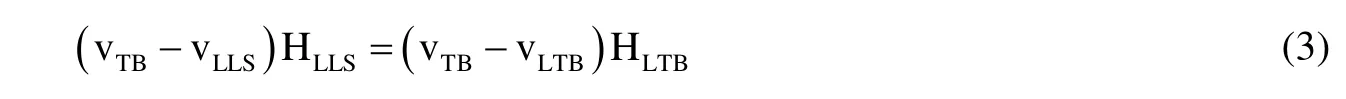
式中，vTB为段塞单元沿生产方向运动速度，m/s，根据Bendiksen等人[19]的研究，斜井段段塞流情况下vTB计算式为，

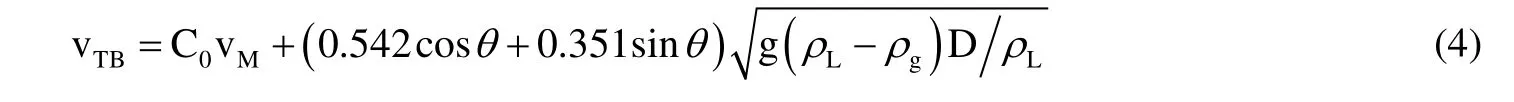
式中，参数C0的取值依赖于斜井段井斜角，根据Alves等人[20]的研究，不同井斜角下参数C0的取值分别为：1.05 (10˚～50˚)、1.15 (50˚～60˚)、1.25 (60˚～90˚)。

根据Brotz等人[21]的研究，vLTB与HLTB可以建立如下关系式，

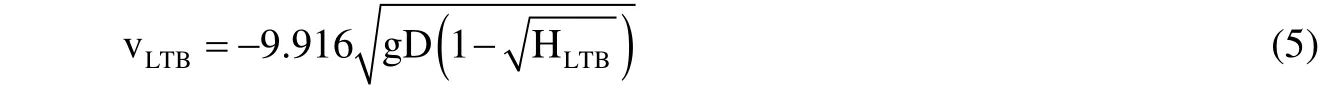
且，vGLS的计算式可用下式进行估算，

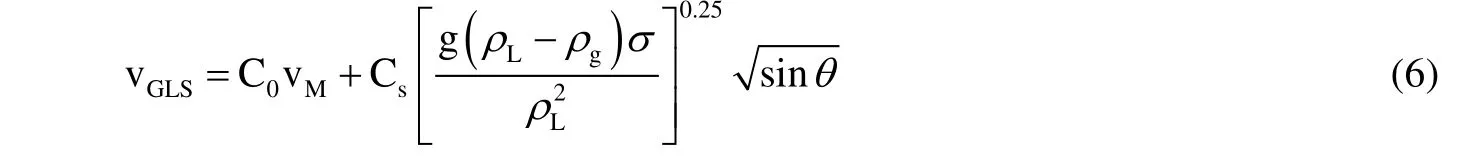
对于系数Cs的取值，可以根据Chokshi以及Tengesdal等人的研究[22]，可以取值为1.41。

根据Kaya等人[23]的研究，建立的HLLS计算表达式如下，

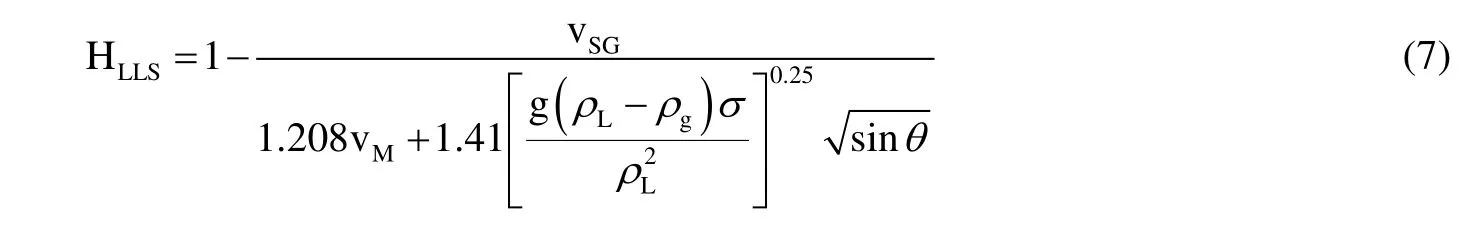
结合连续性方程，可以得到横截面处气、液各自的连续性方程为，

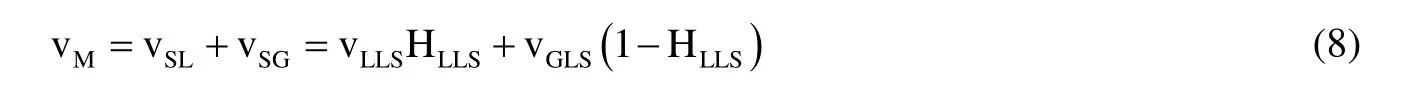
根据Gomez等人[24]的物理模型建立的持液率计算公式如下：

结合方程(3-2-2)、(3-2-3)及(3-2-9)可得，一个段塞单元内，液体持液率计算公式为，

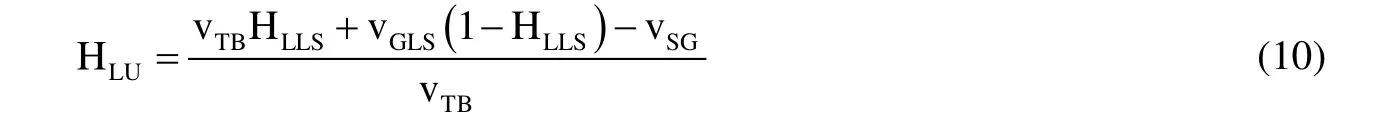
4.2. 斜井段持液率室内实验拟合

预测多相管流持液率，常用的计算方法有：Beggs-Brill方法[25]、Mukherjee-Brill [26]方法。利用室内实验对这两种方法进行分析。

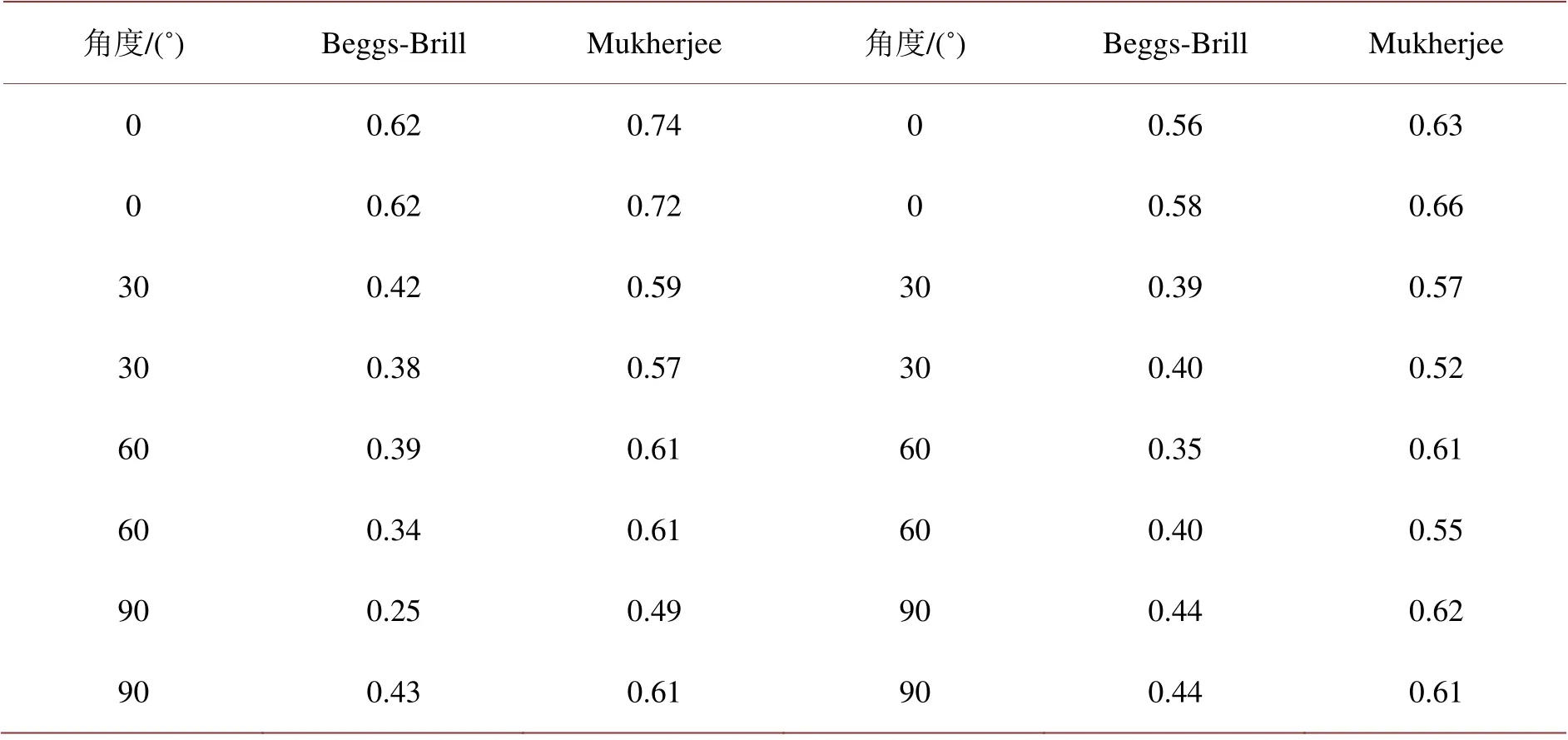
Table 1. Statistics of the prediction errors of the two methods of liquid holdup表1. 两种方法持液率预测误差统计

从表1中知，Beggs-Brill模型平均误差为0.438，Mukherjee模型其平均误差为0.607，这两种方法得到的结果差别较大。对Beggs-Brill方法和Mukherjee-Brill方法进行不同条件下持液率检验，结果如表2和表3所示。所给定的条件分别为：A. 持液率直接预测；B. 流型给出，预测持液率[27]。

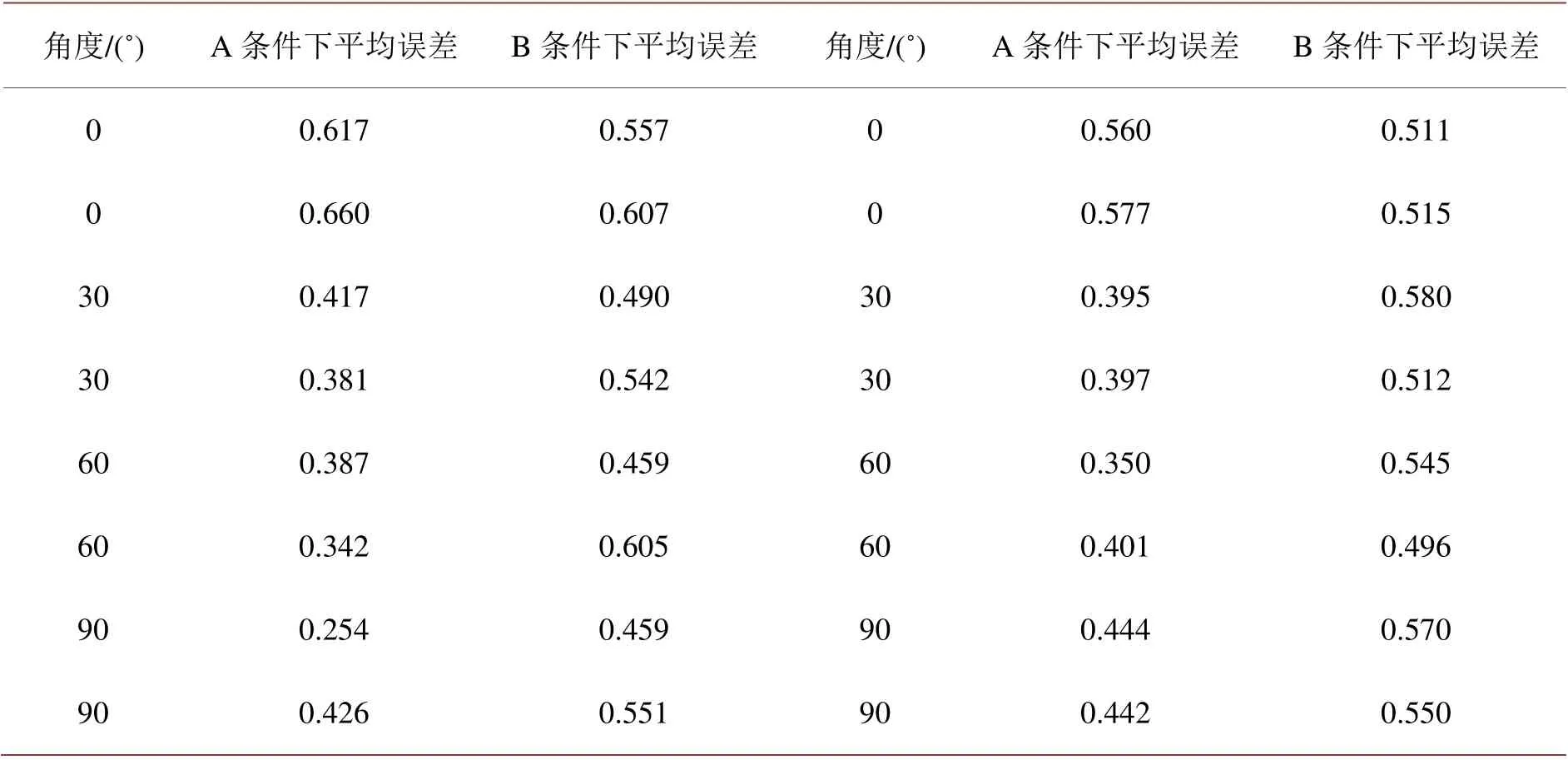
Table 2. Statistics of prediction error of liquid holdup under Beggs-Brill method A/B表2. Beggs-Brill方法A/B条件下持液率预测平均误差统计

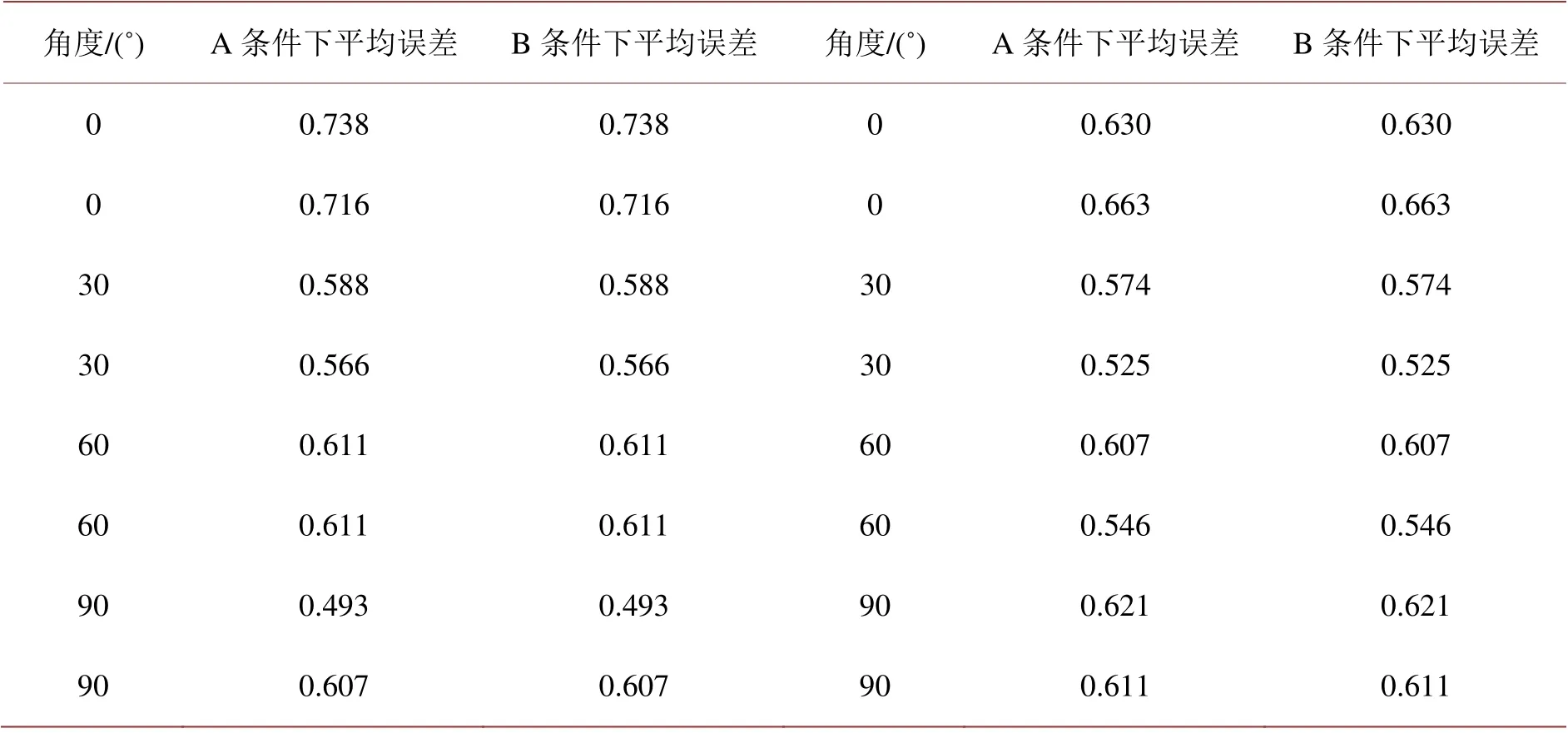
Table 3. Mukherjee-Brill method A/B liquid holdup prediction error statistics表3. Mukherjee-Brill方法A/B条件下持液率预测误差统计

由表2、表3对比可知，Beggs-Brill方法预测结果与实际相差0.1，而Mukherjee-Brill方法预测结果为与实际均为0.6067，基本吻合，因此基于单独斜井段气水两相管流系统性实验数据对Mukherjee-Brill的持液率计算方法进行重新拟合。

根据单独斜井段气水流动分析持液率结果，针对不同倾角气水流动现象及持液率等相关数据的采集，依据实际持液率变化曲线得到的不同倾角气流携液临界状态下持液率，新建临界状态下的持液率模型。

斜井状态拟合得到持液率计算公式：

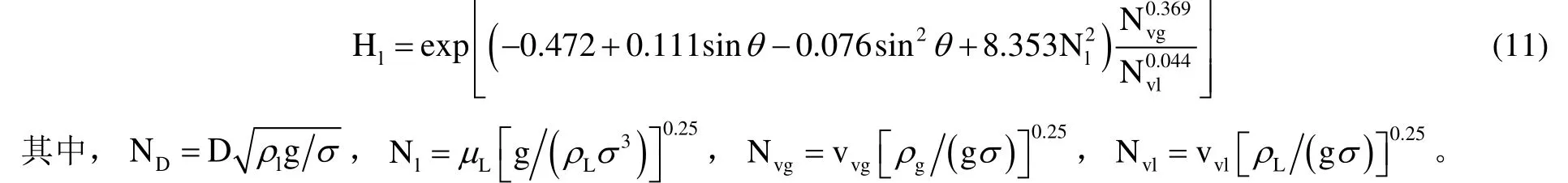
ND管道直径准数，其它参数意义均与Mukherjee-Brill方法相同。

斜井状态持液率拟合的结果如表4所示。

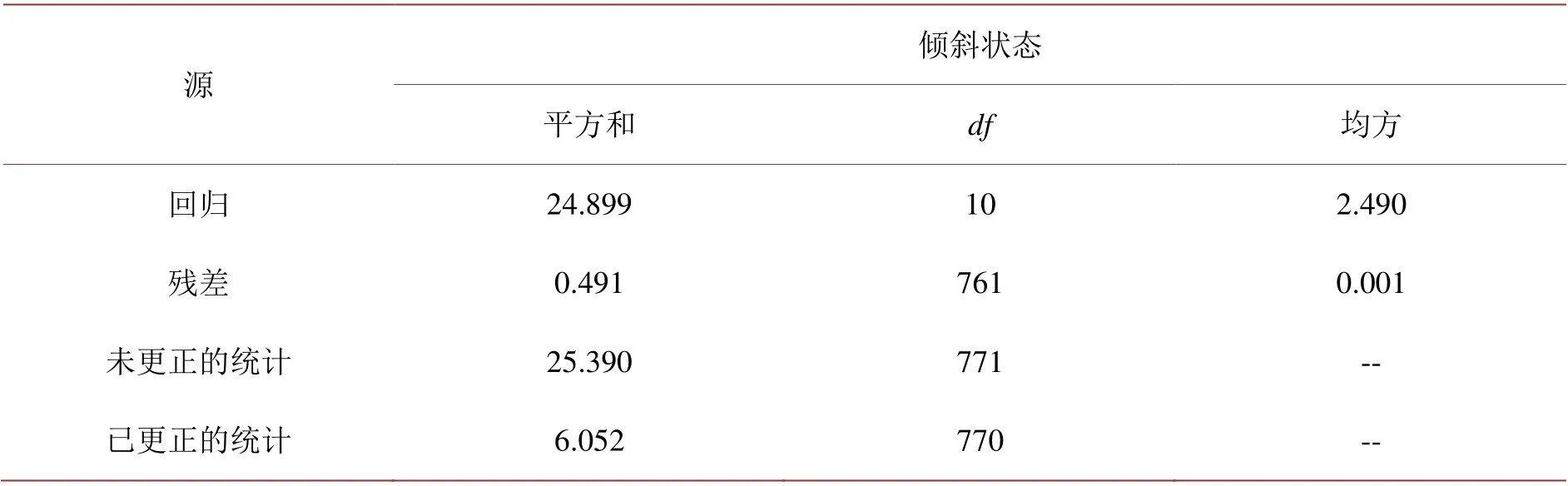
Table 4. Fitting results of inclined well section表4. 斜井段拟合结果

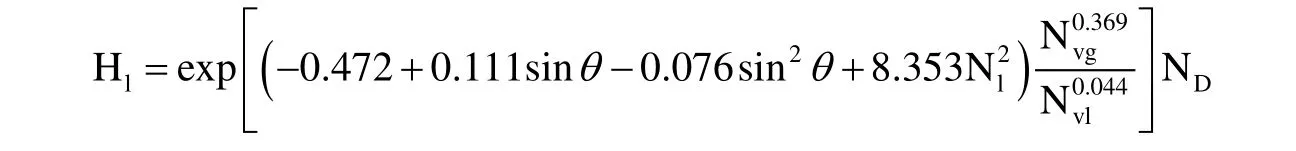
通过(1)中推导的斜井段持液率关系式与(2)中拟合的斜井段临界状态下持液率关系式，新建斜井段临界持液率状况下气流携液模型，具体如下：

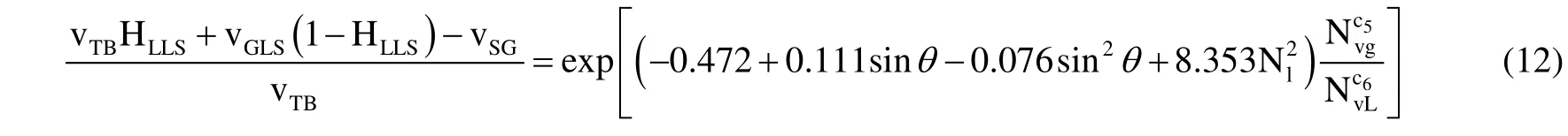
由于等式两边相关参数计算均依赖实际气体流量，故可通过试算法最终进行气体携液流量的计算。

4.3. 新模型检验

为了验证新模型的精确度和适用性，利用现场及室内实验数据，分别进行了室内验证和现场对比评价。

1) 室内模拟实验验证

根据前期的分析研究明确了斜井段为水平井最易积液井段。通过水平井单管全井筒气水流动实验，当斜井段液塞不发生回落时即认为是该工况条件下的临界状态，利用此时压力、温度及井筒中气体流量，结合建立的斜井段模型，以50˚作为斜井段气流最难带液点，进行临界携液气体流量模型的验证，对建立的数学模型进行室内模拟实验检验并完善，将实验结果与完善后的数学模型计算结果进行对比，绘制出误差图如图17所示。

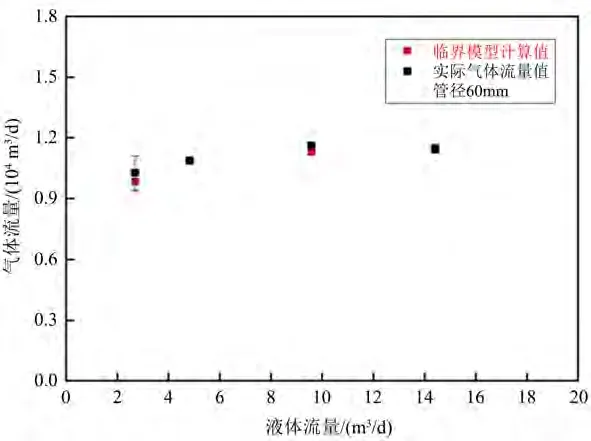
Figure 17. Comparing calculations of critical model for inclined well section图17. 斜井段临界模型计算对比

计算结果表明，建立的斜井段携液模型与室内实验结果较为吻合，经统计后平均误差为2.16%，表明建立的模型计算预测结果符合工程精度要求。

以XJ油田某一口实际水平气井为例进行计算，井身3035 m，测深3242 m，垂深3023 m，井口压力2 MPa，井口温度20℃，日产气量1 × 104m3/d，日产水量2 m3/d，井底温度104℃，油管管径62 mm，斜井段不同倾角条件下所需要的临界携液气体流量如下图18所示。

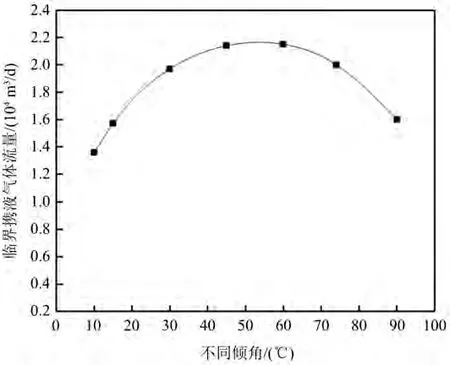
Figure 18. Critical liquid-carrying gas flow calculated under different inclination angle conditions图18. 不同倾角条件下计算的临界携液气体流量

2) 对比检验

利用实际气井测试数据对现有临界携液模型及建立的新模型进行对比，结果见下表5。

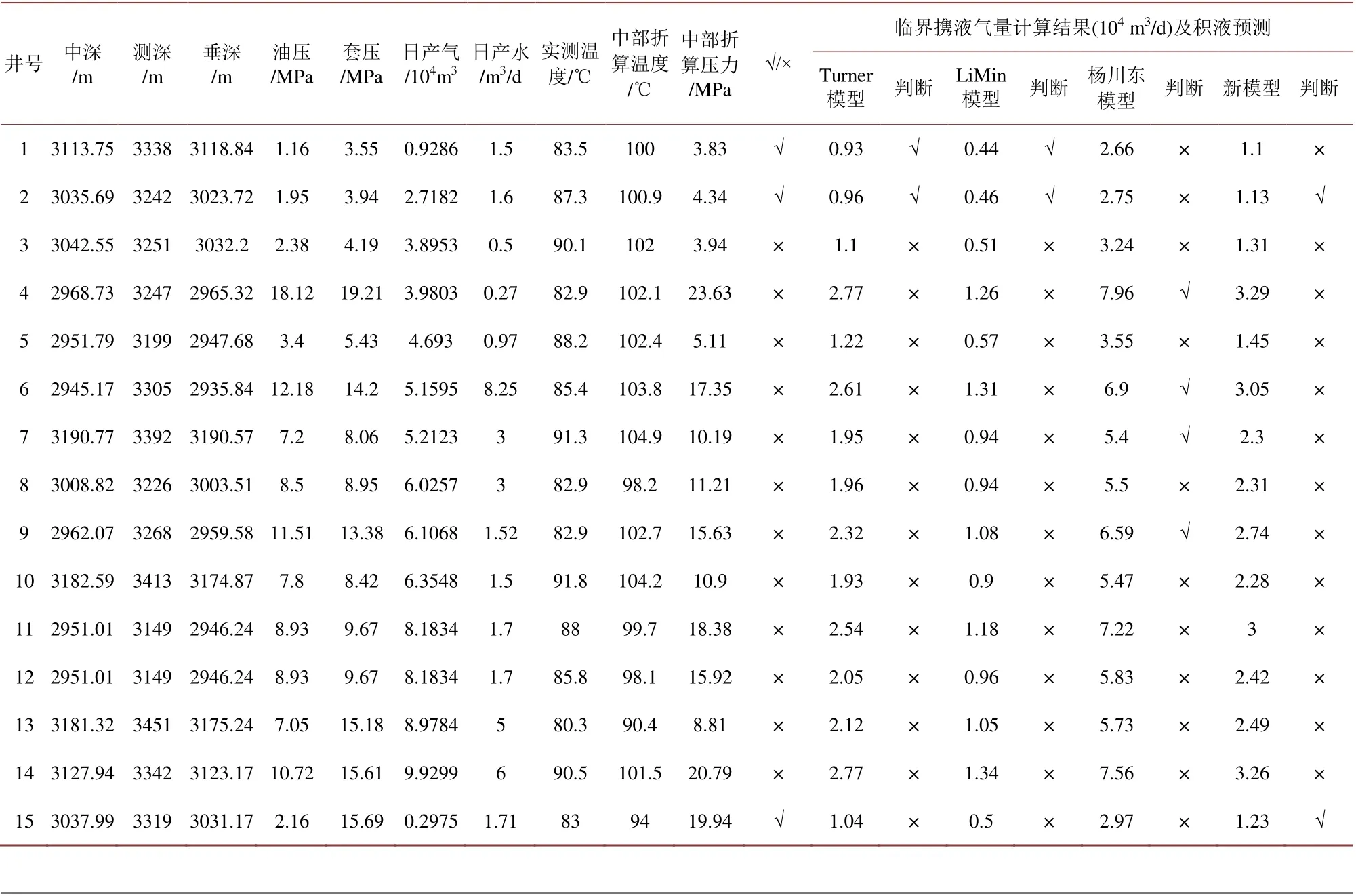
Table 5. Comparison results of measured data and model prediction data表5. 实测数据与模型预测数据对比结果

Continued

以上表格利用现场数据，与常见的临界携液流速模型进行了对比和分析，结果显示新建立的模型准确率为96%，相比Turner模型(92%)、LiMin模型(92%)、杨川东模型(60%)，其准确率更高，预测结果与实际结果吻合度更高，表明新预测模型满足工程精度要求。

5. 结论与建议

针对水平气井斜井段气液两相流流型流态及气液携液状态分析研究，得到如下结论与建议：

结论：

1) 斜井段气流携液处于段塞流向扰动流转变的临界状态，且井筒中持液率随气体流量的减小而增大，随管倾角的增大会出现波峰，呈先增大后减小的变化趋势；

2) 实际水平气井斜井段持液率的预算计算公式中，Mukherjee-Brill模型预测结果更加贴近实际，可为实际气井积液判断及排采措施实际提供一定有效数据；

3) 新建立的模型预测准确率高，平均误差为2.16%，具有较好的适用性。

建议：

通过实验和理论分析可以发现，重新拟合的临界携液新模型准确率高，对斜井段积液预测结果较好。本文的研究模拟条件及参数选取缺乏一定普适性，在以后的研究中可建立适用于不同流型的模型，进一步提高气井临界携液预测的准确性和可靠性。

基金项目

页岩气井气流携液机理数值模拟研究(项目编号：KKSQ202005031, 202001AU070087)

水平气井气水流动规律研究(项目编号：KKSY201805021)。