分时定价背景下天然气需求响应优化研究

周 军 李帅帅 梁光川 蒙 恬

1.西南石油大学石油与天然气工程学院, 四川 成都 610050;2.中国石油西南油气田公司安全环保与技术监督研究院, 四川 成都 610041

0 前言

需求响应的概念来源于电力领域,旨在运用价格杠杆引导电力用户积极参与电力需求响应,挖掘用户端负荷调节能力,保障电力供需平衡和电网安全稳定运行[1-2]。当前,天然气管网系统中还没有成功的需求响应应用经验,根据能源行业的发展趋势,在天然气管网系统中实施需求响应措施是必然的。为了解决用户用气的不均匀性,燃气供应商通常采用较传统的调度方式(如储气库等)进行调峰[3-4]。若实施天然气需求响应措施,可引导用户改变消费模式或转移用能方式,可以减少或推移高峰时段的负荷需求,降低价格波动风险,实现天然气管网系统的安全、可靠、经济运行。

需求响应的研究在电力领域已趋于成熟,李建华等人[5]指出通过有效的价格型需求响应措施,能够为用户提供价格信号,引导用户做出调整,实现电力需求负荷的削峰填谷；马骏超等人[6]考虑了经济约束条件,建立了优化峰谷电价划分时段和对应价格水平的运筹模型；苏梦[7]分析了基于电力需求价格弹性、统计学原理、消费者心理学原理等四类峰谷分时电价下用户需求响应模型的建模方法。随着能源互联网的提出和多能源系统不断地深入耦合,更多的研究集中在综合能源领域,张新鹤等人[8]考虑了天然气和电力综合需求响应,建立了天然气—电力联合峰谷分时定价的优化模型；龚凌霄等人[9]引入天然气—电力负荷综合需求响应,评估考虑需求响应的气电联合系统可靠性；许志恒等人[10]以需求响应实施手段之一的激励制度为研究对象,分析需求响应对综合能源系统运行成本和天然气网的运行影响；王伟等人[11]采用双层规划的粒子群优化算法,计算出全年最优峰谷电价和天然气价格；陈巨龙等人[12]提出了基于用户行为的分时电价时段划分和价格制定模型,以用户满意度和电网收益最大化为目标,验证了该模型的有效性；周璇等人[13]分析了英国天然气市场和容量市场的运行机制,剖析了容量市场的监管和定价模型。

随着中国能源市场的逐步放开和国家管网集团的成立,研究需求响应在天然气管网系统中的应用已成为必然趋势。本文基于价格弹性理论,建立考虑需求响应的天然气管网系统多目标运行优化模型,为天然气需求响应项目实施提供一定的理论基础。

1 价格弹性理论

天然气用户在某一时刻的需求不仅和当前时段的气价有关,也受其他时间段价格的影响,因此可以将用户对价格的响应分为单时段响应和多时段响应[14]。价格弹性是衡量需求量相对变动对价格相对变动的响应程度。以天然气需求响应为例,价格弹性系数计算见式(1)。

(1)

式中:E为价格弹性系数,体现价格变化率和需求变化率的关联;a0为初始气价,元/m3;q0为初始用气需求量,m3/h;Δq为用气需求变化量,m3/h;Δa为气价变化量,元/m3。

当某时段气价上升,天然气用户会倾向于减少该时段需求,并将其转移至相邻时段,该时段的需求减少行为称为自响应,其弹性系数称为自弹性系数,为负值;将需求转移至其他时段的行为称为互响应,其弹性系数称为交叉弹性系数,为正值[15]。自弹性系数和交叉弹性系数的计算见式(2)～(3)。

(2)

(3)

价格弹性系数矩阵见式(4)。

(4)

式中:E为价格弹性系数矩阵;T为时间集合,按照用气需求值划分为峰、平、谷时段。

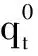
St=Bt-qtat

(5)

式中:St为天然气需求响应后用户在时段t的收益,元;Bt为天然气需求响应前用户在时段t的支出,元;qt为天然气需求响应后时段t的用气需求量,m3/h;at为天然气需求响应后时段t的气价,元/m3。

将Bt用二次函数形式描述见式(6)。

(6)

为实现用户效益最大化,需满足式(7)～(8)的条件。

(7)

(8)

用户参与天然气需求响应后第t时段的用气需求量见式(9),即为基于弹性系数的天然气需求响应的用户用气需求量。

(9)

2 天然气需求响应多目标运行优化模型

2.1 目标函数

本文在考虑峰、谷差最小的基础上,引入用户满意度,建立天然气需求响应多目标运行优化模型。

2.1.1 目标函数一

最小峰、谷差为天然气管网系统在24 h内最大需求量与最小需求量之差见式(10)。

(10)

式中:F为最大需求量与最小需求量之差,m3/h。

2.1.2 目标函数二

气费支出满意度可用来衡量气费支出的变化量大小,见式(11)；用气方式满意度的定义为天然气需求响应前、后需求之差占原需求的比值,见式(12)；用户满意度结合了气费支出满意度和用气方式满意度,以加权平均的方式表示，见式(13)。

(11)

(12)

θ=αθ1+βθ2

(13)

式中:θ1为气费支出满意度,θ1∈[0,1];θ2为用气方式满意度,θ2∈[0,1];θ为用户满意度;α为气费支出满意度权重；β为用气满意度权重；α+β=1。

对于工业用户,耗气量巨大,气费成本占总成本比例较高,为降低支出,许多工业用户会根据气价调整生产行为。而对于商业和居民用户,其用气需求主要是满足自己的舒适度,故具体的取值需根据实际用户类型占比进行分析。综上,用户满意度最大化表达式见式(14)。

(14)

2.2 约束条件

约束条件包括天然气需求响应约束、气价约束、供应方收益约束、用户收益约束,以及峰、平、谷时段划分约束等。

2.2.1 天然气需求响应约束

合理的天然气需求响应并不会影响用户的总用气量,只是将高峰时段的用气量合理地分配到其他时段,见式(15);天然气分时定价是基于价格弹性理论,故用气需求与价格的变化需满足式(16);为防止过度响应,用气需求的变化应被限制在一个合理范围内,需求允许变化范围可表示为式(17)。

(15)

(16)

(17)

式中:Q为所有时段的用气总需求量,m3/h;λmax、λmin分别为天然气需求响应前后需求量之比的上、下限。

2.2.2 气价约束

实施分时定价后,峰、平、谷时段的价格约束需要满足式(18)～(20)。

a0≤atp≤amax

(18)

amin≤atv≤a0

(19)

atv≤atf≤atp

(20)

式中:tp、tf、tv分别为峰、平、谷时段;atp、atf、atv分别为需求响应后峰、平、谷时段的气价,元/m3;amax、amin分别为气价的上、下限,元/m3。

2.2.3 供应方收益约束

天然气需求响应前供应方总收益见式(21)，天然气需求响应后供应方总收益见式(22)，供应方的利润率需在一个合理范围内,见式(23)～(24)。

(21)

(22)

(23)

rmin≤r≤rmax

(24)

式中:R0为天然气需求响应前供应方初始总收益,元;C为供应方的成本气价,元/m3;R为天然气需求响应后供应方总收益,元;r为供应方利润率;rmax、rmin分别为供应方利润率的上、下限。

2.2.4 用户收益约束

根据价格弹性系数的分析,天然气需求响应前各时段用户的收益见式(25),天然气需求响应前用户的初始总收益见式(26),天然气需求响应后用户在时段t的收益见式(27),天然气需求响应后用户总收益见式(28),天然气需求响应后的总收益必须大于天然气需求响应前总收益,用户才会响应该政策,见式(29)。

(25)

(26)

St=Bt-qtat

(27)

(28)

(29)

2.2.5 峰、平、谷时段划分约束

为避免出现天然气需求响应后峰、平、谷时段重新划分的情况,天然气需求响应后用户谷时段的最大需求值应小于平时段的最小需求值,峰时段的最小需求值应大于平时段的最大需求值,见式(30)～(31)。

(30)

(31)

式中:qtp、qtf、qtv分别为天然气需求响应后峰、平、谷时段的需求量,m3/h。

3 模型求解方法

3.1 峰、平、谷时段划分

天然气需求响应前需要对峰、平、谷时段进行划分,划分准确与否对天然气需求响应能否有效实施至关重要。峰谷价格是一项基于价格的重要天然气需求响应手段,将一天分为峰、平、谷三个时段,预先设定每个时段的气价,通过不同时段气价的差别来引导用户将部分高峰时段的需求转移至低谷时段[16-17]。本文采用K-means聚类算法对峰、平、谷时段进行划分,实现步骤有以下四步。

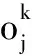
(32)

式中：xi∈Wj;ε为任意给定的正数。

3)计算3个新的聚类中心,其中mj为簇Wj中样本个数,见式(33)，聚类准则函数值φk+1见式(34)。

(33)

(34)

4)判断聚类是否合理，判断公式见式(35)。

|φk+1-φk|≤ε

(35)

若合理则迭代终止,若不合理则返回步骤2)、3)继续迭代。

3.2 多目标优化求解

本文建立一个非线性多目标运行优化模型,在现实情况下,常常出现目标函数冲突的情况,不存在一个最优设计使所有的目标同时达到最优,在这种情况下,只能求出多目标的帕累托最优解(Pareto Optim Ality)[18]。基于线性搜索过滤的原对偶内点法(Interior Point Optimizer,IPOPT)适用于求解非线性优化问题,原对偶内点法是引入障碍函数将不等式约束变成等式约束,然后采用拉格朗日乘子法进行求解,本文采用GAMS软件通过IPOPT进行求解[19-20],IPOPT求解流程见图1。

图1 IPOPT求解流程图

4 算例分析

基于所建立的天然气需求响应多目标运行优化模型,选取郑州城市燃气管网为算例,分析研究天然气需求响应对天然气管网系统的影响。

4.1 基础数据

4.1.1 用户需求

郑州市2011年6月5日24 h用户天然气需求数据[21]见表1。

表1 典型日天然气需求数据表(2011年6月5日)

4.1.2 气价及其上、下限

设当地天然气需求响应前初始气价a0为3元/m3,供应方的成本气价C为1.4元/m3;根据政府规定,天然气价格上限amax为4.5元/m3,价格下限amin为1.5元/m3,中国天然气价格弹性系数E(t,t)为-0.581。

4.1.3 时段划分

采用时段划分方法,划分结果见图2。

4.2 Pareto最优解集

Pareto最优前沿与其余可行解比较见图3,最优前沿的下方为该最优化问题的可行解,上方为不可行解,在天然气需求响应的Pareto最优解集中,因为2个目标函数相互冲突,故不可能同时达到最优情况。当最大峰谷差达到最优时,用户满意度最小,而随着最大峰谷差的增大,用户满意度越来越高,因此各个解没有优劣之别。本文选取3个结果进行分析,分别为结果1、结果5和结果10,即两侧端点和中间点。由图3可以看出,结果1是所有可行解中最大峰谷差最小的解,在满足约束条件的情况下,此时达到了天然气需求响应最大的程度;而结果10是所有可行解中满意度最大的解,此时天然气需求响应程度为0。

在所有可行解中,Pareto最优前沿上的点优于其余所有解,当用户满意度一致时,如A点与A′点,A点的最大峰谷差小于A′点最大峰谷差,即A点优于A′点;当最大峰谷差一致时,如B点与B′点,B点的用户满意度大于B′点的用户满意度,即B点优于B′点。但在Pareto最优前沿上的各点无法进行比较,如B点的用户满意度小于A点的用户满意度,但最大峰谷差也小于A点最大峰谷差,故无法评判A、B点哪一个更优。在生产实际中,需要由决策者根据实际情况进行选择,使最终结果达到相对最优。

4.3 优化结果分析

对所选取的3个结果的优化参数进行对比分析。首先分析实施天然气需求响应后用户的需求变化。

4.3.1 天然气需求响应后用户需求

天然气需求响应后用气需求见图4,结果10与天然气需求响应前的需求一致,这是因为结果10将最小化最大峰谷差的目标弱化了,以用户满意度最大为目标,由目标函数二的表达形式可以看出,当各点的需求值不变时,用户满意度达到最大为1,此时用户不参与天然气需求响应,即各时段的需求量不变。

图4 天然气需求响应后用气需求图(2011年6月5日)

4.3.2 最大峰谷差

表2为结果1、结果5和结果10的最大峰谷差。与原始需求相比,结果1的最大峰谷差较原始需求减小了11 048 m3/h,减小比例为24.7%;结果5减小了4 568 m3/h,减小比例为13.6%;结果10无变化。结果1和结果5都达到了较好的削峰填谷效果,而结果10相当于没有参与天然气需求响应,故没有削峰填谷效果。

表2 最大峰谷差表

4.3.3 分时价格

通过天然气需求响应,峰、平、谷时段的天然气价格发生了变化,结果见表3。通过天然气需求响应多目标优化,在原始气价基础上,得到了天然气需求响应后峰、平、谷的气价,且多目标不同结果下气价不同。

表3 峰、平、谷时段气价表

4.3.4 用户费用支出与供应商收益

用户根据各时段天然气价格的不同,调整自己的用气习惯。对于用户来说,各结果的当日气费支出见表4,供应商的收益见表5。从表4可以看出,结果1和结果5的用户气费支出均有减少,即参与天然气需求响应的用户会获得一定的经济效益,结果1的气费支出减少了2.3%,结果5的气费支出减少了0.8%,结果10相当于不参加需求响应,因此费用减少为无变化。

表4 用户气费支出

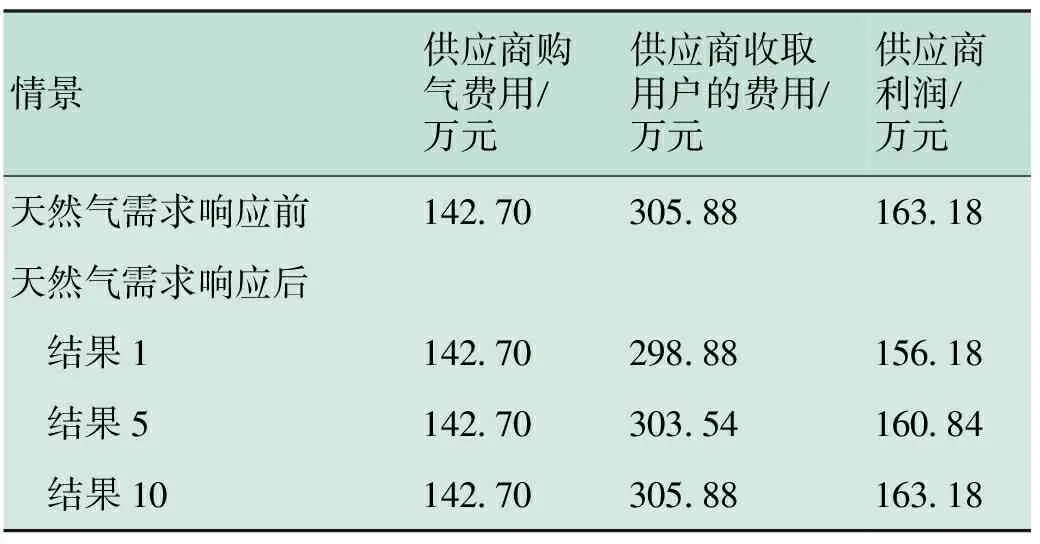
表5 供应商收益表

对于供应商来说,天然气需求响应后利润会减少,即供应商获益减少,但是在一定程度上缓解了高峰时期供气量不足,并且减缓了天然气管道及相关设备的建设费用。同时,政府机构制定了相应补贴政策来降低供应商的损失。故总体来看,天然气需求响应对供应商同样有益。多目标函数求解后得到的是Pareto最优解,即有一系列最优解,应根据实际情况选择一个最终的优化结果。为了同时保证削峰填谷效果和用户满意度,建议选择优化结果3～8作为最终决策。

5 结论

1)基于价格机制的分时定价,能够引导用户改变固有的消费模式,转移用能方式,减少或推移高峰时段的负荷需求,缓解天然气管网系统调峰压力,降低天然气管网系统供应风险。

2)天然气需求响应后可以有效降低天然气管网系统供应的最大峰谷差,达到削峰填谷效果。同时在原始气价的基础上,得到了天然气需求响应后峰、平、谷的气价,可有效指导天然气销售公司的售气价格。

3)天然气需求响应后减缓了为应对负荷高峰时期的天然气管网设施的扩建,有效降低了供应方的建设成本;同时用户用气费用支出减少,提升了用户满意度。