钢筋桁架混凝土楼板人致振动舒适度分析

卢华喜，刘美豪，吴必涛，梁平英

（1. 华东交通大学土木建筑学院，江西 南昌 330013；2. 华东交通大学轨道交通基础设施性能监测与保障国家重点实验室，江西 南昌 330013）

钢筋桁架楼承板可通过调整钢筋直径和桁架高度，实现更大的跨度和更高的承重能力，多应用于大跨度楼盖施工。 而大跨度的楼盖体系在反复的环境振动特别是人行荷载作用下，易产生较大的竖向振动，容易给结构舒适度造成不利影响。

随着生活质量的提高，居民对环境舒适度的要求也越来越高，楼板结构的振动舒适度问题也引发了更多的关注。 此前，有不少学者做过关于楼板振动舒适度方面的研究。 在国外，Lee 等[1]通过现场振动测量试验，对韩国钢结构建筑TechnoMart 发生的异常振动事故原因进行了调查，发现楼盖体系的基频过低 （仅为2.7 Hz）， 是引起异常振动的主要原因。 Varela 等[2]通过试验研究了组合楼板的人致振动问题，分析了人行轨迹、随机性和人数等因素的影响。 在国内，《组合楼板设计与施工规范》（CECS 273-2010）、《高层建筑混凝土结构技术规程》（JGJ 3-2010）等规范规程，也对混凝土楼盖舒适度方面的限值作了规定。 屈文俊等[3-4]通过有限元瞬态动力分析对压型钢板-混凝土组合楼盖体系进行舒适度评价，并提出了满足舒适度要求的板厚建议公式。 张坤[5]对中科院巨型钢框架悬挂结构体系楼板开展了舒适度评价， 通过人致激励试验， 研究了人数、步频、行走路线等因素对楼板振动的响应规律。 李守继等[6]，何余良等[7]采用数值模拟或现场振动试验对装配式叠合楼板体系进行了人行激励下的振动舒适度研究。

钢筋桁架楼承板因其整体性好、 节省模板、工业化程度高等优势， 越来越多地被应用于高层、超高层钢结构中。 然而目前国内针对钢筋桁架楼承板振动舒适度方面的研究还不够充分[8-9]，缺乏针对钢筋桁架楼承板-混凝土双向板振动舒适度方面的研究。 钢筋桁架楼承板主要由钢筋桁架、底部钢板组成。 钢筋桁架高度、底部钢板的改变对楼板刚度有较大的影响[10]，必然会影响楼板的振动舒适度。本文基于钢筋桁架混凝土单向板简谐激励下动力性能测试试验， 对钢筋桁架混凝土板ANSYS 动力分析模型进行了校验。 建立了人致激励下钢筋桁架混凝土双向板动力分析模型，分析了板厚、底部钢板对楼板振动性能及舒适度的影响，并与同等规格的开口型压型钢板-混凝土组合楼板（简称“组合楼板”）进行对比分析，为钢筋桁架楼混凝土楼板的振动舒适度设计提供参考。

1 楼板简谐激励振动试验

1.1 试件设计

本次试验以两块钢筋桁架混凝土单向板为实验对象， 两块试件尺寸参数见表1。 选用TD2-70-600、TD3-90-600 两块钢筋桁架楼承板， 其底板均采用Q235 冷轧钢板，厚度为0.5 mm，钢筋桁架楼承板参数见表2， 上、 下弦钢筋采用HRB400 级钢筋， 腹杆钢筋采用HPB300 级钢筋。 试件采用C30商品混凝土放置于地面直接浇筑，试件横截面如图1 所示。

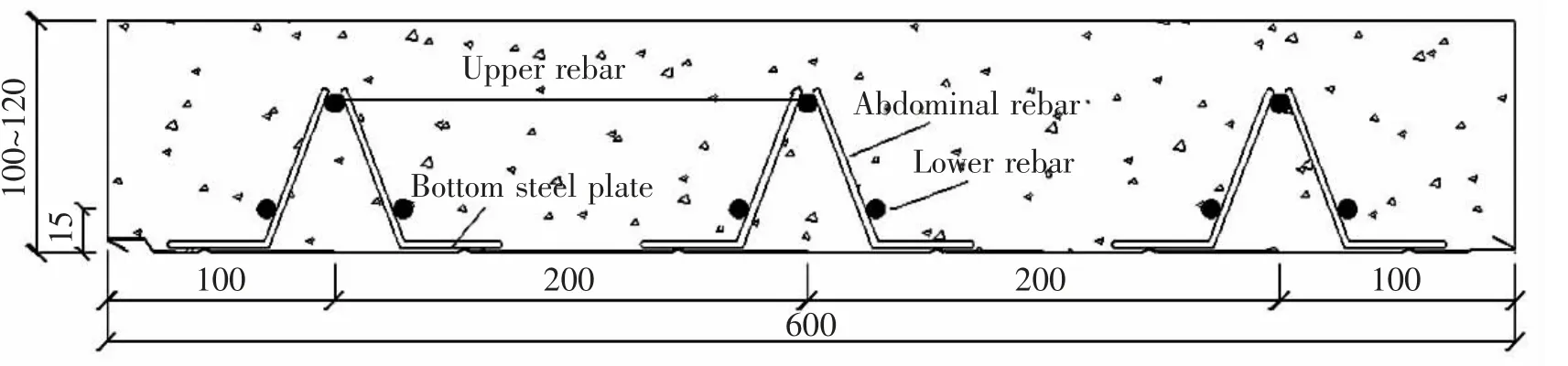
图1 楼板试件截面图（单位：mm）Fig.1 Cross-section view of floor specimen (Unit: mm)

表1 钢筋桁架混凝土楼板参数Tab.1 Parameters of steel truss concrete floor

表2 钢筋桁架楼承板参数Tab.2 Parameters of reinforced truss floor deck mm

1.2 试验方案及测点布置

在测试钢筋桁架混凝土单向板振动响应时，楼板两端简支于钢梁上，使用TST 动静态信号测试分析系统测试楼板的振动响应。 在板面中线位置等距布置5 个加速度传感器以拾取楼板的振动加速度时程，其测点布置见图2 所示。

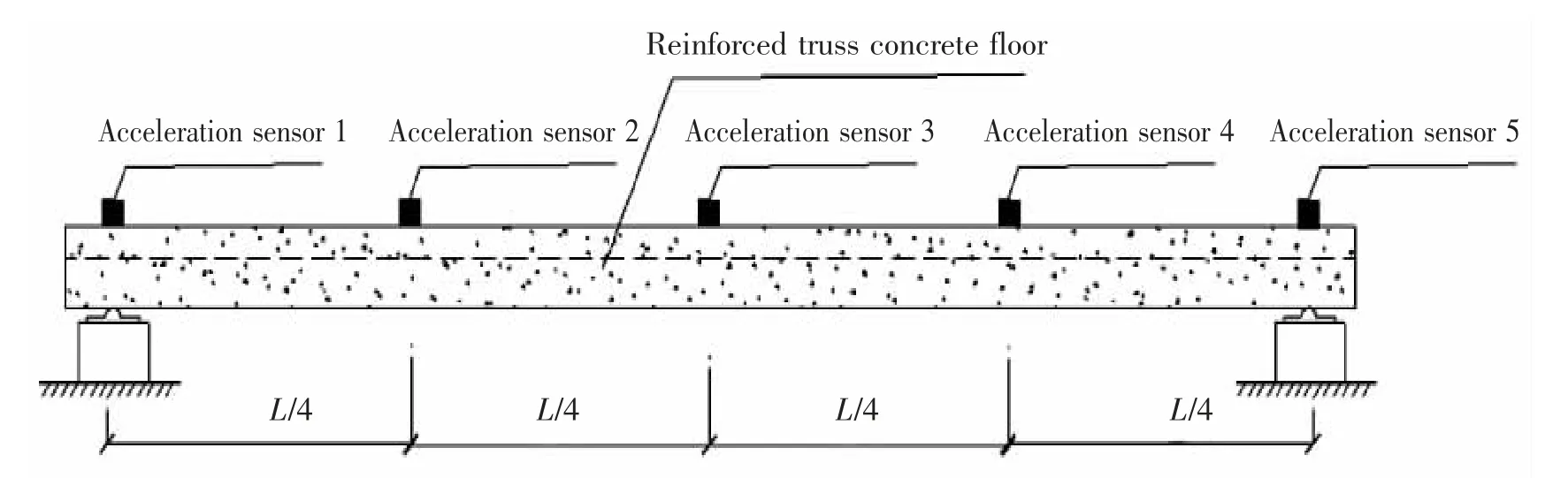
图2 动力分析试验传感器布置图Fig.2 Layout of dynamic analysis test sensor

为了实验的准确性，本次试验设置锤击和电动式激振器激励两种激励方式和多种荷载工况，见表3。其中，锤击激励是为了准确地获取楼板的模态情况，电动式激振器激励是为了获取楼板在持续简谐（正弦）荷载作用下的振动性能，每种工况下持续采集30 s。

表3 激励工况Tab.3 Incentive conditions

设备调试完毕后， 利用激励锤在板面上锤击，使楼板进行衰减振动，通过加速度传感器采集5 个测点的加速度时域信号并传输到计算机，每块楼板重复测试3 次，并对测试结果进行分析；而后通过信号发生器生成稳定的简谐（正弦）波，偏移和相位均为零。 经功率放大器推动电动式激振器在楼板上进行持续振动，采集各工况下钢筋桁架楼板的振动响应。

1.3 结果分析

对锤击激励采集的加速度时域信号经过FFT傅立叶变换得到其加速度频谱，通过加速度频谱可得到B1 和B2 楼板的基频分别为52.53 Hz 和60.75 Hz。结果表明，增加钢筋桁架混凝土楼板的厚度对自振频率有明显的提升。

经过测试得到各测点的加速度响应。 经对比分析发现，于楼板中央位置激振时，钢筋桁架混凝土楼板的振动峰值加速度均出现在测点3（楼板中央），取测点3 的楼板加速度峰值进行分析，各工况下测点3 加速度峰值变化情况如表4 所示。

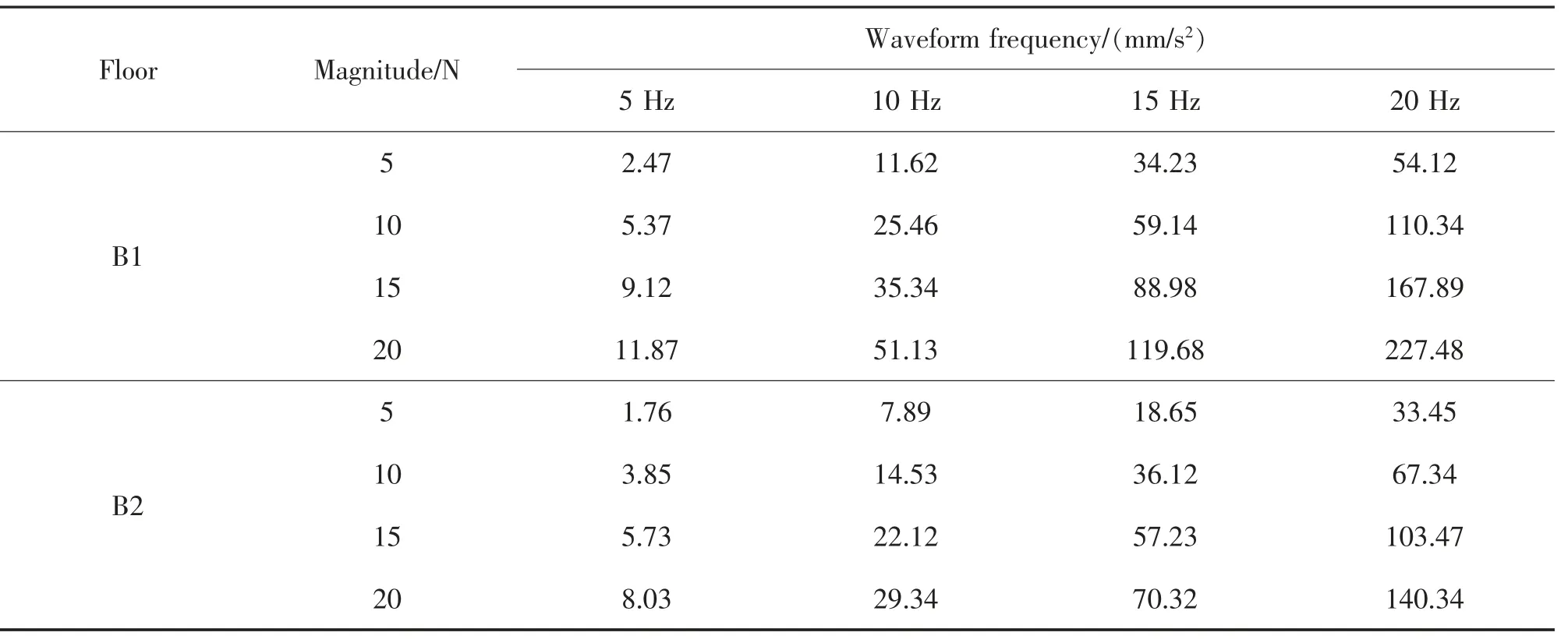
表4 钢筋桁架混凝土楼板激振加速度幅值Tab.4 Acceleration amplitude of reinforced concrete slab excitation

试验数据表明， 在小幅值的简谐荷载持续作用下，试件处于弹性阶段，钢筋桁架混凝土单向板的加速度峰值与激振幅值呈线性关系。 随着波形频率的逐渐增大， 简谐激振响应加速度的增大幅度越来越大， 且在相同激振幅值下，B2 板的加速度峰值相较于B1 板平均减小了38.62%。 由此可知， 增大楼板的厚度可显著减小其受动力作用下的振动加速度。

2 有限元分析

2.1 模型的建立

一些学者指出，在进行动力分析时,混凝土的弹性模量会适当的提高， 故在进行楼板的动力分析时，取混凝土的弹性模量为实测值的1.35 倍[11-12]。基于表5 的楼板材料属性,使用ANSYS 有限元软件建立两块楼板试件的三维实体模型，并模拟楼板与钢梁之间的简支边界条件。 其中，混凝土采用Solid65实体单元模拟，钢筋采用Link8 杆单元模拟，底板采用SHELL181 壳单元模拟， 有限元网格划分为50 mm。由于本次试验中，楼板所承受的激励相对较小，材料处于弹性阶段，可将钢材和混凝土考虑为弹性材料，且混凝土、钢筋和底部钢板3 者之间不会出现滑移，故可采用共享节点的方式建立3 者之间的共同受力[4]。 楼板有限元模型如图3 所示。

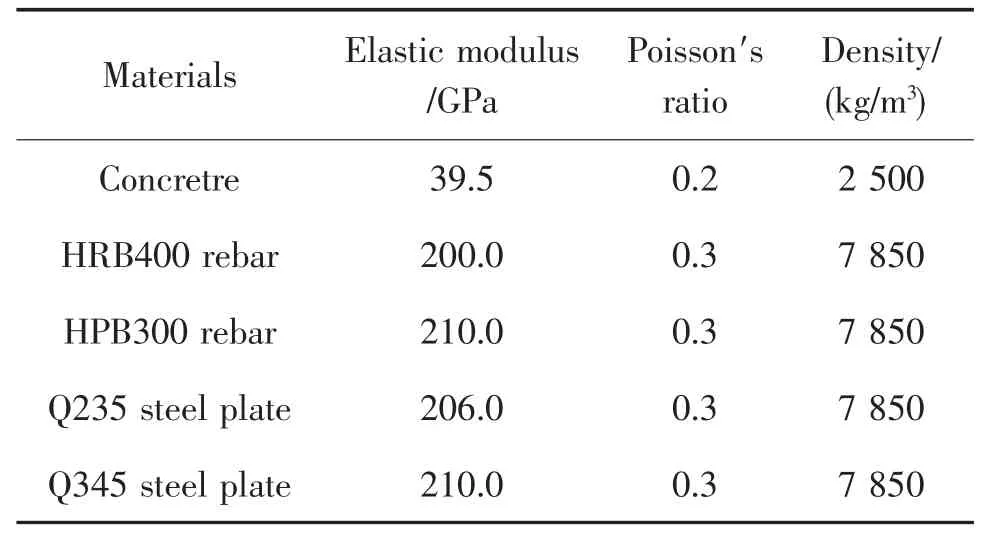
表5 钢筋桁架混凝土楼板的材料属性Tab.5 Material properties of reinforced concrete slab truss

图3 楼板有限元模型Fig.3 Finite element model of floor

2.2 对比分析

在进行动力分析时，楼盖体系在基频时能量最大，第1 阶频率是最重要的，在进行模态分析时可主要考虑楼板竖向振动的第1 阶自振频率[13]。 通过试验和有限元方法分别对B1 和B2 板进行模态分析，由表6 对比结果可知：针对钢筋桁架混凝土楼板的模态分析，使用有限元方法可以得到与实验值较吻合的结果，1 阶自振频率模拟值与实测值的误差在4%左右， 使用有限元方法对钢筋桁架混凝土楼板进行模态分析可以得到可靠的结果。

表6 楼板自振频率试验值与模拟值对比Tab.6 Comparison between test value and simulation value of natural frequency of floor

在楼板模型的中央节点施加一定幅值和频率的正弦激励以模拟电动式激振器对楼板的激励作用，得到简谐荷载幅值为10 N 和20 N 作用下，楼板中央节点的加速度峰值随频率变化的结果与试验数值对比情况如图4～图5 所示。

图4 激振幅值10 N 时楼板振动加速度Fig.4 Floor vibration acceleration at the excitation amplitude value of 10 N

图5 激振幅值20 N 时楼板加速度峰值Fig.5 Peak floor acceleration at the excitation amplitude value of 20 N

经图4～图5 对比可知， 随着激振频率的增加，两块试件振动加速度峰值的模拟值与实测值曲线走势基本相同，模拟值较试验值稍大，但两者误差在合理的范围内， 说明ANSYS 有限元分析软件能够较准确地模拟动力荷载激励下钢筋桁架混凝土楼板的振动特性，由此验证了文中钢筋桁架混凝土楼板建模方法的正确性。

3 楼板人致振动舒适度分析

3.1 人行激励模型

假设人行走过程中脚步产生的动力荷载由单步荷载所产生的脉冲序列叠加模拟出来。 在设定的步频下，可认为行走荷载是完全周期性的。 人行走产生的竖向激励通常用傅立叶级数来表示

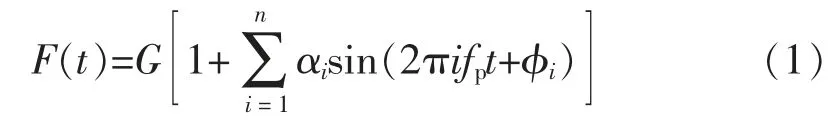
式中：G 为人的体重，根据相关规范，取为700 N；αi为第i 阶的荷载动力因子 （DLFs），Gαi即表示动力荷载组成部分的大小；fp表示人步行频率， 本文取1.6 Hz；ϕi为第i 阶荷载的相位角， 前4 阶分别取ϕ1=0，ϕ2=-π/2，ϕ3=π，ϕ4=π/2；n 为荷载的总谐波数，取前4 阶。

采用人行荷载定点加载方法对楼板进行激励[14]。对于式（1），最重要的是确定其动力荷载因子，本文根据Smith[15]等总结的傅立叶连续荷载模型DLFs 取值：α1=0.436 （fp-0.95），α2=0.006 （2 fp+12.3），α3=0.007（3 fp+5.2），α4=0.007（4 fp+2.0）。

3.2 楼板计算模型选取及模型建立

为了研究钢筋桁架混凝土双向板的振动特性以及人行荷载作用下的振动舒适度问题， 采用ANSYS 有限元软件分别计算多组不同厚度的钢筋桁架混凝土楼板的振动响应， 并考虑底板对振动的影响， 再与同样在钢结构中应用广泛的开口型组合楼板作对比分析。 选取4 块钢筋桁架混凝土楼板和4块开口型组合楼板进行分析， 楼板型号及规格见表7。选用算例为单层单跨的H 型钢梁-RHS框架结构体系，楼板布置情况如图6 所示。 其中钢筋桁架混凝土楼板长度方向为12 块底板宽度为600 mm 的TD4 钢筋桁架楼承板拼接而成， 宽度为钢筋桁架楼承板的单块板跨度。 楼板沿着垂直于上下弦钢筋方向配置Ф8@100 mm 的HRB400 分布钢筋以增加楼板整体性，TD4 钢筋桁架楼承板参数见表8。 开口型组合楼板底板均采用12 块型号为YX75-200-600 压型钢板拼接而成， 单块开口型压型钢板截面如图7 所示。两种楼板均采用C30混凝土浇筑， 其中YX75-200-600 压型钢板采用Q345 钢。

图6 单跨框架平面布置图（单位：mm）Fig.6 Layout plan of single-span frame (Unit: mm)

表7 楼板型号及尺寸参数Tab.7 Floor model and size parameter

表8 TD4 钢筋桁架楼承板型号参数Tab.8 TD4 reinforced truss floor deck model parameter mm

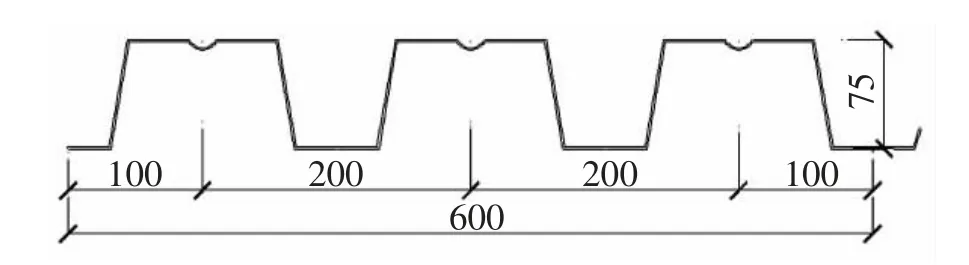
图7 YX75-200-600 压型钢板截面图（单位：mm）Fig.7 Sectional view of YX75-200-600 profiled steel plate(Unit:mm)

基于表7 中所选用的楼板规格及材料属性,使用ANSYS 有限元软件对其进行建模分析， 钢板采用SHELL181 单元，钢筋采用Link8 单元，混凝土采用Solid65 单元，并合理划分模型网格大小。 由于研究的是双向楼板的振动舒适度问题，所以在建模时没有考虑上下层整体结构刚度对楼板的影响，只选取了某层楼板进行研究。 考虑实际工程中钢筋桁架楼承板和组合楼板与钢梁之间采用栓钉连接，承受弯矩能力较弱， 建模时限制楼板四周结点x，y，z 3个方向的平动约束， 准确模拟楼板的实际约束情况。HJB-1 和YXB-1 的有限元模型如图8 所示。

图8 HJB-1 和YXB-1 的有限元模型Fig.8 Finite element models of HJB-1 and YXB-1

使用瞬态动力分析模拟人行荷载下楼板的振动响应时，由于人行荷载较小，楼板在未出现较多裂缝之前符合平截面假定， 可认为两种楼板均处于弹性小变形范围，混凝土、钢筋和底部钢板3 者之间不会出现滑移， 故在对两种类型楼板的建模中均采用共享节点的方式模拟混凝土与钢板之间的接触[4]。 考虑到现实中楼面非结构构件的影响，楼板结构的阻尼比一般处于0.02～0.12，高于楼板结构承载力计算时所取的阻尼比，文中出于保守考虑，取0.02[16]。

3.3 结果分析

3.3.1 振动特性

对选用的钢筋桁架混凝土楼板和组合楼板进行模态分析，使用分块兰索斯法（Block Lanczos）提取楼板的模态情况。 前3 阶自振频率见表9 所列。

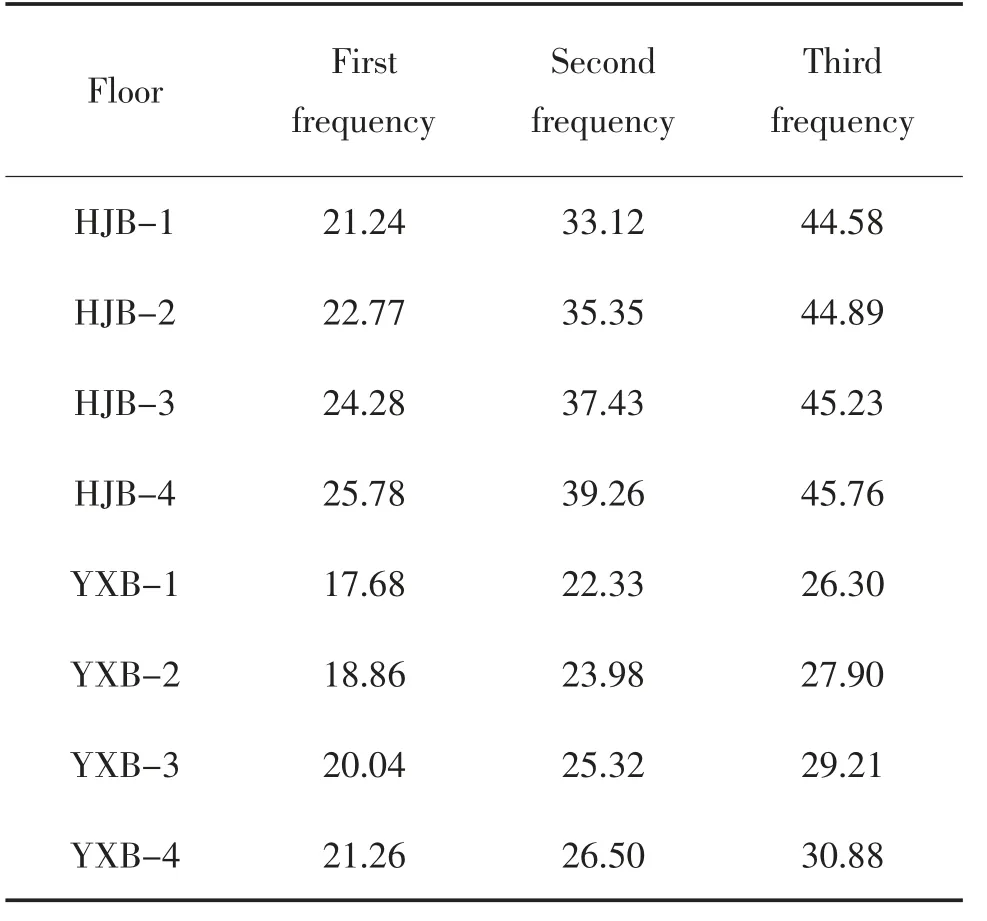
表9 不同型号楼板的自振频率Tab.9 Natural vibration frequencies of different types of floors Hz

结果表明，相同约束情况下钢筋桁架混凝土楼板的基频较组合楼板平均高20.14%。楼板结构自振频率越低，越容易在人群活动时引发共振从而诱发振动舒适度问题。 实际工程中可通过减小次梁间距或增强楼板四周约束以增加楼板结构的自振频率，从而达到改善楼盖体系振动舒适度的目的。 HJB-1和YXB-1 的前3 阶振型对比如图9 所示， 均为竖向振动，两种楼板的第1 阶振型位移最大点均出现在楼板中央位置。

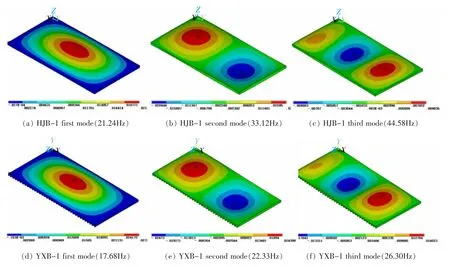
图9 HJB-1 和YXB-1 的前三阶振型图Fig.9 The first three modes of HJB-1 and YXB-1

模态分析表明，楼板振动时，其位移和加速度最不利位置均出现在楼板中央。 将式（1）得到的人行激励加载到楼板第1 阶振型位移最大值处的节点，设置行走频率，以模拟人在楼板中央原地踏步的情景。 由ANSYS 瞬态动力分析得到HJB-1 和YXB-1 的加速度时程曲线如图10 所示，HJB-1 和YXB-1 的加速度峰值分别为0.059 1m/s2，0.097 9 m/s2，且在人行激励下，两种楼板的加速度峰值均出现于第一步加载时刻，第一步过后楼板的加速度峰值出现小幅度衰减，而后随着人行走状态的稳定加速度峰值趋于稳定直至加载结束。 相同激励条件下，HJB-1 振动加速度峰值比YXB-1 小65.65%， 钢筋桁架混凝土楼板的振动舒适度优于同等厚度的开口型组合楼板，这是因为开口型压型钢板由于底部凹肋的存在相较于等厚钢筋桁架混凝土楼板质量、刚度均更低，给其振动舒适度造成了不利影响。

图10 HJB-1 和YXB-1 的加速度时程曲线Fig.10 Acceleration time history curves of HJB-1 and YXB-1

3.3.2 底板的影响

随着技术的不断更新， 近些年推出了一种可拆卸底板的钢筋桁架楼承板，由于实际工程中，一般不考虑钢筋桁架楼承板底部压型钢板参与组合，底部压型钢板只充当施工时的模板使用，故较少考虑拆卸底板给楼板造成的影响。 而一些研究发现钢筋桁架楼承板底部模板的存在对楼板的整体刚度有较明显的影响[12]，改变底板的厚度或者在混凝土达到强度后拆除底板势必会影响楼板的整体刚度，从而给楼板振动舒适度造成不利影响。 考虑到工程中常用的楼承板底板厚度为0.5～0.8 mm，本文分别对0.5，0.8 mm 和拆除底板的钢筋桁架混凝土楼板进行人行激励下的瞬态动力分析。 不同底板厚度的楼板自振频率和加速度峰值曲线如图11 所示。

图11 底板对楼板振动响应的影响Fig.11 The influence of the slab on the vibration response of the floor

由图11 可知，拆除底板后，钢筋桁架混凝土楼板的自振频率降低了4.37%， 加速度峰值增加了19.76%。 且模板厚度也一定程度上影响了楼板的振动舒适度。 针对振动舒适度要求高或者对环境振动较敏感的建筑物，在进行钢筋桁架楼承板施工时建议保留底板。

3.3.3 楼板厚度的影响

钢筋桁架混凝土楼板由钢筋桁架、 底部钢板和混凝土多种材料组成， 标准的钢筋桁架混凝土楼板厚度为在钢筋桁架高度的基础上加30 mm。当增加楼板的厚度时，钢筋桁架、腹杆钢筋高度也随之增加，对楼板的质量和刚度均有较大影响。 分别分析了不同厚度的钢筋桁架混凝土楼板和开口型组合楼板人致激励下的振动响应，HJB 和YXB 的自振频率和加速度峰值随厚度的变化情况如图12所示。

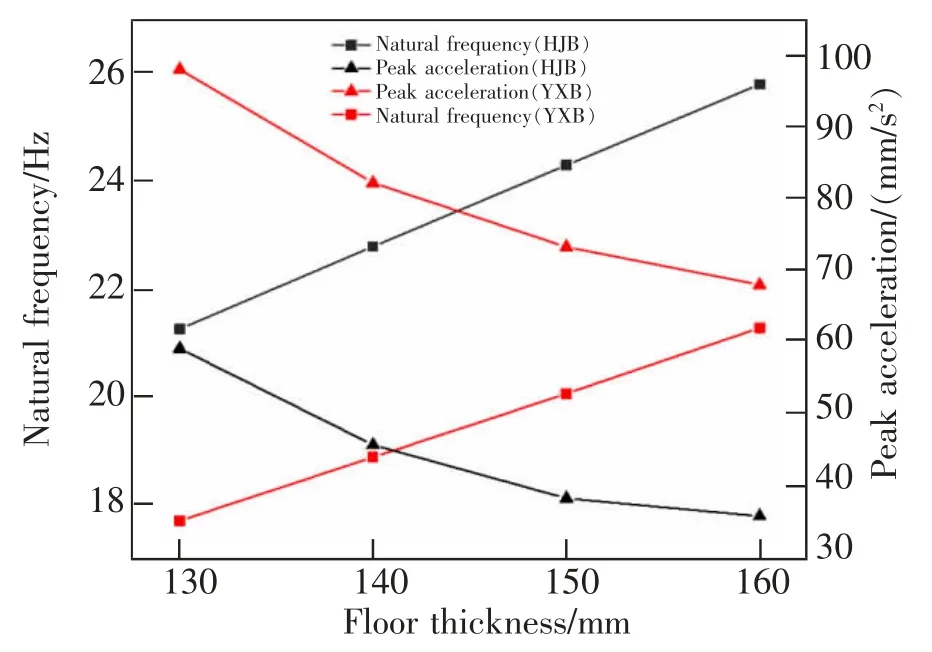
图12 楼板厚度对楼板振动响应的影响Fig.12 The influence of floor slab thickness on floor slab vibration response

由图12 可知，HJB 和YXB 的自振频率和振动加速度峰值随楼板厚度的变化趋势基本相同，HJB和YXB 的自振频率随着厚度从130 mm 增加到160 mm，分别增加了21.37%和20.25%，相应的振动加速度峰值分别减少了39.49%和30.64%。 两种楼板的自振频率随着楼板厚度的增加，接近于线性增长， 而加速度峰值随着楼板厚度的增加变化的趋势在逐渐减缓。 这主要是因为，随着楼板厚度从130 mm 增加到160 mm，其刚度的增加相对于质量的增加带给楼板的影响更为显著，刚度的增加消除了一部分质量给自振频率带来的不利影响，故自振频率随着楼板厚度的增加提升显著；而对于振动加速度而言， 楼板厚度的增加带来的影响在逐渐减弱。 实际工程中，应合理控制楼板的浇筑厚度在更经济的情况下满足振动舒适度要求。

4 结论

1） 通过对两块钢筋桁架混凝土楼板进行简谐激振试验，分析了楼板随不同频率、不同幅值的简谐力持续作用下的振动响应。 并使用ANSYS 建立了两块试件的有限元分析模型，计算的楼板基频和加速度峰值与试测值吻合度良好，由此验证了文中钢筋桁架混凝土楼板建模方法及简谐荷载下动力分析的可行性。

2） 同等条件下，钢筋桁架混凝土楼板的基频较开口型组合楼板更高； 在楼板中央施加人行激励时，130 mm 厚度的钢筋桁架混凝土楼板振动加速度峰值比同等厚度开口型组合楼板小65.65%，且两种楼板的加速度峰值均出现在第一步加载时刻。

3） 拆除钢筋桁架楼承板的底部钢板后，钢筋桁架混凝土楼板的基频降低了4.37%， 加速度峰值增加了19.76%。且模板厚度也一定程度上影响了楼板的振动舒适度。

4） 楼板厚度的增加对钢筋桁架混凝土楼板和开口型组合楼板的基频和加速度峰值均有显著影响， 两种楼板的自振频率随着楼板厚度的增加，接近于线性增长，而加速度峰值随着楼板厚度的增加变化趋势在逐渐减缓。