国际能源背景下中国能源市场风险溢出效应研究

韩光辉，张跃强，刘攀攀

(河北工程大学 管理工程与商学院，河北 邯郸 056038)

在区域经济一体化与多边贸易体系下，国际贸易相互影响程度加深，金融行业之间协同联动与风险传导更加明显，特别是原油、煤炭、天然气等能源经济，其价格波动会导致短期内国际能源行业发生巨大波动。原油作为一种大宗商品，其供需、库存、金融市场和地缘政治等因素都会影响油价。2020年5月美国WTI原油期货合约价格跌幅超过300%，最低跌至-37.63美元/桶，同期国内期货市场上，主力原油合约价格与上证能源指数分别下跌1%和1.7%。我国煤炭消费量全球占比最高，《中国能源报告2020》数据显示：2020年中国煤炭消费量超过40亿吨，占到能源消费总量的一半以上。中国煤炭交易市场作为新兴市场，其发展受到国际能源市场的影响。2021年随着世界经济正在复苏，国外煤炭价格飙升，中国煤炭价格涨幅也已超过60%。我国天然气期货发展较为缓慢，其受国际市场的影响较小。总的来讲，能源市场动荡的原因主要包括三个方面：供需关系、能源金融化、地缘政治。

一、问题的提出

如何有效测度现代金融市场在持续动荡背景下的风险水平和溢出效应，一直是监管机构与政府相关部门急需解决的问题。首先，在能源大宗商品价格剧烈变化下，许多学者对能源商品所存在的市场风险进行了分析。为提高定量模型在风险测度方面的稳健性和精确性，邹晓峰等[1]结合变点分析和极值指标对SV-T模型进行了改进。葛晓波等[2]将ARMA-EGARCH模型与极值理论相结合，对WTI原油期货风险进行度量，研究表明ARMA-EGARCH-POT模型能够有效描述原始数据的尾部分布并通过了后验测试。郑祖婷等[3]运用因子分析的方法确定碳交易价格风险的警兆指标，建立BP人工神经网络模型，对深圳市碳交易价格波动风险进行了有效的预测。Xu[4]采用时变GARCH-Copula模型和GAS模型分析了能源市场的最优风险对冲策略，实证研究表明，在衡量市场风险方面GAS模型优于GARCH族模型。

其次，当某一金融市场陷入困境时其他市场面临的风险，即风险溢出效应的研究，其主要研究方法包括CoVaR、VAR族模型和溢出网络方法等。国内外研究表明CoVaR方法具有优越性，并广泛用于测度金融市场中的溢出效应。CoVaR的概念由Adian和Brunnermeier(2008)在技术文件中提出，其计算方式有多种，主要集中为三种方法：第一种，分位数回归法。如欧阳资生等[5]采用分位数CoVaR法分析了我国44家上市金融机构的系统性风险溢出效应。严一锋[6]采用动态分位数法估计CoVaR，测度了我国银行业之间的风险溢出效应；第二种，Copula函数法。王皓晔等[7]将极值理论与Copula-CoVaR结合，针对“一带一路”倡议前后的国家股票市场之间的溢出效应进行了测度。李竹薇等[8]构建Copula-ARMA-GARCH-CoVaR模型对互联网金融与传统金融之间的风险溢出进行了实证研究；第三种，建立多元波动模型。陈挺等[9]通过建立DCC-GARCH-▽CoVaR模型测算出中美两国棉花期货市场间的风险溢出值，指出两市场之间时变的非线性相关性。戚逸康等[10]针对房地产板块不同时期对于股市的风险溢出效应，构建了BEKK-GARCH-CoVaR模型。

最后，国内学者对原油市场、煤炭市场等国际能源市场风险的相互影响进行了大量的研究。张大永等[11]采用网络联接的方法量化分析了我国原油期货与国际基准原油、上证指数以及人民币汇率之间的风险溢出与关联关系，研究表明中国原油期货市场处于信息的接受方，受到国际原油市场的正向冲击。刘映琳等[12]利用多重相关性断点模型研究了国际原油期货与我国商品期货市场中铜、橡胶和大豆的相关性，并使用VaR-EGARCH-SGED模型和VaR分位数回归模型，研究了国际原油市场对三类商品期货在高中低风险下的影响，指出我国商品期货与国际原油价格之间的相关性都呈现正向和周期性。Sun等[13]采用GARCH-Copula-CoVaR方法分析从石油和能源领域向海事转移的溢出风险，研究发现，大宗商品市场不仅对全球经济产生影响，同样对中国货运市场产生冲击。田园等[14]选取欧洲碳排放权交易系统中现货和期货数据，以及芝加哥气候环境交易所的数据，构造GARCH-EVT-VaR模型度量市场风险，并对比两个市场正常波动与极端情况下的市场风险，结果表明碳排放权交易市场下跌风险更大，并且负面信息对于市场的影响更显著。

综上所述，以往的研究偏向使用传统的波动模型度量市场风险，对GAS模型的应用较少，此外，针对风险溢出效应的研究主要包括原油市场与货币汇率或与其他现货市场，对我国能源行业的研究甚少。因此本文选取国际原油交易市场、煤炭交易市场、天然气交易市场以及中国上证能源行业指数数据，将基于得分函数的时变参数引入到广义自回归条件异方差模型(GARCH)中，选择拟合最优的残差分布，建立GAS-SKST滚动预测模型，并建立了传统指数广义自回归条件异方差模型(EGARCH)模型，进行回溯测试并比较了两种模型在风险度量中的信度。将GAS-SKST模型与分位数CoVaR结合，分析国际市场对中国市场的影响，最后针对中国能源市场的风险预警给出一些建议。

二、模型设定与变量操作

(一)GAS模型

广义自回归得分(Generalized Autoregressive Score，简称GAS)模型也称动态条件分数模型，由Creal，Koopman和Lucas(2013)提出，是一种以观测值驱动的时变波动参数模型[15]。GAS模型作为一种时变参数建模的框架，在预测模型中引入得分函数，通过参数变量导致变量和外生变量的动态来刻画时间序列过程的动态行为，为金融资产收益率波动建模提供了新的选择。

假设yt为金融时间序列观测值，σt为时变序列yt的标准差，表示时间序列数据的波动性，Ft-1为t-1时刻的信息集，则观测值yt概率密度函数为：

p(yt|σt,Ft-1)

(1)

GAS模型主要分为两部分，一部分是一阶自回归过程，另一部分则是数据驱动下的时变动态过程。GAS模型表达式为：

(2)

其中，当t=1时，σ1为无条件标准差，εt为标准化残差序列，Ai和Bi为时变系数矩阵，i=1,2,…,p，j=1,2,…,q，分别反映波动的时变性与波动的聚集性和均值恢复性，通常情况下p和q取1即可。ωt为常数向量，It为信息矩阵，St为放缩矩阵，一般情况下γ取0，此时St为单位放缩矩阵。▽t是与σt相对应的得分函数，其中时变参数σt到σt+1的更新过程采用的是牛顿-拉裴森(Newton-Raphson)法，是GAS波动模型的核心驱动项。

当标准化残差εt服从于不同的分布时，得分函数的表达式也会随之改变。针对金融时间序列，经常假设的分布分别为：高斯(正态)分布(N)、正偏态分布(SN)、标准学生t分布(ST)和偏斜学生t分布(SKST)，其中偏斜学生t分布的概率密度为：

FSKST(y;μ,σ,λ,ν)=

(3)

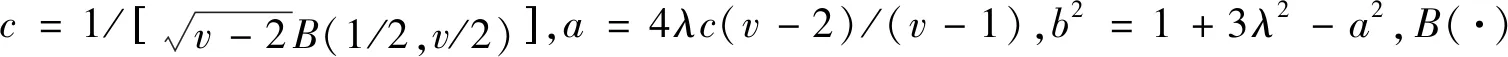
当标准化残差服从偏斜t分布时，其得分函数为：

(4)

由得分函数可知，偏度参数v与峰度参数λ决定了得分函数的取值。由于 GAS 模型是基于得分的，它利用了完整的密度结构，并且具有均值和高阶矩。随着v取值的增大，得分函数对极端值越敏感。偏度参数λ反映了得分函数对偏侧冲击的敏感性，当左偏分布时，得分对右侧冲击相对更敏感，当右偏分布时，得分对左侧冲击相对更敏感，当对称分布时，得分对两侧冲击的反应是对称的。

根据标准残差的条件分布，利用GAS的动态性，我们考虑以下参数动态更新机制：

(5)

(二)在险价值、期望损失和条件风险价值

在险价值(Value at Risk，简称VaR)。在险价值是投资银行JP摩根公司(1996)提出的一种量化评估风险的手段[16]。表示在一定置信水平q与持有期的条件下，投资者所拥有资产或者投资组合可能遭受的最大损失，其公式表达如下：

VaRq(X)=-inf{x|f(X≤x)>(1-q)}

(6)

其中q为置信水平，一般取0.99或0.95。x为收益率，f(x)为收益率的概率分布函数。VaR的本质是计算收益率随机分布的尾部分位数。

期望损失(Expected Shortfall，简称ES)。由于VaR无法捕获尾部风险，采用VaR确定监管资本要求时，不能准确地进行市场风险管理，低估了实际的市场风险，并且VaR不满足一致性风险测度性质中的次可加性。为了完善和提升市场风险度量方法，国外学者Artzner等(1999)提出了期望损失的概念[17]。ES的含义为当投资组合的损失超过VaR阈值时所遭受的平均损失程度。其公式表达如下：

ESq(X)=E[X|X≥VaRq(X)]

(7)

ES计算的是大于VaR的极端值的条件期望值，在VaR的基础上考虑了极端情况的均值水平。ES较之VaR更适合表达尾部风险，由于ES针对所有大于VaR的损失值进行度量，ES满足此可加性，是一致性风险度量。巴塞尔银行委员会于2016年重新搭建了Basel Ⅲ下的市场风险管理框架，提出了一系列新的计算标准，将市场风险内部模型计量测度从VaR转变ES，并规定这一转变于2019年起实施。

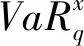
(8)

溢出风险贡献度。本文估计VaR所采用的为动态滚动估计，计算CoVaR的方式采取Adrian(2016)文章中的分位数回归法[19]，即：

(9)

则规定系统y对系统x的溢出风险价值为：

(10)

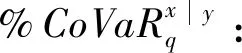
(11)

三、统计结果分析

(一)数据及描述性统计分析

为分析国际能源市场对中国能源市场的风险溢出效应，本文实证部分采用具有代表性的国内能源行业指数，即上证能源行业指数(SSEEN)。国际能源市场选取具有代表性的能源市场期货合约，分别为：WTI原油期货(USCL)、鹿特丹煤炭期货(AP12)、亨利港天然气期货(NGF2)，数据主要来源为英为财情。样本区间为2015年1月至2021年7月，剔除不匹配的交易日，选定样本容量一致为1600个。为方便处理，以收盘价对数的一阶差分作为对数收益率，即Rt=LnPt-LnPt-1，其中Pt表示第t日的收盘价，Pt-1表示第t-1日的收盘价。图1为价格历史趋势图与对数收益率序列图。

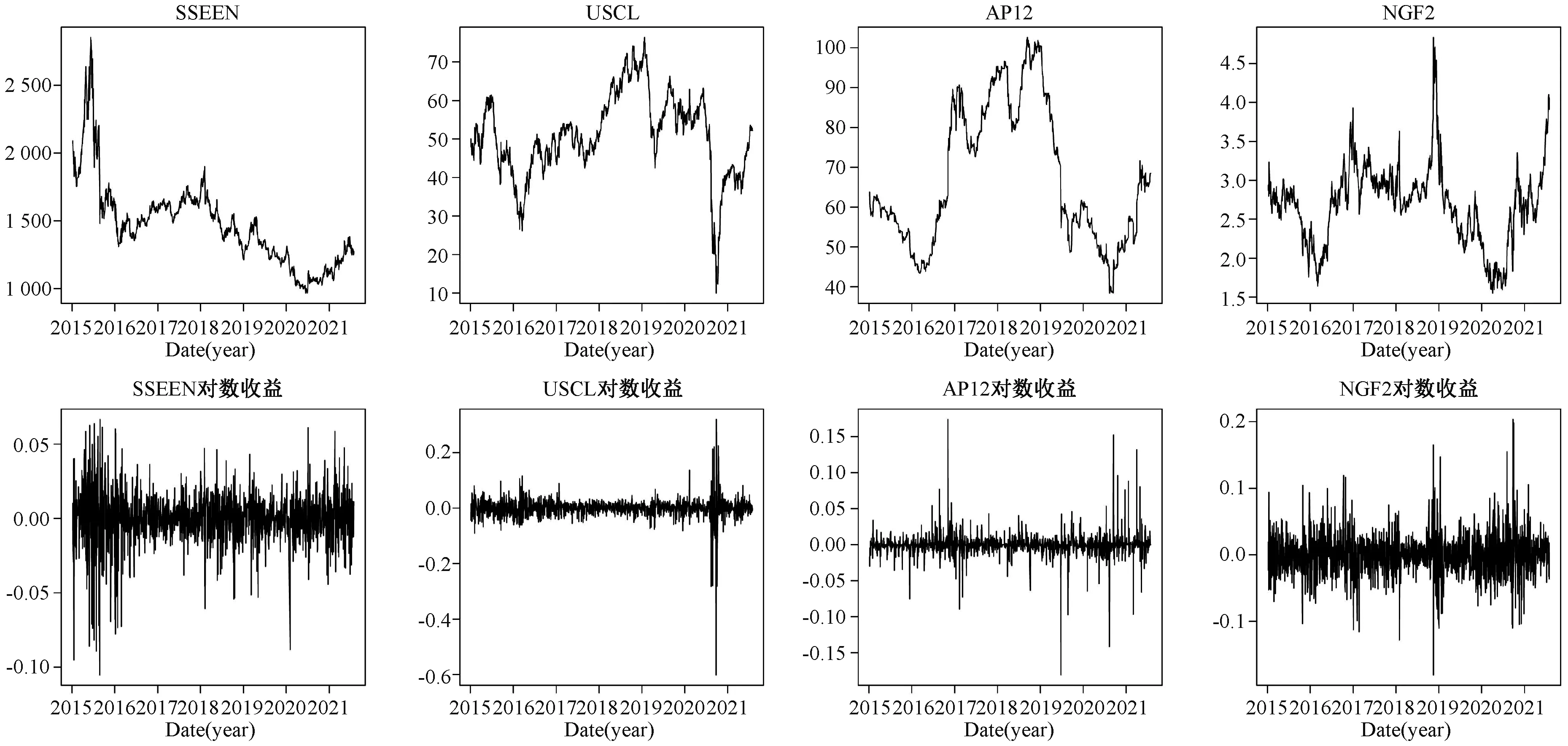
图1 价格历史趋势图与对数收益率序列图

根据价格历史趋势图，可以观察出国际能源市场上三种期货合约价格在走势上具有一定的同步性，特别地，在全球经济复苏形势下，国内能源行业指数及国际能源期货合约价格的走势几乎相同。从对数收益率图可以看出，能源市场普遍存在波动聚集性。对其对数收益序列进行描述性统计：

如表1所示，从日对数收益率描述来看，SSEEN、USCL、AP12和NGF2对数收益率均值都在0附近。从标准差可以推断，USCL的收益率波动最大，NGF2的收益率波动最小，其中USCL对数收益率上下幅度最大为0.92131。超值峰度系数均大于0，所有对数收益率序列具有尖峰性，其中USCL和AP12尖峰情况较突出。其中SSEEN与USCL偏度小于0，分布呈左偏，USCL和AP12偏度大于0，分布呈右偏。对该数据进行Jarque-Bera(1980)检验[20]，结果表明金融市场中收益率分布具有偏态并且尖峰的特征，并不服从正态分布，这与McNeil(1997)[21]对资产回报收益率的经验分布特征的研究结果相同。对日对数收益率进行平稳性检验，所使用的检验方法为ADF检验，因为显著性小于其显著性水平5%所以拒绝原假设 ,序列不存在单位根,是平稳序列。对原始序列进行自相关与ARCH效应检验，未通过检验，证明对数收益率之间存在自相关，残差之间存在自相关。

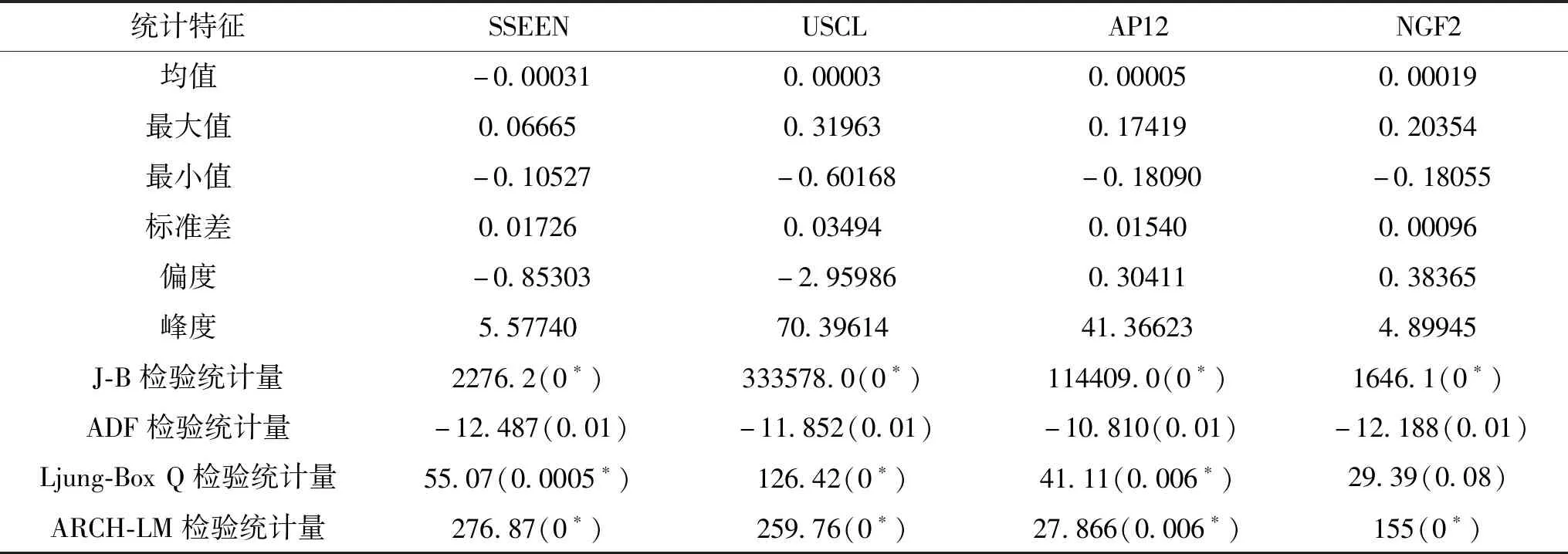
表1 对数收益率统计描述

(二)风险模型估计

因为GAS模型包括一阶自回归过程，能有效消除原始序列的自相关性，所以本文直接选择GAS(1,1)模型对各组收益率序列数据建立风险度量模型。模型参数的估计采用的方法为最大似然估计(MLE)，根据AIC准则和BIC准则，对比各种假设分布下模型的拟合效果。模型的AIC、BIC和对数似然值估计结果如表2：

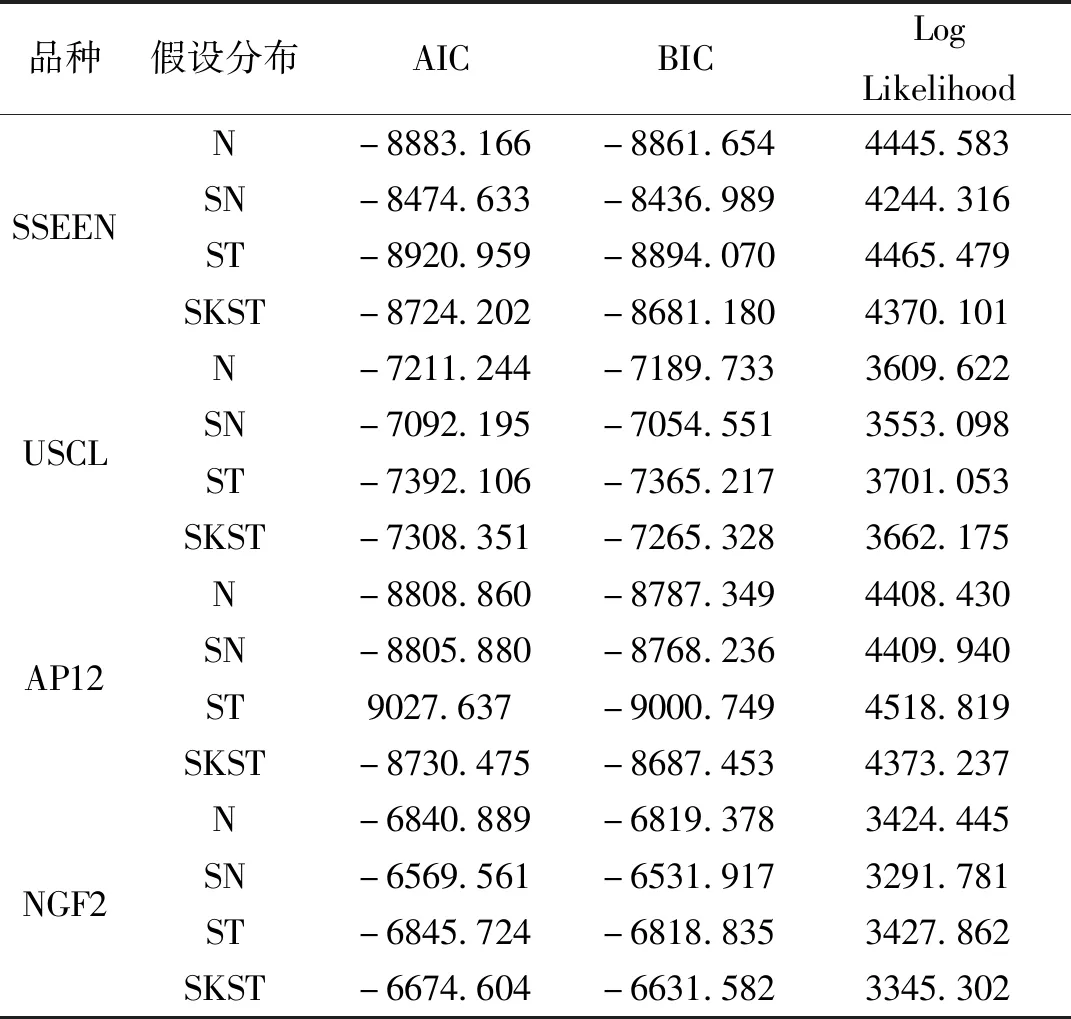
表2 GAS(1,1)模型AIC和SC估计结果

由表3可知，具有厚尾和尖峰特征的假设分布要明显优于传统假设的正态分布，其中拟合效果最好的为标准学生t分布，因为SKST分布变形包括标准学生t分布，所以选择假设分布为SKST。其参数估计结果如下：

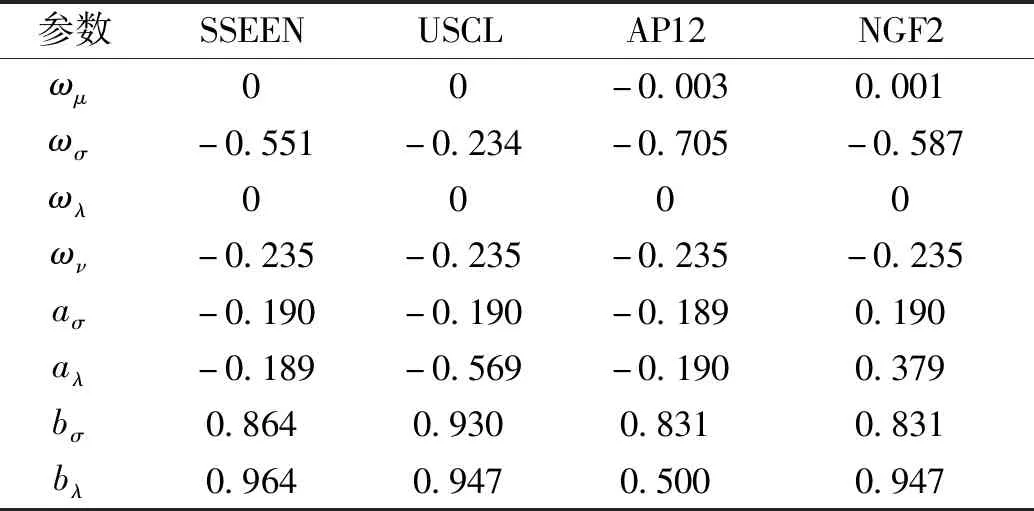
表3 GAS(1,1)-SKST模型参数估计结果

为展示GAS模型的时变性，将时变波动即条件驱动下的波动参数通过图像展示：

由时变条件波动图2可知SSEEN、AP12和NGF2在2015-2021年期间中间都存在断断续续的波动，AP12和NGF2时变条件波动趋势较为相似，说明两者存在较强的波动相关。USCL价格在2020年暴跌引起较强的一次波动，其他时间波动幅度较小，反观国际煤炭交易市场、天然气交易市场与中国能源市场，存在较强的波动聚集性，中国能源市场较之其他三者波动幅度较小。

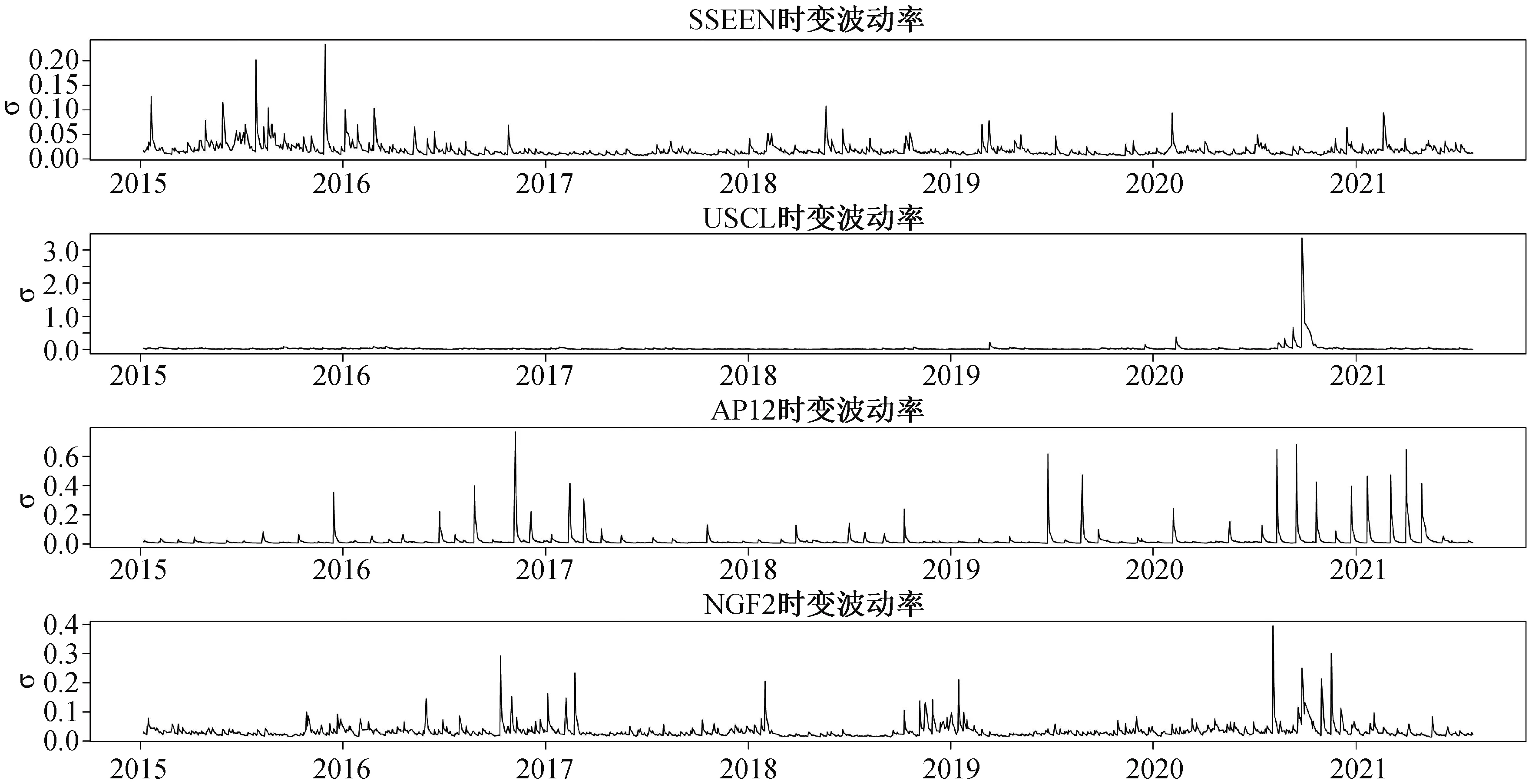
图2 时变条件波动图

(三)风险水平与溢出效应分析

1.我们利用GAS-SKST模型选择原始数据的前800天数据作为样本内数据，进行样本外预测。样本外预测数据为800天，滚动预测的固定窗宽为5天，每次向前一步重新对模型中的参数进行重新估计，参数不断更新，并计算q为0.95和0.99的VaR和ES。

预测结果如图3所示，以q=0.95为例，其动态VaR和ES描述统计如表4：

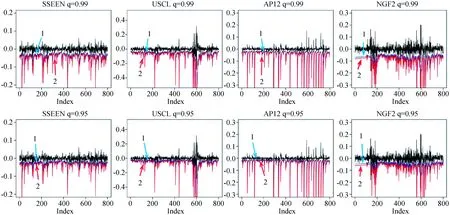
图3 滚动VaR和ES估计 注：图中1为VaR，2为ES

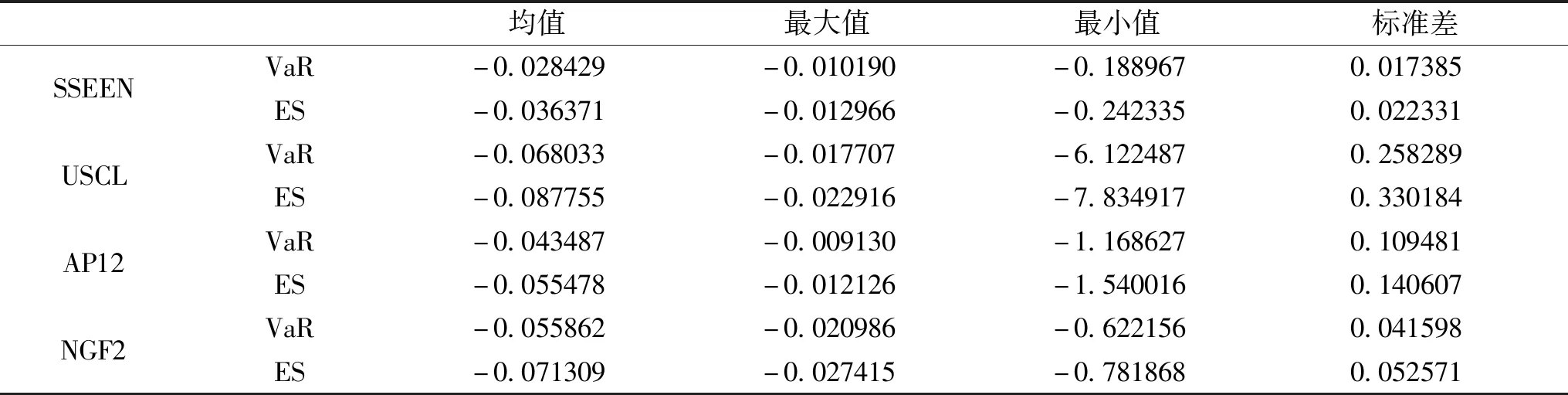
表4 动态VaR和ES描述统计

从动态VaR和ES描述统计看，根据VaR和ES均值大小可以看出，USCL风险最高，其次为NGF2、AP12和SSEEN。根据VaR和ES标准差大小可以看出，国际金融市场风险分布更加离散化，很明显国际金融市场下金融背景复杂，并且规模较大，当处于极端危险时，对于外界的抵抗较弱，易引起更大的损失。特别地，在风险管控、风险资本评估、投资组合收益风险评估及制定期货保证金应用上，ES较之VaR更具有优势。

为验证GAS模型的稳健性，建立同样具有一阶自回归的EGARCH(1991)模型[22]进行滚动预测并与之对比，设定残差分布为SKST，多项式中的滞后阶数为1。其表达式为：

(12)

对风险度量模型的检验采取Engle和Manganelli(2004)提出的动态分位数检验(Dynamic Quantile Test，简称DQ)[23]，此检验可以评估模型所计算的VaR的准确度，反映模型的稳健性，相比之下，DQ检验比LRuc和LRcc检验更有力。DQ检验本质上为解释变量矩阵W的线性回归模型，与W相独立的原假设定义为H0:Ht=I(yt<-VaRt)-θ。DQ检验统计量为：

(13)

其中，解释变量矩阵包括常数项、滞后项以及VaR序列,其他随着时间推移的相关的回归变量等，DQ统计量服从卡方分布。

通过DQ检验分别对两种模型下VaR值的有效性进行诊断，当q=0.95，即理论风险比率为5%，检验结果如下：

其中AD为观测值与分位数之间的最大绝对偏差。由表5可得95%置信水平下，USCL的AD值较大，证明原油期货存在较为极端的市场风险。EGARCH-SKST模型下USCL未通过检验，可知EGARCH模型并不倾向于度量存在极端情况下市场的风险，其他品种下模型表现稳健。采用GAS-SKST模型整体表现较好，DQ检验P值大于0.05，即通过检验，实际风险比率均处于5%附近，证明GAS模型在风险度量上的稳健性。

表5 DQ检验

为刻画SSEEN、USCL、AP12和NGF2收益率之间的相依关系，利用Kendall秩相关系数法来估计相互之间的相关系数。估计结果如表6：

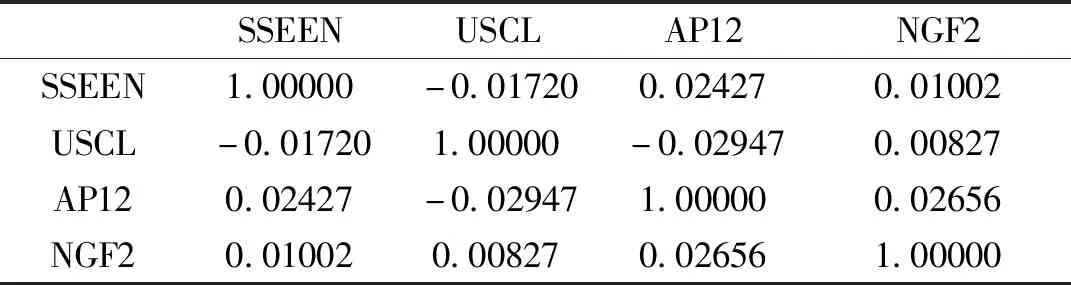
表6 Kendall秩相关系数

以SSEEN为例，由相关系数正负可以看出除了SSEEN与AP12，NGF2的收益率呈正相关，与USCL的收益率呈负相关性。从数值大小看，与SSEEN正向相依性最显著的为AP12。在经济全球化背景下，国际能源市场剧烈变动易对中国能源市场产生冲击。国际市场方面USCL、AP12和NGF2三个品种之间，USCL与AP12之间负相关性较强。

2.为度量国际市场下中国能源市场的风险溢出效应，并进行对比分析，利用分位数回归计算▽CoVaR与%CoVaR。当q=0.95时其描述统计如下：

表7 分位数▽CoVaR与%CoVaR

从表中数据看，国际原油市场对中国能源市场的▽CoVaR0.95为正值，证明原油市场对中国能源市场有双向的风险溢出，从%CoVaR0.95可以看出其风险溢出贡献度较小。中国作为全球最大的原油进口国，处于需求端，原油价格的波动增加了原油价格给中国经济带来的不确定性。但随着上海原油期货的上市交易，其功能逐渐完全，定价体系与风险控制能力逐步完善。值得注意的是，国际煤炭交易市场与天然气交易市场对中国能源市场的▽CoVaR0.95为负值，证明国际煤炭交易市场与天然气对中国能源市场有正向的风险溢出，其中煤炭交易市场风险溢出程度与贡献度较大。其主要原因可能是：煤炭仍是我国赖以生存的传统能源，煤炭生产量与消耗量居世界前列，其价格受国际市场与需求层面影响较大。而国际与国内天然气市场价格相对独立性较强，其风险溢出程度与贡献度较小。

四、研究结论与建议

研究表明：国际原油市场对中国能源市场有双向的风险溢出；国际煤炭市场与天然气市场对中国能源市场有正向的风险溢出；国际煤炭市场对中国能源市场的风险溢出贡献度远大于其他市场。此项研究有助于国内市场针对国际能源市场变动进行预警。

基于以上分析，能源始终是世界经济变化的主要风险源，提出以下建议：

(一)大数据技术及度量工具

现代金融经济信息公开化、透明化，金融行业更应注重利用大数据技术，使决策更加具有前瞻性。依托数据分析投资者的投资偏好，充分利用数据的信息价值，采用定性分析与定量分析下的多种工具，深度挖掘能源市场价格波动的影响因素，从而降低风险异常事件对自身潜在造成的威胁。以政府和银行为主导的监管部门应对数据进行挖掘和分析，建立数据平台，并将多种金融大数据分析的度量工具并用，深入研究风险源，对风险进行早期预警。

(二)实施动态风险监管

由于全球经济复苏，各国工业生产活动及社会经济活动往往需要能源支持，致使能源市场反复动荡。在经济的动态相关性下，风险冲击在每个阶段表现出不同的溢出效应与传染效应，所以要建立高效率能够迅速反应的监管平台，实时、动态地对风险进行监管。通过对能源市场信息以及其他市场信息、政策变动等异常事件的监测和实时分析，并进行反馈，达到对风险事件的实时监管，继而可以在风险可能爆发前及时预警，在风险产生后及时应对。

(三)增强能源市场协同性

在我国现有的能源期货中，原油期货在上海期货交易所挂牌交易，而煤炭期货在郑州商品交易所、大连商品交易所和上海煤炭交易所挂牌交易。相比之下煤炭交易平台较多，跨交易所的交易方式不利于煤炭交易信息的分享，对风险溢出监管和防控较为不利，易导致各交易所对于风险预警的滞后。宏观方面，不便于综合和统一监管整个能源期货市场，我国原油期货市场处于发展初阶段，需要政府、交易所、能源产业链等相关主体增强其针对市场反应的联动性，共同监督市场的运行状况。能源市场应针对行业间周期性风险进行调控，充分发挥了其价格发现和风险管控功能，进一步加强相关品种之间的协同性，从而规避风险。