考虑应变软化和冻融循环影响的粉质黏土修正双曲线模型

熊华涛

(中铁十六局集团铁运工程有限公司，河北高碑店 074000)

天然原状土多具有结构性，变形过程会伴随着土体结构的破坏，路基、地基等经过压实处理的重塑土则多处于超固结状态，由此土工构筑物中的土体往往会表现出剪胀、应变软化等特性[1-2]。在不同的土性、边界和周围环境等因素影响下，土体变形特性还会出现不同的变化趋势。其中，在寒冷地区，浅层地基和路基伴随季节变化出现的冻融循环过程会引起土体劣化，是影响工程稳定性的主要因素之一[3]。本构模型可以定量描述土体的变形和强度特性，因此建立考虑冻融循环影响的本构模型是寒区工程稳定性评价与预测的基本研究内容之一。

在考虑冻融循环影响的本构模型方面，文献[4-5]基于双曲线模型提出了新的归一化因子，包括极限偏应力和冻融循环损伤量，进而建立了冻融循环下粉砂土应力-应变关系的预测模型。崔宏环等基于岩土弹塑性力学体系下的屈服面理论，在p-q平面上以椭圆方程拟合体变屈服面，以抛物线方程拟合剪切屈服面，采用塑性关联流动法则，建立了考虑冻融循环影响的粉质黏土弹塑性本构模型[6]。常丹等指出可以分别采用椭圆型曲线和过原点的线性函数描述p-q平面上的体积屈服面和剪切屈服面；分别采用双曲线函数和对数函数表示剪切硬化参数和体积硬化参数与塑性应变的关系，其中函数系数均为以冻融循环次数为因子的三次多项式；进而引入非相关联的流动法则，建立了考虑冻融循环影响的双屈服面本构模型[7]。上述模型能够预测土体在不同围压和冻融循环次数下的应力-应变关系。问题在于，传统的非线性弹性模型和弹塑性模型均基于增量法概念，不能描述土体的应变软化特性[8]。上述考虑冻融循环影响的本构模型也是如此，仅能反映正常固结土的应变硬化特性。

为建立可以反映应变软化的本构模型，目前主要是在已有的非线性弹性模型和弹塑性模型基础上，采用不同的改进方法建立修正模型。Hashiguchi等提出了下加载屈服面的概念，为反映超固结土应力-应变关系提供了途径[9]。Asaoka等将下加载面概念与剑桥模型相结合，提出了上加载面概念，将其应用于超固结土和结构性土[10]。姚仰平等基于Hvorslev面、当前屈服面和参考屈服面之间的相互关系提出潜在强度概念，并将其与特征状态应力比引入到统一硬化参数中来建立超固结土的本构模型[11]。黄茂松等利用一个残余状态应力比和峰值应力比的公式来反映应变软化，建立了可以反映应变软化的双屈服面本构模型[12]。鉴于弹塑性模型表达式相对复杂，邓肯-张模型的应用仍然最为广泛和成熟，针对应变软化的修正方法也相对较多。Lee等指出邓肯-张模型的本质缺陷在于其反映的是线性的刚度软化，即割线弹性模量线性减小，但实际上土体刚度随应变增加而非线性软化，故不能反映应变软化及结构性的影响[13]。针对这一问题，沈珠江将损伤力学的概念引入土力学，提出损伤比的概念，建立考虑黏土结构破损过程的损伤力学模型，可以定量研究土的应变软化和逐渐破损现象[14-15]。王立忠等进而将应变软化型应力-应变关系分为三个阶段，在邓肯-张模型的基础上，引入损伤比的概念，建立了考虑土体结构损伤的修正模型[16]。Desai等将土体视为由处于相对完整状态和完全调整状态的两种基本部分所组成的混合物，基于扰动状态概念构造土的本构模型，为邓肯-张模型的应变软化修正提供了另一种思路[17]。王常明等基于扰动状态原理，以孔隙水压力为参量定义扰动函数，构建了描述结构性土不排水剪性状的邓肯-张模型，可以统一描述应变软化型和应变硬化型应力-应变关系[18]。此外，Fahey等基于割线模量定义提出一种新的双曲线模型形式，采用分段函数描述土体刚度的非线性软化规律，建立了可以反映应变软化的修正双曲线模型[19]。王军等采用基于割线模量定义的双曲线模型，预测了不同水泥掺入比黏土的应变软化特性[20]。综上所述，目前已有大量关于土体应变软化的本构模型研究，但是针对寒区岩土工程问题，尚未见到关于同时考虑应变软化和冻融循环影响的本构模型的研究报道。

针对上述问题，在大量冻融循环试验和三轴试验的基础上，分析了冻融循环影响下粉质黏土应变软化和刚度软化的变化规律，通过对Konder双曲线非线性弹性模型的拓展，基于双曲线函数形式和割线模量定义，变换得到割线模量与偏应力关系的分段函数表达式，即可以反映应变软化的修正双曲线模型。然后，拟合模型参数与冻融循环次数的回归关系，进而提出了能够反映应变软化特性和冻融循环影响的修正双曲线模型。

1 试验土样及方案

1.1 试验土样

试验土料为粉质黏土，颗粒级配关系为：小于0.005 mm的颗粒占15.2%，0.005～0.010 mm的颗粒占6.3%，0.01～0.05 mm的颗粒占37.9%，0.050～0.075 mm的颗粒占13.9%，0.075～0.250 mm的颗粒占11.6%，0.25～0.50 mm的颗粒占4.2%，0.5～1.0 mm的颗粒占5.5%，1.0～2.0 mm的颗粒占5.4%，其颗粒分布曲线如图1所示。土粒相对密度为2.64，液限为28%，塑性指数为10.3%，最大干密度为1.828 g/cm3，最优含水率为14.8%。以压实度100%和最优含水率为标准，采用分层击实法制取直径为39.1 mm、高度为80 mm的圆柱体试样。

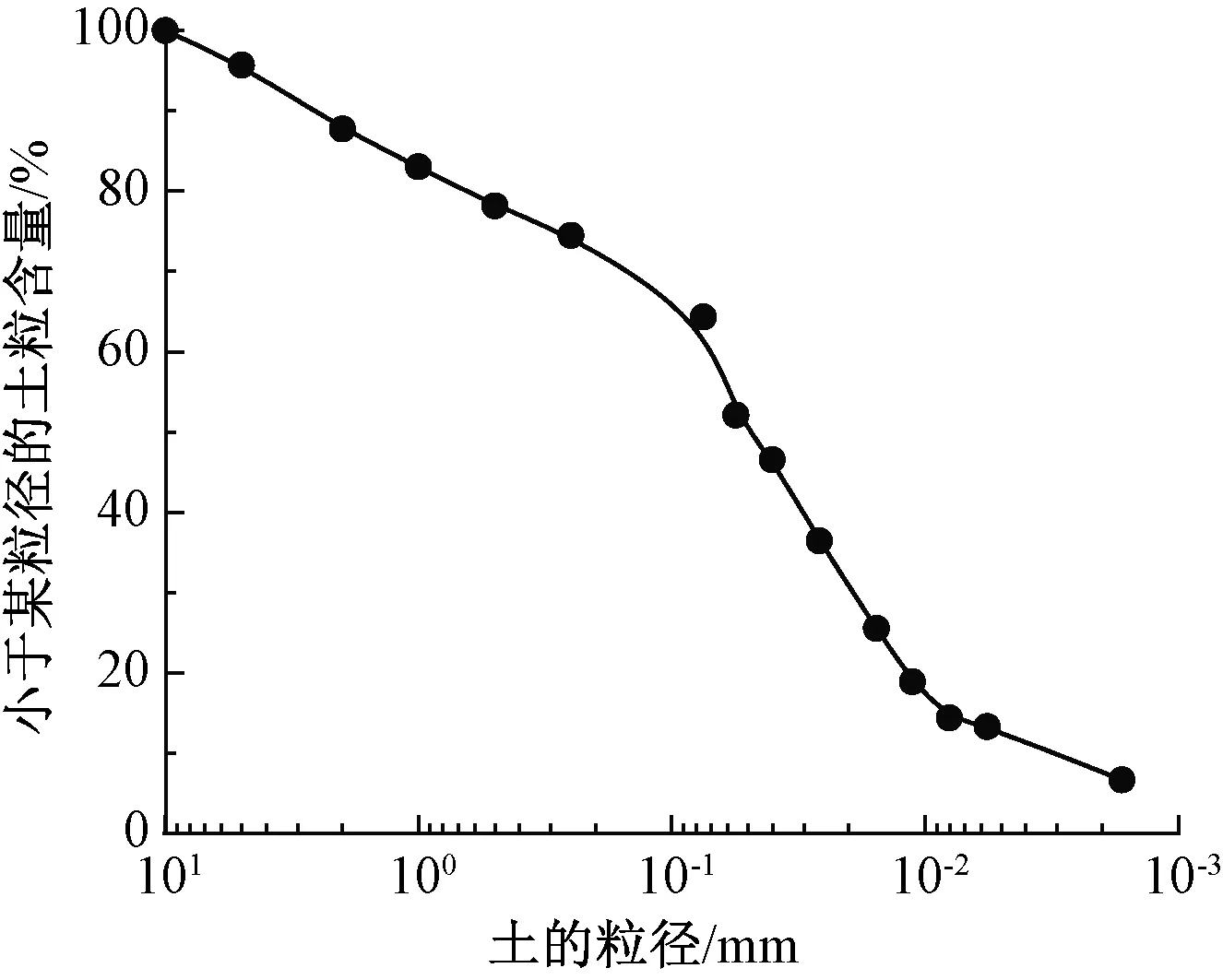
图1 土体颗粒分布曲线

1.2 试验方案

选择围压和冻融循环次数为试验变量，进行两个因素的全面试验。前期研究表明:1～5次冻融循环对土体强度的影响最为强烈，而后影响逐渐减小，趋于稳定[6]，因此取6次冻融循环为试验条件，研究冻融对土体强度的影响规律。围压分别选取20，40，60 kPa，冻融循环次数分别选取0、1、2、4、6次，共计15组试样。冻融循环试验在恒温恒湿试验箱中进行，环境温度分别设置为-5，20 ℃。冻结和融化时间各设置为12 h，以保证试样完全冻结和充分融化，此过程即为一次冻融循环。达到设计冻融循环次数后取出所需试样进行三轴试验，其余继续进行冻融循环试验。

由于低渗透性特征和压实过程的超固结应力历史，以及赋存环境和行车荷载特征，运营中黏性土路基的固结、蠕变通常仅在加载瞬间出现增大现象。因此，三轴试验类型为不固结不排水剪。试验仪器选用南京土壤仪器厂的TSZ-1型三轴仪，应变速率设置为0.5%/min，结束应变设置为20%。

2 试验结果及分析

2.1 应力-应变曲线

根据GB/T 50123—2019《土工试验方法标准》的要求，随着试样轴向应变的递增，对试样断面积和应力进行了修正。不同围压和冻融循环次数下试样的应力-应变关系试验结果如图2所示。可以看出：在三种围压下，应力-应变曲线均呈应变软化型，且随着轴向应变的增加表现为脆性破坏。应力-应变曲线位置随冻融循环次数的增加而逐渐下降，峰值偏应力对应的轴向应变呈现逐渐增大的趋势。峰值偏应力变化率随冻融循环次数呈逐渐增大的变化规律，减小率在20%以内，如图3所示。

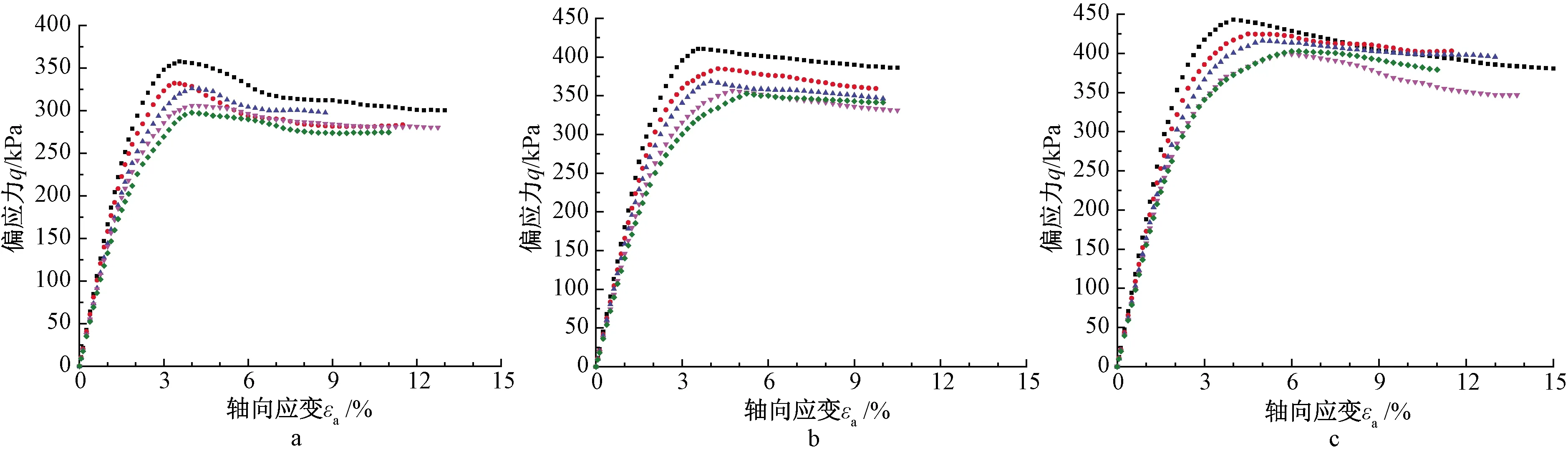
a—围压20 kPa；b—围压40 kPa；c—围压60 kPa。

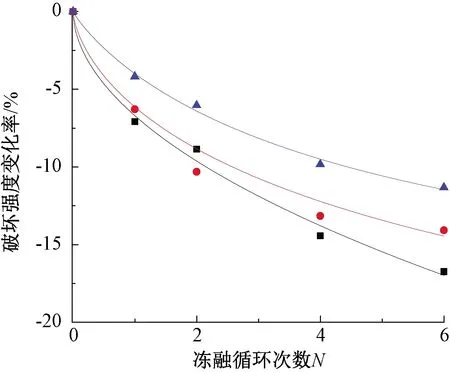
围压20 kPa；围压40 kPa；围压60 kPa。

2.2 刚度软化规律

静三轴试验中，常用割线模量Es的大小来描述土的刚度，割线模量的定义为偏应力-轴向应变曲线上某点与原点连线所得直线的斜率[1]，即式(1)：

(1)

式中：σ1、σ3为大、小主应力；εa为轴向应变。

图4为不同围压和冻融循环次数下试样的刚度-应变关系曲线。可以看出，割线模量随着轴向应变的增加而逐渐减小，即发生刚度软化现象。加载初期割线模量的减小幅度相对较大，之后随着轴向应变的增加而逐渐平缓。同时，随着围压的减小或者冻融循环次数的增加，相同轴向应变对应的土体刚度呈逐渐减小的变化趋势。

a—围压20 kPa；b—围压40 kPa；c—围压60 kPa。

3 修正的双曲线模型

3.1 基于割线模量的双曲线模型

Kondner提出土体加荷时的应力-应变关系可以采用双曲线函数表示为：

(2)

式中：q为偏应力；a、b为试验参数。

由于dσ2=dσ3=0，割线模量Es定义为：

(3)

在应变很小即加载之初时，试样处于弹性变形阶段，εa=0，Es=Ei，则初始模量Ei为：

(4)

当应变趋于无穷大时，理想双曲线关系渐进线所对应的是极限偏应力(σ1-σ3)ult，即：

(5)

极限偏应力在试验中不易测取，而土体的破坏强度可以确定。如果按照邓肯-张模型的方法，定义经验破坏比Rf为：

(6)

那么，双曲线模型可以表示为：

(7)

对于三轴试验，根据割线模量Es的定义对双曲线形式进行变换，则式(5)可以表示为：

(8)

式中：Es/Ei表示无量纲化割线模量；q/qmax表示无量纲化偏应力。

由式(8)可以看出，此时双曲线模型反映的q/qmax-Es/Ei关系为线性关系。根据冻融循环0次时的试验结果绘制q/qmax-Es/Ei关系曲线，如图5所示。图中直线即为邓肯-张模型假设的E/Ei-q/qmax关系特征。可以看出，随着围压的增加，q/qmax-Es/Ei曲线逐渐向直线接近。但是，q/qmax-Es/Ei实际上并不是线性关系，q/qmax达到1之前，Es/Ei随q/qmax的增加而减小，曲线向右发展；q/qmax达到1之后，Es/Ei和q/qmax同时减小，曲线转而向左发展，即开始发生应变软化。因此，q/qmax-Es/Ei关系是由两段曲线前后衔接而成的组合关系，应该采用分段函数对q/qmax-Es/Ei关系进行描述。

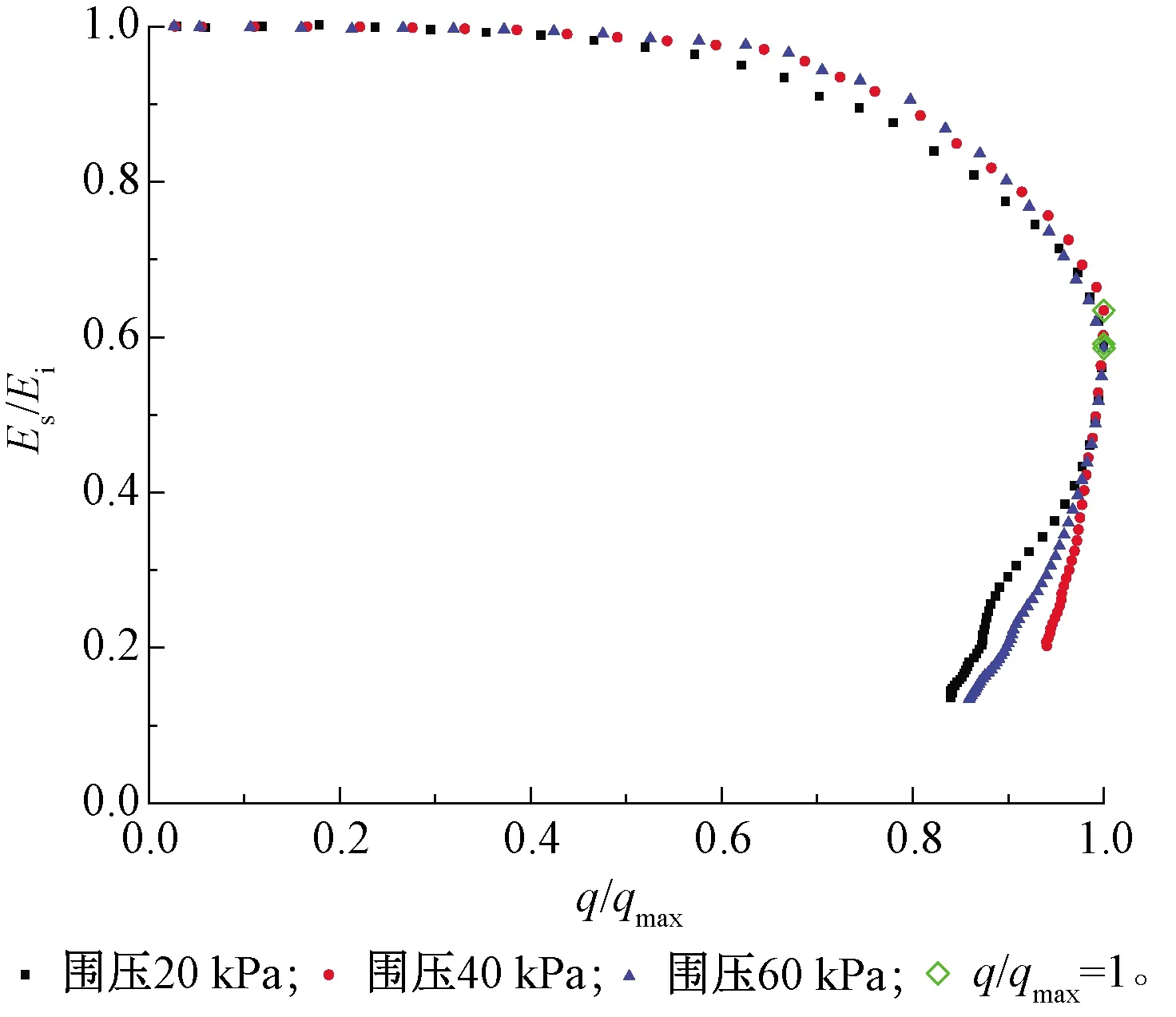
图5 冻融循环0次时试样的q/qmax-Es/Ei关系曲线

Fahey等分别采用幂函数和线性函数拟合试样应变软化前、后的q/qmax-Es/Ei关系[19]。由图5可见，试样应变软化前、后的q/qmax-Es/Ei关系中均呈非线性，因此均采用幂函数进行拟合，拟合函数形式如式(9)所示。

(9)

式中：f定义为破坏刚度比,近似等于Rf；g、β为决定曲线形状，其大小与围压和冻融循环次数有关，g=1时退化为邓肯-张模型形式。

式(9)即为可以考虑应变软化的修正双曲线模型，其中，对于初始切线模量Ei，其与围压有关，Janbu建议的经验关系为：

(10)

式中：K为材料参数；pa为标准状态下的大气压力，取值为101.3 kPa。

对于峰值偏应力qmax，根据摩尔-库仑极限平衡理论，qmax的计算式为：

(11)

式中：c、φ分别为黏聚力和内摩擦角。

因此，新的模型参数包括c、φ、K、n、f、g、α、β，共计8个参数，均可由常规三轴试验的应力-应变试验结果换算得到。

3.2 考虑冻融循环影响的修正模型

土体性质在冻融循环作用下发生劣化，模型参数会随之改变，因此通过确定模型参数随冻融循环次数的变化规律及相应的回归关系来反映冻融循环的影响。根据不同试验条件下的应力-应变关系试验结果，确定上述模型参数随冻融循环次数的变化规律及其函数表达式，包括c(N)、φ(N)、K(N)、n(N)、f(N)、g(N)、α(N)、β(N)。

3.2.1c(N)和φ(N)的确定

按照应力路径法，以(σ1+σ3)/2为横坐标、(σ1-σ3)/2为纵坐标绘制摩尔应力圆，作通过各圆顶点的平均直线，然后根据直线倾角及其在纵坐标轴上的截距计算内摩擦角和黏聚力，即：

φ=arcsin tanα

(12)

c=d/cosφ

(13)

式中：α为平均直线的倾角；d为平均直线在纵坐标轴的截距。

不同冻融循环次数下试样的不排水抗剪强度指标值如表1所示。可以看出，黏聚力随冻融循环次数的增加呈逐渐减小的变化规律，而内摩擦角呈逐渐增大的规律。两者与冻融循环次数的回归关系均可以采用Logistic函数进行拟合，即式(14)，结果如图6所示，拟合参数取值如表2所示。

表2 抗剪强度指标与冻融循环次数关系曲线的参数拟合值

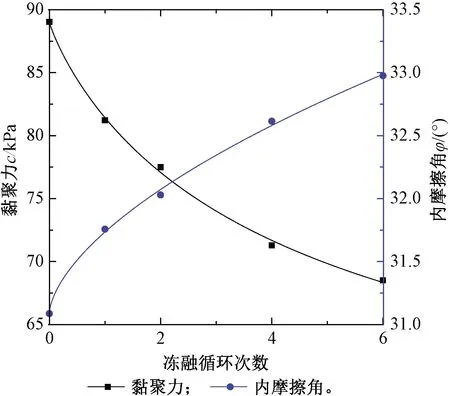
图6 抗剪强度指标随冻融循环次数的变化规律

表1 不同冻融循环次数下试样的抗剪强度指标值

(14)

式中：x0为未冻融试样的抗剪强度指标取值；N为冻融循环次数，A1、A2、A3为拟合参数。

3.2.2K(N)、n(N)的确定

根据不同试验条件下试样的初始切线模量Ei，绘制lg(σ3/pa)-lg(Ei/pa)关系曲线，如图7所示。可以看出，拟合直线的位置随冻融循环次数的增加而逐渐降低，直线斜率也随之发生改变。K和n的取值如表3所示，K随冻融循环次数的增加呈逐渐减小的变化规律，而n呈逐渐增大的规律。K和n与冻融循环次数的回归关系均可以采用Logistic函数描述，结果如图8所示，拟合参数取值如表4所示。

表4 K(N)和n(N)曲线的参数拟合值

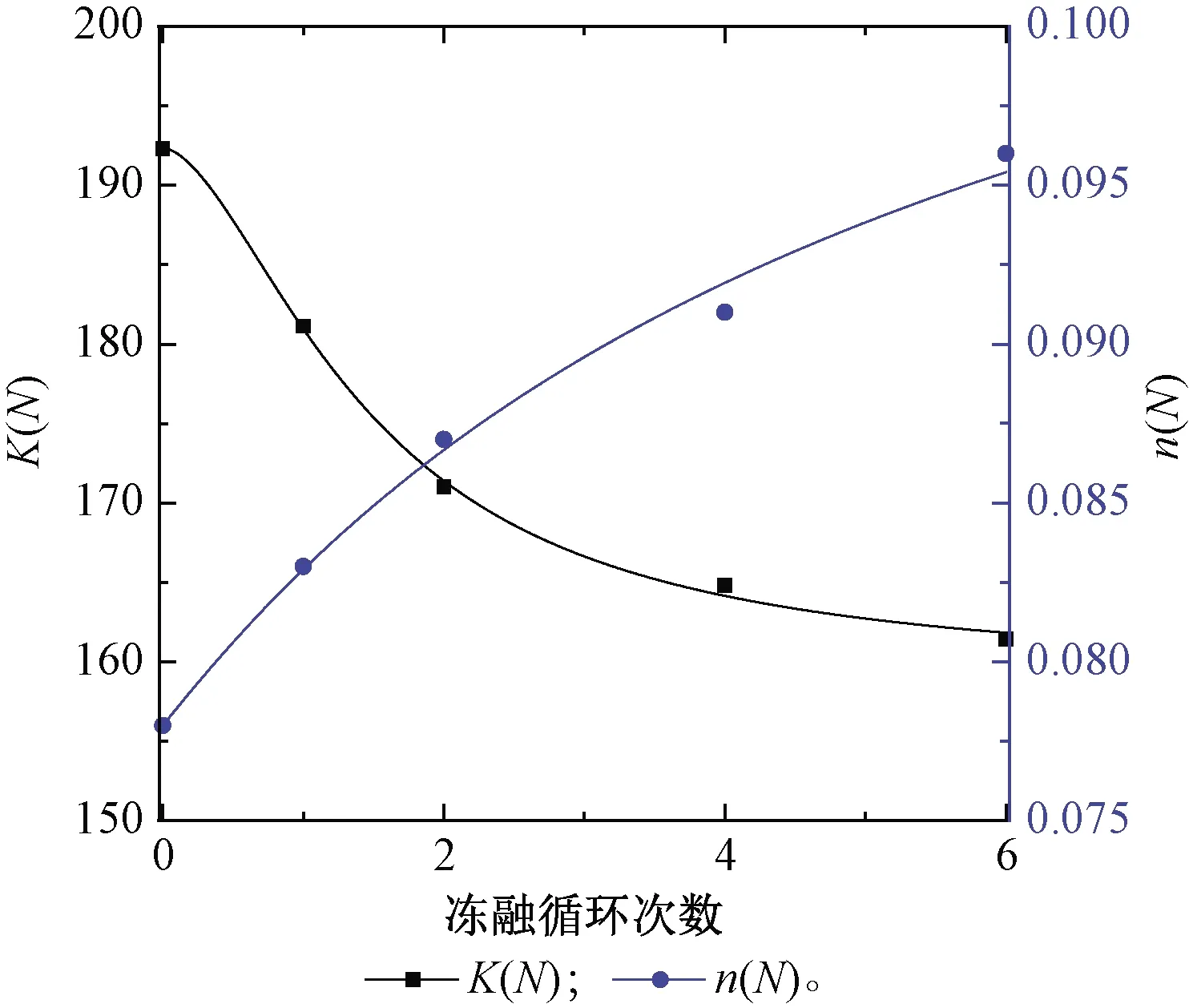
图8 K和n随冻融循环次数的变化规律

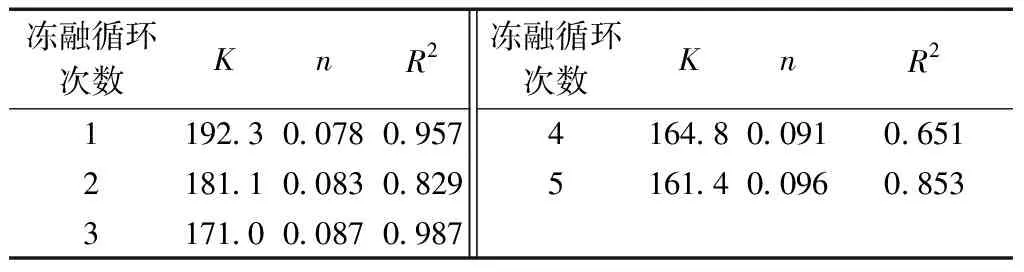
表3 冻融循环下试样的K、n值

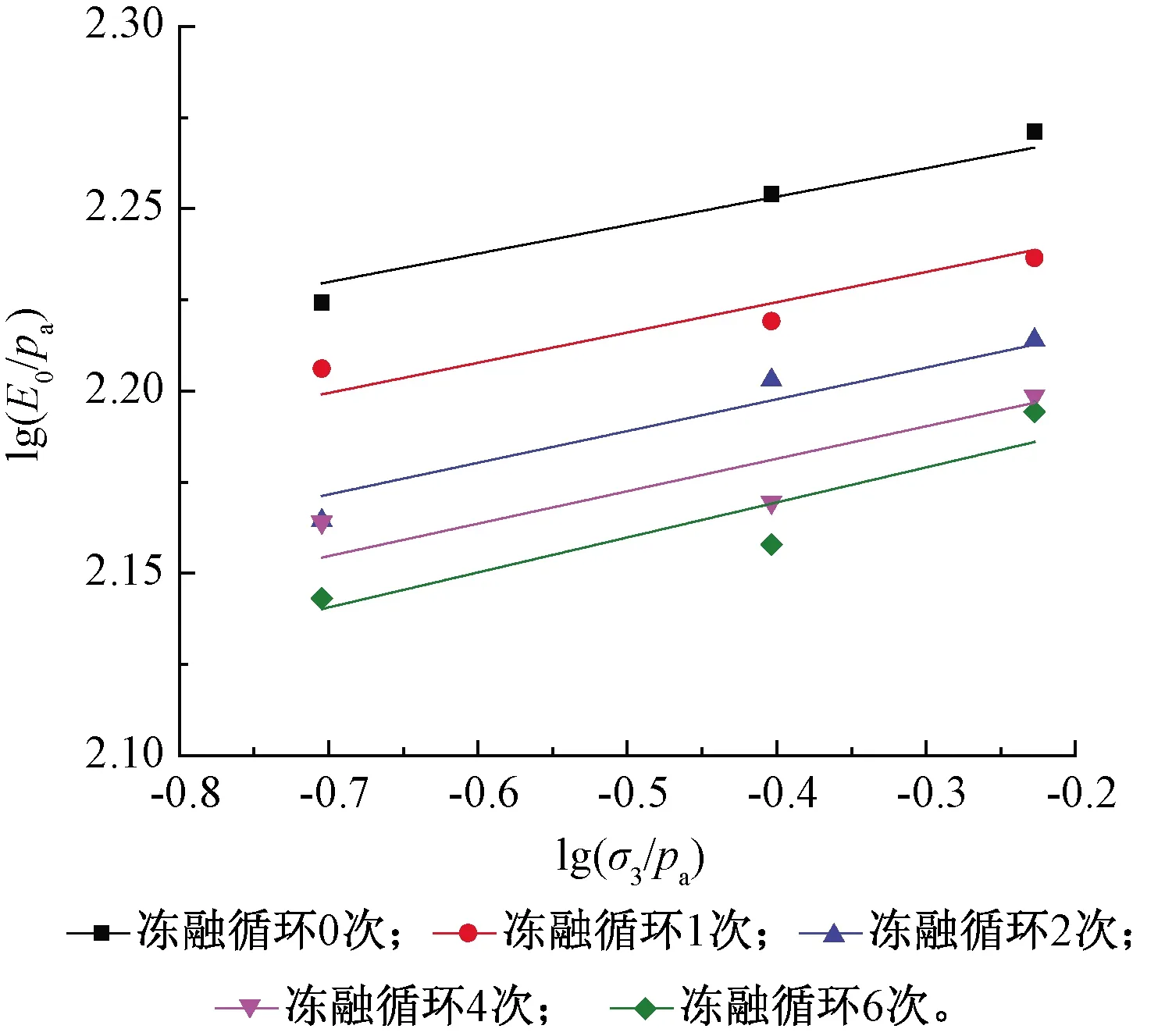
图7 冻融循环下试样的lg(σ3/pa)-lg(Ei/pa)关系曲线

3.2.3f(N)、g(N)、α(N)、β(N)的确定

根据图5无量纲化割线模量Es/Ei与无量纲化偏应力q/qmax的关系，然后通过式(9)拟合两者的回归曲线，结果如图9所示。可以看出：在应变硬化阶段，随着冻融循环次数的增加，相同围压下q/qmax对应的Es/Ei值呈逐渐减小的变化规律；在应变软化阶段，相同围压下q/qmax对应的Es/Ei值随冻融循环次数的变化规律则不明显，原因在于试样应变软化阶段的剪裂面发展具有一定随机性。

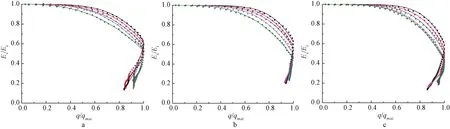
a—围压为20 kPa；b—围压为40 kPa；c—围压为60 kPa。

不同冻融循环次数下的f、g和α、β值分别如表5和表6所示。可以看出：随着冻融循环次数或围压的增加，f值呈逐渐增大的变化规律，g值呈逐渐减小的规律。f、g与冻融循环次数的回归关系均可以用Logistic函数拟合，结果如图10～12所示，相应的拟合参数取值如表7～9所示。不同试验条件下的β值则呈小幅度波动变化特征，说明试样应变软化阶段的软化趋势类似，因此β取平均值，结果为11.614。

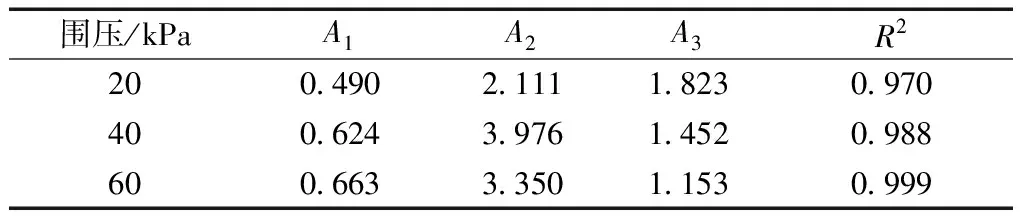
表7 f(N)曲线的参数拟合值

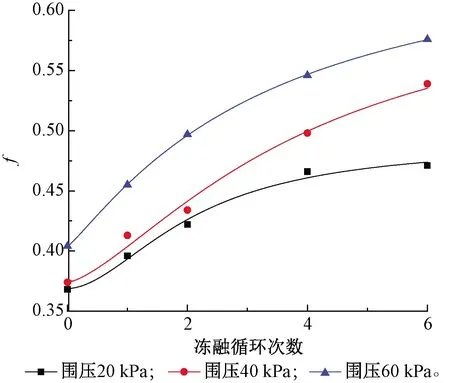
图10 f值随围压和冻融循环次数的变化规律

表5 不同围压和冻融循环次数下的f、g值

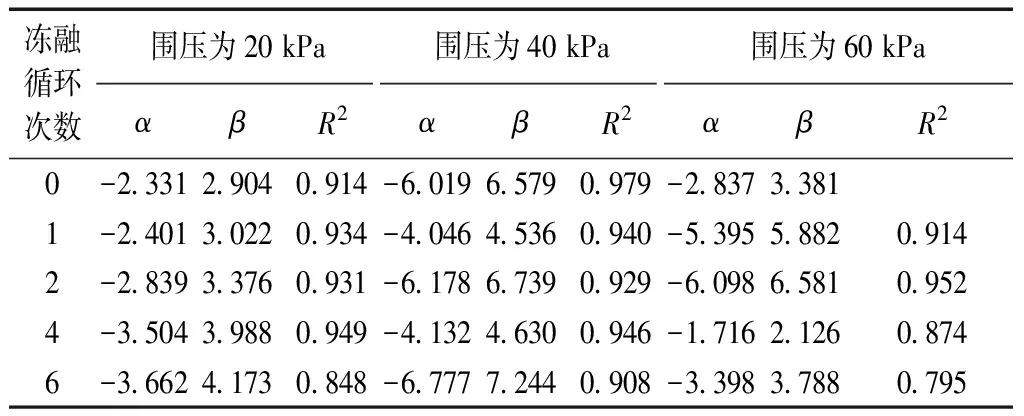
表6 不同围压和冻融循环次数下的α、β值

4 修正模型的验证

将上述模型参数的函数表达式代入式(7)，即得到以冻融循环次数为影响因子的修正双曲线模型。模型计算结果如图13所示。

表8 g(N)曲线的参数拟合值

由图13可以看出：在围压为20 kPa时，模型计算值与试验实测值吻合良好；在围压为50 kPa时，土体呈应变软化特征，未经冻融循环时峰值强度介于图1所示围压40～60 kPa，随着冻融循环次数的增大，峰值强度逐渐减小，且峰值强度对应的轴向应变值逐渐增大，与试验实测规律一致；模型可同时计算围压较大时土体的应变硬化特性。可见，该修正双曲线模型可以反映应变软化和冻融循环的影响。

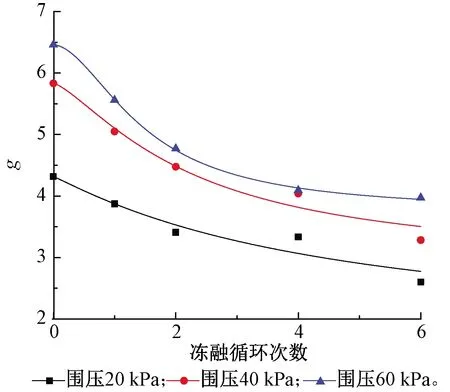
图11 g值随围压和冻融循环次数的变化规律

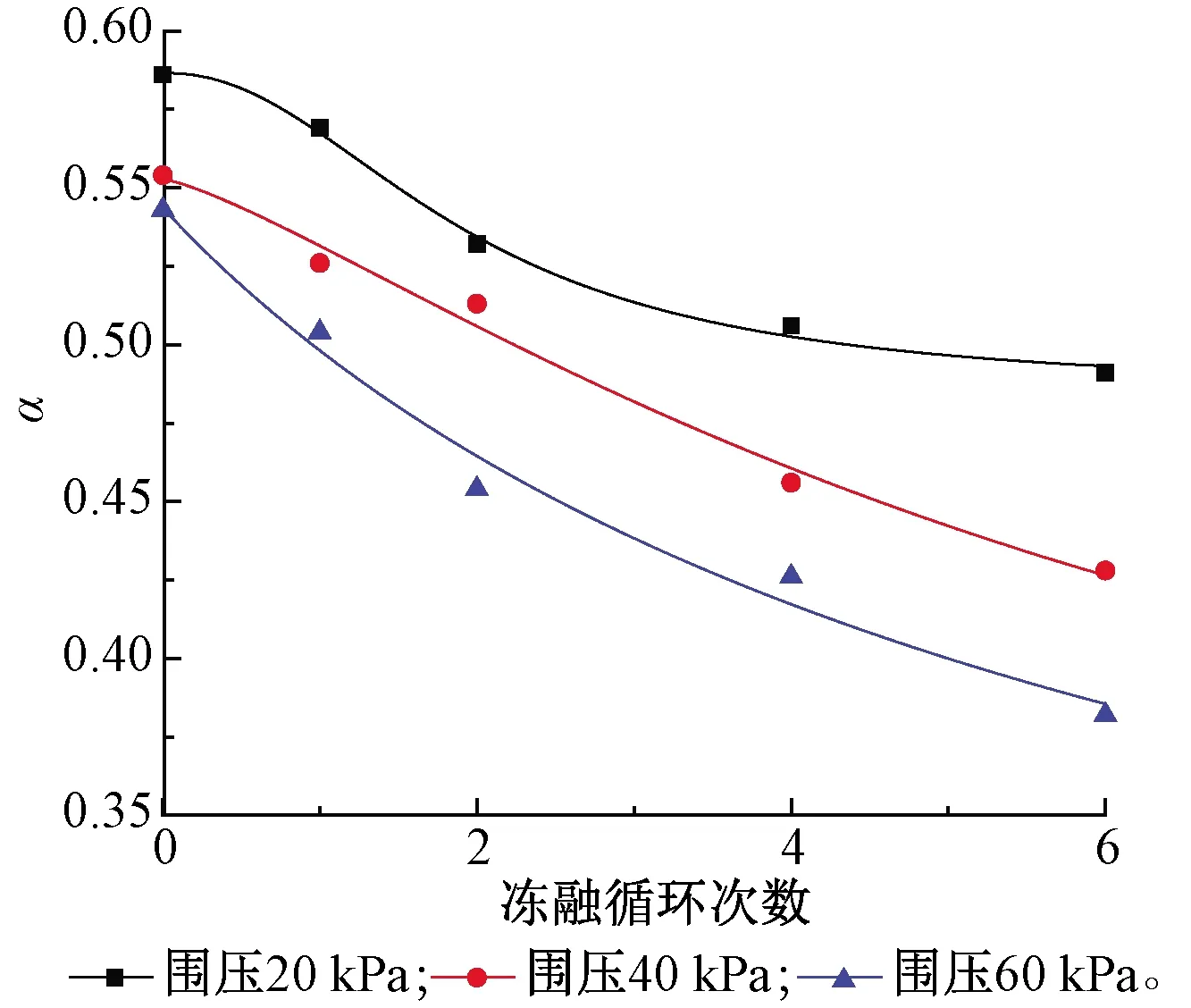
图12 α值随围压和冻融循环次数的变化规律

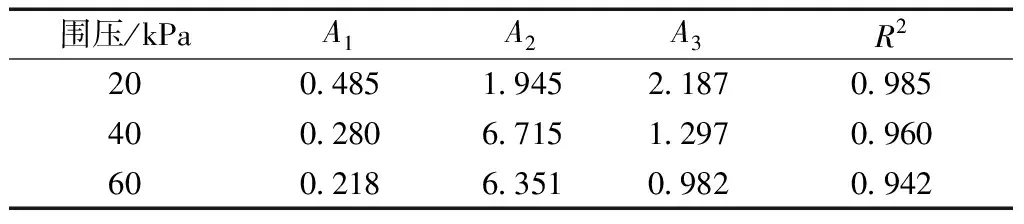
表9 α(N)曲线的参数拟合值

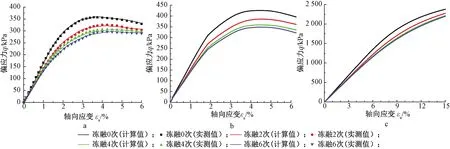
a—围压20 kPa；b—围压50 kPa；c—围压1 000 kPa。

5 结束语

1)按照割线模量定义对传统双曲线模型的函数形式进行变换，得到无量纲化割线模量Es/Ei和无量纲化偏应力q/qmax的关系函数。根据软化型应力-应变关系试验结果，分别采用幂函数和线性函数对应变软化前后割线模量随偏应力的变化规律进行描述，由此得到了可以反映应变软化特性的修正双曲线模型。模型包括c、φ、K、n、f、g、α、β共计8个参数，均可由三轴试验确定。

2)试样的峰值偏应力和刚度均会随围压的减小或冻融循环次数的增加而逐渐减小，可以通过确定模型参数随冻融循环次数变化规律，来反映冻融循环对应力-应变关系的影响。分析结果表明随着冻融循环次数的增加，峰值强度和黏聚力c逐渐减小，内摩擦角φ逐渐增大，初始割线模量E0逐渐减小，n值逐渐增大，f和α分别逐渐增大和减小，g逐渐减小，上述参数与冻融循环次数的回归关系均可以采用Logistic函数拟合。

3)将以冻融循环次数为因子的模型参数表达式嵌入Es/Ei-q/qmax关系函数中，即得可以同时考虑应变软化和冻融循环影响的修正双曲线模型。基于Excel电子表格编制修正双曲线模型的计算程序，结果表明模型可以计算土体的应变软化与应变硬化特性，计算值符合围压与冻融循环对土体的影响规律，表明基于割线模量定义的修正双曲线模型可以用来反映土体的应变软化特性和冻融循环效应。