基于TensorFlow的单层球面网壳结构极限承载力预测

兰 涛 丁 敏 底绍涵 郑飞鸿 庄金钊

(1.中国船舶重工集团国际工程有限公司，北京 100121；2.中国农业大学水利与土木工程学院，北京 100083)

人工神经网络(ANNs)是一种模仿动物神经网络行为特征来进行分布式并行信息处理的算法数学模型。这种网络依靠系统的复杂程度，通过调整内部大量节点之间相互连接的关系，从而达到处理信息的目的，并具有自学习和自适应的能力。神经网络具有非线性、非局限性、非常定性等特征，由于具有自我学习、联想储蓄、高速寻找优化解的能力在现代科学中发展迅速，在生物、数理、工程以及人工智能开发等方面有着非常广泛的应用。其中，以BP神经网络应用最为广泛，其发展对推动科学技术的进步具有重大意义[1-3]。

一直以来，由于非线性分析理论的复杂性、计算的困难性以及结果的不确定性对网壳结构的极限承载力的精确解带来了极大困难，阻碍了相关领域的研究。沈世钊院士在大量的非线性研究基础上提出了一种较为实用的回归公式用于网壳结构的稳定性分析，其结果与有限元分析所得出的精确解仍有所差异[4]。

在神经网络应用于网壳结构研究方面，吴剑国等最早利用BP神经网络对单层球面网壳结构的极限承载力进行预测研究，由于当时计算机计算能力的局限性，研究模型只包含了一个隐藏层，结果的准确度还有待进一步提高[5]；贺拥军等 针对网壳结构在强震下的失效模式进行分类和判别[6]，提出了基于神经网络强震失效模式分类判别方法；颜卫亨等为了分析轻型可移动折叠网壳结构的风压分布特性，提出了基于BP神经网络的风压分布特性预测研究模型[7]；徐菁等基于BP神经网络模型对网壳结构的损伤识别方法进行了研究，进一步讨论了影响损伤识别结果精度的因素[8]；崔胜红等针对网壳结构损伤识别中的模态信息不完备、模态局部化和跃迁现象以及结构自由度巨大等问题，提出了一种基于神经网络的结构损伤检测方法[9]；陈世英等利用BP神经网络对复杂非线性映射关系的模拟能力，针对网壳跨度、矢跨比与用钢量最少的网壳型式之间的映射关系，实现了网壳结构的选型优化[10]。

显然，目前利用BP神经网络对单层球面网壳结构极限承载力的研究较少，相关理论还处于初级阶段，本文将基于TensorFlow中的BP神经网络算法对这一领域进行探索，为后续相关研究提供方向和基础。

1 BP神经网络算法

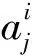
(1)

式中:wij表示神经元i与神经元j的连接权值。

第j个神经元的输出值为：

yj=∑fijai

(2)

式中：fij表示神经元i与神经元j的激励函数；ai表示最后一层隐藏层的第i个神经元。

BP神经网络的拓扑如图1所示。

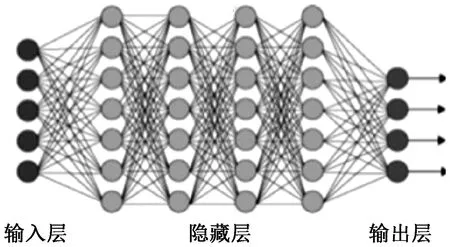
图1 BP神经网络拓扑

一般而言，在神经网络的学习阶段，给定模式{xi}作为网络的输入，要求网络通过调节所有连接权值和各神经元的阈值，使得在输出层神经元上得到需要的理想输出。实际上，我们希望找到一组确定的连接权值和阀值，以满足对所有输入下的输出预测，这不仅需要大量的数据，更需要一个合适的网络模型。通过图1可以看出，在BP神经网络中，输入层和输出层的节点数目都是固定的，模型计算结果的关键在于隐藏层数目的选择，隐藏层数目决定了神经网络工作的效果。

2 K8型单层球面网壳结构神经网络模型预测

单层球面网壳有肋环型、肋环斜杆型、三项型、Kiewitt型(简称K型)等各种形式，在这些形式中，以K型适用范围较宽，其网格比较均匀且易于划分，杆件种类相对较小，施工也比较简单，在工程中应用广泛。为使模型具有更好的适用性，选用应用最为广泛的K8型单层球面网壳结构作为本文分析对象，然后提出能够适用于Kn型网壳的神经网络模型。

2.1 样本数据

利用文献[4]已有数据，让BP神经网络对单层球面网壳结构的极限承载力进行学习，得出K8型单层球面网壳的极限承载力预测模型。

为考虑不同单层球面网壳结构的分割次数对神经网络预测值的影响，即网壳所包含的网格圈数的影响，在输入层中设置频数输入项，对模型进行训练。表1列出了部分学习样本(样本总数为64，样本数据取自文献[4])，其中：前7项是输入指标，分别为网壳的跨度、矢跨比、频数、主肋和环肋直径、主肋和环肋壁厚、斜杆直径和斜杆壁厚，第8项为考虑几何非线性有限元方法计算出的结构极限荷载。

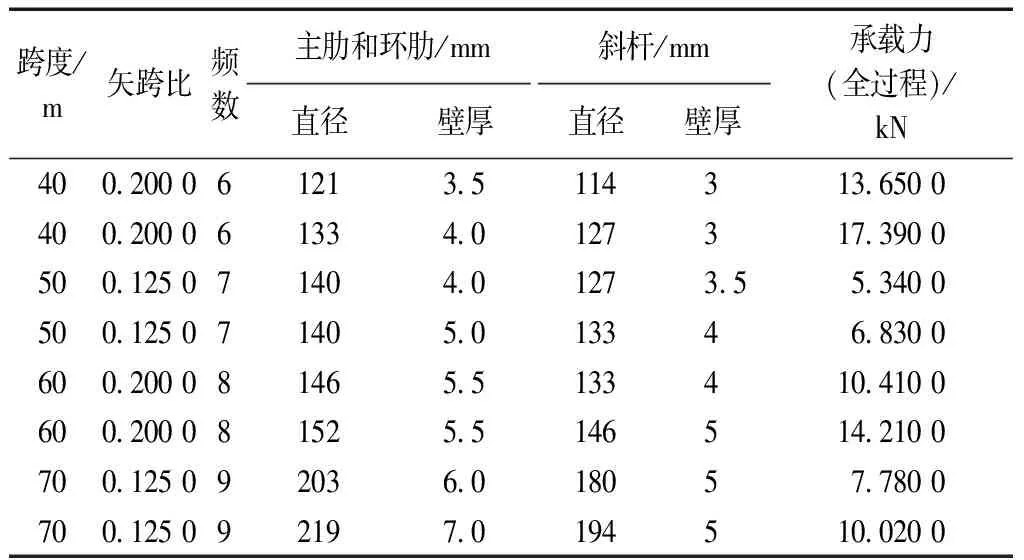
表1 考虑频数的K8网壳极限承载力部分训练数据

2.2 网络参数

采用BP神经网络对K8型单层球面网壳结构的极限承载力进行预测训练。表2分别列出了两种情况下的网络参数，第一行数据为不考虑频数影响的网络参数，第二行数据为考虑频数影响的网络参数。

表2 K8网壳网络参数

2.3 结果分析

采用有限元、不考虑频数影响的神经网络、考虑频数影响的神经网络和文献[4]中公式方法获得的K8单层球面网壳结构极限承载力部分结果如表3所示，相应误差分析结果如表4所示。其中Qcr(全过程)为通过有限元分析软件得出的单层球面网壳结构的极限承载力精确解，Qcr(回归公式)为采用文献[10]所推荐的回归公式计算得出的近似解。

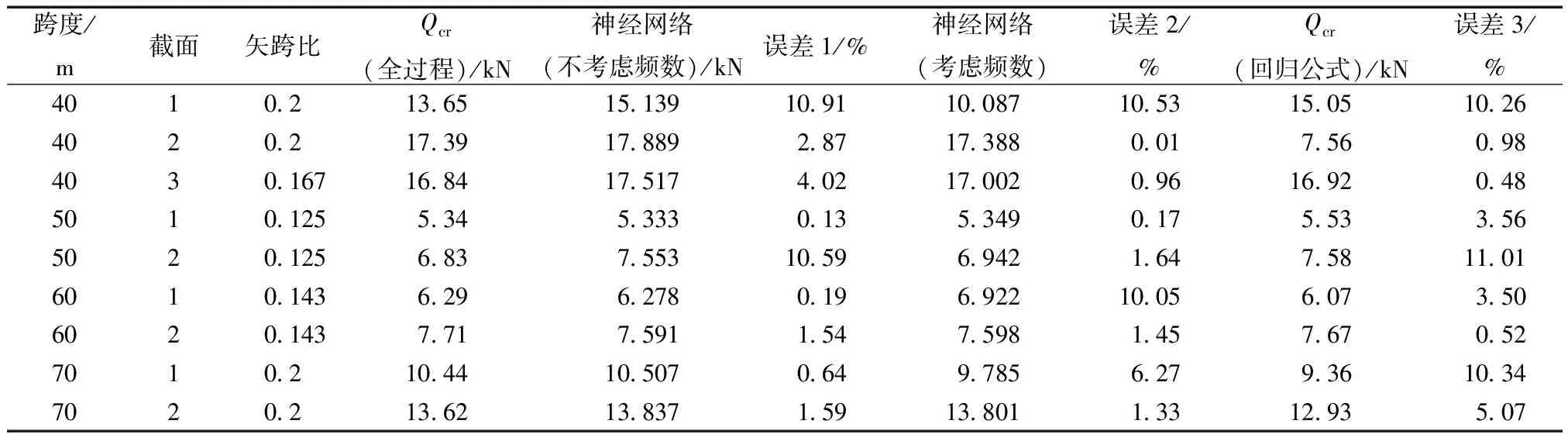
表3 K8型单层球面网壳结构极限承载力结果(部分)

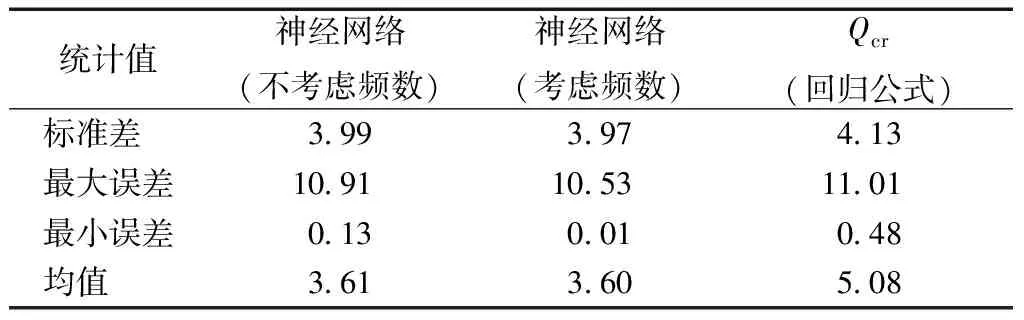
表4 误差分析

由表3和表4可知，不考虑频数的神经网络与考虑频数的神经网络大于10%的误差各有2组数据，回归公式大于10%误差的有3组数据；采用神经网络计算得到的结果的标准差与均值均小于文献[4]中回归公式结果，证明了采用神经网络预测K8型单层球面网壳结构的极限承载力的可行性。

3 Kn型单层球面网壳结构神经网络模型预测

3.1 样本数据

为了使模型具有更好的适用性，能够对不同的Kn网壳进行预测，在上一部分考虑频数的神经网络模型基础上，再增加一个Kn输入项。同时，为了测试模型的准确度，将96个样本分为84个学习样本和12个测试样本，即在网络中输入84个样本数据供神经网络系统学习，最后输入12个新样本数据对其进行测试。

3.2 网络参数

网络参数见表5。

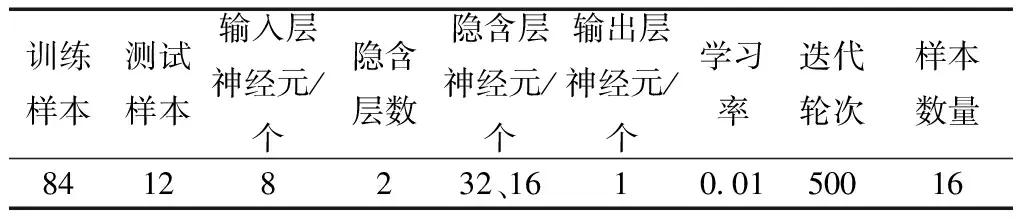
表5 Kn网壳网络参数

3.3 结果分析

采用有限元、考虑频数影响的神经网络和文献公式对12组新样本数据的Kn型单层球面网壳结构极限承载力结果如表6所示，相应误差分析结果如表7所示。

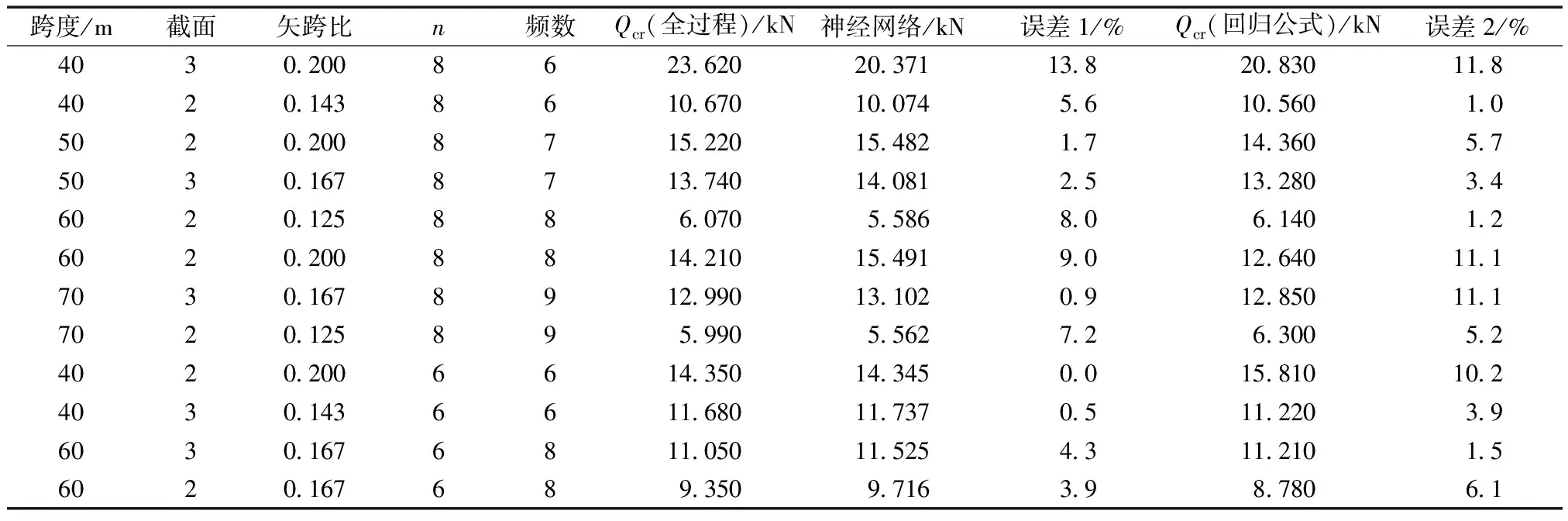
表6 Kn型单层球面网壳结构极限承载力结果

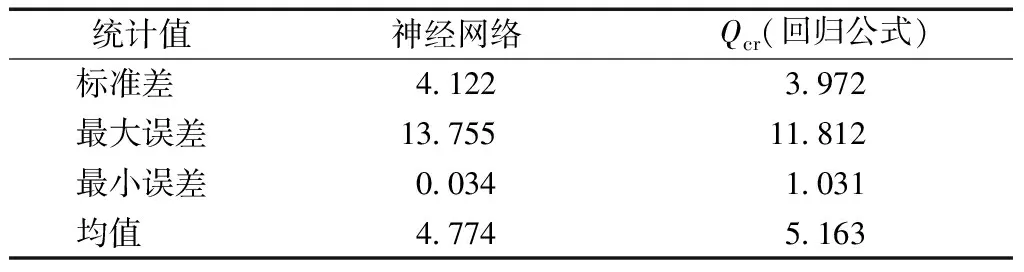
表7 误差分析

由表7可知，采用神经网络计算得到的结果的标准差为4.122%，与文献[10]所给出的回归公式的结果相差0.150%，证明采用神经网络预测任意Kn型单层球面网壳结构的极限承载力是可行的；最小误差0.034%与均值4.774%均小于文献回归公式，证明采用神经网络系统对任意K型单层球面网壳结构的极限承载力进行预测具有很大的研究空间。

4 结束语

1)通过BP神经网络对单层网壳结构的承载力极限预测时，考虑频数要较不考虑频数对结构承载力的影响较小，说明增加频数可以减小承载力计算误差损失。

2)在K8型网壳结构的模拟训练中，由于可供神经网络系统学习的样本数相对较多，K8型网壳结构的神经系统所计算得出的数据误差更小，说明样本数的增加会降低神经网络系统的误差。

3)在Kn型网壳结构的模拟训练中，神经网络系统的标准差与文献[10]回归公式相差不大，说明神经网络系统具有较好的学习能力和适用性。