基于混沌激光测距系统计算模型的深度图重建

蒋博文，岳涛，胡雪梅

（南京大学电子科学与工程学院，南京 210033）

0 引言

雷达是一种利用电磁波进行探测与测距的设备。随着科技的发展，除了传统的工作在无线电波段的雷达以外，还出现了工作在可见光和红外波段的雷达，这种雷达一般称为激光雷达（Light Detection and Ranging，LIDAR）。相比于传统的无线电雷达，激光雷达具有较高的精度与分辨率［1］，在机器人科学［2-3］、海洋探测［4］、大气探测［5］、智能驾驶［6］等领域有着十分重要的应用。

激光雷达以激光束作为信息载体，可以将电信号转换为光信号后发射出去，通过测量光信号在空间中的飞行时间即可计算出探测器到目标的距离。目前，采用非周期的随机信号进行测距成为了一种重要的遥感技术。NAGASAWA C 等［7］最早将随机信号应用于激光测距系统，但这种系统需要昂贵的随机码发生器，测距性能受限于随机码的码率。而混沌信号具有非周期定态、类随机性、宽频谱和自身相关性等特性［8-9］，可以通过确定性的非线性电路系统产生，因此用混沌信号作为激光测距系统的探测信号既可以避开随机信号发生器的性能限制，降低系统成本，又保证了探测信号的非周期性和随机性。最初，MYNENI K等［9］通过混沌激光脉冲序列实现了mm 级的高精度测距，他们通过比较回波信号和参考信号自相关函数峰值的时间差来确定信号的飞行时间；随后，LIN F Y 等［10］和王云才等［11］通过对回波信号和参考信号求互相关，并通过定位互相关曲线峰值在时间轴上的位置来确定飞行时间，实现了cm 级精度的探测和测距；除单目标测距外，王冰洁等［12］还实现了基于混沌激光雷达的多目标实时测距。

在混沌信号研究与激光测距系统仿真计算模型方面，LIN F Y 等［10］和王云才等［11］通过数值模拟得到混沌光信号，展示和分析了在不同参数条件下所产生混沌信号的功率谱、相位图、时域波形和自相关曲线，并分析了混沌状态和相关时间对混沌激光特性的影响，但他们的工作只对混沌信号本身的性质展开了研究，没有深入讨论将其应用于实际基于物理过程的测距任务和深度图重建时，各种退化因素对测距精度的影响；周国清等［13］基于MATLAB-Simulink 工具搭建了锯齿波、三角波和正弦波激光测距系统仿真平台，分析了不同调频连续波激光雷达的适用条件和范围，其仿真平台虽然是针对连续波激光测距系统而构建，但没有证明该仿真平台对基于混沌信号的测距系统同样适用；李海瑞［14］针对脉冲激光雷达系统成像的整个过程，构建了一款计算相对高效且可用于半实物仿真实验的仿真计算模型，确立了回波信号与激光发射器参数、接收器参数、大气传输参数和目标特性等之间的关系，但该工作仅对基于脉冲信号的激光测距系统展开了讨论，没有对基于包括混沌信号在内的连续波信号进行研究；朱娴［15］采用嵌入式计算机建模工具设计了一个激光雷达系统仿真软件，重点体现了软件的功能性和用户友好性，没有对基于实际物理过程的混沌激光测距系统展开深入定量的分析；崔洪鲁等［16］所提出的激光雷达回波信号仿真系统利用HITRAN 数据库重点研究了大气性质对光信号的影响，而没有考虑到完成一个实际的测距任务过程中其他环节的退化因素对光信号的影响。

虽然针对混沌激光测距系统的研究层出不穷，并且大量的仿真和实验结果已经表明，混沌信号在探测和测距任务中表现出了优越的性能，但目前有关混沌激光测距应用方面的研究主要集中在简单的目标探测和测距［7-9，12，17-19］与光纤故障定位［8，20-22］上，有关混沌激光在结合扫描系统的三维深度图重建上面的应用研究显得相对较少［14，23-25］。除此之外，尽管一些工作通过仿真模拟的方式分析了混沌信号的特性及其用于测距工作的可行性，或设计了一些针对传统激光雷达（调频雷达和脉冲雷达等）系统的仿真程序，但没有工作提出基于从混沌信号的产生到最后被接收和处理的整个实际物理过程的计算模型，也没有工作详细讨论和分析影响混沌激光测距系统准确性的主要因素，以及它在不同种类和不同程度的退化因素下所能表现出的鲁棒性。

基于上述问题，本文首先简要介绍了生成混沌信号的原理，随后提出了一个针对混沌激光测距系统完成一次完整测距过程的仿真计算模型。该计算模型从实际物理过程出发，相对全面地考虑到了从混沌信号的产生、发射、反射、接收，直至最后信号处理的整个过程中引起混沌信号退化并造成测距误差的各种因素，包括大气衰减、大气湍流、几何衰减、被测物体的表面法线信息及其双向反射分布函数（Bidirectional Reflectance Distribution Function，BRDF）、多径噪声、环境光噪声、系统热噪声和光电二极管的退化模型等，并通过MATLAB 软件实现了该计算模型的程序设计。最后，本文以通过三维建模软件合成的深度图作为待测场景，以一维蔡氏混沌信号作为探测信号，利用互相关法完成了在计算模型退化作用下的深度图重建仿真实验，并且着重讨论了BRDF、环境光噪声和多径噪声等退化因素对深度图重建质量的影响。

本文通过所设计并实现的混沌激光测距系统计算模型和在不同退化因素和退化程度下深度图重建的仿真实验，有利于为实现实际的混沌激光深度图重建系统以及针对影响重建质量的退化因素分析工作提供参考和依据，并有助于通过计算模型快速高效地构建大规模基于混沌激光测距系统探测的深度图数据集，为实现基于混沌激光测距系统的机器学习模型提供数据集基础。

1 基于物理过程的混沌激光测距系统计算模型

1.1 一维蔡氏混沌信号的产生

本文基于蔡氏混沌电路模型［26］仿真得到一维离散混沌序列，具体采用李亚等［27］提出的三阶多项式仿真得到用于混沌激光测距的混沌信号，其无量纲归一化状态方程为

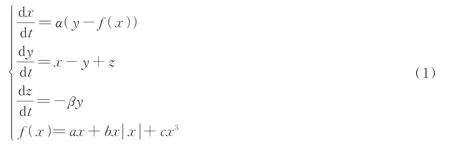
式中，α、β、a、b、c为决定所能生成混沌信号性质的参数。李亚等［27］取α=12，β=19，a=0.6，b=−1.1，c=0.45。本文参考了该组取值，但在此基础上进行了适当的微调，最终决定取α=10，β=16，a=0.5，b=−1.6，c=0.4，并通过实验验证得出该组参量取值能够生成符合测距要求的混沌信号。

本文基于MATLAB 软件仿真得到由式（1）所确定的三维蔡氏混沌吸引子，取其中的第一维并将其幅值归一化后，作为用于混沌激光测距计算模型实验的一维混沌序列。

1.2 混沌激光测距系统的测距原理与过程

产生所需的混沌电信号后，就需要将其输入到激光雷达系统，利用激光雷达的电光调制和光电转换功能完成测距。激光雷达一般主要由激励源、激光器、光束整形装置、激光发射机、激光接收机、光电转换器、回波检测处理电路、计算机控制与信号处理设备等模块组成［7］。由于本文所构建的混沌激光测距系统计算模型是针对实际的混沌激光测距系统而构建，因此为更好地描述计算模型，本文在详细介绍计算模型前，首先简要描述了实际的混沌激光测距系统的测距原理与过程，如图1所示。

如图1所示，在实际的混沌激光测距系统中，首先通过混沌电路产生混沌电信号，随后通过电光调制器将混沌电信号调制为混沌光信号，经过光束整形后，通过激光器将该混沌光信号向目标物体发射。混沌光信号经过在自由空间中的传播，到达目标物体后，一部分光信号会发生反射，并为激光接收机所接收。接着，通过光电转换器将激光接收机所接收到的光信号转换为电信号，最后经过回波检测后，通过计算机进行数字化的信号处理，具体来说是通过计算回波信号和参考信号之间的互相关曲线，来确定混沌光信号在发射和反射过程中的飞行时间，进而结合光速计算出光信号的飞行距离。本文将在第2.1 节更加详细地介绍基于互相关法的混沌信号测距原理。

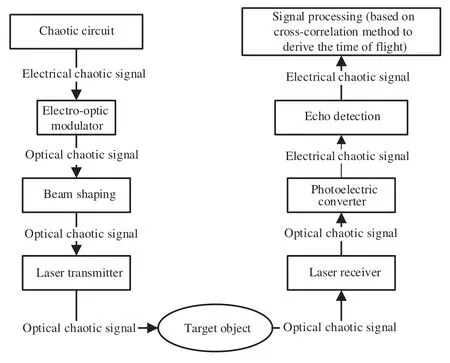
图1 混沌激光测距系统的系统结构和工作原理图Fig.1 The system structure and working principle diagram of the chaotic laser ranging system

本文主要围绕激光发射过程、被测物体的表面性质、激光反射及接收过程和光电转换器设计基于实际物理过程的混沌激光测距系统计算模型，同时假设激光器、光电转换器、发射端和接收端的功率放大器等器件均工作在线性区，不会引起信号的波形失真。

1.3 计算模型

1.3.1 大气衰减

1）大气吸收效应

文献［28］的仿真结果表明，大气对激光的吸收效应与激光传输距离之间的函数关系可以通过一条递减的洛伦兹曲线来描述。本文采用FANG Z B 等［29］介绍的洛伦兹函数形式

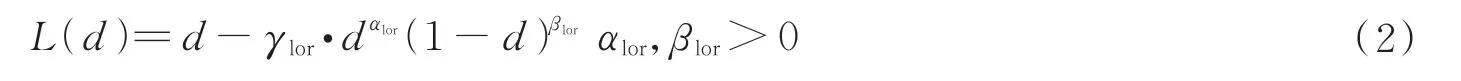
式中，L（d）表示激光传输距离为d（单位：km）时，由于大气吸收效应衰减后的能量与d=0 处能量的比值；αlor、βlor、γlor为决定洛伦兹曲线形态的特征参数，本文通过反复调整和试验，最终确定取αlor=1.02，βlor=0.92，γlor=0.96，获得了与文献［28］中基本一致的洛伦兹特征曲线。

2）大气散射效应

激光通信中的大气散射效应可分为瑞利散射和米氏散射两种［28］。瑞利散射效应对光信号所引起的衰减程度可以通过瑞利散射系数的微观表达式定量地描述为

式中，n为大气折射率；ρ（h）为海拔高度为h处的大气密度与海平面处大气密度的比率；Natmo=2.504×1025为常数，表示标准大气状态下每立方米的大气分子数；λ为入射光的波长，本文所采用的激光波长为λ=1.55 μm；Ray（λ，h）为所计算得到的瑞利散射系数，表示一定能量的光束与单个大气分子碰撞后发生散射而损失的能量分数。本文假设所仿真的混沌激光测距系统位于海平面高度，故此时在式（3）中，有n=1.000 29，ρ（h）=ρ（0）=1。

因此，若激光在海平面高度处的大气中传播一段距离后，与m个大气分子发生了碰撞，则其功率衰减为

式中，表示激光的传输距离为d时，由于大气分子的瑞利散射效应而衰减为的功率。

进一步假设大气条件在本文所仿真的测距空间范围内为标准状态（273.15 K，101.3 kPa），且保持恒定，则可以通过式（5）计算出激光在传播过程中与大气分子发生碰撞的次数m

式中，V表示激光光束在传播过程中所覆盖的空间体积；Phit表示光子与相应空间中的各个大气分子发生有效碰撞的平均概率。

本文通过下面的方法定量计算V的大小。由于光的衍射效应，即使激光器出射口的束腰半径很小，激光在从出射口发射出去后，也会以一定的发散角向四周发散开，导致光束半径随传播距离的增加而扩大。设激光发射时光束半径为r，出射后的半发散角为θ，则经过距离d后，光束半径将由于发散角的存在而扩大到R，此时激光光束在空间中的几何形状将呈一个圆台形，如图2所示。根据图2所示的几何关系，可以解得激光在传播距离d后的光束截面半径R为

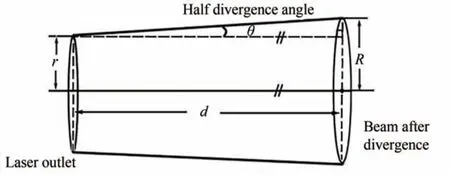
图2 激光发射并传播一段距离后其光束在空间中的几何形状Fig.2 The spatial geometry of a laser beam after it is emitted and propagated for a distance

再结合圆台的体积公式，解得光在传播过程中所覆盖的空间体积V为

米氏散射主要描述了大气中的气溶胶对激光的散射效应。气溶胶粒子的汇聚在宏观上形成了雾霾、雨雪等天气现象，并对于能形成雪花、雨滴或雾滴的这种尺寸较大的气溶胶而言，其对光信号的吸收作用可以忽略不计［30］，因此本文直接将各不理想天气状况下大气衰减的典型值近似作为米氏散射效应所引起的光信号能量衰减。

1.3.2 大气湍流

大气湍流会导致在近地大气环境中传输的激光产生光束漂移和光强起伏等效应［31］。接收端光斑漂移量与大气折射率结构常数C2n有关。在C2n∈[10-17，10-12]的区间内，光斑漂移量的均方根差值（Root Mean Square Error，RMSE）基本与C2n的三次方成正比［31］。因此根据三次函数的性质，在大气湍流较弱时，光斑漂移现象不明显，但随着C2n的进一步增大，光斑漂移现象的严重程度将迅速增加。本文假设回波光束在接收平面上所形成光斑的强度服从二维高斯分布，即光斑的几何中心强度最大，从中心出发沿半径向外强度按高斯函数衰减。因此，当发生光束漂移时，由于光束中光强最强的几何中心偏离了激光接收器，故将导致回波信号的信噪比降低。

光强起伏是指光信号的强度因受大气湍流的影响而发生波动，可等效为在光信号中引起了噪声。光强起伏方差同样是关于大气折射率结构常数C2n的函数，并且随C2n的增大与光斑漂移量均方差有相同的变化趋势［31］。因此，本文仍采用三次函数曲线对光强起伏方差随C2n的变化进行拟合。

另外，大气湍流效应还会导致激光光束偏离原来的发射和反射路径，造成所接收到的光信号不是由所期望的被照射点反射而来，即激光在空间中行进的距离将有所变化，最终导致测距误差和深度图重建质量的下降。但因为本文所采用的合成深度图空间分辨率较低，因此该现象所导致的重建误差在本文的实验设置下将不明显，只有当深度图的空间分辨率进一步提高时，该现象所造成的重建误差才会逐渐显现。

1.3.3 几何衰减

如1.3.1 小节中图2所示，随着传输距离的增加，激光光束将以一定的发散角向四周发散开来，引起光信号能量的分散，最终导致混沌激光测距系统中被测物体表面单位面积所接收到的光信号功率（即光功率密度）减弱，从而降低接收端的信噪比。

1.3.4 被测物体的表面性质

对于具有非漫反射表面性质的物体，其反射光的光场强度分布与物体的表面法线方向和光的入射方向具有很强的相关性，这种相关性可以通过BRDF 来描述。本文采用GGX 模型［32］构建被测物体的BRDF，其公式为

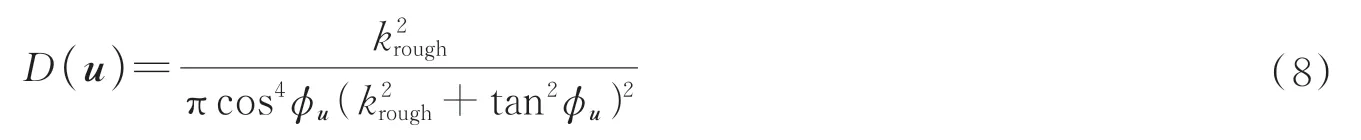
式中，u为入射向量；ϕu∈[0，π/2]为u与入射点处表面法向量的夹角；krough∈(0，1)为表征物体表面粗糙度的常数，与实际物体的表面材料特性有关；D（u）为给定入射向量u时，由于物体的表面反射性质而得到的归一化相对反射强度。

然而，GGX 模型对于具有较强漫反射性质的表面反射情况不能很好地表现，因此本文在式（8）的基础上增加了一项直流分量diff，用于表示物体表面反射光信号中的漫反射成分

式中，diff 为任意非负常数；D（u）为给定入射向量u以及如式（9）所示添加了diff 直流项后重新归一化的相对反射强度。

由式（9）可知，在GGX 模型下，物体表面的法向量与入射光向量的夹角越大，接收端所接收到的回波信号强度越弱。并且，在夹角不太大时，回波信号强度随夹角增大而减弱的程度不太明显，但当夹角进一步增大时，回波信号将迅速减弱，最终只剩下漫反射分量。

1.3.5 多径噪声

多径噪声是指在对场景中单个扫描点探测期间，激光接收机除了接收到来自被照射点一次直接反射光外，还接收到了由于漫反射而引起的来自场景中其他物体的多次间接反射光。当存在多径噪声时，激光接收机对光信号的接收情况在数学上可以建模为一次反射光与若干条多次反射光的线性组合［33］为

式中，p0为来自发射激光照射点的一次反射光；pi为由于被照射点的漫反射而来自场景中其他物体的多次反射 光，称为多径干扰项；N为多次反射光的光路数目；叠加了多径噪声后所接收到的光信号。

本文将式（10）中多径干扰项的产生建模为一个随机过程。另外，多径干扰主要是由激光照射到物体表面时发生漫反射而引起，而对于漫反射过程而言，光信号以球面波的形式等强度地朝各个方向辐射出去，因此根据球体的表面积公式，光信号的功率密度将按辐射距离的平方关系快速衰减。本文认为光信号经过较多次数的反射过程后，其能量已经衰减到可以忽略不计（或者说因低于激光接收机的灵敏度而无法被探测到），因此本文认为式（10）中的多径干扰项只包含二次反射光，三次及三次以上的反射光不予考虑。

在存在多径噪声的情况下，本文所仿真得到的一条经过二次反射后最终被激光接收机接收到的光信号强度计算公式为

式中，p0为发射激光照射点的一次反射光强度；diff 为1.3.4 节式（9）中所示的漫反射比率；ak为扫描激光测距系统中当前照射点k的归一化反射率；ai为光路i所对应的二次反射时物体表面的归一化反射率；d1为发射激光照射点将光信号以漫反射的形式反射到场景中其他位置上某物点的过程所经历的距离；d2为场景中其他某物点将光信号以漫反射的形式二次反射到激光接收机所经过的距离。最后，根据多次反射光路相对于一次直接反射光路的光程差，结合光速和时间分辨率计算出相对于一次反射光的时延，并将其在时间轴上延迟相应的时间后，叠加到原直接反射的光信号波形上。

1.3.6 内部噪声

1）光电二极管的退化模型

本文将主要讨论雪崩光电二极管（Avalanche Photodiode，APD）在激光测距系统中的退化模型。但一些光电二极管的特性参数实际上是PIN 光电二极管、APD 和其他类型的光电二极管所共有的（如响应度、响应时间、暗电流和热噪声等），因此接下来所讨论的APD 的退化模型对其他种类的光电检测器件也有一定的参考和指导意义。

APD 的响应度Resp（A/W）定义为入射光所被转换为的电流（又称光生电流）大小与入射光功率的比值，其表达式为［34］

式中，Ip（A）表示光生电流，Pin（W）为APD 的入射光功率。

倍增因子g定义为APD 雪崩放大后的输出电流Im与初始光生电流Ip的比值［35］

光生载流子在耗尽层内的产生、加速和运动，以及APD 的雪崩倍增等物理过程都需要耗费一定的时间，这将导致APD 在接收到光信号后并不会立即输出所转换得到的电信号，而是会有一定的延迟，这个延迟时间就称为APD 的响应时间。

APD 中的暗电流是由器件内部粒子无规则热运动产生的热生载流子在偏压作用下发生漂移而引起［36］。本文将暗电流建模为叠加在回波混沌信号上的加性高斯噪声，其均方值记为

散粒噪声是所有光电探测器件中常见而又不可避免的一种噪声［33］，它将导致实际测得的结果和其期望值之间出现一定的偏差。散粒噪声的均方等效电流可以建模为

式中，q=1.602×10-19C 为单位电荷量常数；Im表示经雪崩倍增后的光电流；B为激光接收机的带宽，本文取混沌激光测距系统中宽带APD 的典型值B=500 MHz。

在APD 的雪崩倍增过程中，载流子与晶体原子发生有效碰撞并电离的随机性将导致增益g的不稳定性［37］，这等效为在所输出的倍增光电流Im中产生了一种噪声波动，这种现象称为过剩噪声，用过剩噪声因子F来表征［35］为

式中，g为式（13）所示的倍增因子；xn为附加噪声指数。

由式（13）可知，输出光电流Im的不稳定性是由不稳定的增益g作用在初生光电流Ip上而造成的，因此这种不稳定性在Im中所体现出来的噪声现象是一种和输入信号本身相关的噪声，这正好符合散粒噪声的特征；另外考虑到扩散电流、产生复合电流和隧穿电流等体暗电流也会参与雪崩倍增过程［37］，故本文将过剩噪声的均方等效电流建模为

2）热噪声

电路中的热噪声不仅存在于光电检测器件中，在整个混沌激光测距系统的各个模块中都存在。系统的热噪声可以建模为均值为零的加性高斯噪声［38］。热噪声与系统的工作温度和负载的等效电阻阻值有关，负载均方热噪声等效电流可建模为

式中，kB=1.38×10-23J ⋅K-1为玻尔兹曼常数；T为APD 的工作温度；RL为负载电阻，本文取典型值RL=1 kΩ。

1.3.7 外部噪声

激光接收机和光电检测器的外部噪声主要来自环境光。外部噪声可以被建模为泊松噪声［37］。本文对激光接收机所接收到的外部噪声Nam建模为

式中，μ为泊松分布的均值；kam为比例系数，用于控制外部环境光噪声的相对强度，即对回波信号信噪比的影响程度。

1.3.8 完整的计算模型

综合本章上述所有对混沌激光测距系统中可能引起激光信号退化的因素的考量与分析，本文最终所实现的基于物理过程的混沌激光测距系统计算模型如图3所示。最后，本文通过MATLAB 软件完成了对如图3所示计算模型仿真程序的设计和编写。

图3 完整的基于物理过程的混沌激光测距系统计算模型Fig.3 The complete computational model of a chaotic laser ranging system based on physical process

2 基于计算模型的深度图重建

如图3所示的计算模型描述了大气衰减、大气湍流、几何衰减、BRDF 效应、多径噪声、APD 的退化模型、热噪声和环境光噪声对混沌激光信号的退化作用，基于此，我们可以生成符合实际情况的场景深度和对应采集值数据对。本文所研究的混沌激光测距系统单次混沌光信号收发过程虽然只能完成对被测场景中单个点的距离值探测，但在实际的应用情景中，如果在激光器的出射口设置一个可通过电信号控制的振镜，即可实现对场景中各点的扫描测距，不同点的测距结果按扫描点的位置顺序排列在一起，就形成了一幅二维的深度图。由于计算模型中各种退化因素会对回波光信号的质量造成不利影响，因此二维深度图中每个点的距离探测结果也将出现误差，最终影响到整幅二维深度图的重建质量。

2.1 混沌信号测距原理

本文采用互相关法测量混沌激光测距系统到被测点的距离。设一维离散混沌序列为xch(t)，将其作为仿真实验中激光发射端的发射信号（即参考信号），则在信号不发生退化的理想情况下，被测物体所反射的回波信号将相对于xch(t)有一个时延τ，记为xch(t-τ)。根据混沌信号的类噪声性，xch(t)与xch(t-τ)的互相关函数应当具有δ函数的性质，并且互相关曲线的尖峰应当出现在t=τ处，即

式中，⊗表示互相关运算；kch为归一化系数。

对式（19）所示的互相关运算结果进行峰值检测，找到互相关曲线峰值所在的时刻τ，即可通过式（20）［8］计算出被测物体的距离d。

式中，c=3×108m/s 为光速；n为大气折射率，取n=1.000 29。

2.2 深度图数据

本文通过3ds max 2018 三维建模软件渲染得到50 张虚拟三维场景的深度图，每张深度图的原始分辨率为512×512，为缩短计算时间，在仿真计算时通过最近邻插值法下采样到32×32。部分场景（#0、#20、#28、#38、#48）的深度图可视化展示于图4。

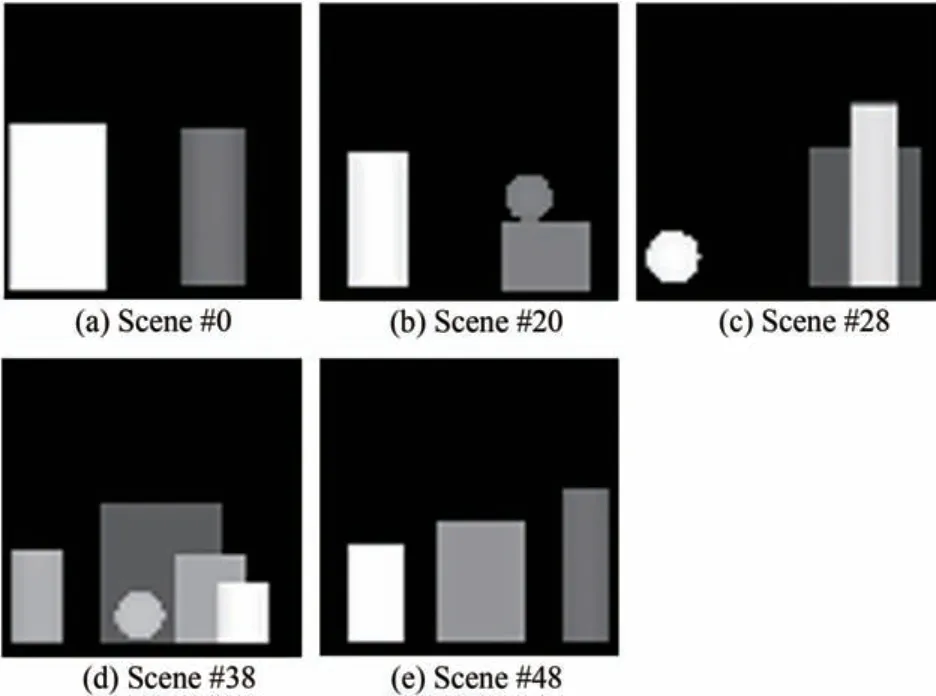
图4 部分合成三维场景的可视化深度图Fig.4 Visualized depth maps of part of the synthetic 3D scenes

在进行仿真实验时，本文首先将所读取到的深度图归一化后乘以30 m，表示深度图中深度值最大的点所对应的实际距离为30 m；深度值为0 的点表示该点没有任何物体，仿真时需要跳过。此外，本文设每张深度图所对应的实际宽度和高度均为30 m。

2.3 深度图重建质量评价因子

本文采用平均峰值信噪比（Peak Signal to Noise Ratio，PSNR）和结构相似性（Structural Similarity，SSIM）两种定量指标作为深度图重建质量的评价因子。其中，PSNR 即峰值信号能量与MSE 之比，其定义式为

式中，MSE 为深度图重建结果与真实值之间的均方误差；MAXVAL 为常数，等于深度图重建任务中所定义的最大可探测深度值。

SSIM 从自然图像高度结构化的特征出发描述了两幅图像imx和imy之间在亮度、对比度和结构3 方面的相似度，其计算式为［39］

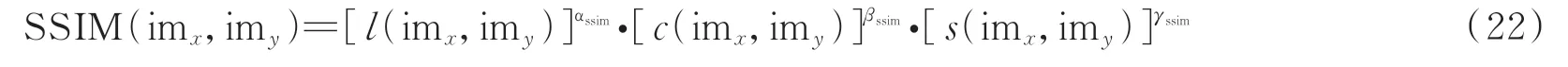
式中，αssim、βssim、γssim为常数，用于调整亮度、对比度和结构3 方面的相似度对最终SSIM 评估值的贡献程度。l(imx，imy)、c(imx，imy)、s(imx，imy)分别表征了两幅图像imx和imy在亮度、对比度和结构3 方面的相似度，其计算式分别为

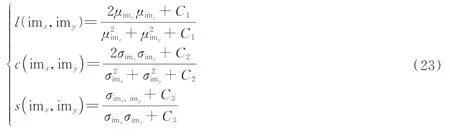
式中，μimx、μimy分别为两幅图像imx和imy的均值；σimx、σimy分别为两幅图像的标准差；σimx，imy为两幅图像的协方差；C1、C2、C3为非零常数，防止分母值较小时导致计算结果不收敛。

2.4 各种退化因素对深度图重建质量的影响

为探究在计算模型中各种可能引起混沌光信号退化并对深度图的重建质量造成不利影响的因素中，哪些影响因素可能会造成相对较大的影响，有重点分析的价值和必要性，本文首先对计算模型中所涉及的各种退化因素的相对影响程度进行了一个简要的分析。

首先，从影响机制方面来考虑，大气衰减、大气湍流、几何衰减、APD 的散粒噪声、过剩噪声、热噪声以及环境光噪声对光信号的退化机制本质上均属于衰减了信号功率或增强了噪声功率，即直接降低了接收端的信噪比。因此，上述影响因素对光信号的退化机制具有一定的相似性，所以选择环境光噪声进行后续研究在一定程度上也体现了不同程度的大气衰减、大气湍流和几何衰减对深度图重建质量的影响。而虽然BRDF 效应的结果也是降低了接收端信噪比，但其降低程度与被测场景中各物体的表面性质有关，即在进行深度图重建时，深度图中每个像素点上的BRDF 效应是不同的；多径噪声被建模为多个相对于原信号在时间轴上延迟不同时间的子信号叠加在原信号上，这与直接在原信号上叠加高斯或泊松噪声有较大区别。另外，多径噪声的存在破坏了飞行时间测距系统中回波信号只经过被照射点的一次直接反射这一基本假设，因此多径噪声可能会为测距结果带来严重的误差［33］。综上，对于BRDF 效应和多径噪声对深度图重建质量的影响，有必要进行单独讨论。

除此之外，本文在除BRDF 效应和多径噪声外的其余各种因素中选择环境光噪声进行后续定量分析的原因还包括如下两点。

1）在实验过程中，考虑到安全和能耗等因素，激光器所能发射的激光能量十分有限，因此环境光的强度可以比现有激光器所能发射激光的能量高很多，特别是在户外环境中，环境光的强度和激光的强度差距将十分悬殊。而大气衰减、大气湍流、几何衰减、APD 的特性参数在实际应用环境中存在一定的合理取值区间，其所引起噪声的强度与信号强度的差距，不容易变得和环境光噪声强度与信号强度的差距那样悬殊。

2）几何衰减和APD 的退化效应与自然环境无关，仅与器件本身的特性有关，因此这些因素所带来的退化效应可以通过人为力量采购更先进的激光器或光电转换器缓解，而无需像环境光噪声那样对自然环境提出要求。

综上所述，本文在后续实验中选择将BRDF 效应、多径噪声和环境光噪声这3 种退化因素对深度图重建质量的影响展开定量研究。各种退化因素对深度图重建质量的影响程度总结于表1。

表1 各影响因素对深度图重建质量的影响程度Table 1 The influence degree of each influencing factor on the reconstruction quality of depth maps

2.4.1 BRDF 对深度图重建质量的影响

保持计算模型里除式（9）中粗糙度krough以外其余各参量不变（取kam=1×10-6，N=20），依次改变krough的值，对各合成深度图进行基于图3所示的计算模型与互相关法的深度图仿真重建实验，其中，计算模型中的所有退化因素均纳入仿真实验过程。在不同的krough下可视化深度图重建结果如图5所示。其中，误差图指各像素点上重建结果与真实值的绝对值误差构成的图像。

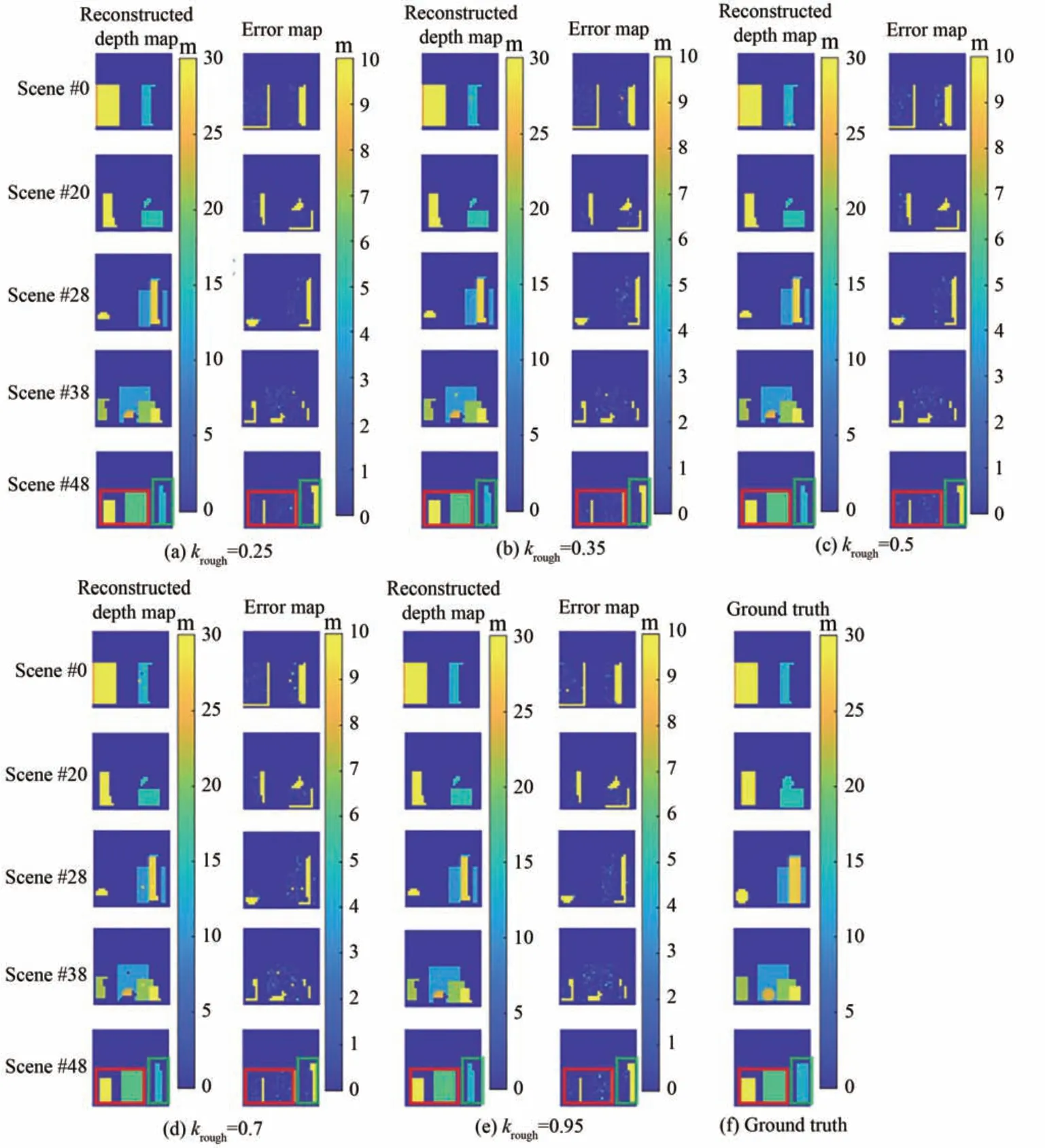
图5 部分场景在不同粗糙度下的可视化深度图重建结果Fig.5 Visualized depth map reconstruction results of part of the scenes under different roughness

由图5可见，在BRDF 效应的影响下，本文所仿真的混沌激光测距系统对具有平整表面且正对激光发射方向的平面能够较好地重建（场景#48 所在行红框部分中的两个长方体），而对于曲面的重建质量较差，特别是对该曲面法向量较大地偏离激光入射方向向量的部分，基本无法重建（场景#48 所在行绿框部分中的圆柱体）。这证明了混沌激光测距系统不擅长重建法向量与发射信号入射方向向量之间夹角较大的物体表面和非平整的表面。

2.4.2 环境光对深度图重建质量的影响

保持计算模型中除式（18）所示的kam以外其余各参量不变（取krough=0.5，N=20），依次改变kam的值，对各合成深度图进行基于计算模型与互相关法的深度图仿真重建实验，同时将计算模型中的所有退化因素纳入仿真实验过程。在不同kam值下的可视化深度图重建结果如图6所示。其中，环境光噪声强度通过信号与环境光噪声平均功率比来表征，单位为dB。

从图6所示的可视化深度图重建结果来看，信号与环境光噪声比分别为13.44 dB 和−46.50 dB 的条件下所重建出的深度图没有较大差异，场景中的物体仍具有较为清晰的轮廓和平滑的表面。但是，当环境光噪声强度系数进一步增大时，深度图的重建质量将迅速下降。这说明本文所仿真的混沌激光测距系统在弱环境光噪声强度时能表现出较好的鲁棒性，但对强环境光噪声较为敏感。另外，进一步观察图5可知，深度值较大的物体（如场景#0 所在行红框部分中的长方体）比深度值较小的物体（如场景#0 所在行绿框部分中的圆柱体）对环境光噪声更加敏感。这是因为在同等强度的环境光噪声强度条件下，光信号经过的距离越长，其为大气衰减、大气湍流、几何衰减等退化因素所造成的信号强度衰减越严重，接收端的信噪比也越低。

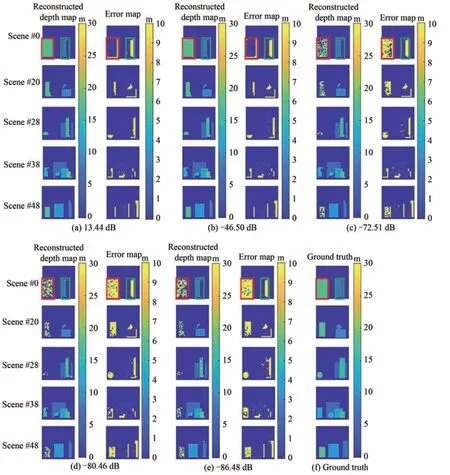
图6 部分场景在不同环境光噪声强度下的可视化深度图重建结果Fig.6 Visualized depth map reconstruction results of part of the scenes under different ambient noise intensity

2.4.3 多径噪声对深度图重建质量的影响

保持计算模型中除多次反射光的光路数目N以外其余各参量不变（取kam=1×10-6，krough=0.5），依次改变N的值，对各合成深度图进行基于计算模型与互相关法的深度图仿真重建实验，计算模型中的所有退化因素均纳入仿真实验过程。在不同N下的深度图重建结果如图7所示。其中，多径噪声的强度定义为添加多径噪声前后的两个信号之间的MSE 之倒数再取对数，单位为dB。

观察图7所示的可视化重建结果可以发现，与2.4.2 小节中图6所示的实验结果有所不同的是，深度值较大物体的重建质量并不会随多径噪声的增强而相比于深度值较小的物体更加迅速地变差，即多径噪声的强度对重建质量的恶化程度和物体的相对深度值大小是无关的。

图7 部分场景在不同多径噪声强度下的可视化深度图重建结果Fig.7 Visualized depth map reconstruction results of part of the scenes under different multipath noise intensity

2.4.4 BRDF、环境光噪声和多径噪声对深度图重建质量的共同影响及其对比

为了更清晰地展示BRDF、环境光噪声和多径噪声对深度图重建精度影响的对比效果，并反映这3 种退化因素对深度图重建质量的共同影响，本节以不同kam，krough和N的条件下深度图重建结果PSNR 和SSIM 值的二维剖面色差图和折线图的形式，对这3 种退化因素对深度图重建质量的共同影响进行了统一的对比，如图8所示。其中，不同kam值下的环境光噪声强度通过信号与环境光噪声平均功率比来表征，单位为dB；多径噪声的强度定义为添加多径噪声前后的两个信号之间的MSE 之倒数再取对数，单位为dB。

观察图8（a）（i-xv，xvi-xx）和图8（b）（i-xv，xvi-xx）可知，在相同环境光噪声和多径噪声强度，不同粗糙度系数的条件下，深度图重建结果的平均PSNR 和SSIM 值基本保持恒定，这说明在混沌激光测距系统中，深度图重建的质量受BRDF 效应中粗糙度系数的影响并不十分明显。但随着粗糙度系数的增大，重建结果的平均PSNR 和SSIM 值略微有下降趋势，这是因为当粗糙度系数增大时，反射信号中漫反射成分逐渐增大（即1.3.5 小节式（11）中的diff 项增大）。而正如1.3.5 小节所述，多径噪声主要是由漫反射效应引起，因此粗糙度系数越大，则多径噪声越强，故而深度图重建质量将有所降低。

此外，观察图8（a）（i-xv，xxi-xxv）和图8（b）（i-xv，xxi-xxv）可知，在相同多径噪声强度和粗糙度系数，不同环境光噪声强度的条件下，本文所仿真的混沌激光测距系统在信号与环境光噪声比由10 dB 数量级逐渐降低到−60 dB 时，深度图重建结果的PSNR 和SSIM 只是随环境光的增强略微有所下降，但当信号与环境光噪声比进一步降低时，深度图的重建质量将迅速下降。为了从直观上体现强度较强的环境光噪声与回波信号波形的强度对比关系，本文还绘制了对同一模拟场景中同一点进行扫描探测时，不同环境光噪声强度下激光信号的时域波形图，如图9所示。

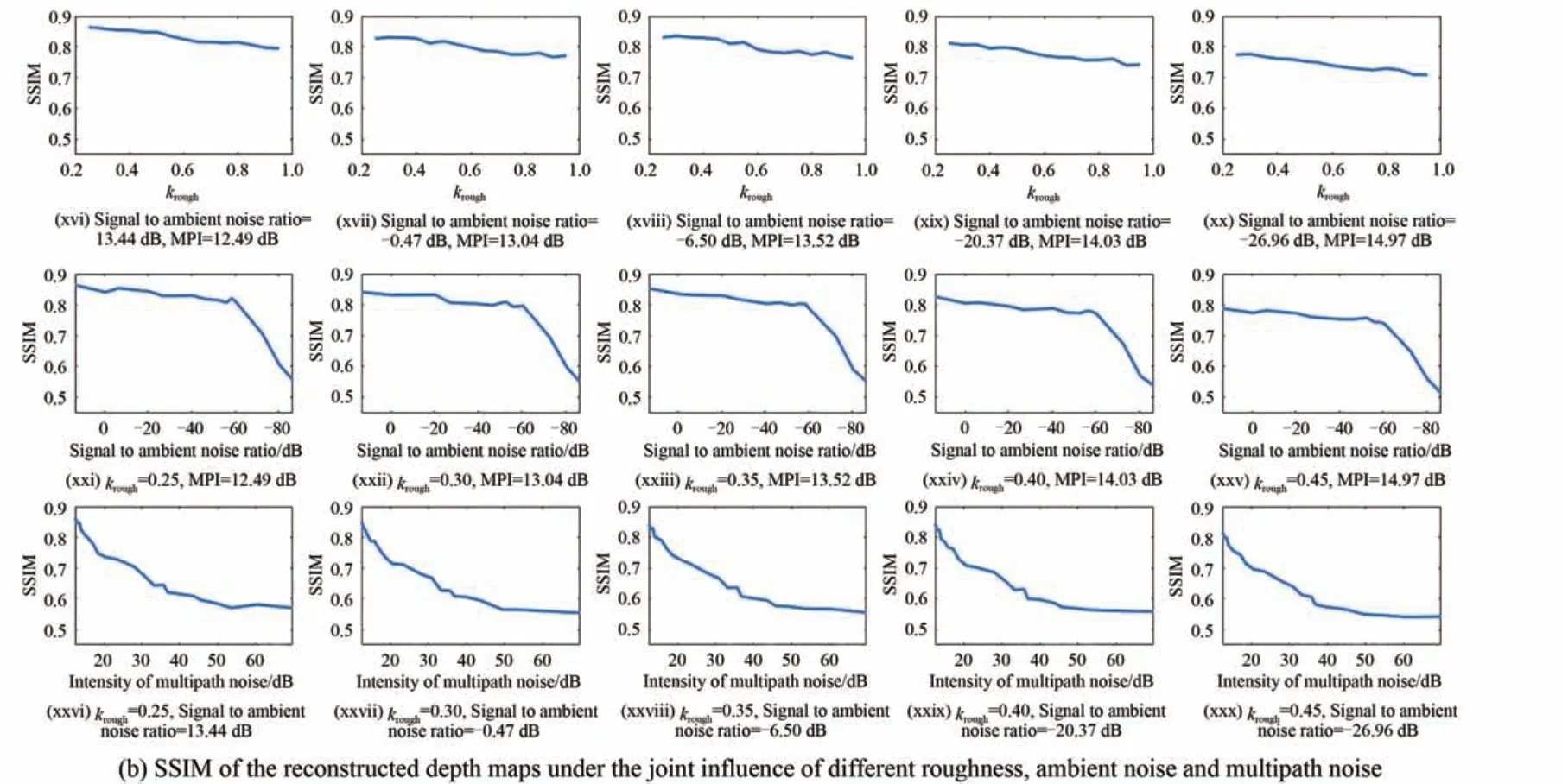
图8 不同粗糙度系数、环境光噪声强度、多径噪声强度共同影响下的深度图重建质量Fig.8 Depth map reconstruction quality under the joint influence of different roughness，ambient noise and multipath noise

结合图9来看，当信号与环境光噪声比降低到−20 dB 以下时，环境光噪声波形的强度已经明显和混沌信号波形相当，信号波形几乎完全淹没在了噪声波形中。而从图7可以看出，在信号与环境光噪声比低至−60 dB 时，深度图重建结果的PSNR 和SSIM 仍然没有明显降低。因此，上述实验结果表明，本文所研究的混沌激光仿真测距系统能够在较大程度上抵抗外部噪声的干扰，表现出对环境光噪声较强的鲁棒性，只有在环境光噪声极强时，混沌激光测距系统才会表现出对噪声的敏感性。

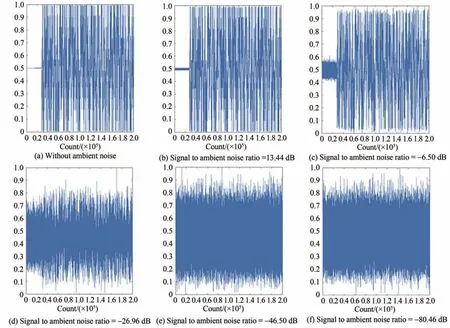
图9 不同环境光噪声强度下激光信号的时域波形图Fig.9 Time-domain waveform of laser signal under different ambient noise intensity

最后，继续观察图8（a）（i-xv，xxvi-xxx）和图8（b）（i-xv，xxvi-xxx）可知，在相同粗糙度系数和环境光噪声强度，不同多径噪声强度下，本文所研究的混沌激光仿真测距模型的深度图重建质量与多径噪声强度（dB）之间的关系，与和环境光噪声强度之间的关系有所不同。在多径噪声强度较弱时，深度图重建结果的PSNR 和SSIM 值随多径噪声的增强迅速衰减，当多径噪声增强到一定程度时，其衰减速率才逐渐趋于平缓。

3 结论

本文从目前缺乏基于完整物理过程的混沌激光测距系统计算模型这一问题出发，提出了一个相对完善的针对混沌激光测距系统的仿真计算模型。该计算模型全面地考虑到了从混沌信号的生成、发射、反射、接收，直至最后信号处理的整个过程中引起混沌信号退化并造成测距误差的各种因素，并通过MATLAB 完成了对该模型的实现、计算和分析。

随后，本文将模拟生成的深度图作为仿真实验中的被测场景，以蔡氏混沌电路模型生成的一维离散混沌序列作为测量信号，对深度图中的各点进行扫描测距，通过互相关法计算各点的深度值。本文着重讨论了BRDF、环境光噪声和多径噪声3 种退化因素对深度图重建质量的影响，以PSNR 和SSIM 两种定量评估指标，计算并可视化展示了在不同退化因素和退化程度的条件下，该混沌激光仿真计算模型所输出的深度图重建结果和重建误差。实验结果表明，本文所研究的混沌激光仿真测距系统的深度图重建质量受BRDF效应中粗糙度系数的影响并不十分明显，但当粗糙度逐渐增大时，漫反射效应将逐渐增强，从而使多径噪声的影响逐渐显现。另外，该仿真测距系统能够在一定的环境光噪声强度范围内表现出对环境光噪声较强的鲁棒性，但对多径噪声较为敏感，即使在多径噪声较弱时，其深度图重建质量也会随多径噪声的增强以较快的速率衰减，当多径噪声增强到一定程度时衰减速率才趋于平缓。因此，在设计实际的混沌激光测距系统时，需要仔细考虑被测物体的光反射性质和多径噪声的影响。

综上所述，本文通过对该基于混沌激光测距系统计算模型的分析讨论，能够为实现实际的混沌激光深度图重建系统、分析影响重建质量的退化因素提供参考和依据，并有助于为机器学习等依赖于大规模数据的算法模型快速高效地构建出基于物理过程且接近于实测环境的混沌激光测距系统深度图探测数据集。