考虑桩周饱和土扰动效应的楔形桩水平振动阻抗
王 珏,项 颖,李振亚,王佳栋,周 叮
(1.河海大学机电工程学院,江苏常州 213022;2.河海大学岩土力学与堤坝工程教育部重点实验室,江苏南京 210098;3.江苏大学土木工程与力学学院,江苏镇江 212013;4.南京工业大学土木工程学院,江苏南京 211816)
引言
楔形桩是一种起源于前苏联的变截面桩基础,它充分利用桩身斜侧面与土体的相互作用,提高了桩侧摩阻力,具有良好的承载性能和经济特性。近年来,国内外学者通过现场或模型试验[1-2]、数值仿真[3]或理论模型[4-5]对楔形桩的承载特性展开了研究,结果表明:在相同土质条件下,楔形桩的单位体积承载力比等截面桩提高0.5~2.5 倍,基础工程造价降低40%~60%,因此楔形桩逐渐被应用于基础工程。对于高耸的动力敏感结构,楔形桩与周围土体的动力相互作用会影响上部结构的动力特性,因此土与楔形桩动力相互作用对上部结构的动力学设计具有至关重要的影响[6]。
在采用子结构法考虑土与结构动力相互作用的动力学建模中,确定反应桩头位移和外力关系的振动阻抗是模拟桩-土动力相互作用的关键。用于模拟土与等截面桩动力相互作用的动力Winkler 模型[7]、平面应变模型[8-9]和连续介质模型[10]等开始被应用于土与楔形桩的动力相互作用问题。蔡燕燕等[11]通过将土与楔形桩沿桩身轴向离散,并利用土体平面应变模型及桩身Euler 梁模型推导了楔形桩桩顶的垂直振动阻抗的解析解。吴文兵等[12]在此基础上进一步考虑了楔形桩的横向惯性效应对垂直振动阻抗的影响。Ghazavi 等[13-14]将Gazetas 等[7]提出的桩侧土刚度和阻尼系数简化公式作为Winkler 地基系数,建立了水平简谐荷载作用下土与楔形桩的动力相互作用模型。杨紫健等[15]在此基础上利用Timoshenko 梁理论进一步考虑了楔形桩剪切效应,计算了桩身位移及内力的包络线。在上述土与楔形桩动力相互作用模型中均视土体为单相介质,随着Biot[16]建立的饱和多孔介质波动理论在桩-土动力相互作用模型中的应用,研究表明:流体在固相中的渗透性会对桩顶振动阻抗产生一定的影响[17-18]。范小雪等[19]基于饱和土平面应变模型研究了非等截面桩的桩身扩径及缩径情况对桩顶水平振动阻抗的影响。因此有必要考虑饱和土中流体渗透特性对楔形桩水平振动阻抗的影响。
此外,上述研究中忽略了桩基础受环境荷载或施工扰动后,桩周土在一定范围内将呈现出径向非均匀性,例如:长期循环荷载影响桩周土弱化,剪切波速降低;受施工影响桩周土压实,剪切波速增加的现象。早期Novak 等[20]就对此提出了将桩周土划分为忽略质量的内部扰动域和半无限大的外部非扰动域的平面应变模型,建立了考虑扰动效应的桩-土相互作用问题的理论基础。为了研究扰动域土体参数呈任意变化形式下的振动问题,研究者们提出了圈层平面应变模型并对此不断完善[21-24],随后被用于研究径向非均质单相土对楔形桩基础振动阻抗的影响。Wu 等[25]基于该模型研究了考虑挤土效应时楔形桩扭转振动阻抗;高柳等[26]基于该模型研究了桩周土压实及弱化情况下的楔形桩垂直振动阻抗;王珏等[27-28]进一步基于Biot 理论及分数导数理论对地基的复刚度传递多圈层平面应变模型进行改进,研究了饱和土压实及弱化效应对楔形桩垂直振动阻抗的影响。上述研究主要针对楔形桩的垂直和扭转振动,但结构在风、波浪或地震作用下,楔形桩通常以承受水平荷载为主,因此求解考虑桩周饱和土扰动效应下的楔形桩水平振动阻抗,对近海工程、高压输电塔、高层建筑等结构的动力学设计具有重要的工程意义。
为了完善上述土与楔形桩动力相互作用的理论模型,本文利用Biot 波动理论建立了饱和土径向复刚度传递多圈层水平振动平面应变模型,推导了考虑扰动效应的桩周土对桩身的水平动反力;基于Timoshenko 梁理论建立了考虑桩身剪切振动效应的横向振动微分方程,利用桩身轴向传递矩阵法推导了桩顶水平振动阻抗的半解析解;参数化研究了楔形角、楔形桩长径比、土体扰动效应以及渗透系数对楔形桩水平振动阻抗的影响。
1 分析模型及基本假定
在如图1所示的含有扰动域的饱和黏弹性半空间中,埋置了一根底面半径为rb,长为L,倾角为θ,顶部受水平及摇摆简谐荷载Q0eiωt和M0eiωt的楔形桩基础。其中,Q0和M0分别为水平和摇摆激振的幅值,ω为激振频率,虚数。如图2(a)所示,将桩-土系统沿轴向从桩顶到桩底划分成M层,其中第i层(i=1,2,…,M)的厚度为hi,该层桩身半径ri0=rb+(M-i)(L/M)tanθ。为了处理桩周饱和土的扰动效应,如图2(b)所示,将各层桩周土径向离散成宽度为Δri的内圈扰动域及外圈非扰动域,并进一步将内圈扰动域径向离散成N个子圈层,由内至外标号为1,2,…,N,非扰动域标号为N+1。因此,第i层中第j圈的外半径rij表达式为rij=ri0+jΔri/N。当各薄层土中扰动域的径向子圈层单元划分足够多时,可近似将子圈层中的饱和土视为均质。
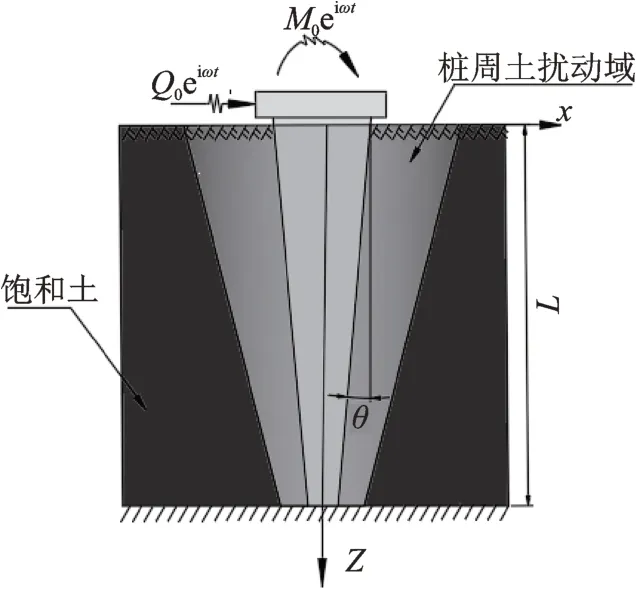
图1 受扰动的饱和土与楔形桩水平动力相互作用Fig.1 The disturbed saturated soil interacts with the wedge pile horizontally
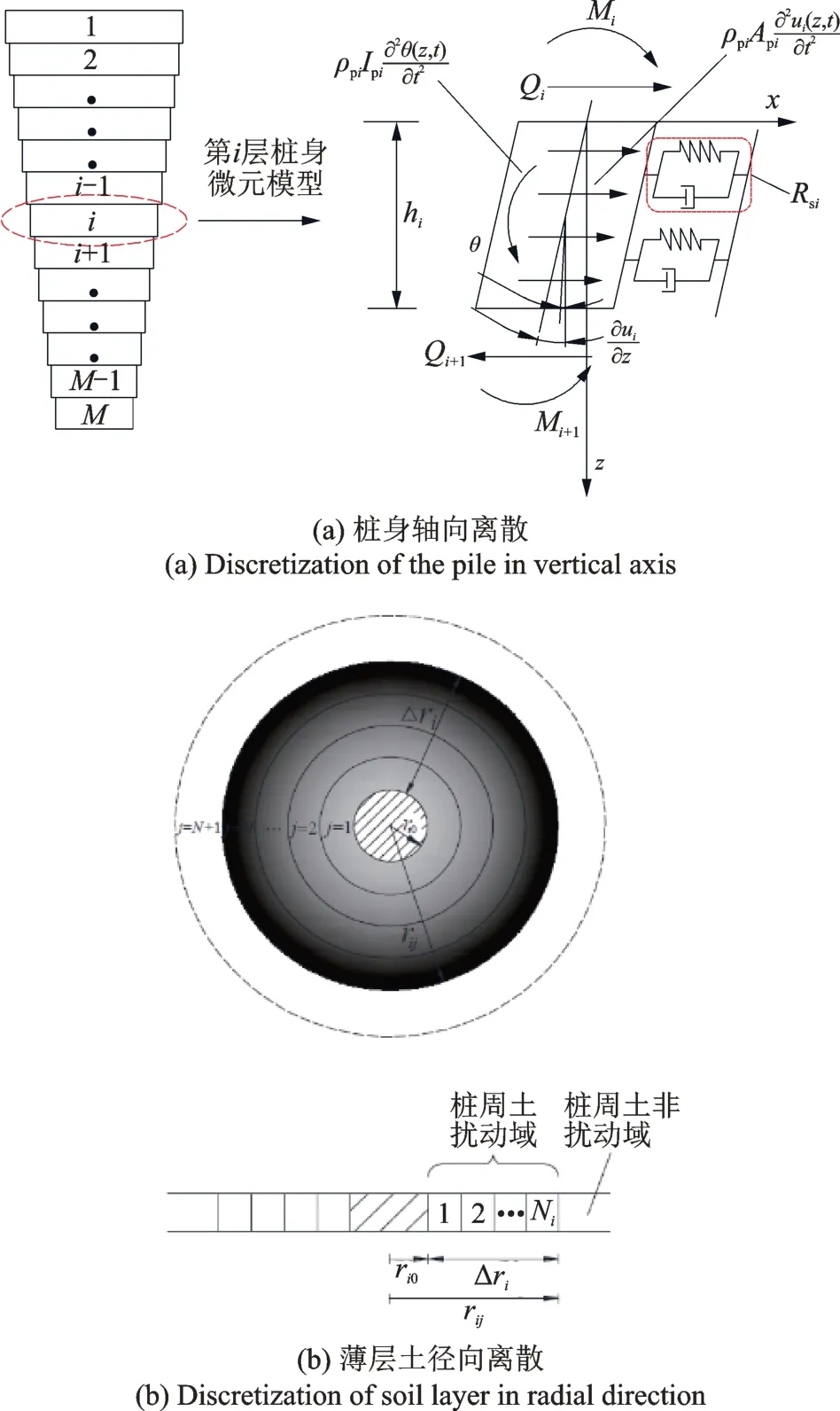
图2 桩-土动力相互作用系统离散模型Fig.2 The discrete model of the pile-soil dynamic interaction system
模型中的基本假定如下:地基土轴向由一系列满足Novak 平面应变模型的土层组成。各层桩身视为等截面Timoshenko 梁。系统振动过程中桩-土系统满足弹性和小变形假定,相邻子圈层交界面及相邻桩身交界面均满足力的平衡及位移连续条件。
2 方程建立及求解
2.1 饱和土的水平振动
取第i薄层土中第j圈内的饱和土单元为研究对象,基于Biot 理论描述的平面应变模型,各饱和薄层土的水平振动控制方程为:

引入如下势函数,令:

式中φ1和φ2分别为饱和土固相和液相的位移标量;φ1和φ2分别为固相和液相的位移矢量。
将式(2)代入式(1),做Laplace 变换后整理得两个含有微分算子的矩阵方程。为使方程有非零解,则需满足下式:
式中
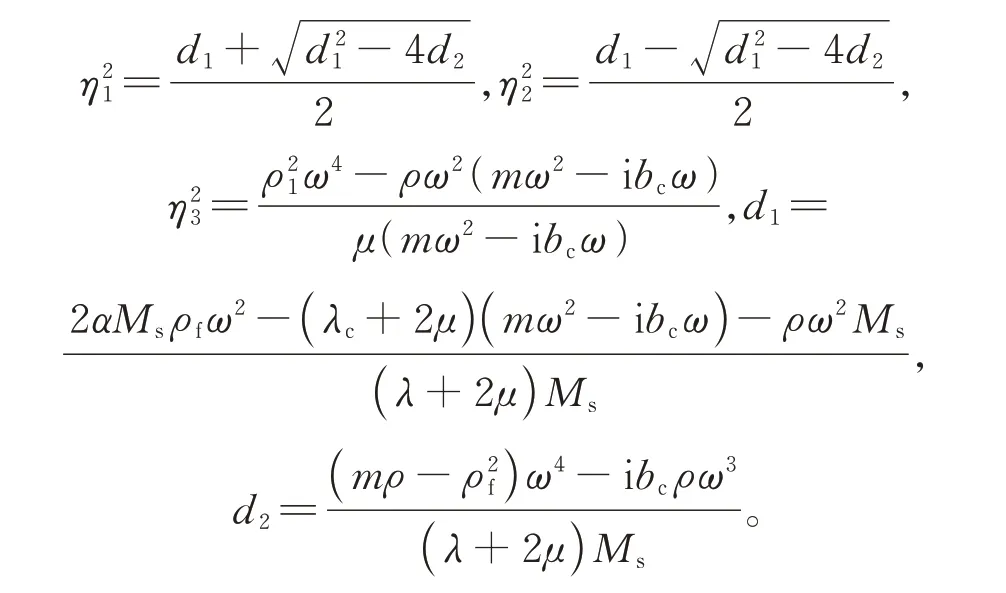
由算子分解理论及分离变量法可得式(3)和式(4)中φi和φi(i=1,2)的解,进而代入式(2),得到固相径向位移ur,固相环向位移uθ,液相径向位移wr,以及液相环向位移wθ的通解,并表示成如下形式:
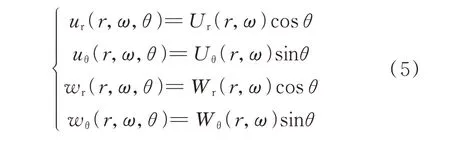
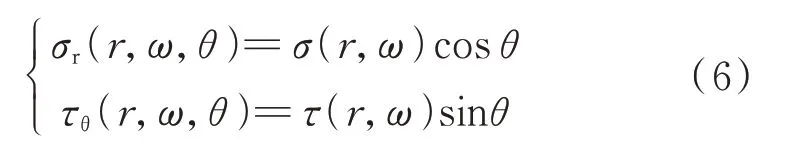
将式(5)和式(6)中的位移和应力通解表示成如下矩阵表达式:
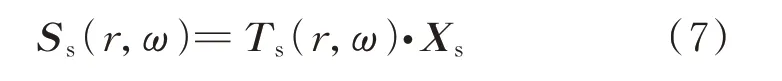
式中 位移和应力向量Ss={UrUθWrWθσ τ}T,待定系数向量Xs={AsBsCsDsEsFs}T需根据土体边界条件求解,饱和土的径向传递矩阵Ts的表达式见附录A。
扰动域内的解(r≤rN)
对扰动域中第j圈层(j=1,2,…,N)饱和土,根据式(7)中的位移场和应力场通解有:

式中Tsj(r,ω)为将第j圈内的饱和土材料参数代入附录公式(A-1)计算得到的该圈层土体传递矩阵。
根据交界面的位移和应力连续条件Ssj(rj,θ)=Ss(j+1)(rj,θ),由传递矩阵法可建立第1 层土体待定系数向量Xs1和第N层土体待定系数向量XsN之间的关系:
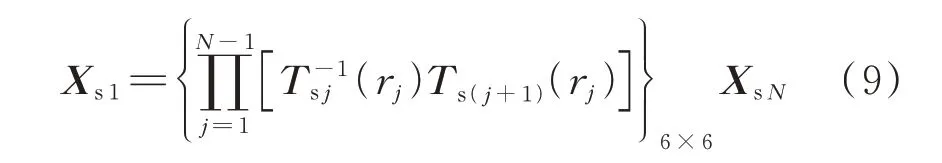
非扰动域内的解(r≥rN)
对于第N+1 圈的饱和土非扰动域,其径向需满足无限域的边界条件。因此,待定系数向量Xs(N+1)中的系数As=Cs=Es=0。根据式(7)中非弱化域饱和土位移场和应力场通解有:
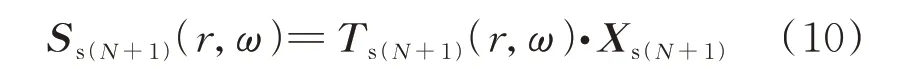
式中Xs(N+1)={BsDsFs}T,Ts(N+1)(r,ω)为将非扰动域饱和土材料参数代入附录A 公式(A-2)计算得到土体传递矩阵。
薄层土与桩身接触面的水平动反力
根据扰动域和非扰动域交界面连续条件SN(rN,θ)=SN+1(rN,θ),采用传递矩阵法可建立第1 层土体待定系数向量Xs1和第N+1 层土体待定系数向量Xs(N+1)之间的关系:

根据桩周土边界条件,当桩身段发生单位水平位移且桩体接触面不透水时,由下式可确定第1 圈层位移场和应力场通解中的待定系数:

将求解得到的第1 圈层待定系数式(12)代入式(7)后,即得第1 圈层中应力场σr(r,θ)和τθ(r,θ)的解,对桩周土r=ri0处的应力解积分,则可得桩-土接触面上单位位移产生的水平动反力:
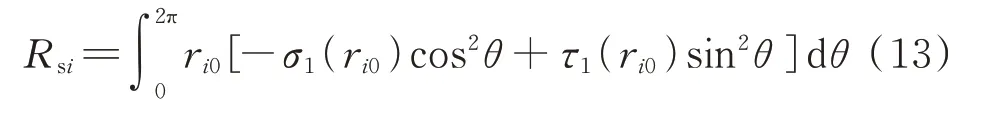
2.2 楔形桩的水平振动
根据Timoshenko 梁振动理论,在第i层桩侧土动反力作用下,桩身横向振动位移upi(z,t)满足以下振动控制方程:

式中κ为桩身截面形状系数;Api,ρpi,Epi,Gpi和Ipi分别为第i层桩身截面积、密度、弹性模量、剪切模型和截面惯性矩。
当桩身受简谐荷载作用时,其横向振动位移满足upi(z,t)=Upi(z)eiωt形式,式(14)可整理成关于位移的四阶常系数微分方程,其通解为:
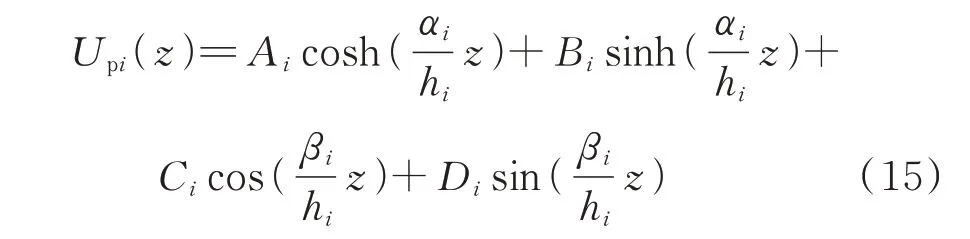
式中
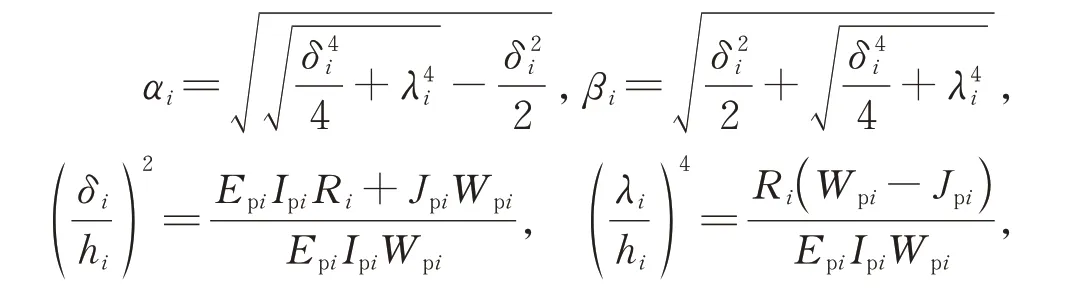
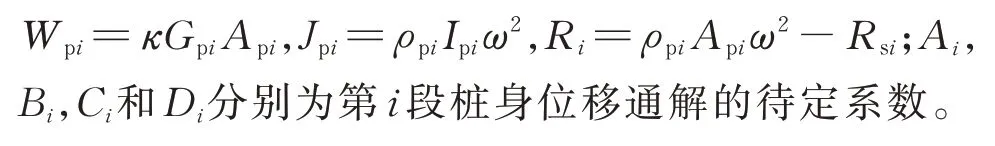
将式(15)代入桩身截面转角、截面弯矩以及截面剪力的微分关系,整理后可得第i段桩身单元的变形、内力与待定系数之间的关系为:
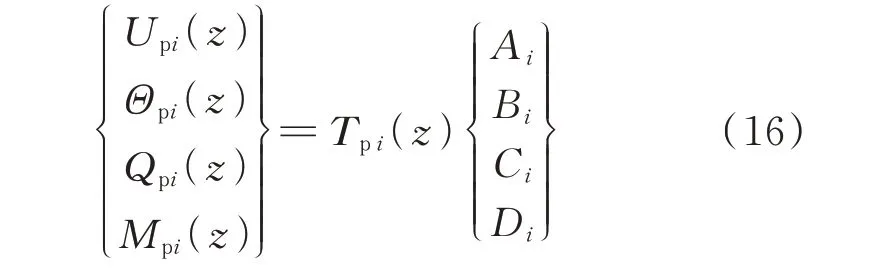
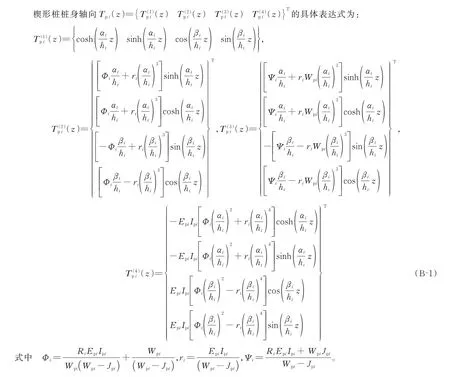
式中Tpi(z)为桩身的轴向传递矩阵,其表达式见附录B。
根据式(16)并结合桩身横向振动时力与变形的微分关系,可建立第i层桩段的上下表面变形和内力的关系如下:

根据相邻桩身界面连续性条件,可通过轴向传递矩阵法建立楔形桩桩顶、桩底之间位移和力的关系:
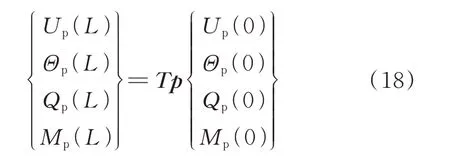
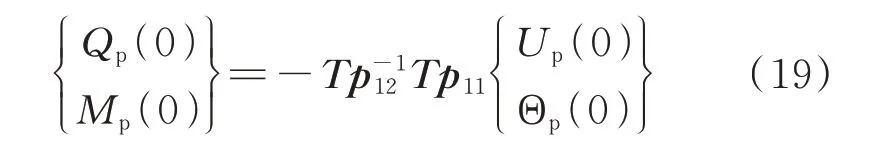

式中Khh表示水平阻抗无量纲化之后的动刚度;Chh表示水平阻抗无量纲化之后的动阻尼。
3 算例分析
以下算例通过参数分析研究了桩身的楔形角和剪切效应,以及桩周土的扰动效应及流体渗透性对楔形桩水平振动阻抗的影响。如无特殊说明,根据文献[19]中的饱和土与桩身计算参数取值如下:L=10 m,rb=0.5 m,Ep=30 GPa,ρp=2500 kg/m3,Es=30 MPa,ρf=1000 kg/m3,ρs=2700 kg/m3,kD=10-6m/s,n=0.4,vs=0.3,α=0.99,Ms=4.9 GPa,βs=0.0。剪切模量Gs=0.5Es/(1+vs),剪切波速Vs=(Gs/ρs)1/2,楔形桩的倾角为θ=1°。此外,在分析过程中将频率通过桩底半径rb及非扰动域剪切波速Vs进行无量纲化,令a0=ωrb/Vs。通过对楔形桩桩身单元轴向划分单元数及桩周饱和土扰动域径向划分单元数的收敛性计算分析,以下算例中轴向和径向的离散单元数分别取M=30 和N=30。
3.1 楔形角对水平振动阻抗的影响
图3 为不同桩身楔角对水平振动阻抗的影响,在桩底半径和桩长不变的前提下,桩身楔角取为0°~3.0°。当楔形角θ=0°时,即退化为饱和土中的直桩,由图3 可见,通过与文献解的对比,其结果表现出较好的一致性。此外,从图3 中可以看出:当无量纲激振频率较小(0≤a0≤1.0)时,水平动刚度会随着楔形角的增大而增大,数值计算表明最大提高了2.5 倍左右。随着频率的提高,楔形桩的水平振动阻抗会随频率的改变而产生波动,且楔形角越大频率依赖性越强。因此在对楔形角较大的桩基础进行动力学设计时,需要结合外激振荷载的特征频率进行综合考虑。
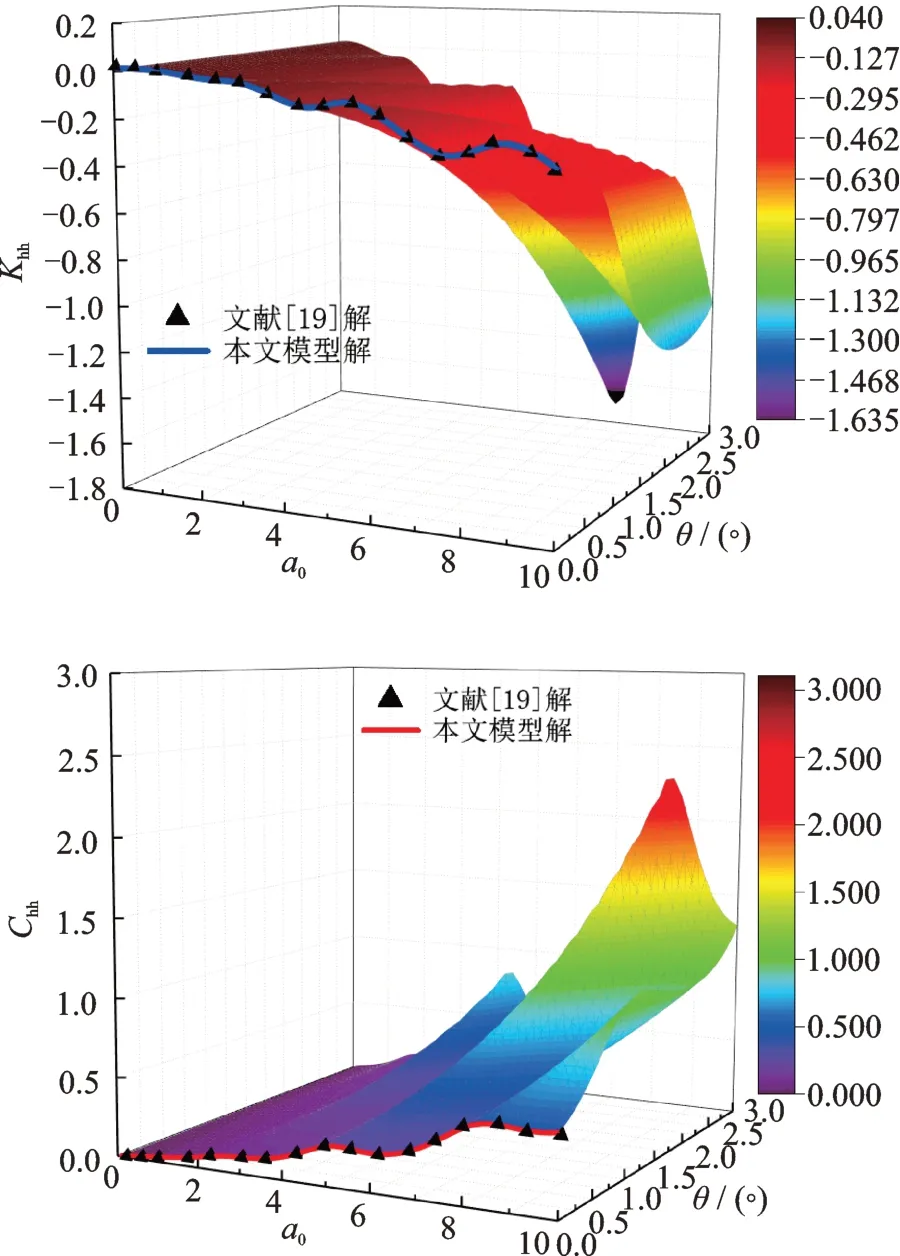
图3 埋置于饱和土中的楔形桩水平振动阻抗Fig.3 Lateral vibration impedance of wedge pile embedded in saturated soil
3.2 饱和土扰动效应对水平振动阻抗的影响
桩周饱和土的不同扰动程度采用桩-土界面剪切模量GSi与非扰动域土体剪切模量GSo的比值表示,扰动域中内外侧的土体剪切模量呈线性变化。当GSi/GSo<1 时表示桩周土发生弱化;当GSi/GSo=1时表示桩周土不发生扰动作用;当GSi/GSo>1 时表示桩周土被压实。为验证本文考虑扰动效应的土体模型推导及程序的正确性,如图4所示将饱和土退化为单相介质,与文献[21]中考虑单相土扰动效应的桩顶水平振动阻抗解进行对比,其中阻抗系数αhh和βhh采用文献[21]中的表达式Rhh=Ks(αhh+ia0βhh)进行了规格化,Ks为当无量纲频率为0 时楔形桩的静刚度。从图4 可以看出,将本文饱和土退化为单相介质后的计算结果与文献解具有较好的一致性。
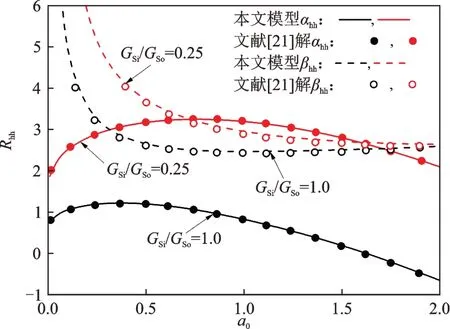
图4 考虑单相土扰动效应下的桩顶水平阻抗对比Fig.4 Comparison of lateral impedance of pile tip under single-phase soil disturbance is considered
桩周饱和土不同扰动程度对楔形桩水平振动阻抗的影响如图5所示,通过与非扰动地基情况下的桩顶阻抗解对比可以看出:在低频时随着桩周土弱化程度增加,楔形桩的动刚度减小,但低频振动时该弱化程度对楔形桩水平振动阻抗的影响并不大,此时可以忽略桩周土的扰动效应。随着激振频率的增加,水平振动阻抗随频率的增大而发生波动,其中桩周土共振效应会随着桩周土的压实而减小。桩周土的不同扰动范围(Δri/ri0)对楔形桩水平振动阻抗的影响如图6所示。由于在工程上扰动的范围通常不会超过桩半径的1.5 倍,因此扰动范围分别取桩身半径的0.5,1.0,1.25 及1.5 倍四种情况进行分析,从图6 中可以看出:在扰动程度GSi/GSo不变的情况下,桩周土扰动范围的扩大对楔形桩水平振动的影响并不显著。
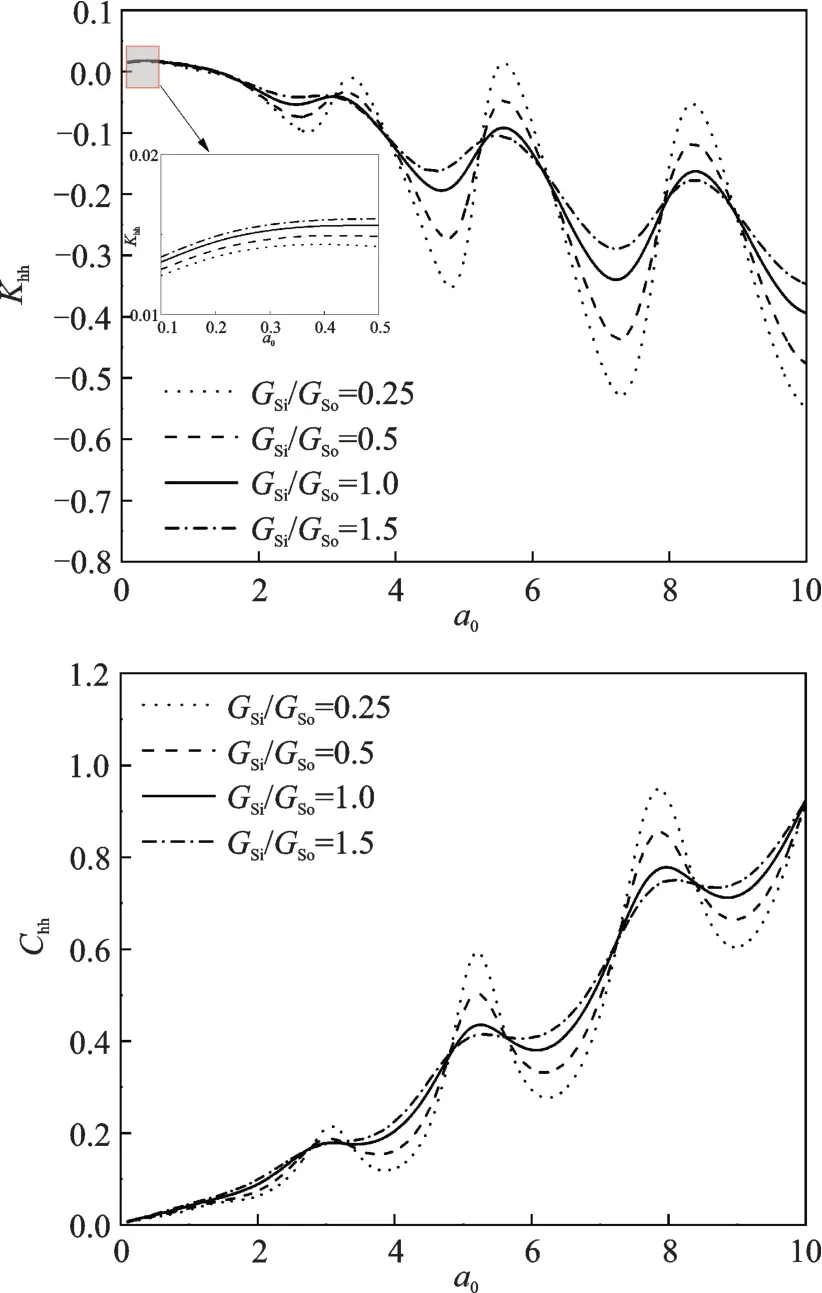
图5 不同扰动效应下桩顶阻抗随无量纲频率的变化Fig.5 The variation of pile top impedance with dimensionless frequency under different disturbance effects
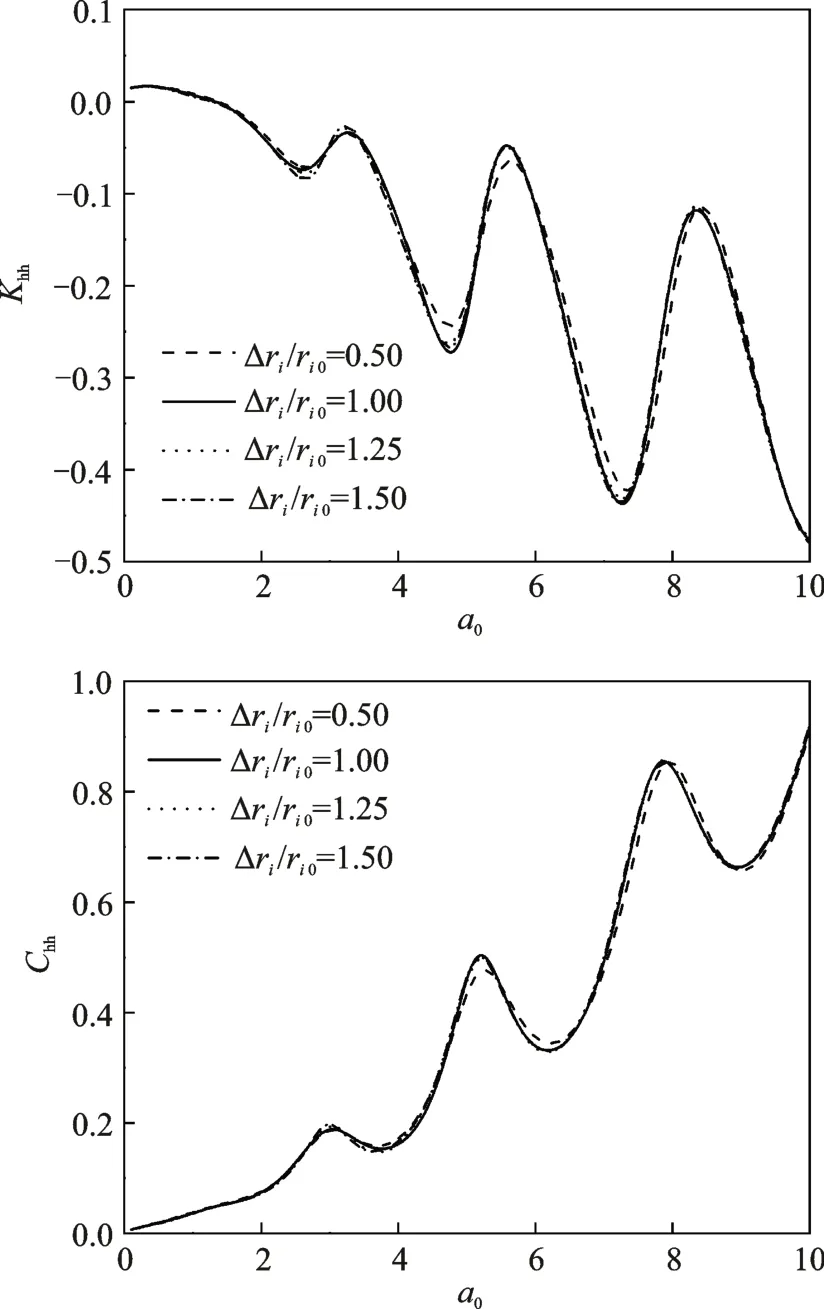
图6 不同扰动范围下桩顶阻抗随无量纲频率的变化Fig.6 The variation of pile top impedance with dimensionless frequency under different disturbance range
这里需要说明的是本模型实现了考虑饱和土扰动效应的楔形桩水平振动阻抗计算,参数化分析了扰动效应中饱和土剪切模量对阻抗的影响。但实际工程中扰动效应在改变土体剪切模量的同时也会引起孔隙率和渗透性等参数的改变,有必要进一步通过饱和土循环加载试验得到真实的土体参数后代入模型计算,分析考虑多参数耦合变化对桩顶阻抗函数的影响。
3.3 流体渗透性对水平振动阻抗的影响
本算例如图7所示讨论了饱和土中达西渗透系数kD对楔形桩水平振动阻抗的影响。从图7 中可以看出:当渗透系数小于1×10-4m/s 时,渗透系数对桩顶水平阻抗几乎没有影响,这是由于渗透系数过小时,土体中液体的流动受到限制,土体趋近于单相土的封闭系统,此时可以采用单相土理论进行简化计算。但是,当土体的渗透系数大于1×10-4m/s时,随着渗透系数的提高,对桩顶水平阻抗的影响越显著。当施工场地条件为以砂砾、粗砂等渗透系数大的地基土为主时,如采用单相介质模型分析,会因忽略了振动过程中饱和多孔介质内流体的惯性效应而影响水平振动阻抗计算的合理性。除了地基土颗粒自身特性外,扰动效应也会改变饱和土的渗透系数,例如压实效应会导致土的密度增加,孔隙减小,渗透性也会降低,从而影响楔形桩水平振动阻抗。因此,这时有必要考虑渗透系数对桩顶阻抗的影响。

图7 不同渗透系数下水平阻抗随无量纲频率的变化Fig.7 The variation of lateral impedance with dimensionless frequency under different permeability coefficients
3.4 桩身剪切效应对水平振动阻抗的影响
本算例分别采用Timoshenko 梁和Euler 梁理论计算了如图8所示的不同激振频率下桩顶水平振动阻抗随桩身长径比的变化。为了便于控制变量分析,本算例θ取为0°。从图8 中可以看出:当激振频率较低时,桩顶刚度随着长径比L/d的增加而减小,最后趋于一个定值,此时的长径比称为有效桩长。桩身在低频振动时主要受剪切效应的影响,在长径比较小时采用Timoshenko 梁模型计算的动刚度比Euler 梁模型的结果偏小,但随着长径比增大,当L/d>5 时两种模型的计算结果差异小于5%。当激振频率较大时,桩顶动刚度和动阻尼随桩径比的变化存在一定的波动,但最后趋近于定值,此时的有效桩长比激振频率较小时的有效桩长大。在频率较大时,剪切变形和转动惯量对于动阻尼的影响不大,但对动刚度的影响不可忽略,从桩径比随动刚度变化的图可以看出,即使L/d达到20 时,两种模型的动刚度依然存在差异,且振动频率越大差异越大,这是由于随着振动频率增大,桩身转动惯量的影响会更显著。因此,对于高频振动下长径比较小的楔形桩,采用考虑桩身剪切变形和转动惯量的Timoshenko梁理论能提高水平振动阻抗的计算精度。

图8 不同桩身模型下桩顶阻抗随长径比的变化Fig.8 The variation of pile top impedance with slenderness ratio under different pile models
4 结论
本文利用Biot 波动理论建立了考虑扰动效应的饱和土复刚度传递多圈层水平振动平面应变模型,利用Timoskenko 梁理论及传递矩阵法建立了楔形桩横向振动模型,推导了考虑桩周土扰动效应下的桩基水平阻抗半解析解。通过对比算例验证了本文理论推导和数值计算的合理性,并参数化分析了楔形角、桩周土扰动效应、达西渗透系数及桩身剪切效应对楔形桩水平振动阻抗的影响,结论如下:
(1)在低频激振下,增大楔形角能提高桩顶的水平阻抗;随着振动频率提高,增大楔形角会提高阻抗的频率依赖性。因此对于楔形角较大的桩基进行动力学设计时要综合考虑外激振荷载的特征频率。
(2)桩周土的扰动效应对楔形桩水平振动阻抗的影响主要集中在其随频率变化曲线的共振峰值处。桩周土的弱化在低频振动时会降低楔形桩的水平阻抗,随着振动频率的增加,弱化效应会提高水平振动阻抗的共振幅值。
(3)当流体渗透系数较小时,液体流动受限,土体趋近于封闭系统,此时渗透系数的减小对桩顶水平阻抗几乎没有影响。但当场地土以渗透系数较大的砂砾和粗砂等地基条件为主时,有必要考虑土体中流体惯性效应对楔形水平振动阻抗的影响。
(4)通过Timoshenko 梁与Euler 梁模型的计算结果相比表明,桩身剪切效应对于水平阻抗的实部刚度影响较大而对其虚部阻尼影响较小。当长径比较小时采用Timoshenko 梁模型计算的动刚度比Euler 梁模型的结果偏小。对于低频振动,当长径比L/d>5 时两种模型的计算结果差异小于5%。但对于高频振动,即使L/d>20 时依然有必要采用Timoshenko 梁理论描述桩身的横向振动。
附录A:饱和土径向传递矩阵
扰动域(r≤rN)内第j圈层(j=1,2,…,N)的土体传递矩阵表达式为:
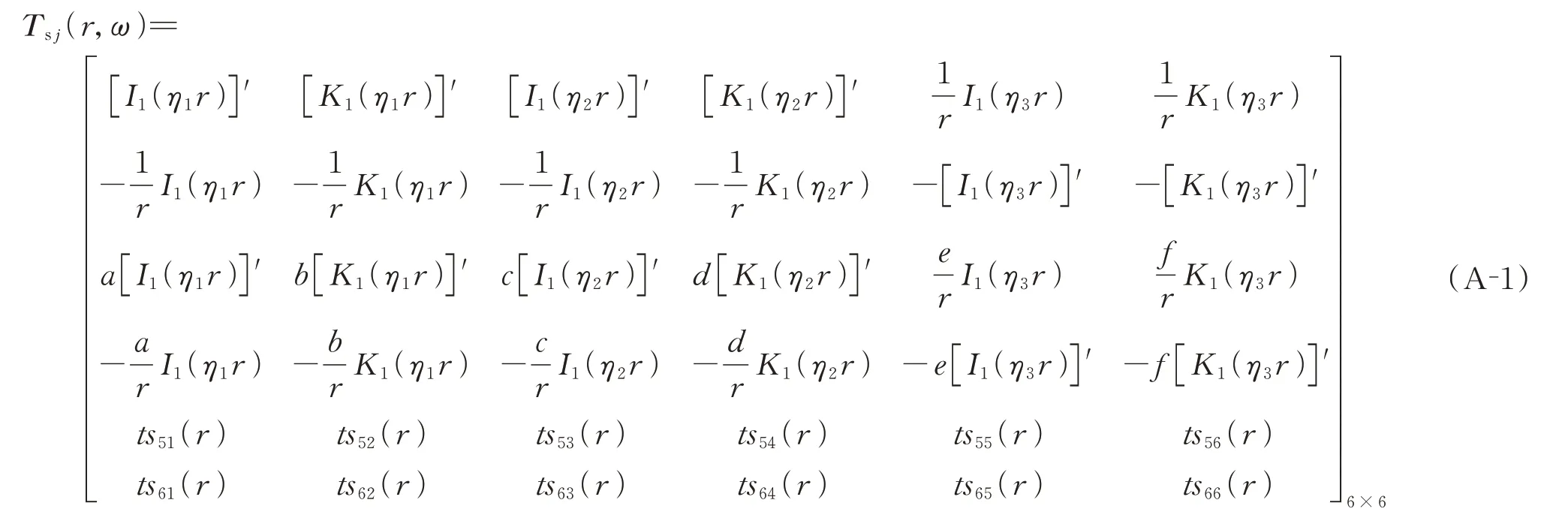
上述矩阵中的第5 和6 行元素表达式如下:
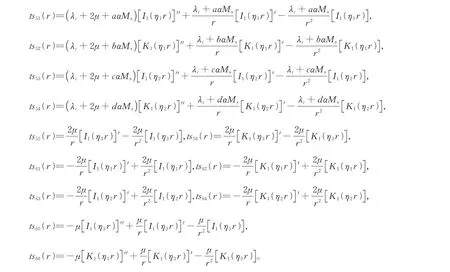
式中K1()和I1()分别为第一类和第二类一阶虚宗量贝塞尔函数;[]′和[]′′分别为对径向r的一阶和二阶求导运算符号。相关系数满足:。
第N+1 圈层的非扰动域(r≥rN)内的土体传递矩阵表达式为:


附录B:桩身轴向传递矩阵