Anti-noise performance of the pulse coupled neural network applied in discrimination of neutron and gamma-ray
Hao-Ran Liu• Zhuo Zuo,3• Peng Li• Bing-Qi Liu • Lan Chang,3 •Yu-Cheng Yan,3
Abstract In this study, the anti-noise performance of a pulse-coupled neural network (PCNN) was investigated in the neutron and gamma-ray(n-γ)discrimination field.The experiments were conducted in two groups.In the first group,radiation pulse signals were pre-processed using a Fourier filter to reduce the original noise in the signals,whereas in the second group,the original noise was left untouched to simulate an extremely high-noise scenario. For each part, artificial Gaussian noise with different intensity levels was added to the signals prior to the discrimination process.In the aforementioned conditions, the performance of the PCNN was evaluated and compared with five other commonly used methods of n-γ discrimination:(1)zero crossing,(2)charge comparison,(3)vector projection,(4)falling edge percentage slope,and(5)frequency gradient analysis.The experimental results showed that the PCNN method significantly outperforms other methods with outstanding FoM-value at all noise levels.Furthermore,the fluctuations in FoM-value of PCNN were significantly better than those obtained via other methods at most noise levels and only slightly worse than those obtained via the charge comparison and zerocrossing methods under extreme noise conditions. Additionally,the changing patterns and fluctuations of the FoMvalue were evaluated under different noise conditions.Hence,based on the results,the parameter selection strategy of the PCNN was presented. In conclusion, the PCNN method is suitable for use in high-noise application scenarios for n-γ discrimination because of its stability and remarkable discrimination performance. It does not rely on strict parameter settings and can realize satisfactory performance over a wide parameter range.
Keywords Pulse coupled neural network ∙Zero crossing ∙Frequency gradient analysis ∙Vector projection ∙Charge comparison ∙Neutron and gamma-ray discrimination ∙Pulse shape discrimination
1 Introduction
Given that the demand for neutron detection has significantly increased in recent years,neutron monitoring has become vital in numerous fields such as deep-space exploration [1], reactors [2, 3], radiopharmaceuticals [4],geology [5], national security [6, 7], and meteorology [8].One of the essential challenges in neutron detection is the presence of accompanying gamma-rays. They are generated by the interaction, i.e., inelastic scattering and radiation capture, between the neutrons and the surrounding environment. Hence, typically, an extensive gamma background is present wherever neutrons exist [9]. For most radiation detectors, the incident neutrons and gamma-rays are simultaneously recognized, and it is difficult to differentiate the signal coming from neutrons or gamma-rays.To distinguish these signals,pulse-shape discrimination(PSD)was developed [10, 11], which is based on the differences in [12] the shapes of neutrons and gamma-rays pulse signals (n-γ PSs). Therefore, discrimination techniques rely heavily on scintillator materials, and many scintillators with cutting-edge discrimination performance have been developed [13–15]. It should be noted that most organic scintillators exhibit similar decay characteristics, but other scintillators exhibit different characteristics such as CLYC.Among PSD-capable scintillators, plastic scintillators are more commercially friendly, convenient to transform, and adaptive to different work conditions; however, their discrimination capabilities are limited.Conversely,liquid and crystal [16] scintillators commonly outperform plastic scintillators in terms of discrimination, although they are more expensive. Furthermore, liquid scintillators are difficult to store and transport.
Plastic scintillators are preferred in many scenarios due to their application requirements and cost control. However, many broadly used discrimination methods, such as charge comparison[17]and the zero-crossing method[18],perform poorly in plastic scintillators when compared to liquid scintillators. Consequently, a discrimination method capable of realizing a higher performance in plastic scintillators is required. In 2021, Liu et al. resolved this problem by proposing a pulse-coupled neural network(PCNN)-based discrimination method [19], which exhibits a remarkable discrimination effect when applied to n-γ PS data acquired for a plastic scintillator. This method can recognize dynamic information inside n-γ PSs and has the advantage of no pre-training process requirements. Furthermore, the anti-noise ability was mentioned in their study, but they did not further validate the anti-noise performance of the PCNN applied in n-γ discrimination.
Although many studies have been performed to control the noise in various detection systems[20–22],it is still an inevitable problem in any radiation detection system;hence,it is crucial for discrimination methods to maintain a stable performance under the influence of noise. In the present study, experiments were conducted to investigate the noise immunity of the PCNN.The n-γ mixed field,used in the study, was generated by a 4.5-MeV (mean energy)241Am-Be neutron source, and n-γ PSs were measured from this field via an EJ299-33 plastic scintillator and a 9821B photomultiplier. Different levels of Gaussian noise were added to the pulse shapes prior to the discrimination process. The experimental results of the PCNN were compared with the other five commonly used discrimination methods under different noise conditions,namely,zero crossing (ZC), charge comparison (CC), vector projection(VP),falling edge percentage slope(FEPS),and frequency gradient analysis (FGA) methods. Additionally, the influence of the PCNN parameters on its anti-noise effect was elucidated. Based on this, a parameter decision strategy was presented for high-noise application scenarios.
The remainder of this paper is organized as follows. In Sect. 2, several n-γ discrimination methods are introduced. In Sect. 3, evaluation criteria for n-γ discrimination are defined. In Sect. 4, details of the experimental design and results are presented, and the characteristics of the PCNN parameters are analyzed.Finally,conclusions of this study are presented in Sect. 5.
2 Principles of discrimination methods
2.1 Zero crossing
The zero crossing (ZC) method is one of the most used methods in the n-γ discrimination field based on a simple methodology, while it offers reliable discrimination results[18,23].To discriminate the pulse signals using this method,n-γ PS must be first transformed into a bipolar pulse signal.Second,the so-called zero-crossing time should be calculated by finding the time interval between the beginning of the n-γ PS and zero-crossing point of the bipolar pulse signal,which are set as 10%of the pulse maximum and the first sample after the pulse’s peak that crosses the baseline, respectively.Finally,the neutrons and gamma-rays can be discriminated by comparing the zero-crossing times of different n-γ PSs.Specifically, a digital CR-RC2filter was used for the transformation from the original n-γ PS to the bipolar pulse signal,whose mathematical expression is as follows[24]:

where τ=RC denotes the shaping time and T denotes the sampling interval of the pulse signal.Furthermore,τ and T were determined using the detection system and its settings. Given the slower decay speed of neutron pulse signals (organic scintillators), the zero-crossing time of neutrons is longer than that of gamma-rays.
2.2 Charge comparison
As the charge comparison (CC) method exhibits outstanding discriminating efficiency and stability,it has been widely used in many areas that require the n-γ discrimination technique[17].A criterion termed as charge ratio Rcis used to transmit the pulse shape information of neutrons and gamma-rays, which can be calculated as follows [25]:

where QNdenotes the charge of the slow component,which can be calculated by integrating the amplitude of the falling edge and delayed fluorescence parts of a pulse signal,QMdenotes the charge of the entire signal,which is defined as the amplitude integration of all sampling points of a given pulse signal. Given that the decay speed of a pulse signal generated by a neutron is slower than that of a gamma-ray photon, along with the effect of the delayed fluorescence that is characteristic of neutron pulses, the slow component charge QNdue to neutrons is significantly larger than that of gamma-ray signals.Hence,the Rc-value for the neutrons is higher than that for the gamma-rays because of the differences between the n-γ PSs.
2.3 Vector projection
In the vector projection(VP)method[26,27],the pulse signals of different particles are considered as vectors pointing in different directions in a vector space.First,n-γ PSs were normalized. Second, two ideal pulse signals corresponding to neutron and gamma-rays are defined.They are typically obtained by averaging a significant number of respective n-γ PSs. Then, every single vector(i.e.,n-γ PS)is projected in the projection direction,which is defined as the difference between ideal pulses. The projection results of neutrons and gamma-rays differ and act as the discrimination factor. The projection results of neutrons are generally larger or smaller than those of gamma-rays based on whether the projection direction is positive or negative with respect to the vector space.In this study, the projection results of gamma-rays are set as smaller than those of neutrons to maintain the same distribution of the neutron and gamma peaks in the histogram of counts (Sect. 3) as those for other discrimination methods used in this study (i.e., the neutron band on the right side with larger discrimination factors and the gamma-ray band on the left side with smaller discrimination factors).
2.4 Falling edge percentage slope
The falling edge percentage slope (FEPS) method[27, 28] aims to realize fast real-time n-γ discrimination.To realize discrimination using this method, a region of interest (ROI) must be selected, which is located in the region with the most significant differences between n-γ
PSs in the falling edge area.The ROI is specified by setting two thresholds on the top and bottom, termed as Above A threshold (AAT) and Below A threshold (BAT), respectively. The analysis includes finding the intersections between a n-γ PS and these two thresholds:intersection Φ at coordinates (Φx,Φy) for AAT and intersection Ψ(Ψx,Ψy)for BAT.Finally,the discrimination factor,i.e.,the Rs, is calculated as follows:

Usually, the BAT is a constant and set as 10% of the maximum of a n-γ PS, whereas the AAT is a manually determined parameter that varies from 30 to 90% of the maximum. As gamma-ray pulses exhibit a faster decline speed, the absolute value of their Rsis considerably larger than those of neutrons. Additionally, the Rs-values of n-γ PSs are negative; hence, in the histogram of counts of n-γ PSs mentioned in Sect. 3, the gamma-ray band is located on the left side of the neutron band.
2.5 Frequency gradient analysis
The frequency gradient analysis (FGA) method is a frequency-domain-based method with theoretically specialized anti-noise ability as proposed in 2010 [29]. When applying it to n-γ PSs, a radiation pulse signal must be transformed into the frequency domain using the Fourier transform.In contrast to the original time-domain signal,in which the most significant differences between n-γ PSs are located at the falling edge area, the frequency-domain signal exhibits distinct differences between n-γ PSs at the beginning of the signal.The amplitudes of the transformed n-γ frequency-domain signals at zero frequency, equal to the average values of the entire time-domain pulse signals of the neutron and gamma-ray, respectively, significantly differ from each other. Subsequently, two points in the early parts of a frequency-domain signal are selected to calculate the gradient value,Rg,which is further used in the discrimination process. The mathematical formula for the discrimination factor, termed as the frequency gradient, is defined as follows:

where X(f) denotes the frequency-domain signal transformed from an original time-domain n-γ PS using the Fourier transform, f denotes the frequency, which is located at the initial parts of the frequency-domain signal mentioned earlier.The Rg-value of neutrons is greater than that of gamma-rays because of the faster decrease in the frequency domain signals of the neutrons.
2.6 Pulse coupled neural network
A pulse-coupled neural network(PCNN)was introduced into the field of n-γ discrimination by Liu et al. in 2021[19]. It has been shown to exhibit a significantly better performance than almost all the previous discrimination techniques.This is attributed to its ability to recognize and capture the dynamic information in n-γ PSs, which is crucial, if not the most important, information for the discrimination process. This characteristic is inherited from the original structural design and application of the PCNN.Initially,the PCNN was inspired by the biological neuronal cortex of animals. The biological neurons of the visual cortex of animals receive stimulation from their eyes,leading to spike generation and transmission between cell assemblies in the cortex [30, 31]. This interaction between cell assemblies can recognize and analyze the information contained in the stimuli [32] wherein the information is carried by the images that are observed by the eyes of the animals. Due to evolution, this working style of neurons is extremely effective in dealing with dynamic information inside images. Based on these neurological findings, Eckhorn et al. proposed an artificial cortical model [33] that enables computers to obtain parts of the dynamic information processing ability of biological neurons. A few years later,in 1994,Johnson et al.designed a PCNN model based on Eckhorn’s original cortical model for the imageprocessing area [34, 35]. Since then, PCNN has been widely used in many image processing applications such as image shadow removal [36], feature extraction [34], pattern recognition [32], image segmentation [35], and object recognition [37, 38].
The structural design of the PCNN incorporates three closely connected parts: accepted, modulation, and pulse generator domains [39]. First, the link input (LI) and feedback input (FI) constitute the accepted domain, and they are both modulated by the surrounding neurons via weighting matrices M and W.The LI is responsible for the stimulus provided by the surrounding neurons,whereas the input signal’s outer stimulus S mainly affects the FI. Second, the modulation domain controls the relationship between the internal threshold and internal activity by changing the character of the dynamic threshold θ.Finally,the pulse generator domain is responsible for the activation of a neuron by comparing the value of its internal activity U and dynamic threshold θ. If the activity exceeds the threshold, then the neuron is activated (or ignited), and consequently passes a stimulus to its neighboring neurons.The mathematical equations for these activities are as follows [40]:

where F denotes the FI and L denotes the LI; subscripts ij denote the location of a neuron at coordinate (i,j); n denotes the iteration count; αFand αLdenote the decay time constants of FI and LI,respectively;VFand VLdenote the amplification coefficients of FI and LI,respectively;M and W symbolize the weighting matrices of FI and LI,respectively;S denotes the input signal’s outer stimulus;U denotes the internal activity; Y denotes the timing pulse sequence that determines whether a neuron located at (i,j)should be fired (Uij[n ]>θij[n ], Yij[n ]=1) or not fired(Uij[n ]≤θij[n ], Yij[n ]=0); θ denotes the dynamic threshold; β denotes the linking strength, which modulates the contribution from the FI and LI to the internal activity U;αθand Vθdenote the decay time constant and amplification coefficient of the dynamic threshold, respectively.
To discriminate n-γ PSs using the PCNN method [19],the neural network should be first provided with n-γ PSs in order to generate an ignition map(a vector of the same size as the n-γ PS) that corresponds to each fed n-γ PS. The pulse shape differences between neutrons and gamma-rays are amplified and more discernible in the ignition maps of neutrons and gamma-rays. Subsequently, the discrimination factor was obtained by integrating the ignition times(the number of times a neuron at one point is ignited) of parts of the ignition map that correspond to the parts incorporating the falling edge and delayed fluorescence in the original n-γ PS. It should be noted that the discrimination factors of neutrons are greater than those of gammarays because the ignition times of a point are more significant if the amplitude is higher.
3 Evaluation criteria
In this study, Figure of merit (FoM) is used to objectively evaluate the discrimination performance of several methods under different conditions. After the discrimination process, the discrimination results, i.e., the discrimination factors of n-γ PSs,were used to create a histogram.This histogram consists of two bands:the gamma-ray band on the left side and neutron band on the right side.We used a Gaussian fitting function to fit each band and calculated the FoM-value using the following Eq. [41]:

where S denotes the distance between these two bands,FWHMnand FWHMγdenote the full width at half maximum of the gamma-ray (on the left side) and neutron (on the right side) bands, respectively. For an excellent discrimination result, the bands in the histogram are discernibly separated from each other, while each band maintains a Gaussian distribution with low variance. This leads to a larger S-value and smaller FWHMnand FWHMγvalues. This implies that as the FoM value increases the discrimination results become better.
4 Experiment
4.1 Experimental setups and parameter settings
The 9414 n-γ PSs used in the study were collected under excitation from a241Am-Be isotope.To acquire data,we used a TPS2000B oscilloscope (with 200-MHz bandwidth, 1-GS/s sampling rate, and 8 bits of vertical resolution), 9821 B photomultiplier, and n-γ discrimination capable plastic scintillator (EJ299-33). We followed the Shannon criteria [42], the pulse duration was set to 160 ns to prevent the bandwidth from suppressing the information.The trigger threshold was set to 500 mV, which corresponds to a 1.6-MeVee (electron equivalent, i.e., signal produced by 1.6-MeV gamma-ray)threshold.Typical pulse waveforms of neutrons and gamma-rays are shown in Fig. 1.
All parameters of the discrimination methods used in the study are optimized. For the ZC method, τ=1 ns and T =72 ns. For the CC method, we set the range (︿P-10, ︿P+90)ns as the total component,where the ︿P denotes the time when a pulse reaches its maximum value, and the range (︿P+27, ︿P+90) ns denotes the slow component.For the FEPS method, the aforementioned threshold A is set to 60%. For the FGA method, f =1. Finally, for the PCNN method, we set n=180, αF=0∙325, αL=0∙356,αθ=0∙081, VF=0∙0005, VL=0∙0005, Vθ=16∙8,β=0∙67, M =W =[0∙1509,0,0∙1509], and the integration range is set as (︿P-7, ︿P+123) ns.
4.2 Discrimination results and analysis
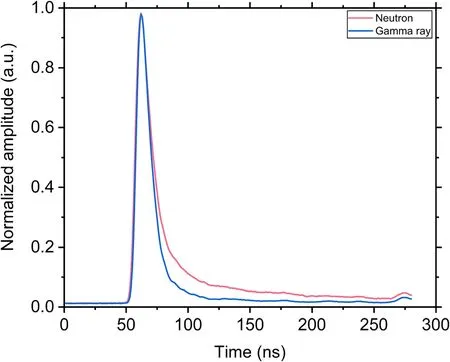
Fig. 1 (Color online) Typical pulse waveforms of neutrons and gamma-rays
Filtering is a standard process for most discrimination approaches, and it reduces the noise from the detection system (e.g., the noise of the photomultiplier tube or random voltage fluctuation). Zuo et al. demonstrated that different discrimination methods include an optimal filtering method, which can exhibit optimal discrimination performance [43]. In the study, the most commonly used filtering method, the Fourier filter, was applied to all discrimination methods to control variables such that the change in FoM is only affected by the type of discrimination method. Additionally, in the study, we focus on the effect of noise. Hence, evaluation was conducted twice as follows:using the raw n-γ PSs and using filtered n-γ PSs.Although ZC, CC, VP, and PCNN methods can work adequately with or without the filter, the FEPS method is unable to correctly discriminate n-γ PSs when the n-γ PSs are not pre-processed by the filter.
Hence, the discrimination processes can be divided into two groups as follows: (i) five methods that benefit from filtering (ZC, CC, VP, FEPS, and PCNN) and (ii) five methods that do not benefit from the filtering process (ZC,CC, VP, FGA, and PCNN). The discrimination results are shown in Figs. 2 and 3 as two-dimensional histograms. In the histograms,count refers to the number of n-γ PSs with a specific range of normalized discrimination factors and normalized maximum pulse amplitudes. The band on the left side originates from gamma-ray pulses, and the band on the right side originates from neutron signals.
As shown in Fig. 2, CC (a) and PCNN (b) methods significantly outperform other methods with band shapes that are consistent with a Gaussian distribution and a wide gap between the gamma-ray and neutron bands. For ZC(c) and VP (d) methods, an excessively high number of n-γ PS counts were located between the bands, and they were difficult to identify. The discrimination performance of the FEPS (e) method is poor given that both bands are smeared (larger FWHM), and thus they almost overlap with each other.
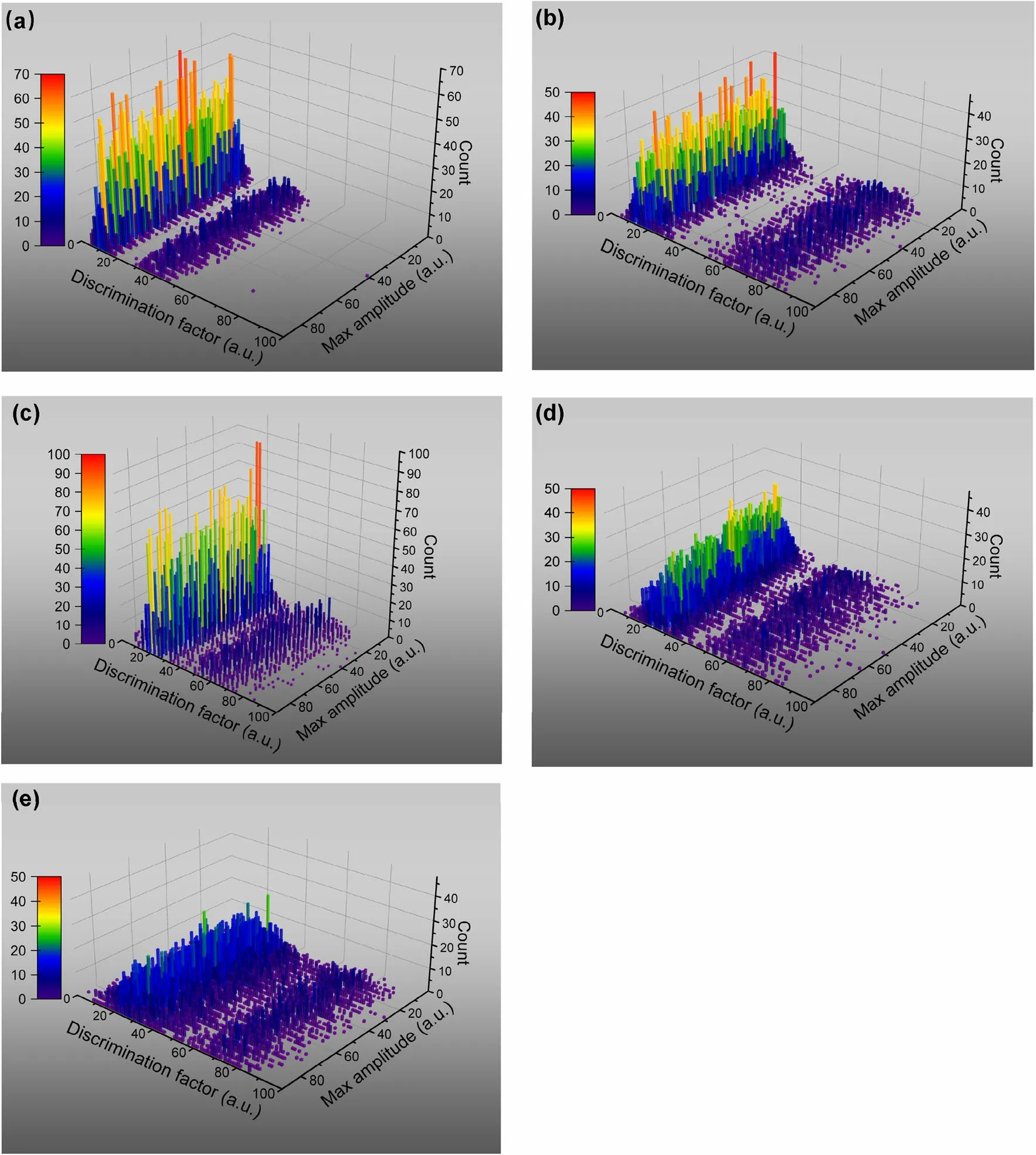
Fig. 2 (Color online) Discrimination results with pre-processed data for the following methods: a Charge Comparison, b Pulse Coupled Neural Network, c Zero Crossing, d Vector Projection, and e Falling Edge Percentage Slope. For the excellent discrimination result, two bands should be separated to leave the minimum possible number of counts between the two bands. Each band should be centrally distributed, thereby maintaining the shape of Gaussian distribution
The results of the raw data processing are shown in Fig. 3. In general, when raw data are used, the discrimination effects of ZC (a) CC (b) VP(c) and PCNN (d)methods are slightly degraded when compared with their performance with filter processing as shown in Fig. 2.The number of counts located between the n-γ bands significantly increased when band widths (FWHM) increased.Evidently, the residual noise in n-γ PS negatively affects the discrimination process. More experiments were performed to determine the specific impact of noise on the different methods,.

Fig. 3 (Color online) Discrimination results using raw data for the following methods: a Zero Crossing, b Charge Comparison, c Vector Projection, d Pulse Coupled Neural Network, and e Frequency Gradient Analysis
Thus, different intensity levels of Gaussian noise were added to the n-γ PSs before the discrimination process to evaluate the different methods.The Gaussian noise X︶follows thedistributionX︶~N (0,0∙2),andtheintensitylevelisdefined as a constant c.The artificial noise added to the n-γ PSs is cX︶.However,it is not possible to represent the effectiveness of a method under a given noise level by the result of a single experiment because different random sequences X︶generated in every independent experiment can lead to different discrimination results. The average discrimination performance tended to be stable only when the number of independent experiments was sufficient.This average performance represents general effectiveness under specific noise conditions.The following steps were performed to determine the effectiveness of the method under a given noise level:
• Independently repeat the discrimination experiment 4000 times.
• A comparison of the averaged FoM-value of the first 2000 times and that of the rest ensures that the difference between them is sufficiently low (less than 0.001).
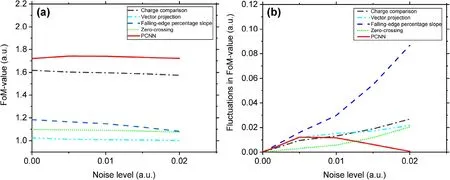
Fig. 4 (Color online) Discrimination performance under noise conditions with filtering process. a FoM-value of different discrimination methods under serval noise levels; b Fluctuations in FoM-value of different discrimination methods under serval noise levels
• The average FoM-value of all 4000 experiments as the discrimination performance under a specific noise level.Hence, we avoided variation in the FoM-value due to random noise, and thus the average performance under a specific circumstance is distinct. The experiment was divided into two groups, similar to the former. First, the n-γ PSs were filtered via the Fourier filter before discrimination, thereby ensuring that the effect of noise mainly originates from the artificially added Gaussian noise with a controllable level.Second, raw n-γ PSs were fed to the discrimination process, and thus the original noise from the radiation detection system remained unchanged and was further artificially increased by Gaussian noise to evaluate the performance of different methods. Their performance was quantified by the FoM-value and its fluctuation,which is defined as the absolute value of the difference between the FoM-value of n-γ PSs without artificially added Gaussian noise and FoM-value under a given level of artificially added noise.For each noise level,the discrimination experiment for each method was performed multiple times (over 4000 times in this study) to obtain an average fluctuation in FoM-value,which denotes the general performance of the method under this specific noise scenario. The experimental results are shown in Figs. 4, 5.
In Fig. 4a, in a manner similar to the intuitive results shown in Fig. 2, the discrimination methods are easily separated into two groups according to their performance.The FoM-values of the PCNN and CC methods fluctuate at approximately 1.7 while those of the other methods are roughly in the range of 1.0 to 1.2 and generally tend to decline as the noise level increases. As shown in Fig. 4b,the FEPS method is the most sensitive to noise, and its fluctuations significantly increase when the noise level increases. This is because the FEPS method relies on the calculation of a certain area’s slope of the falling edge,and this requires n-γ PSs to be highly smooth. They are no longer smooth when Gaussian noise is added to the signals.Hence, the discrimination performance of the FEPS degrades significantly. Given this characteristic, the FEPS method cannot work properly without the filtering process,and it requires a filter to smooth n-γ PSs.The VP,CC,and ZC methods exhibit a similar tendency of fluctuation in the FoM-value, which slowly increases with increases in the noise level. With respect to the PCNN method, its fluctuation initially shares the same pattern with other methods and then surprisingly decreases to zero.This is because the discrimination effect of the PCNN initially improved slightly at the low noise level (as shown in Fig. 4b) and then decreased when the noise level exceeded 0.01. This implies that the PCNN can realize a better discrimination performance under a low-noise scenario than that withoutnoise scenario. This property is realized by tuning the parameters of the PCNN, thereby making it more capable of anti-noise characteristics while sacrificing minimal discrimination performance. The parameter selection strategy is explicitly illustrated in Sect. 4.3.
Figure 5a shows the experimental results without filtering process wherein it is observed that PCNN and CC methods still yield the optimal FoM-value and exhibit stable performance under high noise conditions. However,FGA and VP methods perform poorly under the high noise circumstances wherein the FoM-value fluctuates around 1 and 0.8 values, respectively, which are unacceptable in many n-γ discrimination applications. Additionally, the effect of PCNN does not improve at the low artificial noise level as in the former experiment, thereby suggesting that raw n-γ PSs already contain excessive noise.

Fig.5 (Color online)Discrimination performance under noise conditions without the filtering process.a FoM-value of different discrimination methods under serval noise levels; b Fluctuations in FoM-value of different discrimination methods under serval noise levels
As shown in Fig. 5b, the anti-noise ability of the VP method is unsatisfactory, and its fluctuations increase immediately when artificial noise is added. A comparison of the discrimination performance of the VP method with and without pre-processing indicated that its FoM-values significantly decrease from a normal level to a level that cannot be considered successful. The fluctuations in the FGA method initially increased and then decreased at a higher noise level. Given the frequency domain-based property of the FGA method,it can work well in such high noise condition, with its FoM-value fluctuating at approximately 1.03 and does not show a clear decline tendency.With respect to the CC and ZC methods, their fluctuations in FoM-value were the most stable and remained at a low level under all noise conditions. Finally, for the PCNN method, the change in the fluctuations in FoM-value are almost identical to those of the CC and ZC methods below 0.01 noise level.However,at higher levels,the fluctuations of the PCNN increase faster than those of the CC and ZC methods. The detailed discrimination performances of different methods under different situations are listed in Table 1. The best results of evaluation criteria under each noise condition are marked in bold.
In conclusion, as shown in Table 1, the PCNN method exhibits optimal discrimination performance with and without the filtering process,with FoM-values significantly exceeding those of all other methods. Additionally, the anti-noise ability of the PCNN exceeded that of other methods under filter conditions and reached the same level as the other fluctuation-stabilized methods(such as the CC and ZC methods) when the filtering process was removed.Although the anti-noise performance of ZC and FGA methods is good,their poor discrimination performance is a disadvantage that cannot be ignored. The CC method exhibited a discrimination performance second only to that of the PCNN and even better anti-noise performance under extreme noise conditions. Therefore, for high-noise applications,the PCNN method is recommended because it can remain stable under varying noise conditions and can exhibit an outstanding discrimination performance. However, if the noise conditions are extremely poor, then the use of the CC method is recommended to cross-check discrimination results of the PCNN method for ensuring the accuracy and effectiveness of discrimination results.
4.3 Selection strategy of the parameters of PCNN
The discrimination performance and anti-noise capabilities are closely related to the parameters of the PCNN.Hence, it is important to determine the behavior of the PCNN when these parameters change. In this section, we evaluated the effect of the six main parameters of the PCNN.When a parameter is changed,the other parameters are fixed to the values mentioned in Sect. 4.1. For each parameter, experiments were conducted for different noise levels to determine its effect on anti-noise performance and under a zero artificial noise scenario to estimate its impact on discrimination performance. The experimental results are shown in Fig. 6.In the figure,the Y-axis on the left side denotes fluctuations in the FoM value measured for different noise levels, and the Y-axis on the right side represents the FoM value measured without artificial noise.
As shown in Fig. 6a, the FoM-value declines from approximately 1.85 to 1.65, with some periodical fluctuation when the value of αFincreases while the fluctuations in FoM-value stabilize at their lowest level when the value of αFis approximately 0.325. The αFis responsible for the decay rate of the FI. A larger αFvalue indicates a faster return of activated neurons to the resting state. Hence, it increases the ignition frequency of the neuron. If the αFvalue is excessively low, then the ignition frequency of each neuron in the PCNN decreases, thereby adversely affecting the information recognition ability of the PCNN.Conversely, if the αF-value is excessively high, it suppresses the effect on a neuron from its former iteration,and thus the FI is heavily reliant on the outer stimulus, which can deteriorate the discrimination and anti-noiseperformance of the PCNN.Hence,αFshould be selected as approximately 0.325. As shown in Fig. 6b, a change in αLdoes not affect the discrimination or anti-noise capabilities over a wide range.This is because αLis responsible for the behavior of the LI, whereas the LI is not extremely important in n-γ discrimination applications. The discrimination process mainly depends on the FI to extract information from n-γ PSs, whereas the LI only slightly moderates the internal activity of neurons.Any value from 0.34 to 0.36 is acceptable for αL.

Table 1 Discrimination performance under various noise conditions
As shown in Fig. 6c, the FoM-value fluctuated at approximately 1.7 when the M changes without an obvious pattern whereas the fluctuations in FoM-value tended to decrease when the value of M increased.The M affects the contribution of the surrounding neurons to the central neuron. Increases in the value make the connection between neighboring neurons closer.A stronger connection between neurons decreased the sensitivity of PCNN to the random fluctuation of the pulse signals,i.e.,it improved in terms of ignoring extraneous noise and focusing on the information carried by the signals. The recommended range of M-value was 0.15 0.28. As shown in Fig. 6d, the performance of the PCNN was steady for β values of β lower than 0.72. For values exceeding this value, the performance of discrimination and noise immunity significantly decreased. This degradation originated from the relationship imbalance between FI and LI. As previously mentioned, FI is more important in n-γ discrimination applications. When the β value increased, the contribution of LI to the internal activity also increased, which directly decreased the contribution of FI’s because the internal activity consisted of FI and LI.Thus,if the contribution of one increases, that of the other must proportionally decrease. Therefore, the β values should be lower than 0.65.
Figure 6e and f shows the effect of the two parameters related to the dynamic threshold. The αθ, which is responsible for the decay speed of the dynamic threshold,exhibited an apparent optimal value range of approximately 0.083–0.088.In this range,discrimination and antinoise capabilities were good. With respect to the amplification coefficient Vθ,the FoM-value decreased from 1.9 to 1.5 when Vθincreased. The fluctuations in FoM-value initially ameliorated when the value of Vθincreased from 15 to 17. However, the fluctuations significantly increased when Vθexceeded 17. The Vθaffects the amplification speed of the dynamic threshold.A larger Vθ-value leads to a faster amplification speed, thereby curtailing the ignition process of the neurons and decreasing the ignition frequency.This negatively impacts the information extraction ability of the PCNN and results in a decrease in the FoMvalue as shown in Fig. 6f. Meanwhile, the considerable amplification speed makes it difficult for the dynamic threshold to be exceed by the stimulus of noise, which explains increases in the PCNN’s noise immunity in the middle range of Vθvalue.The value of Vθshould be in the 16–16.5 range.
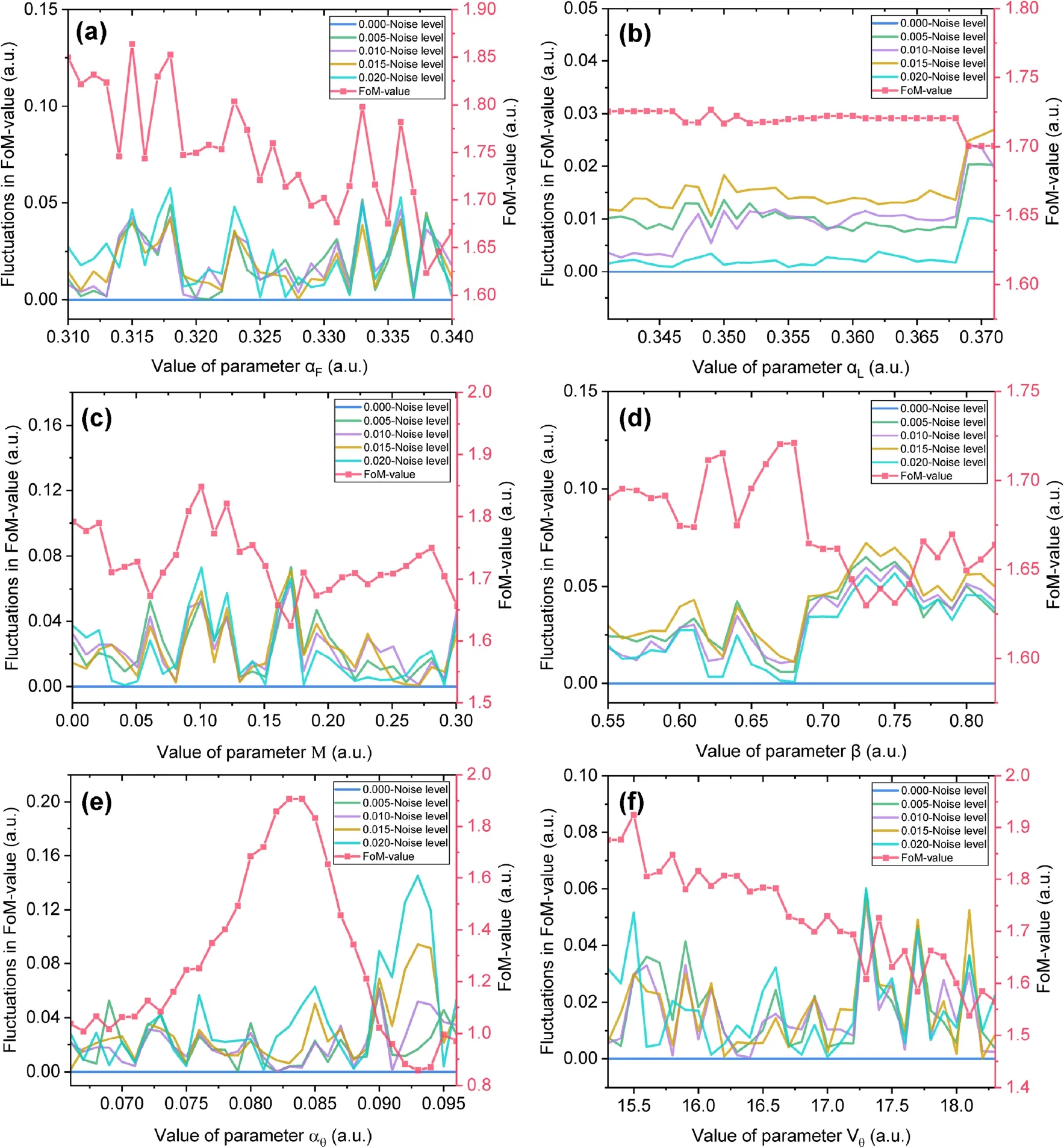
Fig. 6 (Color online) Effects of different parameters on the FoMvalue and fluctuations in FoM-value under serval noise conditions.a Decay time constant of feedback input αF;b Decay time constant of link input αL;c Weighting matrixes M;d Linking strength β;e Decay time constant αθ;f Amplification coefficient Vθ.The Y-axis on the left side denotes the fluctuations in FoM-value, measured for different noise levels; and the Y-axis on the right side represents the FoMvalue, which is measured without artificial noise
In general, all parameters of the PCNN can be selected from a wide range and still achieve an acceptable discrimination performance (with FoM-value from 1.6 to 1.9) and anti-noise performance (with fluctuations in FoM-value under 0.04). The result indicates that the PCNN method is not heavily constrained by its parameters when applied to n-γ discrimination. In addition, the effect of many parameters on discrimination and anti-noise performance steadily fluctuated when the values of the parameters were within a reasonable range whereas the performance significantly decreased when the values were selected at extremes.The reason for this phenomenon was that the PCNN was composed of several closely connected parts. Hence, when the parameter responsible for one part exhibited significant changes, the other parts modulated it to make it work accurately. For example, if the αFwas excessively low, the decay speed of the FI significantly decreased, and the FI increased accordingly and provided a stronger stimulus to the internal activity.Nevertheless,the internal activity did not make the neurons stay activated forever. The dynamic threshold was amplified more times than in the usual αF-value scenario such that the neurons returned to the initial state. However, the modulation ability exhibited certain limitations. Modulation failed if the selected parameter was excessively radical to maintain the connection between different parts of the PCNN, thereby decreasing the performance of the PCNN.
5 Conclusion
In the study, the anti-noise performance of the PCNN method for n-γ discrimination was evaluated. The n-γ pulses used in the study were generated via a plastic scintillator(EJ299-33)under241Am-Be excitation.A 9821 B photomultiplier and an oscilloscope with 200-MHz bandwidth, 1-GS/s sampling rate, and 8-bit vertical resolution were used to collect data. It is noted that the sampling rate of the oscilloscope influences the discrimination performance. The experiments were divided into two runs as follows:in the first run,pulses were pre-processed using the Fourier filter to reduce original noise in the signals,and in the second run, original raw signals were used to simulate an extremely high-noise scenario. For each run,artificial Gaussian noise at different levels was added to the signals before the discrimination process. Under these circumstances, the performance of the PCNN was evaluated and quantified via FoM-values and their fluctuations.The performance of the PCNN was compared with the other five commonly used methods, namely zero crossing,charge comparison, vector projection, falling edge percentage slope, and frequency gradient analysis.
The experimental results indicated that the PCNN method outperforms most other methods(CC is close)in FoM-value under all noise conditions. Furthermore, the fluctuations in FoM-values were lower for the PCNN than for the other methods when the pulse signals are pre-filtered under most conditions. Only for the additional artificial noise at high levels, the fluctuations in the FoM-values of the PCNN exceeded those of the CC and ZC methods. The results demonstrated that the PCNN method exhibits outstanding anti-noise capability and can be applied to high-noise applications. Additionally, experiments were conducted to evaluate the effect of PCNN parameters.Variations in FoMvalues and their fluctuations were observed under different noise conditions. The experimental results suggested that PCNN does not rely on strict parameter settings and can realize satisfactory performance over a wide parameter range.In conclusion,the PCNN method is suitable for use in high-noise scenarios due to its stability and excellent discrimination performance.A future study will further validate the feasibility of the PCNN in processing pulse signals recorded for different scintillator materials.
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing,adaptation,distribution and reproduction in any medium or format,as long as you give appropriate credit to the original author(s) and the source,provide a link to the Creative Commons licence,and indicate if changes were made.The images or other third party material in this article are included in the article’s Creative Commons licence,unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Author contributions All authors contributed to the study conception and design. Material preparation, data collection and analysis were performed by Hao-Ran Liu, Zhuo Zuo and Peng Li. The first draft of the manuscript was written by Hao-Ran Liu and all authors commented on previous versions of the manuscript. All authors read and approved the final manuscript.
 Nuclear Science and Techniques2022年6期
Nuclear Science and Techniques2022年6期
- Nuclear Science and Techniques的其它文章
- The role of deformations and orientations in an alpha ternary fission of Thorium
- Feedforward compensation of the insertion devices effects in the SSRF storage ring
- A new radar stealth design excited by 210Po and 242Cm
- Development of an ultrafast detector and demonstration of its oscillographic application
- Low-radioactivity ultrasonic hydrophone used in positioning system for Jiangmen Underground Neutrino Observatory
- Study on analytical noise propagation in convolutional neural network methods used in computed tomography imaging
