盘式制动器制动片数量对其温度场及应力场的影响分析
*刘 洋
(神华准格尔能源有限责任公司物资供应中心 内蒙古 010300)
引言
盘式制动器与传统的钳盘式制动器相比,制动器使用寿命长、制动性能稳定、耐磨损、散热效果好、摩擦副温度降低显著,可通过改变弹簧的模量和数量来获得不同制动力矩,也可通过改变摩擦盘数量,获得不同大小的制动力矩,而不增大径向尺寸。可实现间隙自动调整,维修方便[1]。现已大量运用在电铲、自卸卡车等大型采矿设备中,还可应用于架桥机、水库提升机、起重机等重型机械设备中。大型矿用机械为了保证作业过程的安全,多采用盘式制动器作为构成制动系统的关键部件,因此在大型电铲中,盘式制动器俗称抱闸,是一种失电安全制动器,出现故障容易导致卡车溜车、电铲掉铲斗以及溜铲事故,轻则造成设备财产巨大损失,重则对人身安全造成巨大危害。但矿用机械具有功率大、载荷大的特点,且工作环境较为恶劣,对盘式制动器的性能提出了很高的要求。在工作制动及紧急安全制动情况下,制动器产生大量的摩擦热,摩擦副中制动片与对偶件接触区域非理想的压力场分布会影响摩擦热的生成,形成非均匀分布的温度场,导致接触区域热应力不一致,进而引起热应变的差异,反过来影响接触区域的压力场分布,盘式制动器的制动过程是典型的高度非线性的热-结构耦合的物理过程[2-3]。制动过程中,温度过高会引发“制动效能热衰退”“制动器疲劳破坏”等一系列问题[4]。
1.国内研究现状
针对制动器热-结构耦合问题,已有部分学者进行相关研究:制动过程中摩擦生热会产生不均匀温度场,制动盘在受热情况下产生热弹性变形,从而改变了接触状态和接触压力的变化,从理想接触状态转变成不均匀接触,明显影响制动器振动、噪声特性,同时加速了摩擦磨损[5-6]。黄健萌等[7]针对钳盘式制动器存在移动式热源的情况,通过建立温度/应力场同一的仿真模型,发现二者存在着耦合关系,并具有周期性变化规律,这是由于移动热源产生的热冲击和表面对流换热引起的,并指出热冲击是引起制动盘出现热疲劳裂纹,接触表面摩擦特性发生改变的重要因素。张立军[8]在考虑活塞侧和钳指侧制动块法向力不同作用方式下,建立三维瞬态热机耦合动力学有限单元模型,其分析指出摩擦力导致载荷转移效应的发生,活塞侧与钳指侧的接触压力受到结构、法向力和制动盘翘曲变形的综合影响而截然不同。陆超[9]利用ABAQUS非线性多物理场耦合方法进行制动器热—结构分析,利用数值模拟了列车制动过程,同样得到在摩擦副上温度与接触应力表现不均匀分布的规律。黄晓华[10]利用ABAQUS进行动车制动器的热-结构分析,采用Goodman-Smith疲劳极限图对制动盘的疲劳强度进行验证,将分析获得的的温度-应力载荷谱通过Fe-safe软件开展热疲劳寿命预测分析研究,通过寿命预测可以制定适应的维护保养计划,从而避免部分故障、事故的发生,具有较大的应用价值。李建峰[11]采用热-结构耦合分析方法,从多个参数从发,探索提升机盘式制动器的优化方法,以改善盘式制动器的热应力分布状态,减小制动盘最高温度,延长盘式制动器的使用 寿命。
综上所述,制动器热-结构耦合具有重要意义,本文从工程实践的角度出发,利用ABAQUS建立摩擦副的热-结构耦合有限元模型,对制动过程进行仿真模拟,以制动片的数目为变量,探究其对制动器温度及应力的影响,为制动器的设计与优化提供依据,具有较强的现实意义。
2.盘式制动器简介
(1)盘式制动器的作用
本文所研究的盘式制动器位于电铲车的提升机构、回转机构、推压机构以及行走机构中,通常与电机配合完成机构制动,即提升机构、回转机构、推压机构以及行走机构先由电机进行制动,电机将运动机构制动到较低速度时,再由盘式制动器进行制动并长期保持,这一情况下盘式制动器被视为“静态”制动器。但在特殊情况下,如偶然的电气失效,电机将失去对各机构的控制能力,此时盘式制动器必须能够将运动机构停住并保持,在这种工况下,盘式制动器将面临巨大热负荷的考验。这一工况对电铲车的安全使用存在巨大挑战,因此本文亦使用该工况条件进行研究。
(2)盘式制动器的工作原理
本文分析的是一种弹簧上闸、气压释放的常闭式盘式制动器,其基本零件包括花键轴、壳体、由制动片及基体铆接形成的制动盘、对偶件、压盘、气缸、活塞及压缩弹簧等。花键轴通过平键及锥面与负载轴连接,制动盘由花键轴支承,非制动状态下可随花键轴与负载轴一起转动,对偶件周向始终与壳体保持静止。制动时,在压缩弹簧预压力作用下,压盘推动制动盘及对偶件沿轴向内移,相互压紧,由各接触面的摩擦产生制动力矩;释放时,气缸充气带动活塞及压盘外移,在分离弹簧力作用下,制动盘等相互分离,各摩擦面间保持约1mm的间隙,制动盘的旋转自由度被释放。
该制动器的结构如图1所示。
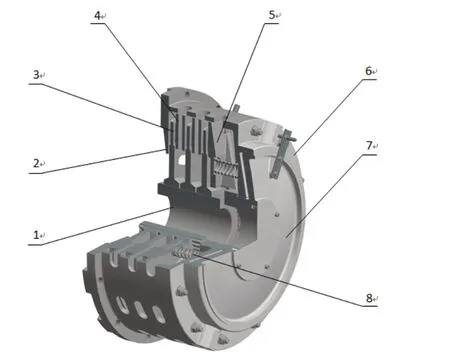
图1 盘式制动器结构图
(3)盘式制动器的特点
盘式制动器选用热膨胀系数小、比重较轻、强度高、抗冲击性能好的材料,其中摩擦副材料还需满足摩擦系数高、耐高温、耐磨性好的要求。该型盘式制动器具有结构紧凑,制动力矩大的特点,安全性能好的特点。
3.热-结构耦合模型的建立
本文采用直接耦合法建立盘式制动器的热-结构耦合模型,通过将温度和机械边界条件赋予模型,直接求解制动器的温度场和应力场分布[2,10]。本文不考虑材料磨损及热辐射的影响,同时假定摩擦消耗的能量全部转化为摩擦热,摩擦副材料均各向同性[9-10,12]。
制动过程中,热载荷以热流密度的形式施加于摩擦表面,并被制动片和对偶件吸收。热流密度满足q(x,y,t)=μp(x,y,t)v(x,y,t),式中,p(x,y,t)为摩擦表面上的比压,μ为摩擦系数,v(x,y,t)为制动片及对偶件间的相对移动速度。制动片和对偶件间的热流分配系数满足,式中,k1、c1、ρ1和k2、c2、ρ2分别为制动片和对偶件材料的热传导系数、比热和密度[2-4,10,12-14]。
制动过程中,存在与周边空气以热对流形式的热耗散,对流换热系数由决定流体特征的雷诺数Re确定,对流换热系数满足,式中,k3为空气热传导系数;D为对偶件外直径[2-4,10,12-14]。
4.有限元仿真模型的建立
(1)ABAQUS简介
ABAQUS是一套功能强大的工程模拟的有限元软件,有两个主求解器模块-ABAQUS/Standard和ABAQUS/Explicit。ABAQUS/Standard适合求解静态和低速动力学问题,这些问题通常都对应力精度有很高的要求,例如垫片密封问题、轮胎稳态滚动问题或复合材料机翼裂纹扩展问题。ABAQUS/Explicit是特别适合于模拟瞬态动力学为主的问题的有限元产品,ABAQUS/Explicit能够高效地求解包括接触在内的非线性问题和许多准静态问题。其解决问题的范围从相对简单的线性分析到许多复杂的非线性问题。ABAQUS热-结构耦合分析具有以下特性:稳态响应、瞬态响应,可采用自适应时间步长、完善的热传导边界条件、材料非线性、热“接触”允许接触面热流动、强制热对流,因此本文选择ABAQUS/Explicit显示分析方法进行热-结构耦合的瞬态响应分析,并定义了与空气的强制热对流。
(2)制动器几何模型的创建
从图1可以看出本文研究的盘式制动器由多对摩擦副组成,考虑到每对摩擦副的工况相同,若建立完整模型可能出现接触关系过多,计算量过大,导致计算成本过大,因此进行简化,取其中一对进行研究。此外还可以看出模型中还有大量花键特征、孔特征及铆接特征,这些特征将给网格划分带来困扰,导致网格质量较低,严重时可能会导致计算过程因无法收敛而停止,而这些特征在时间较短的瞬态分析中,对热传导的影响极小,因此本文对模型特征做一定简化,确保仿真模型的有效性。
为研究制动片数目的影响,本文在摩擦面比压、总摩擦面积一定的情况下,以制动片数目N作为变量,研究其对制动器温度场和应力场分布情况的影响。选取摩擦副作为对象,去除摩擦副中对结果影响较小的特征,在Inventor中建立制动片、对偶件几何模型(如图2所示),制动片内、外半径分别为240mm、317.5mm,对偶件内、外半径分别为240mm、362.5mm,以.igs格式导入ABAQUS,完成摩擦副的装配。本文共有3种摩擦副模型,制动片数目N分别为6、12、18,制动片、对偶件及摩擦副模型分别如图3所示。

图2 制动片与对偶件简化模型


图3 摩擦副简化模型
(3)定义材料属性及参数
摩擦副中,制动片材料为粉末冶金,密度为5500kg/m3,泊松比为0.3;对偶件材料为HT250,密度7220kg/m3,泊松比为0.3。制动片和对偶件材料的其它性能参数如表1、表2所示[3]。

表1 制动片材料性能参数

表2 对偶件材料性能参数
(4)划分网格
网格划分是ABAQUS热—结构耦合分析的关键,对计算精度和计算成本具有重要影响,ABAQUS网格划分的要点主要在与网格质量、网格密度、网格类型。若网格划分质量过差,可能导致结果与实际误差过大而失去意义,严重可能会导致计算过程因无法收敛而停止,无法进行计算。网格密度过大可能导致无法准确模拟物理参数分布情况,结果精度不高,而网格密度过大,会造成计算量急剧增加,显著增加计算成本,可能出现计算过程长达数月,不为工程实践所接受,且与计算精度增加却不成正比,收获与付出不匹配,因此网格密度的选择一定要合理,此外网格类型也要根据研究问题和计算方法合理选择,否则可能导致计算结果失真。
本文根据以往仿真经验和大量尝试,最终确定摩擦副模型的合理划分方式,选取同时具有结构与温度自由度的C3D8T单元类型,接触区域增大网格密度,其余部分减小网格密度,兼顾计算精度与计算效率。以N=18时的摩擦副模型为例,最终网格划分结果如图4所示。

图4 摩擦副有限元网格
(5)赋予分析边界条件
本文模型中设置两个动力、温度-位移、显式分析步,第一个分析步模拟制动片与对偶件表面接触,压力由0增至恒定制动压力的过程,步长时间较短;第二个分析步模拟制动盘由初始角速度110rad/s匀减速制动至静止的过程,步长时间较长。整个过程中,制动压力以压强形式均匀施加在对偶件非接触面上,对偶件仅保留轴向的平移自由度,制动片在第一个分析步中被约束全部自由度,在第二个分析步中取消对其周向旋转自由度的约束,通过与制动片耦合的参考点控制制动片的旋转,制动初始角速度及幅值曲线施加在参考点上。定义接触时,设定对偶件表面为主面,制动片表面为从面,热流在接触面上生成并分配给接触部件。同时,设置摩擦副与环境的热对流换热,取环境温度为20℃。本文三个模型的边界条件设置完全一致。
5.温度场及应力场仿真结果分析
对应N=6、12、18的模型,各自制动片上的温度分布情况如图5所示。各模型中制动片上温度分布情况相似,制动片内部区域温度高,四周边缘部位温度低,制动过程中最高温度分别为194.5℃、201.9℃、203.1℃,出现在制动片径向靠近外侧的位置。
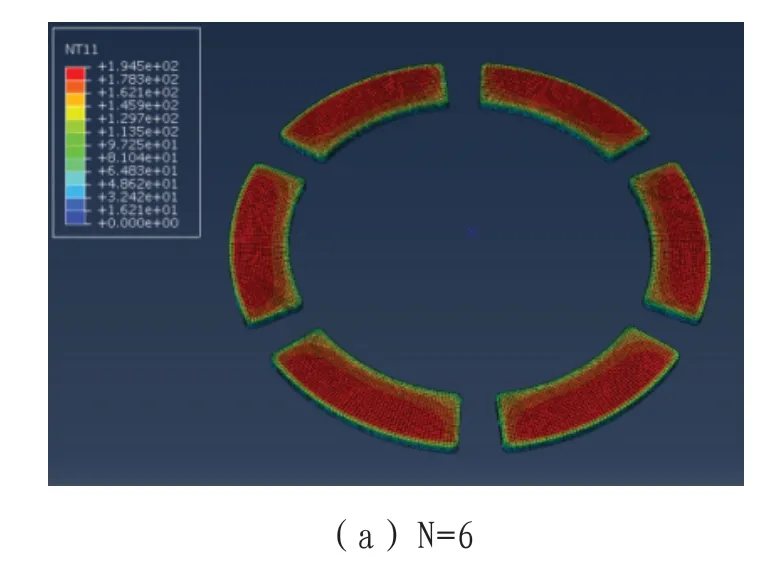
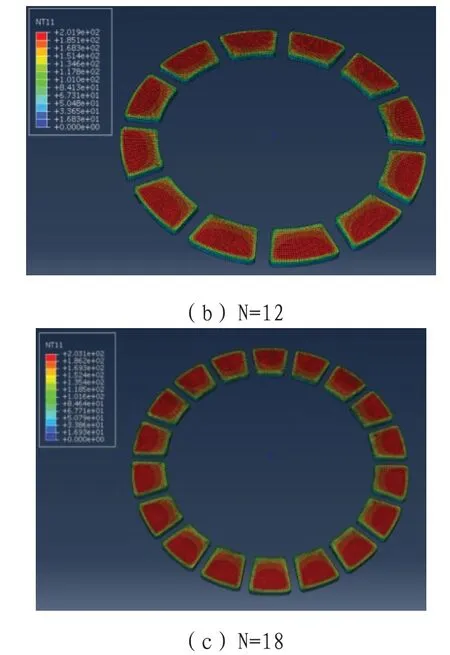
图5 制动片温度分布图
对应N=6、12、18的模型,各自制动片上的应力分布情况如图6所示。各模型中制动片上应力分布情况相似,在靠近制动片外侧的部位出现应力低值,制动过程中最大应力值分别为1.52MPa、1.637MPa、1.711MPa。
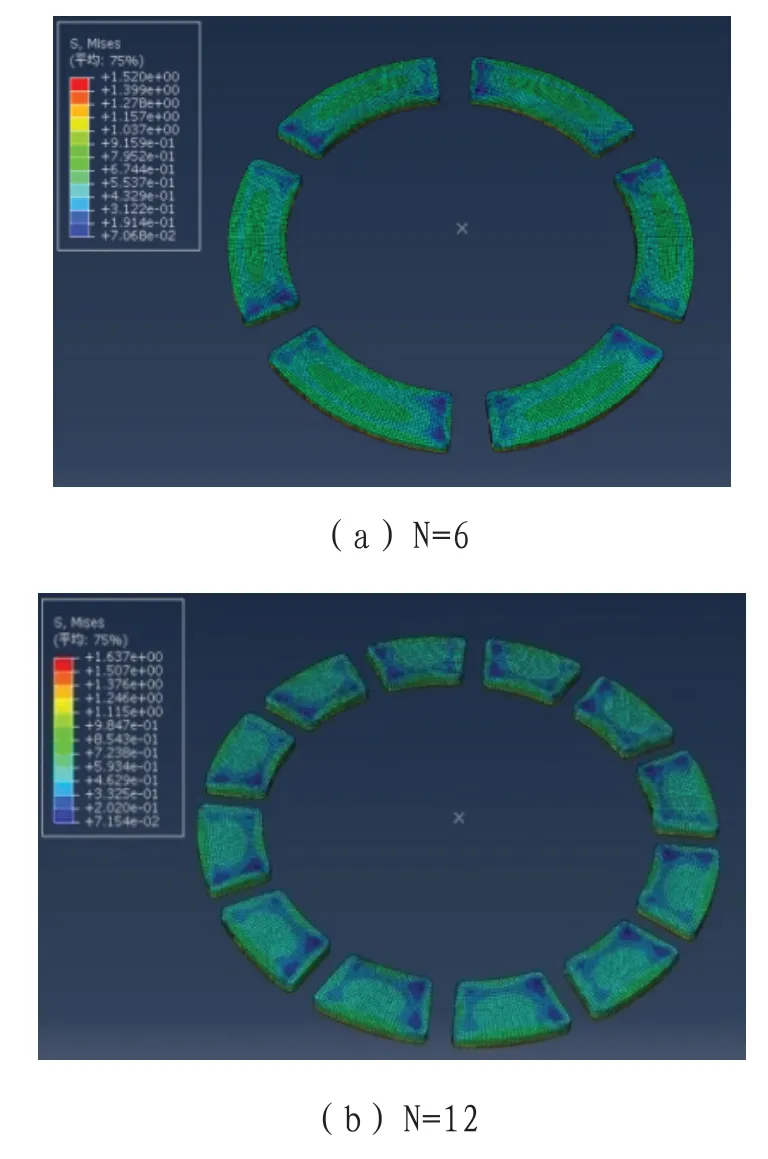
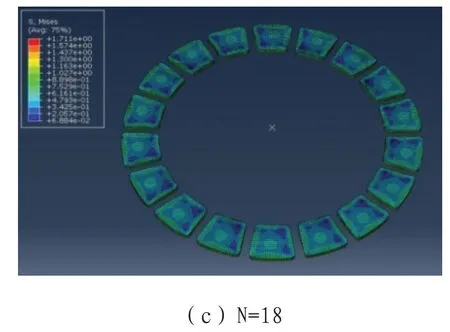
图6 制动片应力分布图
理论上,越靠近外侧,相对滑移速率越大,发热量越多,同时外侧受对流换热影响较大,故制动片上内部区域温度应较高,最高温度应出现在径向靠外侧的位置,四周边缘部位温度相对较低,对应温度低的部位出现应力低值,仿真结果中温度、应力的分布情况与理论一致。
6.结束语
通过仿真结果对比分析可知,负载一定时,在总摩擦面积不变的条件下,改变制动片的数目对制动过程中温度和应力分布影响较小,可忽略不计;设计时可从制动片加工、装配难易程度等经济性角度进行考虑,合理选取制动片数目。

