C语言函数的递归调用
秦玉平,冷强奎,马靖善
(1.渤海大学 数学科学学院,辽宁 锦州121013;2.辽宁工程技术大学 电子与信息工程学院,辽宁 葫芦岛125105;3.渤海大学 信息科学与技术学院,辽宁 锦州121013)
0 引言
递归是一种重要且应用广泛的程序设计方法[1-4].使用递归既便于程序的编写和调试,又能使程序结构简洁清晰、可读性好[5].
在C语言中,函数是构成C程序的基本单位,函数可以递归调用,即在一个函数的函数体中可以直接或间接地调用该函数本身,这个函数称为递归函数.
函数是C语言的重点,递归函数又是学习函数的难点.为便于学习者深入理解C语言中函数递归调用的运行机制,并熟练使用递归调用进行C语言程序设计,本文对C语言递归函数的定义、递归条件、递归函数设计、递归调用执行过程以及递归转换成非递归的方法都进行了详细阐述,并通过实例进行了深入解析.
1 递归函数定义
根据调用方式,递归调用分为直接递归和间接递归两种.
直接递归函数定义的一般形式为:
[存储类别][返回值类型]函数名(形式参数表)
{
┇
函数名(实际参数表);
┇
}
间接递归函数定义的一般形式为:
[存储类别1][返回值类型1]函数名1(形式参数表1)
{
┇
函数名2(实际参数表2);
┇
}
[存储类别2][返回值类型2]函数名2(形式参数表2)
{
┇
函数名1(实际参数表1);
┇
}
【例1】用直接递归计算n!.
long F(int n)
{long s;
if(n==0||n==1)s=1;
else s=n*F(n-1); /*直接递归调用*/
return s;
}
【例2】用间接递归计算n!.
long F(int n)
{if(n==0||n==1)return 1;
else return n*G(n-1); /*函数F调用函数G*/
}
long G(int n)
{return F(n);} /*函数G调用函数F*/
2 递归调用条件
一般地,一个能用递归函数解决的问题须满足两个条件:一是该问题能够缩小规模且缩小规模后的问题与原问题具有相同的求解方法,即能够归纳出递归项,又称递归体;二是须有递归结束的条件,又称递归出口.具体而言,一个递归模型由递归项和递归结束条件两部分组成.
递归结束条件确定递归到何时结束,其一般格式为:
F(S0)=C0
(1)
其中,S0和C0都是常量,C0表示问题规模为S0时的解,一些递归问题可能有多个递归出口.
递归项确定递归方式,其一般格式为:
F(S)=G(F(S1),F(S2),…,F(Sm),C1,C2,…,Cn)
(2)
其中,S是原问题,S1、S2、……、Sm是与原问题解法相同的小问题,C1、C2、……、Cn表示能用非递归方法解决的问题.G是一个函数,表示递归问题的结构.
例如,例1的数学模型为:
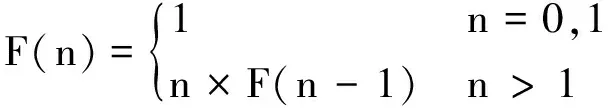
(3)
递归项为F(n)=n × F(n-1),递归结束条件为F(0)=1和F(1)=1.
如果要解决的问题不是计算求值,而是完成指定的操作(如输出等),则其递归模型难以用数学表达式描述,此时可以用解决问题的操作步骤描述.
3 递归函数设计
用递归形式的函数解决实际问题时,首先要给出递归模型,即给出递归项和递归结束条件,然后用C语言函数描述递归模型.其中的关键是递归模型设计,具体步骤如下:
(1)对原问题F(S)进行分析,将其分解为小问题F(S1)、F(S2)、……、F(Sm),并保证每个小问题的求解过程和环境都与原问题相似;
(2)假设每个小问题F(Si)(i=1,2,…,m)都是可解的,在此基础上确定F(S)的解,即给出F(S)与F(S1)、F(S2)、……、F(Sm)之间的关系;
(3)确定特定情况的解,以此作为递归结束条件.
【例3】用递归法计算Fibonacci序列第n项的值.
Fibonacci序列第1项和第2项的值都是1,从第3项起每项的值是其前两项的和.设第n项的值为F(n),则将原问题F(n)分解为F(n-1)和F(n-2),且F(n)与F(n-1)和F(n-2)的关系为F(n)=F(n-1)+F(n-2),特定情况的解为F(1)=1和F(2)=1.由此可知,该问题的数学模型为:
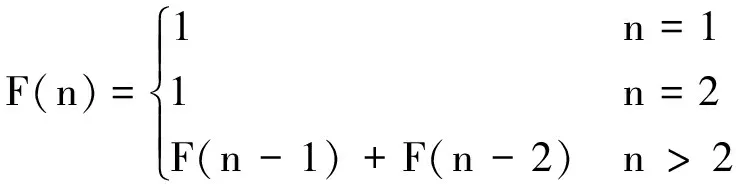
(4)
递归模型式(3)的C语言函数描述如下.
long Fib(int n)
{long f;
if(n==1||n==2) f=1; /*递归出口*/
else f=Fib(n-1)+Fib(n-2); /*递归项*/
return f; /*返回结果*/
}
【例4】先序递归遍历二叉树.
先序递归遍历二叉树的操作步骤如下.
若二叉树为空,则遍历结束,否则进行下列操作:
(1)访问(输出)根结点;
(2)先序递归遍历根的左子树;
(3)先序递归遍历根的右子树.
递归项为(1)~(3)三步,递归结束条件是二叉树为空(NULL).
上述操作步骤对应的C语言函数描述如下.
typedef char ElemType; /*结点数据域类型,假设为字符型*/
typedef struct node
{ElemType data; /*数据域*/
struct node*lchild,*rchild; /*左右指针域*/
}BitTree; /*结点类型*/
void PreOrder(BitTree*bt)
{if(bt!=NULL)
{printf("%c",bt->data);
PreOrder(bt->lchild); /*递归调用*/
PreOrder(bt->rchild); /*递归调用*/
}
}
4 递归调用执行过程
递归调用实质上是嵌套调用的一种特殊情况,所不同的是递归调用的调用函数和被调用函数是同一个函数,每执行一次调用就向递归结束条件靠近一步,当遇到递归结束条件时再逐层返回.递归函数的执行次数称为递归的层数,又称递归深度.第一次调用是由主调函数进入第一层,第i(1 图1 递归调用过程 由图1可以看出,递归调用的求解过程包括下推和回代两个阶段.下推阶段是从原问题出发,逐渐缩小问题的规模,直到递归结束条件,最终实现从未知到已知.回代阶段是从已知出发,按照下推的逆过程逐一求解,最终到达下推的开始处,完成对原问题求解.例如,用例1求4!的递归调用求解过程如图2所示. 图2 递归调用求解过程 在C语言中,函数调用开始,为自动型局部变量分配存储单元,函数调用结束释放[6-7],并返回到调用函数的固定位置继续执行后面的语句.因此,在递归调用的下推阶段需要保存自动型局部变量值和返回地址等现场信息,在回代阶段需要恢复现场信息,这些现场信息的管理是通过系统工作栈来实现的.在递归函数开始运行时,系统先为递归函数建立一个系统工作栈.在每次递归调用开始前,系统自动将当前层的自动型局部变量值和返回地址等现场信息压栈;在每次递归调用结束后,又自动弹栈,把栈顶元素值分别赋给上一层相应的局部变量,使它们都恢复到调用前的状态,并将程序控制转到返回地址指定的位置. 递归问题都可以转换成非递归问题[8-10].依据递归调用在函数中的位置,递归调用分为尾递归调用和非尾递归调用.这两种递归在转换成非递归时使用的方法不同.尾递归调用是指递归调用在函数的尾部,后面没有要执行的语句,其求解过程不进行回溯,转换成非递归时使用工作变量保存现场信息,称为中间变量法.非尾递归调用是指递归调用的后面还有要执行的语句,其求解过程要进行回溯,转换成非递归问题时使用工作栈保存现场信息,称为工作栈法. (1)中间变量法 转换方法是先设置用于保存现场信息的变量,然后从递归出口开始,根据递归项依次求解规模较大的子问题,直至得到原问题的解.其一般过程如下: 设置变量 while(没到原问题规模) {求解当前规模问题 扩大问题规模 } 一般地,为函数的每一个形参设置一个局部变量.另外,根据求解关系设置一些存放中间结果的变量. 【例5】将例3转换成非递归. long Fib(int n) {long i=3; /*设置形参对应的变量*/ int f1=1,f2=1,temp; /*设置存放之间结果的变量*/ while(i<=n) /*循环终止条件为i>n*/ {temp=f1+f2;f1=f2;f2=temp; /*求解子问题*/ i++; /*修改形参对应变量值*/ } return f2; } (2)工作栈法 转换方法是先设置用于保存现场信息的工作栈,然后用循环模拟递归求解过程.其一般过程如下: 设置栈并初始化 原问题现场信息压栈 while(栈非空) {弹栈 处理有解子问题 未求解子问题现场信息压栈 } 一般地,用一维数组表示顺序栈,其类型与相应的函数参数类型相同,栈长不小于递归的深度. 【例6】将例4转换成非递归. #define MAXSIZE 20 /*设置栈长,假设为20*/ void PreOrder(BitTree*bt) {BitTree*stack[MAXSIZE],*p=bt; /*设置栈和形参对应的变量*/ int top=0; /*栈初始化*/ if(bt!=NULL) {stack[top++]=p; /*根结点指针压栈*/ while(top>0) {p=stack[--top]; /*弹栈*/ printf("%4c",p->data); /*遍历(输出)*/ if(p->rchild) stack[top++]=p->rchild; /*右子树根结点指针压栈*/ if(p->lchild) stack[top++]=p->lchild; /*左子树根结点指针压栈*/ } } } 在将递归转换成非递归时,可同时使用栈和变量保存现场信息.例如,将例4转换成非递归时可用下面方法.此时用变量p保存左子树根结点信息,用栈stack保存右子树根结点信息. void PreOrder1(BitTree*bt) {BitTree*stack[MAXSIZE],*p=bt; /*设置栈和形参对应的变量*/ int top=0; /*栈初始化*/ stack[top++]=p; /*根结点指针压栈*/ while(top>0) {p=stack[--top]; /*弹栈*/ while(p) {printf("%4c",p->data); /*遍历(输出)*/ if(p->rchild) stack[top++]=p->rchild; /*右子树根结点指针压栈*/ p=p->lchild; /*用变量保存左子树根结点指针*/ } } } 用C语言求解具有递归特征的问题时,可采用递归函数来实现.递归函数设计的步骤是先找到求解问题的递归项和递归结束条件,然后用C语言函数描述.递归调用具程序结构清晰、代码量少、可读性好等优点.但它也有执行效率低、占用内存空间多等缺点.其原因是递归调用需要栈空间保存现场信息,递归的层次越多,需要的存储空间越多,压栈和弹栈的时间开销也越多.因此,在对执行效率要求较高的情况下,需将其转换成非递归方式.
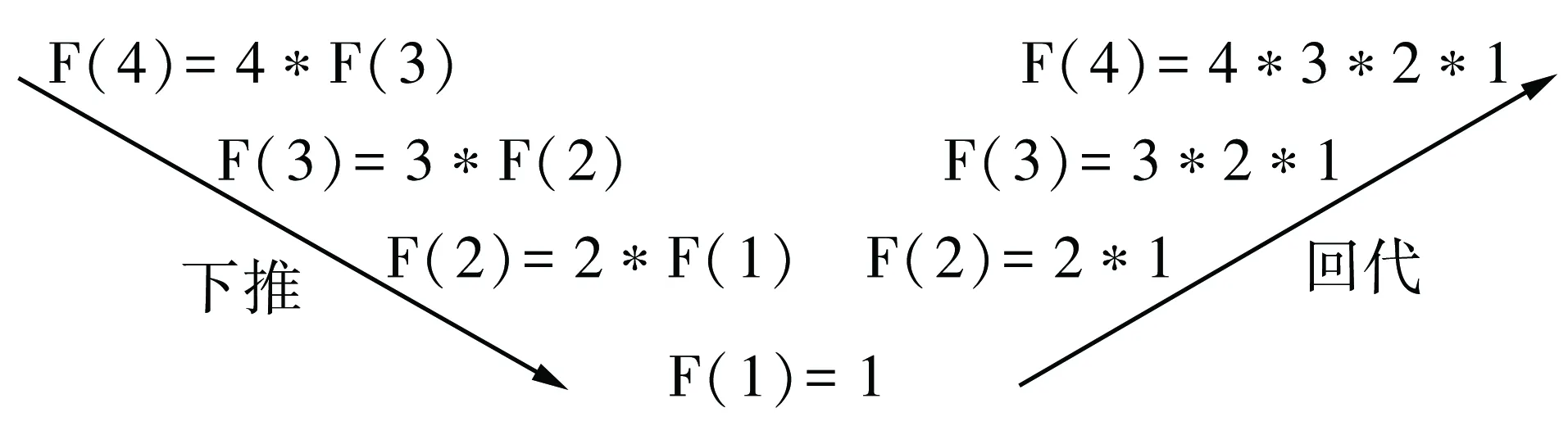
5 递归转换为非递归
6 结束语

