基于针孔成像原理的监控摄像机标定方法

谯 帅

（四川大学网络空间安全学院，成都 610207）

0 引言

随着计算机视觉技术的快速发展，利用视频监控来进行安防工作的应用越来越普遍。通过实时分析监控视频画面内容，对危险行为做出预警是基于计算机视觉的安防工作的主要任务。在实际应用中获取目标的实际位置往往是危险行为识别的基础。但是从视频画面中获取的是目标的像素坐标位置，需要通过摄像机标定将其转化为世界坐标系位置。摄像机标定的目的就是建立从图像像素空间到现实世界空间的映射，研究摄相机标定的方法首先需要研究摄像机成像的原理和过程。因为存在摄像机畸变的问题，这种映射通常不是线性的。但实际运用中我们通常用线性关系来近似模拟，表达为：［像］=M［物］。摄像机标定问题即求解M的过程。

1 相关工作

一般摄像机标定可以分为三种方式。

传统的摄像机标定方法通过特定的标定道具来实现。通过标定道具上的三维坐标点与对应图像上的坐标之间的关系，来获取相机模型的参数。传统摄像机标定方法精度比较高且适用于任何相机模型。但标定中必须用到精准的标定道具，且标定过程费时费力。常用的传统摄像机标定方法有双平面标定法、Tsai 两步法等。

主动视觉摄像机标定方法主要是利用已知的摄像机的运动信息，根据运动时图像的变化来计算相机参数，但不适用于摄像机运动信息无法得到的情况。

摄像机自标定的方法只依靠固定摄像机拍摄图像中相同目标点的对应关系来实现摄像机自动标定。实现方法灵活，应用起来方便，但场景依赖度高，通常方法只适用于一种特殊场景。

也有一些综合的方法，如张正友标定法，结合了摄像机自标定方法和传统摄像机标定方法的优点。吴建平等则利用标准化的车道线长度和车道宽度进行自动标定。但不管哪种方法都比较麻烦，要么需要专业人员使用特定标定道具，要么针对于某一种特定场景。

实际安防监控场景中，摄像头的角度往往根据需要会发生变化，每次变化后都要重新进行标定。而摄像机操作人员往往是非专业人员，加之监控场所人员活动复杂，上述方法在部署上存在一定困难。本文在研究摄像机成像原理和一般视频监控特点的基础上，提出了一种基于针孔成像原理利用世界坐标已知固定点位置的快速标定方法。

2 算法实现

在实际情况中，摄像机因其品质的不同，以及摄像距离和目标的位置而存在不同程度的畸变情况。摄像机的主要畸变有两种，一种是径向畸变（Radial Distortion），另一种是切向畸变（Tangential Distortion），本质上描述的是直线在投影过程中产生的偏移，这种偏移使直线经过投影就不再是一条直线。径向畸变通常源于摄像头镜头形状的误差，切向畸变通常源于摄像机的组装过程，如图1所示。除了径向畸变和切向畸变，还存在其他类型的畸变，但一般来讲以这两种畸变最为显著。

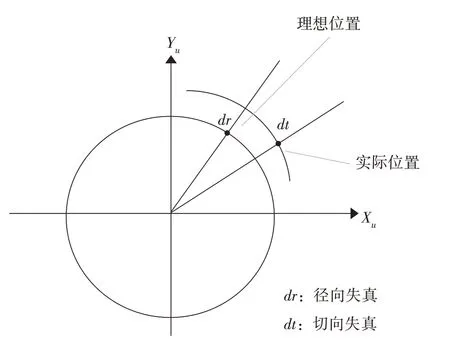
图1 径向畸变和切向畸变

考虑到监控摄像头架设高度通常不会太低，且使用的是高精度的CCD 摄像头，畸变情况比较小，而一般监控场景下定位并不要求非常精确。因此，在大部分情况下可以忽略摄像机畸变的影响，以采取简易的方式进行标定，提高系统的易用性。

2.1 坐标系转换

世界坐标系（World Coordinate）是描述客观世界的笛卡尔直角坐标系，其原点可以任意设置，通常表示为（x，y，z）。

相机坐标系（Camera Coordinate）与世界坐标系相对应，描述客观世界经过小孔成像后的位置。它的原点与摄像机光心重合，轴与轴的方向与相面两边的方向一致，轴与摄像机的光轴重合。表示为（，，）。世界坐标系与相机坐标系的关系可以表示为：

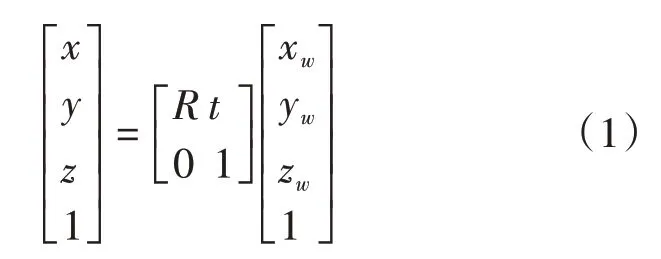
其中表示图像旋转，它是一个3×3 的矩阵，也叫旋转矩阵（Rotation Matrices）。表示图像平移，它是一个3 维列向量，也叫平移向量（Translation Vectors）。

像素坐标系（）即我们日常图像处理时用到的坐标系，它的原点与图像的左上角重合，轴和轴沿着图像的两边延伸。因为它的度量单位是像素点，所以是整数。整数无法直接与现实世界坐标相对应，所以需要建立图像坐标系（），它的单位是毫米。它的原点是图像中点，轴、轴平行于像面两边。像素坐标系与图像坐标系之间的关系如图2所示。

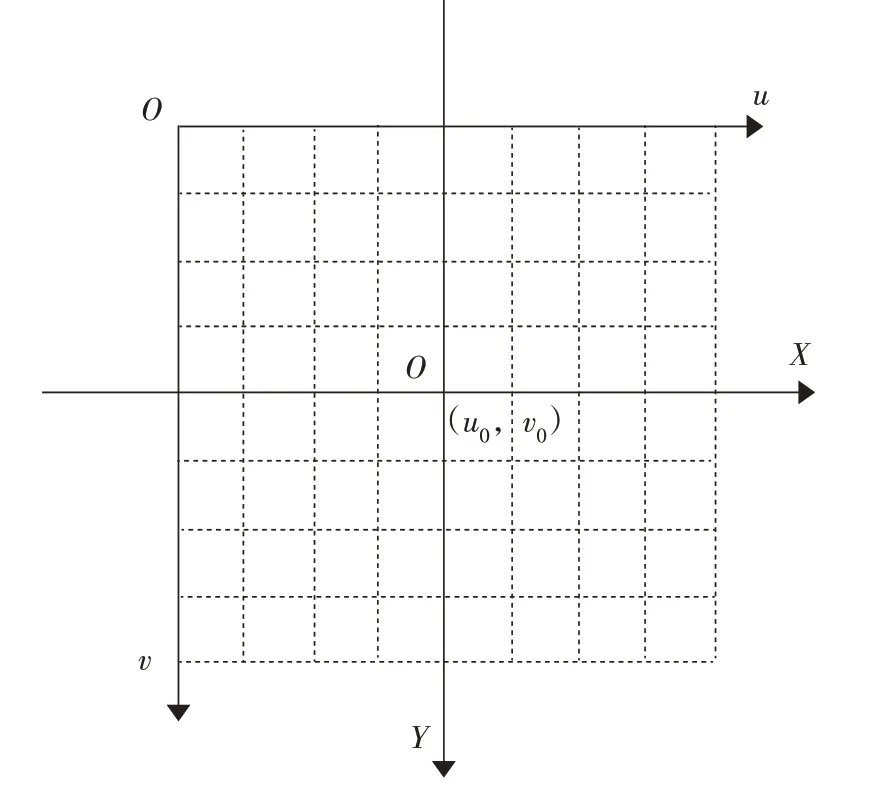
图2 像素坐标系与图像坐标系

用，分别表示一个像素点沿轴和轴占据的大小（毫米），（,）表示图像坐标的原点，他们之间的关系可以表示为：

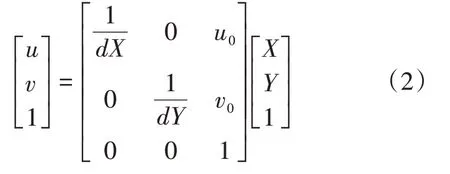
2.2 针孔成像原理

在不考虑畸变的情况下，摄像机成像的理想模型为针孔模型，如图3所示。光心即镜头的中心，亦即针孔的位置。光轴即经过光心与感光平面垂直的直线，图中与轴重合。光轴与感光平面的交点为图像中心。代表焦距，即针孔到感光平面的距离。

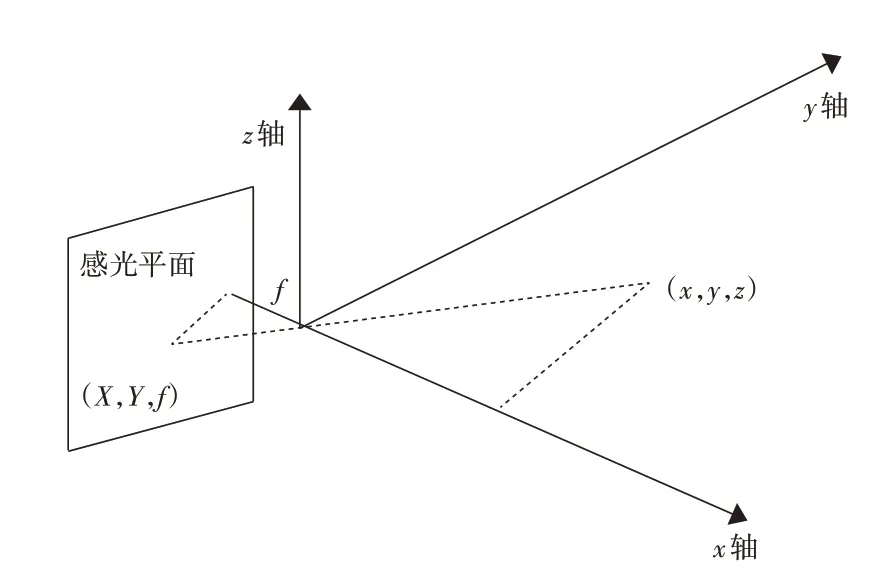
图3 针孔成像模型

不妨假设世界坐标系与相机坐标系平行，（，，）代表现实空间中任意一点的相机坐标系坐标，（，）代表该点在感光平面的投影。根据相似三角形的原理有以下等式：

将其表达为矩阵形式可以写为：

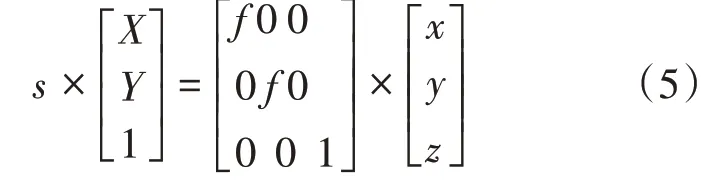
其中为平衡元素个数引入的因子，也称为比例因子。上式也可以写为：

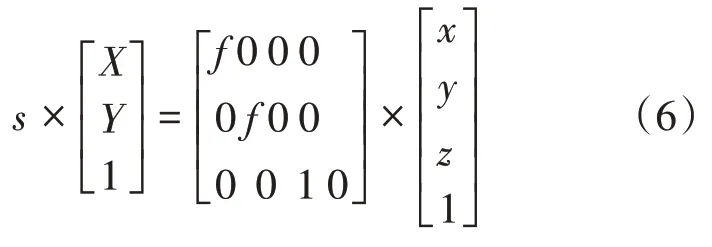
将式（2）、式（6）与式（1）联立，即可从世界坐标系转换到像素坐标系：

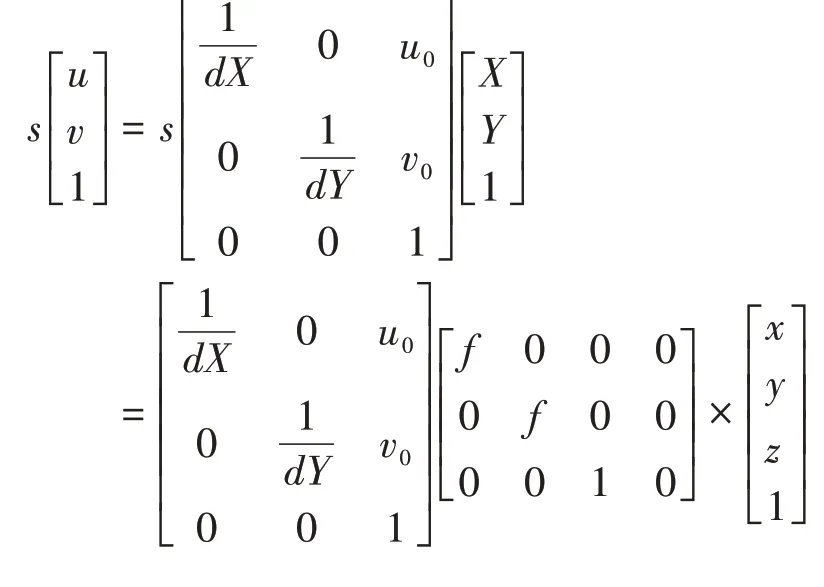
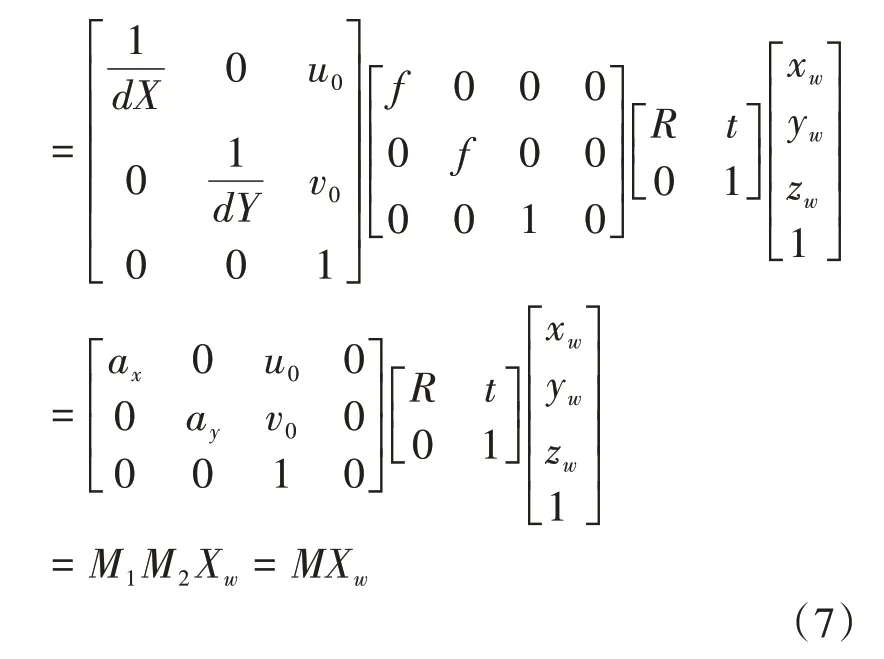
a=/称为轴 尺 度因 子，a=/称 为轴尺度因子。为摄像机的内部参数矩阵，为摄像机的外部参数矩阵，统称为摄像机的投影矩阵。

2.3 基于针孔成像原理的标定方法

将式（7）写为：

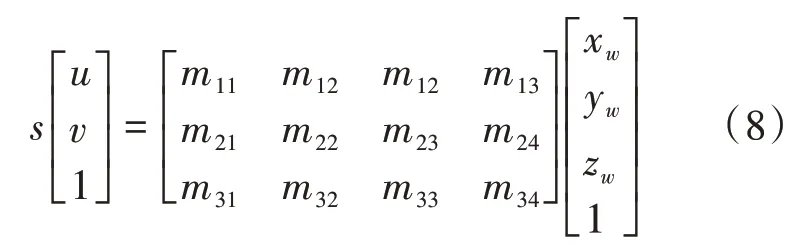
其中，(,)是图像像素坐标，(x,y,z)是世界坐标。在大部分监控场景中目标位于同一平面，例如室内地板或室外平面，目标起伏可以忽略不计，故将上式中z置为0，可写为：

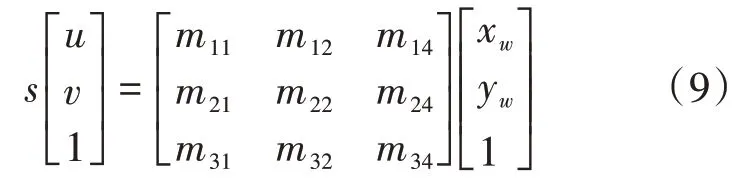
再进一步简化参数。s 作为矩阵的倍乘可以直接移入右边矩阵消去，同样的道理我们可以设=1，并不会对上式运算结果产生影响。所以可将上式写为：

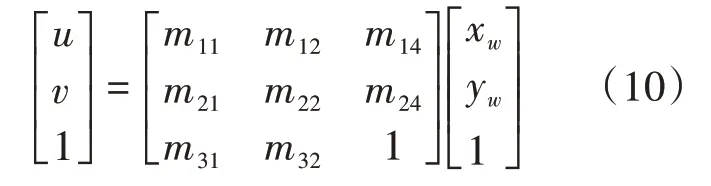
经过恒等变形，相机参数总共有8 个。显然，通过真实世界中道路平面的最少4个点的世界坐标，并找到他们在图像空间中的坐标位置，我们可以建立8 个方程，求解出这8 个参数，进而完成摄像机的标定。

下面介绍实际环境中如何使用本方法简便快捷地完成标定工作。图4 是用Pyhton 自带的Tkinter 库实现的监控摄像机标定界面。显示的是典型的某单位大门监控截取的画面。

图4 监控摄像机标定界面

先需要选取至少4个固定的目标点，再到现地去测量他们的距离并算出对应的世界坐标。通常可选取地面明显的固定目标作为标定物，且即使摄像头角度调整他们通常也还在镜头之内，避免重复现地测量。本系统默认选取地面标线4个点如图4所示。经实地测量点1、点2距离为130米，点3、点4距离为11米，点1到点3、点4连线距离为17米。以点1为世界坐标系原点，1至3方向为轴，则4 个点的坐标可表示为1（0，0），2（0，130），3（-5.5，17），4（5.5，17）。这样便确定到了世界坐标系的4个点及其坐标。

接下来在系统图形设置界面输入这四个点的坐标，并依次在视频截图画面点选1、2、3、4这四个点，程序即可在后台自动获得这四个点的像素坐标，并计算出变换矩阵，存储在配置文件中供其他模块调用。在图4 所示监控画面中，像素坐标分别为1（1122，496），2（140，61），3（273，284），4（831，233），经计算得到的变化矩阵为：

［-9.1323 20.616 20.952］

［ 5.807 26.064 -19443］

［ 0.0029394 -2.172 1］

即使摄像头角度改变，也只需要重新在视频截图中再次点选这几个点，即可简单快速完成摄像机标定工作。具体方法如下：在摄像头标定文本框中，会依次显示用于标定的实地坐标和图像像素坐标。点击“修改”按钮后，需要在文本框中输入至少4 个实地坐标（世界坐标系），默认不输入的话，表示实地坐标继承上一次的设置。输入完实地坐标点击“确定”按钮，按钮变为灰色并显示“在图中依次标出这些点”。同样，在左侧画面中依次点击实地坐标对应的点，会实时显示为深红色小圆点并配有数字编号，点击右键可撤销上一步选择的点，并在画面实时显示。当点选的点与输入的点个数达到一致时，再次点击鼠标左键将提示“标定完成”。点击“确定”后，文本框将显示新的标定数据。如图5所示。

图5 摄像机标定文本框内容变化

3 实验

3.1 路面标定实验

选取实地坐标系中轴值为-5.5、0、5.5，轴值为0～130间隔为10的14个值，根据标定结果可画出42 个均匀分布于道路平面的坐标点。如图6所示。

图6 不同角度标定结果显示

两种不同摄像机角度下的路面标定情况。将与轴平行的3 个点分别用线段连接起来，可得向实地轴方向扩展的间距10 米、宽11 米的14 条平行线。可以看到线条均匀覆盖了道路平面，没有出现明显变形。所有横向线段两侧都在路面白线上，表明轴距离上的准确性。图像上距离最宽两条直线的距离经实地测量确为10米，实地原点和（0，130）点与相应标定点重合，表明了轴距离上的准确性。

3.2 固定点测距实验

实验测量了摄像机在两种不同角度下，相同实地目标点A、B、C、D 之间的距离，所有测量结果实时计算并显示在交互图形界面上，如图6所示。测量结果汇总于表1。

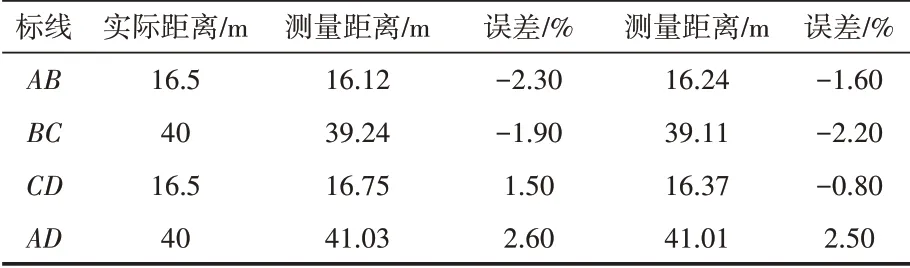
表1 测距结果和误差

从实验结果来看，该标定方法总体效果较好，最低误差0.8%、最高误差2.6%、平均误差1.9%，总体误差在5%以内，可满足一般监控场景下的需求。

但实验中也注意到手工选点会带来一定的误差，所以标定时应尽可能选择菱角分明的目标点，以便提高手工选点的准确性，使得标定更加准精。

4 结语

本文在分析常用摄像机标定方法的基础上，结合视频监控场景特点和摄像机成像的一般原理，提出了一种基于针孔成像原理的监控摄像机标定方法。经实验验证，该标定方法不需要专用标定道具，不依赖于特定场景标志物特征，操作简便、误差较小，为基于计算机视觉的其他安防工作提供了基础，具有实际应用价值。