活用三线合一定理证题

彭现省

等腰三角形底边上的中线、顶角平分线、底边上的高互相重合，亦称为“三线合一”定理.若能灵活运用这一定理，可以巧妙而简捷地证明等腰三角形中的许多问题，下面举例说明，希望同学们能够从中得到有益的启示，提高证题技巧与应用能力，开发创新思维.

1 证明线段相等

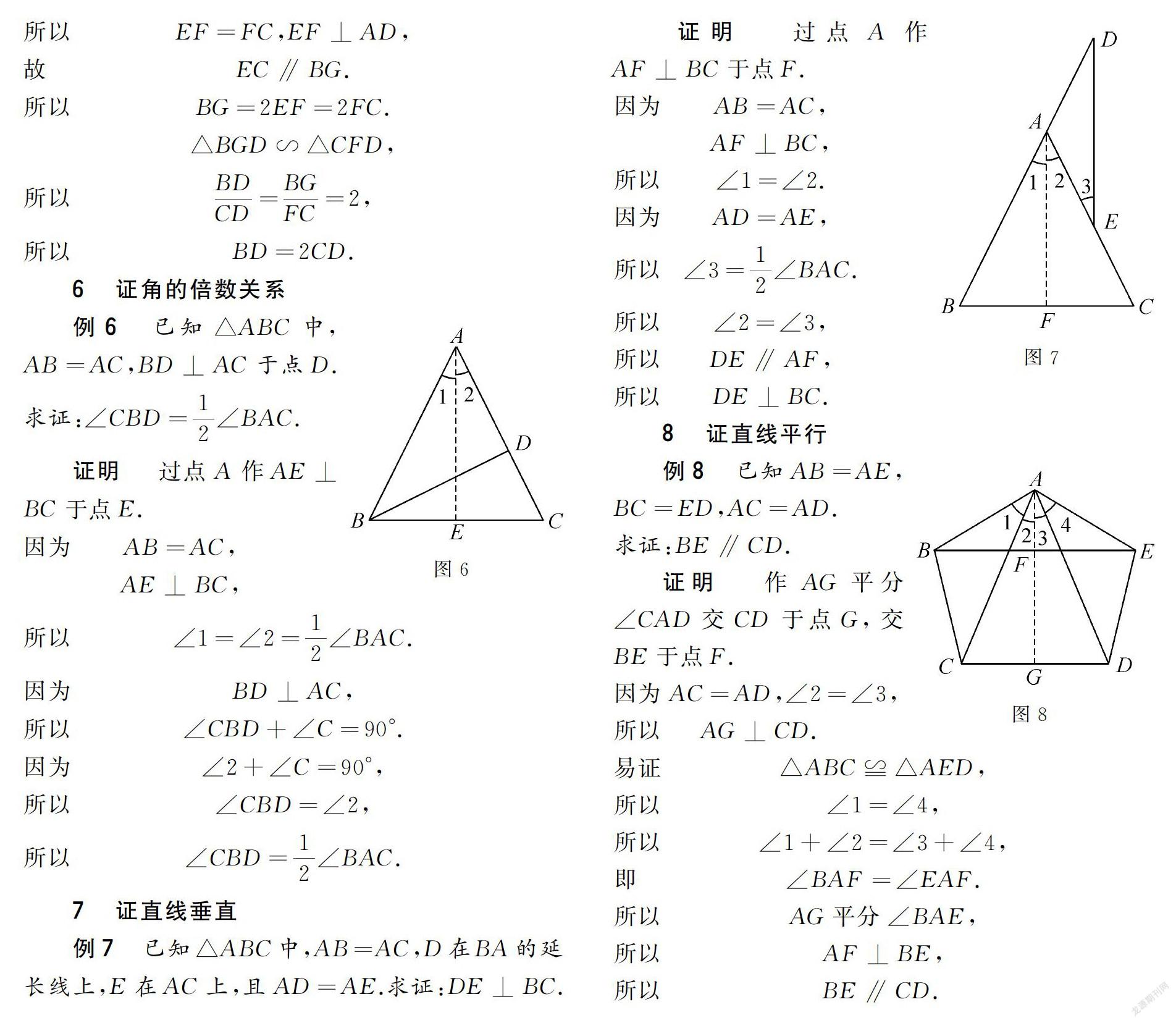
例1 已知△ABC中，AB=AC， BD=CD， DE⊥AB于点E，DF⊥AC于点F.求证：DE=DF.

证明 连接AD，

因为AB=AC，

BD=CD，

所以∠1 =∠2，

即AD为∠BAC的平分线.

因为DE⊥AB于点E，

DF⊥AC于點F.

所以DE=DF.

2 证明线段和差相等

例2 已知△ABC中，AB>AC， AD平分∠BAC，P为AD上的点.求证：AB-AC>PB-PC.

证明 在AB上截取AE=AC，连接PE，CE，CE交AD于点F.

因为AE=AC，

∠1=∠2，

所以AF⊥CE， EF=CF.

所以PE=PC.

因为PB-PE<BE，

BE=AB-AC，

所以AB-AC>PB-PC.

3 证角相等

例3 图3

已知△ABC中，AB=AC， AD⊥BC于点D，DE⊥AB于点E，DF⊥AC于点F.求证：∠DEF=∠DFE.

证明 因为AB=AC， AD⊥BC，

所以∠1=∠2.

因为DE⊥AB，

DF⊥AC，

所以DE=DF，

所以∠DEF=∠DFE.

4 证角的和差大小

例4 图4

已知△ABC中，BE平分∠ABC，AD⊥BE于点D.求证：∠BAD=∠DAC+∠ACB.

证明 延长AD交BC于点F.

因为∠1 =∠2，

AD⊥BD，

所以BF=BA，

所以∠3=∠4.

因为∠4=∠FAC+∠C，

所以∠BAD=∠DAC+∠ACB.

5 证线段倍数关系

例5 图5

已知△ABC中，AB=2AC，∠1=∠2.求证：BD=2CD.

证明 取AB中点E，连接CE交AD于点F.作BG⊥AD交AD的延长线于点G，则AE=AC，则△AEC为等腰三角形.

因为∠1 =∠2，

所以EF=FC，EF⊥AD，

故EC∥BG.

所以BG=2EF=2FC.

△BGD∽△CFD，

所以BDCD=BGFC=2，

所以BD=2CD.

6 证角的倍数关系

例6 图6

已知△ABC中，AB=AC，BD⊥AC于点D.求证：∠CBD=12∠BAC.

证明 过点A作AE⊥BC于点E.

因为AB=AC，

AE⊥BC，

所以∠1=∠2=12∠BAC.

因为BD⊥AC，

所以∠CBD+∠C=90°.

因为∠2+∠C=90°，

所以∠CBD=∠2，

所以∠CBD=12∠BAC.

7 证直线垂直

例7

已知△ABC中，AB=AC，D在BA的延长线上，E在AC上，且AD=AE.求证：DE⊥BC.

证明 过点A作AF⊥BC于点F.

因为AB=AC，

AF⊥BC，

所以∠1=∠2.

因为AD=AE，

所以∠3=12∠BAC.

所以∠2=∠3，

所以DE∥AF，

所以DE⊥BC.

8 证直线平行

例8 图8

已知AB=AE，BC=ED，AC=AD.

求证：BE∥CD.

证明 作AG平分∠CAD交CD于点G，交BE于点F.

因为AC=AD，∠2=∠3，

所以AG⊥CD.

易证△ABC≌△AED，

所以∠1=∠4，

所以∠1+∠2=∠3+∠4，

即∠BAF =∠EAF.

所以AG平分∠BAE，

所以AF⊥BE，

所以BE∥CD.