基于乐队花车效应的观点动力学模型及其实证研究

徐涵,成思,沈浩

（1.华中科技大学新闻与信息传播学院，武汉 430074；2.中国传媒大学媒体融合与传播国家重点实验室，北京 100024）

1 引言

近年来，随着互联网与通信技术的高速发展，空间与时间对意见交换的限制被大幅削弱，跨时空对话、与素未谋面的陌生人交流变得轻而易举，人们能够更加便捷地分享自己的观点、交流彼此的意见。个体之间进行观点交互的社交网络也因此变得愈发庞大复杂，各种不确定性因素随之出现，使得舆论的演变充满了不可控性，给舆情管理带来了各种挑战。

观点动力学主要研究复杂网络中的动态问题，其研究成果在舆情管理领域具有重要的实际应用价值，可以帮助应对新时代的舆情管理挑战。在不同的观点动力学模型中，考虑有界置信度的Hegselmann-Krause（HK）模型被广泛应用于模拟各种真实情况，尤其是公众意见演化。利用HK模型，我们可以模拟不同情况下的公众意见演化过程，预测舆情事件发生后的舆论发展方向，为有关部门的舆情管理工作提供理论依据和技术支撑，辅助其制定舆情应对方案。

尽管自经典HK模型提出以来，许多学者已经对其进行了诸多改进研究［1-4］，但仍有许多会影响意见演变的因素尚未被纳入模型的考虑范围，比如在当今社会高频出现的乐队花车效应（Bandwagon Effect）的影响就仍未被考虑其中。因此，为了使观点动力学模型更加符合舆论演化的实际情况、基于模型产出的舆情应对方案更具有价值，本研究基于乐队花车效应对经典HK模型进行扩展，提出了一种新的基于乐队花车效应的观点动力学模型（Bandwagon Effect-Based Hegselmann-Krause Model，BEHK模型），并通过仿真实验进行了实证研究，验证新模型的有效性。

2 相关研究

在观点动力学的发展过程中，最初，研究者们提出了很多经典模型来研究观点演化过程。这些经典模型可以按照观点值的类型被分为离散观点演化模型和连续观点演化模型两大类。其中，经典的离散观点演化模型有投票者模型（Voter Model）［5］、多数裁定模型（Majority-vote Model）［6］和劝导者模型（Sznajd Model）［7］等；连续观点演化模型主要有谈判者模型（Deffuant Model）［8］和 HK 模型［9］。

由于离散观点演化模型认为个体的观点是“非黑即白”的，而在大部分舆情事件中，个体的观点往往不会如此绝对，因此本研究选择认为个体观点值可以在一定区间内连续变化的连续观点演化模型作为研究的基础模型。而在经典的连续观点演化模型中，谈判者模型认为个体在更新意见时仅和与其观点相近的一个个体相互作用，HK模型则认为个体会与邻居中所有观点相近的个体进行相互作用。考虑到当今社会的舆情事件多发于互联网，个体往往处于一对多的状态，因此本研究选取更贴合情况的HK模型作为具体的基础模型进行改进研究。

在经典的HK模型中，个体只与那些意见在其置信范围内的邻居进行交流，并在意见更新时将这些人的平均意见作为自己的新意见；如果没有邻居，个体意见将保持不变。给定一个社交网络G=(V,E)，其表达式如式（1）所示。

其中Oj(t)表示个体j在t时刻的意见；Ni(t)表示t时刻可以与个体i交换意见的邻居集合，其范围如式（2）所示，(2)中εi代表个体i的置信范围。

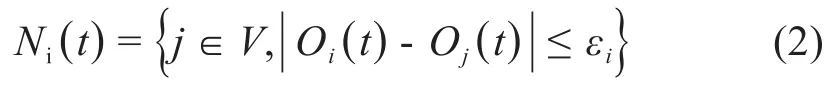
目前，许多研究者致力于通过引入新的影响意见演化的因素来对经典HK模型进行改进。在信任因素的影响方面，Fu等［10］认为现实世界中个体对自己和邻居意见的信任程度存在差异，当个体更新意见时，独立考虑自己的意见会更合理，基于此提出了修正的HK模型（MHK模型），其表达式如（3）所示。

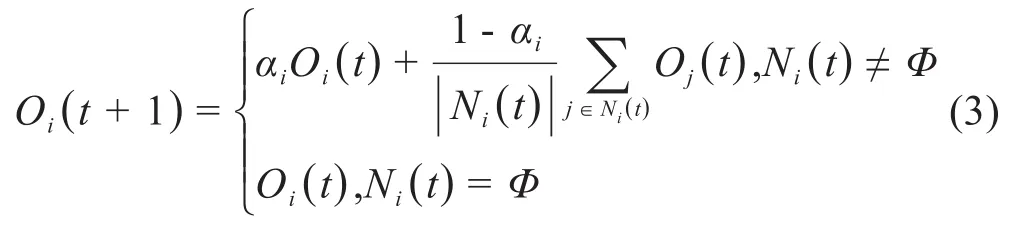
其中αi∈［0,1］代表个体对自己观点的信任程度，邻居集合Ni(t)的范围在经典HK模型的基础上剔除了个体自己。张亚楠等人［11］考虑到人与人相互交往过程中存在心理关系上亲疏程度的差异，引入参数关系度，提出了一种新的关系HK模型。苏炯铭等人［12］发现连续观点动力学模型中缺乏对个体信任及其观点的不同权重的考虑，引入个体间的信任度和观点间的相似度两个参数，基于HK模型，将有限信任假设扩展为有限影响假设，建立了带权重的观点更新模型。回顾相关文献，可以发现已有研究涉及较多的是个体与个体间的内部信任对观点演变的影响。

而所谓乐队花车效应［13］，来源于心理学的概念，指的是一种行为模式在群体中的加速扩散，一个人做某件事的概率随着已经这么做了的人的比例增加而增加。当它应用于观点动力学领域时，指个体对多数意见会持更信任的态度，个体在群体的引导或施加的压力之下会怀疑并改变自己的观点，使其与群体中大多数人的意见保持一致。也就是说，在个体之间进行意见交互从而更新观点的过程中，当个体意见与群体意见相差大时，个体会更信任群体意见，个体对意见的信任程度受到意见与群体意见差异的影响。Wang等［14］用阈值模型对集体把关中的人际效应和乐队花车效应进行建模，发现集体把关人中的乐队花车效应是在线新闻传播的主要驱动力，为理解集体把关对信息传播的影响做出贡献。杨超［15］基于两个真实案例分析了突发事件传播中的乐队花车效应，并从政府、意见领袖和大众三个层面对此提出了解决建议。

基于乐队花车效应，本研究提出在经典HK模型中引入群体意见因素，并提出在意见更新过程中，将个体对其邻居意见的信任系数建模为当前时刻个体自身意见与群体意见之差的函数关系。与现有的研究相比，本文的创新点在于考虑到了网络中个体对外部群体环境的信任及个体意见与群体意见的差异对个体意见信任程度的影响，从而能够更好的对社交网络上的观点演化进行建模。

3 模型结构

本研究将网络中的个体分为普通个体及意见领袖个体，所有个体的初始意见值在［-1,1］随机分布。给定一个社交网络G=(V,E)，这些个体在意见演化过程中遵守以下规则：

①群体意见受所有个体意见影响，它可以是当前时刻所有个体意见的均值。用Xc(t）表示t时刻的群体意见，则其表达式为式（4）：

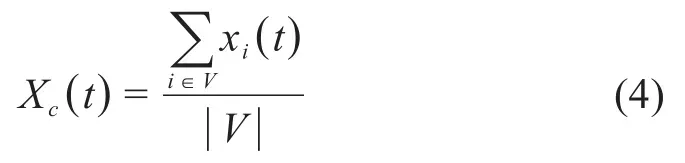
其中xi(t)代表个体i在t时刻的意见值。

②个体中存在一种固执个体，其意见值始终等于初始值。

③非固执普通个体只会接触置信范围内的普通邻居，但会接触置信范围外的意见领袖。在意见更新时，其意见受上一时刻自己的意见、普通邻居的意见、相邻意见领袖的意见和群体意见的影响，表达式如式（5）所示。

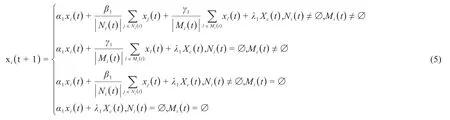
其中Ni(t)代表t时刻与个体i相邻且在置信范围内的普通个体集合，Mi(t)代表t时刻与个体i相邻的意见领袖个体集合，α1、β1、γ1、λ1分别代表个体对自己的意见、普通邻居的意见、意见领袖的意见、群体意见的信任程度，α1+β1+γ1+λ1=1。

基于乐队花车效应，个体对多数意见会持较信任的态度，所以当个体意见与群体意见相差大时，个体会更信任群体意见，即λ1大，α1小；当个体意见与群体意见无差异时，个体对自身意见与群体意见的信任程度持平，即α1=λ1，可以用公式（6）表示这种关系。

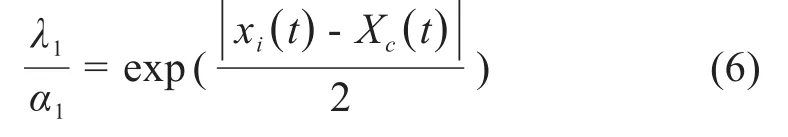
④在意见更新时，非固执意见领袖个体的意见受上一时刻自己的意见、相邻意见领袖意见、群体意见影响，表达式如式（7）所示。

其中Nk(t)代表t时刻与意见领袖个体k相邻的意见领袖个体集合，α2、β2、λ2分别代表意见领袖个体对自己的意见、其他意见领袖的意见、群体意见的信任程度，α2+β2+λ2=1。与（6）类似，α2与λ2的关系如（8）所示。

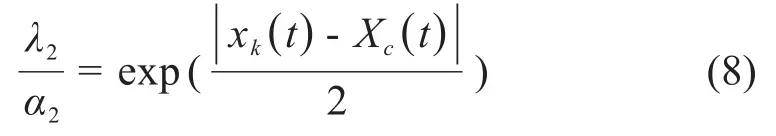
非固执普通个体在进行意见更新时，可能的个体连接情况和对应公式初始权重分配如下所示：

①非固执普通个体的意见受到自己的意见、普通邻居的意见、相邻意见领袖的意见和群体意见的影响，则可能的初始系数为：

α11=0.2,β11=0.1,γ11=0.4,λ11=0.3

②如果非固执普通个体没有在置信范围内的普通邻居，则其意见只受自己的意见、相邻意见领袖的意见和群体意见的影响。可能的初始系数为：

α12=0.2,β12=0,γ12=0.5,λ12=0.3

③如果非固执普通个体没有与之相连的意见领袖，则其意见只受自己的意见、普通邻居的意见和群体意见的影响。可能的初始系数为：

α13=0.2,β13=0.5,γ13=0,λ13=0.3

④如果非固执普通个体没有在置信范围内的普通邻居和与之相连的意见领袖，则其意见只受自己的意见和群体意见的影响。可能的初始系数为：

α14=0.4,β14=0,γ14=0,λ14=0.6

以上是初始权重分配的一种可能情况。这样设置的原因是：由于乐队花车效应的存在，λ1＞α1更有可能出现；同时由于这是初始阶段，个体对群体意见的感知并不明显，所以仍然可能存在大于λ1的权重。

非固执意见领袖个体在进行意见更新时，可能的个体连接情况和对应公式初始权重分配如下所示：

①非固执意见领袖个体的意见受到自己的意见、相邻意见领袖的意见和群体意见的影响，则可能的初始系数为：

α21=0.3,β21=0.3,λ21=0.4

②如果非固执意见领袖个体没有相邻意见领袖，则其意见只受自己的意见、群体意见的影响。可能的初始系数为：

α22=0.4,β22=0,λ22=0.6

初始权重分配这样设置的原因与前文相同。

4 实证研究和结果分析

4.1 实验设置

数据集：为了验证BEHK模型的有效性，我们在两个人工生成网络（BA无标度网络和WS小世界网络）和两个真实物理世界网络（ego-Facebook网络和feather-lastfm-social网络）中进行了观点演化实验。其中BA网络和WS网络系通过相关网络生成算法生成，ego-Facebook网络和feather-sastfm-social网络获取自斯坦福网络分析平台。ego-Facebook网络数据集由Facebook的朋友列表组成，数据来源于使用Facebook APP的调查参与者；feather-lastfm-social网络是来自亚洲国家的LastFM用户的社交关系，于2020年3月从公共API中搜集。这4个网络的基本特征如表1所示：

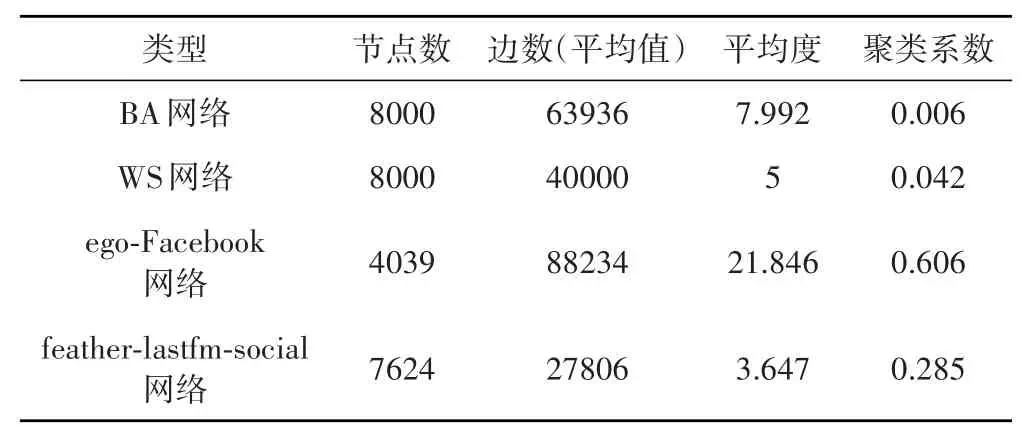
表1 四种复杂网络的基本特征

实验参数：仿真实验中使用的参数如下：

-意见领袖比例：θ=2%、θ=10%

-个体置信度：ε=0.2、ε=0.6、ε=0.9

-初始状态下个体对群体意见的信任系数：λ=0.1、λ=0.01、λ如第3部分所示

-在群体意见计算公式中，意见领袖意见与普通个体意见的权重比：η=1、η=3、η=10

4.2 BA网络实验结果

在有8000个节点的BA网络中进行模拟实验，为意见领袖比例θ和个体置信度ε赋不同的值，观点演化结果如图1所示。从图1整体可以看出，考虑乐队花车效应，在群体观点和意见领袖的共同影响下，无论θ和ε如何变化，除固执个体外，其他个体的观点都能在较短时间内达成共识。当θ=0.02和ε=0.2时，我们可以看到，固执个体在整个过程中都保持初始意见不变，而其他非固执个体在第11天的时候以极小的意见区间达成共识。当ε值从0.2增加到0.6，非固执个体在第9天达成共识，且共识意见区间增大。当ε值增加到0.9时，非固执个体在第7天达成共识，达成共识所需的时间进一步减少，共识意见区间进一步增大。

图1 不同意见领袖比例和个体置信度对BA网络中观点演化的影响。

4.3 WS网络实验结果

在有8000个节点的WS网络中进行仿真实验，为个体置信度ε和个体对群体观点的初始信任系数λ赋不同的值，意见演化结果如图2所示。与BA网络中的仿真结果相似，非固执个体可以在较短时间内达成共识。θ=10%时，ε值从0.6降至0.2，非固执个体达成共识所需的时间变长，最终的共识意见区间变窄。当θ=10%和ε=0.6时，图2(a)、(c）和（d）分别为λ如第3部分所示、λ=0.1和λ=0.01时的仿真结果。我们可以看到λ越小，初始阶段的观点变化越慢。当λ小到一定程度时，就会出现“折角”现象。这是因为在初始阶段，当群体观点的影响力降低时，个体就会更多地考虑自己和邻居的意见，他们的自信水平会相应提高，观点的变化幅度会减小。

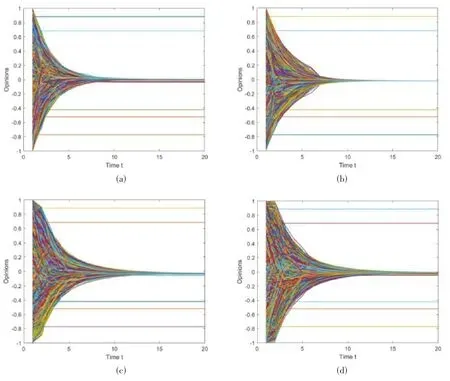
图2 不同个体置信度和个体对群体意见的初始信任系数对WS网络中观点演化的影响。

4.4. ego-FaceBook网络实验结果

在有4039个节点的真实ego-FaceBook网络中进行同样的仿真实验，意见演化结果如图3所示。与BA网络和WS网络中的实验结果相似，给定不同的θ和ε值，非固执个体可以在较短时间内达成共识，且达成共识所需的时间和最终共识观点区间与ε值有关，此结果不受网络规模的影响。

图3 不同意见领袖比例和个体置信度对ego-FB网络中观点演化的影响。

4.5 Feather-lastfm-social网络实验结果

为个体置信度ε赋不同的值，并在群体观点更新计算公式中调整意见领袖的意见权重，在有7624个节点的真实feather-lastfm-social网络中进行相同的仿真实验，观点演化结果如图4所示。对比图4(a）和（b）可以看出，与上述三种网络的仿真结果相似，几乎所有的非固执个体都能在较短时间内达成共识。θ=2%时，ε从0.6减小到0.2使非固执个体达成共识需要的时间增加，最终共识观点区间变窄。但与上述情况不同的是，在这个真实网络中，有大量个体位于网络边缘。因此，在观点演化的过程中，由于缺乏意见的交换，会有极少数的个体被随机孤立。在图4(a）和（b）中，我们可以看到每个图中都有一个孤立个体，他们的最终观点与群体观点不一致。图4(a)、(c)、(d）分别为η=1、η=3、η=10时的模拟结果。我们可以看出，在群体观点更新计算公式中，意见领袖观点与普通个体观点的权重比例不会影响最终达成共识的结果，但共识观点区间大小是随机的。

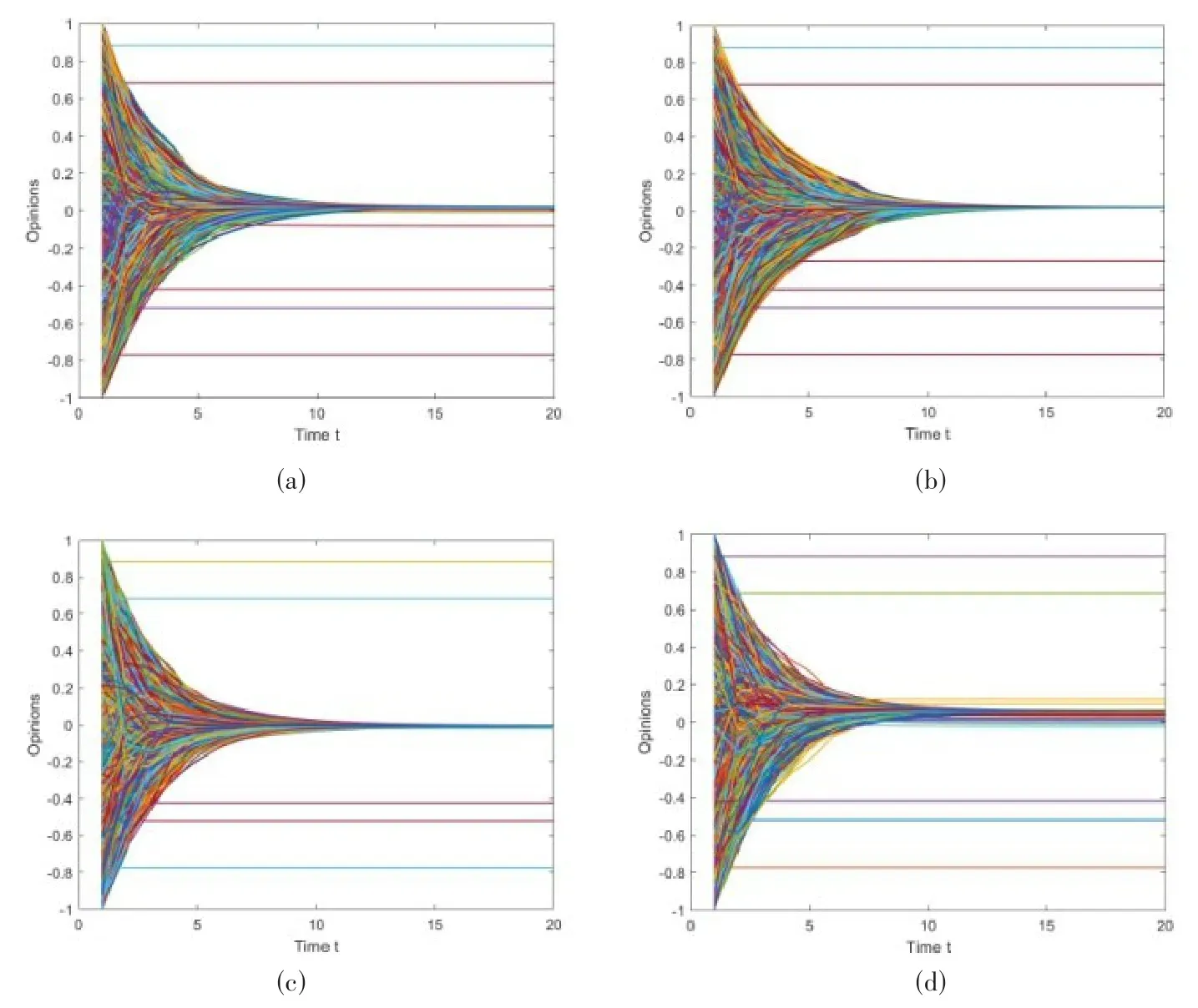
图4 不同个体置信度和群体观点更新公式中意见领袖观点权重对feather-lastfm-social网络中意见演化的影响。

5 结语

本研究基于乐队花车效应，考虑群体观点和信任程度等因素，提出了一种新的基于乐队花车效应的Hegselmann-Krause观点动力学模型。实证分析结果表明，考虑乐队花车效应，在群体观点和意见领袖的共同影响下，无论θ和ε如何变化、网络规模如何，除固执个体和孤立个体外，其他个体的意见都能在较短时间内达成一致。个体置信度越小，达成共识所需的时间越长，最终的共识区间范围越窄。此外，个体对群体意见的信任程度也会影响意见变化幅度。在初始阶段，个体对群体意见的信任系数越低，意见变化幅度越小。

本研究已经在两个人工生成的网络数据集和两个真实的网络数据集上得到了广泛的实验结果，但后期还可以在规模更大的真实社交网络数据集中进行实验，以进一步验证所提出模型的有效性与鲁棒性；此外，在大量的实验中，我们发现除部分固执个体和孤立个体外，群体中的最大观点值会随着时间的推移而严格降低，而群体中的最小意见值会随着时间的推移而严格增加，因此群体意见在有限的时间内会不可避免地趋于一致。在今后的工作中，如何严格证明模型的收敛性以及明确收敛时间下界，值得进一步研究。