三角形三边关系之“三探”

江苏海安市城南实验小学（226600）张小丽

【教学案例】

师（课件出示形形色色、形状各异的图形）：你能识别出三角形吗？

（学生很快找到了三角形，而且找得很齐全）

师：你们寻找的依据是什么？又凭借什么断言它们是三角形？

生1：只要含有三条边、三个角的几何图形就可以认定为三角形。

生2：不对，应该说由三条线段首尾顺次相接组成的图形叫作三角形，而三角形含有三条边、三个角和三个顶点。

师（图片演示）：由三条线段首尾顺次相接围成的图形是三角形。

师：假若提供三条线段，你有把握能围成一个三角形吗？

生3（胸有成竹）：能。

（教师发给学生8厘米、10厘米、15厘米的竹签各一根，学生上台演示，顺利完成任务）

师（教师再发给学生3厘米、10厘米、15厘米的竹签各一根，学生捣鼓半天，始终无法如愿）：通过刚才的两次尝试，你们有没有发现什么蹊跷？

生4：三根竹签围三角形，有时成功，有时失败。

师：一语中的！那么什么时候会成功，什么时候会失败？这其中到底有什么奥秘？三角形的三边之间是否存在某种不为人知的微妙联系呢？这就是我们本次课的学习重点。

评析：教师利用学生思维中的“漏洞”和思想上的“麻痹”，让学生自行拼接三角形，并且故意配给两组拼接结果截然不同的竹签，制造了认知冲突。在成败得失之间，学生对三角形的三边关系产生了强烈的好奇心。从三角形的表面看，学生最初误认为任意三条线段就能组成三角形，但通过动手拼接，认知结构发生改变，开始意识到三角形的三边之间定然存在某种微妙关系，而这种关系直接决定能不能围成三角形。该教学是较为常见的模式，大部分教师都用这种方法。下面利用“三探”对该教学进行创新性的改进。

一、独立自主探究

【教学片段1】

师：老师给每个小组发一个匣子，匣子里有五根竹签，要求大家通过这五根竹签的拼接，探索出三角形三边的关系。

课件呈现合作须知：

（1）从匣子中存放的五根竹签（长度分别为4厘米、6厘米、8厘米、10厘米、15厘米）中随机抽取三根，试着拼接三角形。

（2）小组共同探究，小组长负责记录数据，包括竹签长度和拼接成败。（见表1）

表1

（3）综合分析本组多次实验的结果，并回答以下问题：如果能够围成三角形，三根竹签需要满足什么条件？什么情况下会拼接失败？

评析：课本的原意是准备四组竹签先让学生操作，然后通过列式比较大小来推导三角形的三边关系，如此设计固然直截了当，但是在操作之后就迫不及待地要求学生列式，从定性分析直接上升到定量分析，未免有些突兀和操之过急。学生被教师牵着鼻子走，被迫去操作、计算，得出的结论自然也不是学生自己发现的。为什么一定要拿两边之和与第三边做比较，比较其他的关系就不行吗？显然，如此探究不过是学生在教师的授意下做出的妥协与顺从。鉴于此，笔者对该部分做了加工和改进，改为“发给学生五根不同长度的竹签，让学生随机抽选三根进行拼接实验，并从中归纳出定律”。这样，学生就能通过操作活动体验到三边之间的长度关系能够左右拼接的成败，然后通过对大量实验数据的对比，从中归纳出三角形的三边关系。

三角形的三边关系是一个抽象的几何关系，是定性分析的结果，那么就意味着无法采用一般的逻辑推理法去推导，因为没有特殊和一般之分，所以无法进行演绎推理，也无法进行合情推理，只能用直观演示法来揭示，即让学生在大量的随机实验中发现不寻常的地方，产生认知冲突：为什么有的竹签可以拼接成三角形，有的却不行。在好奇心的驱使下，学生就会积极主动探究，通过对比观察，理性归纳出三根竹签能围成三角形的必要条件。

二、小组合作探究

【教学片段2】

活动环节：学生4人一组开展探究活动，一人拼接竹签，小组长记录竹签长度和实验成败，其他组员观察数据并综合分析。教师巡检督导，倾听学生意见。

汇报环节：各组派代表上台汇报本组的实验情况，教师综合各组的数据，整理出一份规范的记录单（见表2）。

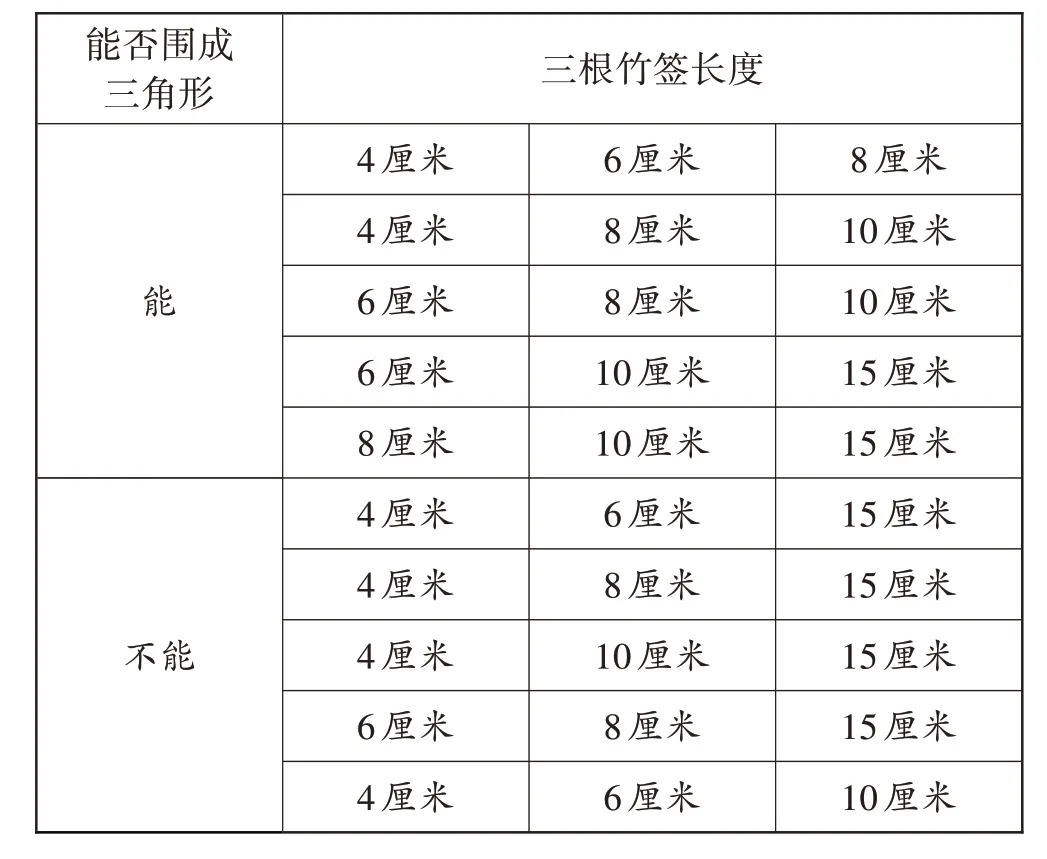
表2

生1：我觉得长度分别为4厘米、6厘米、10厘米的三根竹签也能拼接成一个三角形。

师：真的吗？可否让大家开开眼界。

（由于学具可弯曲，生1拼成了“三角形”。）

生2：生1的竹签有些畸形，凑巧而已。

生3：从理论上讲根本无法拼成三角形，因为两根短竹签的长度加起来等于第三根竹签的长度，两根短竹签连起来会与第三根竹签重合成一条线，无法拱起形成犄角。

师：言之有理，我们来看看动态演示。（动态演示的结果显示：长度分别为4厘米、6厘米、10厘米的三根竹签无法拱起形成犄角）

师：什么情况下三根竹签无法围成三角形呢？

生4：当其中两根短竹签的长度和小于或者等于长竹签时无法围成三角形。

师：那么若要围成三角形，对三根竹签的长度有什么要求呢？

生5：当两根较短竹签长度之和超过第三根较长竹签时，就能拼成三角形。

师：分析得很到位，由此可以推断，三角形的三边必然存在某种关系。

生6：两短边长度之和必然超过最长边。

生7：任意两边之和必然大于第三边，不然就无法构成三角形了。

师：“任意”二字切中了要害，还道明了其中原委。谁能再精简一下？

生8：在三角形中任意两边的和大于第三边。

评析：“纸上得来终觉浅，绝知此事要躬行。”教师直接告知结论，学生未必记得住，就算记得住也未必信服，而学生在动手操作中发现并通过检验证实有效的结论，则会给学生留下深刻的印象。学生通过对操作中遇到的两种截然不同的现象进行对比辨析，发现其中的规律，从而归纳出三角形的三边关系。从发现问题、产生疑问，到收集、整理、分析数据，初步发现操作性的实验规律，然后转化成理论成果，学生在教师的操作指导下，独立完成了一次数学理论研究，不仅掌握了相关知识，而且学到了科学的研究方法。

很多课堂上随机抽取木棒尝试围成三角形的实验，还只是停留在感性认知的层面，在这样的实验中，学生隐隐约约感到三边的差距不能太大，但是又说不清楚到底是多少才合理，无法定量分析出个所以然来。可见完全靠直观法终究无法得出确切的结论，因此数字化的定量探究过程是必要的，只有用数据说话才能令人信服，也最能让规律外显。于是，学生将所选的组合长度记录下来并制成表格后，在大量数据中，学生发现，三边之间的差距其实可以通过算式来具体表达，即最短的两边长度之和不能小于最长的边。当教师指引学生弄清两边之和等于第三边也无法围成三角形的原委之后，学生最终才能下定结论：三角形任意两边之和大于第三边。

三、拓展探究

【教学片段3】

出示（教材第31页第1题，题略）：勾选能摆成三角形的竹签。

生1：第一组和第三组可摆成三角形，因为任意两根竹签的长度之和大于第三根竹签。第二组不能，因为本组有两根竹签长度之和等于第三根竹签。

生2：不用成对逐项筛查，只需直接判断最短两边之和与最长边的大小关系即可一锤定音。

出示（教材第31页第2题，题略）：从下面五根竹签中随机抽选三根，尝试摆出两个不同形状的三角形。

师：拼接前先设想“摆出的三角形会是什么样子”，然后再动手操作，对比一下是否与设想的相符。

生3：我摆出了两个三角形，一个是等边三角形，另一个是等腰三角形。

生4：我摆出了两个三角形，一个是钝角三角形，另一个是锐角三角形。

……

出示题目：如果已知三角形的两条边的长分别是5厘米和8厘米，那么第三边的长度范围是多少？

生1：第三边长度应该介于3厘米和13厘米之间。

师：愿闻其详。

生1：因为三角形任意两边之和要大于第三边，若将8厘米的边作为最长边，第三边加上5就应该大于8，所以第三边就应该大于3；若将第三边作为最长边，那么第三边要小于5+8=13，而5厘米的边不可能设为最长边，因此只需考虑以上两种情况。

生2（若有所思）：8-5=3，8+5=13，第三边就处于这两个结果之间。

师：是不是三角形中任意两边的差都小于第三边呢？大家不妨证实一下。

师：可以借用前面可以围成三角形的三边数据。

出示数据：

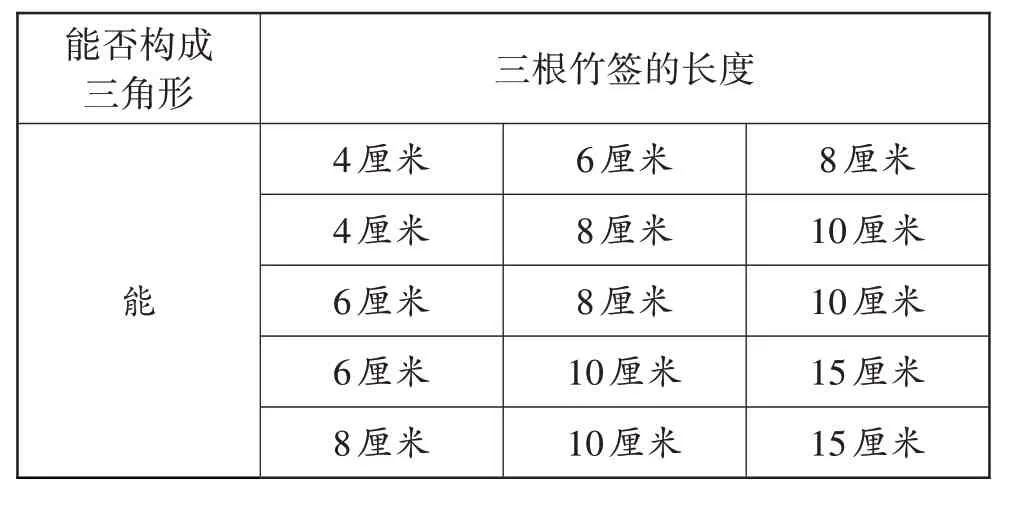
表3

生3（再次回顾前面的实验数据，对照观察发现新结论）：6-4＜8，8-4＜6，8-6＜4，没有一个例外，所以三角形任意两边的差都小于第三边的结论成立。

评析：在研究出三角形任意两边之和大于第三边的定理后，笔者设置开放性问题，给定两边长度，让学生确定第三边长度的取值范围。这次不再是判别能不能构成三角形，而是要通过运算确定边长，引发学生深度思考。这个思考是多向的、全面的，之前只需要直接两两求和进行对比，现在出现一个不确定元素，这个元素既可以作为最长边，又可以作为非最长边，所以会出现一个取值范围，而且需要换位运算，从而引出作差的需要。

应用三角形的三边关系推算第三边的长度取值范围，必须将三角形的三边关系结论进一步拓展，才能得出另一个对称结论——三角形两边之差小于第三边。要想得出第一个基本结论的“姊妹篇”，还得转向定量分析：给定三角形的两边长度，然后根据第一个基本结论推算出第三边的长度取值范围。这个过程对学生来说非常复杂，逻辑性非常强，因为推算出第三边的长度取值范围后，还要再根据三边相对精确的长度关系反推出结论。至此，三角形的三边关系才算彻底明朗，而这个最终结论是在定性分析与定量分析交替进行中得出的。