智能超表面辅助车载边缘计算

刘文帅/LIU Wenshuai，李斌/LI Bin，2

（1. 南京信息工程大学，中国南京 210044；2. 网络与交换技术国家重点实验室（北京邮电大学），中国北京 100876）

当前无线通信技术面临能耗高、覆盖低、无线信道不可控等问题，严重影响了通信服务质量。作为未来6G 的一项空口技术，智能超表面（RIS）得到了广泛关注[1-2]。RIS由一组无源反射元件构成，可通过编程来实时调控各个反射单元，进而控制入射信道的幅值和相位，在功耗和部署成本上具有优势[3]。RIS辅助通信的关键是使用超表面来改变无线传播环境，从而减轻多径衰落和视距阻塞的负面影响。

车载通信是智能交通系统不可或缺的组成部分，它允许汽车与周围环境以及远程实体保持联系，并为车辆提供随时随地的连接服务[4]。由于传播环境复杂，车辆与路边单元（RSU）之间建立的传播链路质量很容易恶化[5-6]。在障碍物遮挡的RSU服务暗区，利用RIS技术为行驶的车辆能够提供间接的视距传输链路，将有望为高能效车载通信提供重要的手段支撑。为了提高车载通信的连通性，文献[7]提出了一种面向高频段的RIS辅助架构，并综合考虑RIS的规模和运行模式，研究了RIS的最优部署问题。文献[8]提出了一种异构车联网，并使用联邦Q 学习最小化网络开销。文献[9]研究了毫米波车联网上行链路速率最大化问题，借助RIS技术提高上行链路性能。文献[10]研究了离散相移约束下的上行链路速率加权和最大化问题，并分别为单用户和多用户场景提供解决方案。文献[11]提出了一个多RIS辅助的多车多天线通信系统，通过交替迭代算法优化发射机的波束成形矢量和每个RIS 的相移，使车载通信服务质量达到最高。文献[12]研究了RIS辅助车联网的频谱共享问题，即多个车到车链路可以复用已被车到基础设施链路占用的频谱，使用中断概率作为评估车载通信可靠性的性能指标。

由于网络环境高度动态变化，使用RIS辅助车联网仍面临着诸多挑战[13-14]。（1）RIS 与车辆之间距离的变化会影响实时信道状态，同时车辆在区域内的滞留时间不同，这些均使得RSU 在优化通信质量的同时，还需要考虑车辆的移动性；（2）在获取相同服务资源的情况下，滞留时间较长的车辆的服务质量会有所下降，因此为尽可能保障服务的公平性，该网络场景下的通信资源需要进行合理分配。未来的状态信息通常难以预知，RSU需要与车辆不断交换各种状态信息，根据即时状态信息进行在线决策。基于深度强化学习（DRL）的方法可以根据当前的环境状态进行决策，对环境的先验信息要求较低。文献[14]考虑到物联网设备能量与计算能力双重受限问题，提出了一种RIS辅助的无线供能移动边缘网络方案，利用双深度Q网络方法联合优化无线传能时隙分配、RIS相移和卸载决策，从而提升能量转移效率和通信效率。考虑到实际的RIS相移，文献[15]研究了联合车辆调度和RIS无源波束成形优化问题，通过深度强化学习和块坐标下降法使暗区车辆的最小可实现比特率达到最大。然而，这些工作对于车载边缘计算（VEC）中RIS辅助通信的研究尚不深入。

随着5G时代人工智能的不断发展，各种时延敏感性、计算密集型的交通应用和服务不断涌现[16]，这给资源有限的设备带来极大挑战。车辆自身的计算处理能力往往不强，难以实现实时高效的数据处理。VEC作为一种新范式将车联网与移动边缘计算两者融合，从而解决车辆自身计算能力受限问题[17-18]。相较于传统移动边缘计算，VEC能为智能交通系统提供更方便的服务，更适用于路边智能基础设施与移动性较强的车辆终端，旨在为海量的交通应用提供随时随地的连接。在这种场景下，更多的系统参数使传输方案的设计变得更难，部署RIS能否带来性能增益还有待研究。基于以上考虑，本文提出了一种基于近端策略优化（PPO）的计算卸载在线优化算法。

1 系统模型

1.1 计算模型

1.2 通信模型

图1 RIS辅助车载边缘计算系统模型

由式（6）可知，当RSU的接收信号信噪比最大时，即：

依据香农公式，时隙n内车辆k的平均卸载速率为：

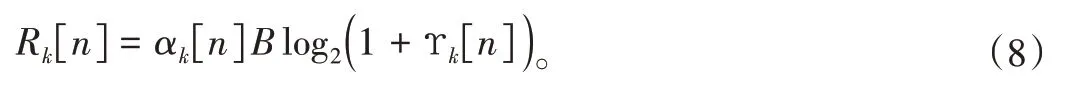
车辆k通过RSU覆盖暗区的平均卸载速率可以表示为：

为简化问题，本文对任一车辆经过暗区所需的时隙数进行上取整操作。

1.3 问题描述

本文面向系统中车辆的服务公平性，通过联合设计时段分配因子、任务卸载比例、RIS相移使所有车辆的最小卸载速率达到最高，因此优化问题可表述为：

2 基于PPO的时段划分与卸载算法

问题（10）是一个多变量高度耦合且存在整型变量NPhard的问题，求解该问题具有很大挑战性。系统中多数状态信息需要在每个时隙内完成即时交换，而现有的凸优化理论设计复杂度高，难以保证决策的实时性。本节提出基于PPO的深度强化学习算法以用于寻求时段划分因子，在给定时段划分决策下，基于凸优化方法处理传输功率与卸载比例。

2.1 RIS相移优化

根据公式（7）和公式（8），可得出RIS最优相移Ψ为：

2.2 传输功率与卸载比例优化

上述问题是关于ρ和p的凸优化问题，可以借助凸优化软件（例如CVX）进行求解。

2.3 基于PPO的时段划分策略

给定Ψ、ρ和p时，式（10）可描述为：

该问题是一个整数优化问题，寻找时段划分策略α的最优解较为困难。本章节提出基于PPO的时段分配在线优化方案，首先介绍DRL 中马尔科夫决策过程（MDP）的基本要素，然后阐述基于PPO的时段划分方法。

2.3.1 MDP基本要素定义

在本文场景中，RSU 不需要任何关于环境的先验信息，环境状态转移概率未知，且状态信息需要即时获取，可建模为无模型、无转移概率的MDP。具体而言，在某个时间步t，环境处于状态s(t)，代理执行动作a(t)，环境转移到可行的后继状态s(t+ 1)，代理接收奖励r(t)，随后t增加1。代理通过观察s(t+ 1)与r(t+ 1)来调整自身策略，不断训练使得累积奖励达到最大。将一个时隙作为一个时间步，下面对状态空间、动作空间和奖励函数进行分别定义。

（1） 状态空间定义：

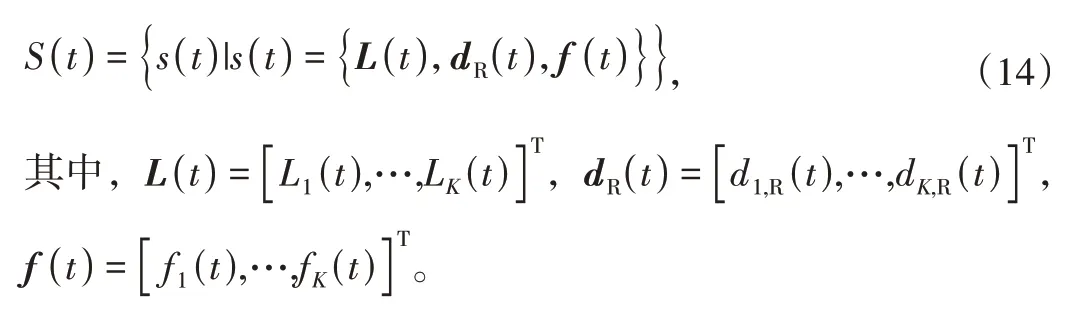
（2） 动作空间定义：

其中，α[n]=[α1[n],…,αK[n]]T，表示时间步t对应时隙n的时段划分因子向量。为便于处理，设置子时隙数U为较大的整数值，同时可近似地将αk[n]作为连续变量处理。

（3） 奖励函数定义：

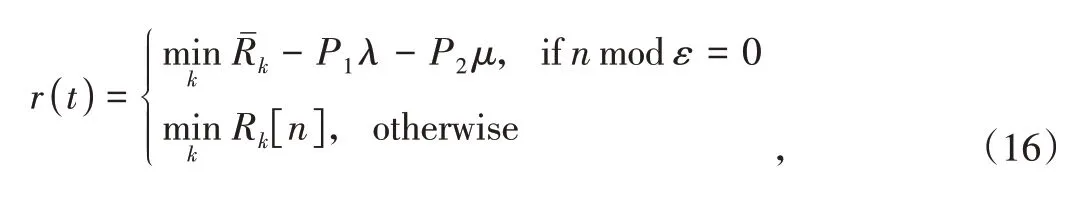
2.3.2 基于PPO的时段划分算法

考虑新动作策略和旧动作策略之间的关系，PPO方法设置了一种新的目标函数，将动作值稳定在近端范围内，使新动作策略的更新可以参照旧动作策略。该方法不仅具有动态决策的优势，还可以快速确定模型的正确优化方向。动作网络根据状态输出动作，与环境交互；评价网络根据状态计算状态价值，估计动作的优劣。

设新、旧动作网络的参数分别为θ和θold，评价网络的参数为ξ，定义每个时间步t的优势函数为：

其中，ϵ是用于控制截断范围的限制参数，其值较小，决定新旧策略之间的差异。目标函数（18）使用剪切概率比，可降低训练难度，被认为是一种优秀的方法。在训练过程中，PPO 算法将状态s(t)输入新动作网络，并输出相应动作a(t)后，从环境中得到奖励r(t)与下一状态s(t+ 1)，此时向回放记忆单元中存入一个完整的经验(s(t),a(t),r(t),s(t+ 1))，随后将s(t+ 1)输入到新动作网络，直到经验池满。RSU 通过与环境交互不断地更新动作网络θ与评价网络ξ，优化自身策略逐渐使奖励值与目标函数达到最大。总的来说，基于PPO的任务卸载算法如下：

算法1. 基于PPO的任务卸载算法输入：最大回合数Ep，每回合最大时间步Smax，学习率lr，限制参数ϵ，GAE参数λ，评价网络参数ξ输出：动作网络参数θ 1.初始化动作网络参数θ，评价网络参数ω

2.FOR episode←1 TO Εp DO 3.初始化：(xk[1],yk[1])、Lk、ck、RSU高度HS、RIS高度HS 4.FOR t ←1 TO Smax DO 5.从环境中获取状态s(t)6.使用πθ根据状态选择动作s(t)7.根据a(t)，求解ρ、p、Ψ 8.计算下一状态s(t + 1)9.根据公式（16）计算奖励r(t)10.存储经验(s[t],a[t],r[t],s[t + 1])11.END FOR 12.FOR t ←1 TO Γ DO 13.计算A^(t)14.END FOR 15.更新动作网络θ，更新评价网络ξ，更新θold ←θ 16.清理经验数据17.END FOR

3 仿真结果与分析

本节在Python 3.6和Pytorch环境下对所提算法进行仿真验证。假设RSU 暗区半径为200 m，车辆出发于x轴负半轴一侧边界，沿x轴正方向行驶，车辆y坐标随机生成该边界上的合理值。RIS 部署于(0,200,70)m，RSU 的位置为(0,500,20)m，服务周期T= 20 s，U= 200，时隙数N= 40，任务数据量Lk∈[106,8 × 106]bits，单位比特平均计算次数ck∈[300,500]cycles/bit，噪声功率σ2=-110 dBm，K1=K2= 10 dB，信道增益γ0=-30 dB。PPO 训练参数如表1所示。

表1 近端策略优化算法参数

图2 对比了PPO 与AC（Actor-Critic）方法在同等学习率与随机数序列下的奖励值收敛曲线。由图2 可知，当回合数增加到500 时，PPO 方法呈现收敛。与之对比的AC 方法虽初期奖励值略高，但收敛到的奖励值与PPO 有较大差异。这表明PPO 是一种能够快速适应动态环境的DRL算法。

图2 训练收敛曲线

当系统中车辆数K=10时，图3对比了PPO、AC与随机分配3种算法下车辆最小速率随RIS元素数变化的情况。可以看出，随着RIS 元素数增加，3 种算法的最小速率均提升显著。其中，本文所提的基于PPO的卸载算法目标值最大，AC 算法与之相比有一定差距，且随着RIS 元素数变化，这种差距渐进增加。随机分配方法性能有较大跳跃，并不是一种适合于实际场景的算法。

图3 RIS元素数对目标值的影响

图4给出了系统中车辆数对不同方案所得传输速率最小值的影响。在RIS元素N=40时，通过所提PPO 算法与优势行动者-评论家（A2C）算法、随机分配策略的性能比较可以看出，所提PPO 算法与A2C 算法两者的性能差距较小。因而，对于A2C 这种改进的AC 方法，PPO 算法也能保持一定的优势。相比于随机分配算法，所提PPO 算法与A2C 算法分别获得了61.9%与48.8%的性能提升。

图4 车辆数量对最小速率的影响

图5给出了RIS元素数量对任务卸载情况的影响。在车辆数K=10 的情况下，随着RIS 元素数量的增加，任务卸载比例呈现上升趋势，这说明RIS元素数量的增加能够对通信质量产生积极作用，使得系统能够传输更多任务。由图5可知，所提PPO 算法的任务卸载比例最高，这说明PPO 对车载终端的服务效果最佳，有助于减小车载终端自身的计算负载。相比于均等分配，本文所提PPO算法的卸载比例提升了46.8%，A2C算法的卸载比例提升了33.2%。

图5 智能超表面元素数量对任务卸载比例的影响

4 结束语

本文提出了一种RIS 辅助VEC 的部分任务卸载方案，为车辆无法与RSU 直接通信提供了计算服务，首先分析了车辆移动性，将时延容忍约束下的最小速率最大化问题建模为马尔科夫决策过程，其次结合深度强化学习与凸优化方法，设计了基于PPO 的时段分配与任务卸载算法。仿真结果验证了所提方案在计算卸载方面的可行性与优越性，验证了RIS 作为中继在改善无线通信环境方面具有显著作用。