多旅行商模型及其应用研究综述

张硕航，郭改枝

内蒙古师范大学 计算机科学技术学院，呼和浩特010022

在科学研究和工程实践中，组合优化问题（combinatorial optimization problem，COP）无处不在，同时随着近代工业的发展，更好地求解组合优化问题能为企业和个人带来更加可观的经济效益。因此它不仅成为学术界研究热点，其发展同样受到社会各界的广泛关注。目前，在计算机网络布线、集成电路设计、交通运输、资源分配等诸多领域都存在着组合优化问题。

尽管该类问题的应用领域广泛，但在求解过程中当问题规模越来越大时，解决问题的时间成本是巨大的，加之现有的许多方法对解决这一问题都没有很好的效果，因此组合优化问题也被称为NP难问题。以旅行商问题和多旅行商问题为代表的便是一类典型的组合优化问题。本文首先以TSP（traveling salesman problem）作为切入点，通过对该单一问题的简单归纳引出了作为其泛化问题MTSP（multiple traveling salesman problem）的研究，重点关注解决多旅行商的启发式方法及应用领域两方面，通过方法与应用的结合对MTSP模型未来的研究方向进行了展望。

1 旅行商问题的产生与发展

第一个旅行商问题于1954年被Dantzig等人用线性规划解决，当时的城市规模仅有49。但是随着计算机求解速度的提高和先进算法的不断引入，目前已知成功解决TSP 的城市数量为24 978 个。可以预见的是，随着科技的不断发展，未来可以计算的TSP规模会更大，各时期求解TSP规模的典型实例如图1所示。

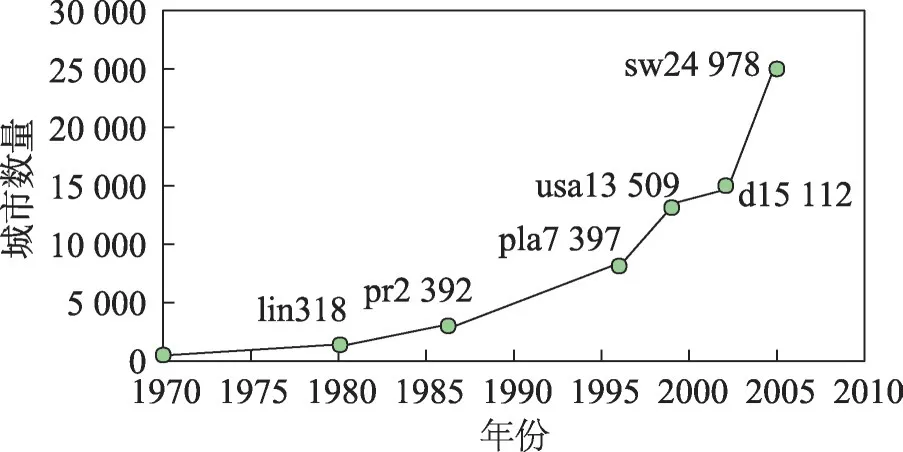
图1 TSP规模的发展历程Fig. 1 Development history of TSP scale

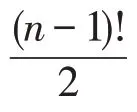
表1 TSP的计算量与计算时间Table 1 Calculation amount and calculation time of TSP

同样，线性规划作为早期解决TSP 的一种方法，主要采用的是割平面法，虽然线性规划的求解效率比穷举法高，但缺点是在求割平面时往往需要人工经验判断，这也反映出线性规划法其实并不适合解决规模较大的多旅行商问题。通过实验发现人工设计的启发式算法的一大缺陷是在不同问题集上表现不稳定，因此王原等人提出了深度学习与蚁群算法融合的框架，首先采用基于注意力机制的神经网络对问题实例进行特征提取，然后采用蚁群算法对问题实例进行求解，两种算法取长补短，通过在TSPLIB上的实例进行验证，极大改善了TSP的解。更多关于深度学习方法求解旅行商问题的其他方法可见综述文献[9]。

但经典TSP 问题是一种最基础的求最短路径规划问题，它只需要考虑路程最短这一单一条件约束，而生活中大部分实际应用问题却不能被归纳为TSP问题，例如物流配送、人员调度、巡查救援等一些涉及到多任务分配与优化的场景。多旅行商涉及到的内容更复杂，研究成果也相对较少，但是随着社会发展的需求变化，对多旅行商问题的研究逐渐成为热点。

2 多旅行商问题

作为经典组合优化问题TSP的扩展，MTSP抽象模型的研究一开始就侧重于优化旅行商的总路程，随着对该问题研究的深入以及对于实际问题的建模，研究人员发现将MTSP作为一个单目标优化问题已经不能够满足于实际需求，在路由的分配过程中，既要考虑总路程最小化，又要考虑各推销员之间的工作量的平衡；既要考虑尽可能提高公司的收益，又要考虑每个客户服务的等待时间问题。在理论模型的实际运用的过程中，优化问题往往面临多个标准的限制，具体的目标依据实际问题而不同。图2 为=3 的单仓库多旅行商问题示意图，（a）为标准多旅行商的路线规划图，（b）为考虑任务量均衡的MTSP路线规划示意图，其中0表示配送中心，1到9为城市集合。

图2 MTSP路线规划图Fig. 2 MTSP route plan

2.1 多旅行商特征

（1）销售人员类型：根据应用情况，MTSP中的旅行商可以是销售人员、车辆、机器人或无人机。

（2）销售人员的数量严格大于1，否则变为TSP问题。

（3）合作型多旅行商：几个旅行商可以合作完成给定的任务。它们可以是相同的车辆类型，也可以组合使用，例如用于卡车和无人机协同工作向客户交付包裹的交付应用。

2.2 仓库特征

（1）单仓库与多仓库

在标准MTSP中，通常只考虑一个仓库并且位置固定；而加入了多个旅行商后，多个站点的存在可以优化遍历成本。

（2）固定仓库与移动仓库

在MTSP中仓库通常是固定的，然而在某些应用中，仓库也可以是移动的。例如，移动仓库可以是无人机或卡车。

（3）封闭路径与开放路径

在经典的MTSP 中，旅行商的路径是封闭的，因为他们必须在同一仓库位置开始和结束他们的遍历。但在某些实际应用中，旅行商可以不需要返回仓库，停留在最后访问的城市即可。

2.3 多旅行商的城市规格

（1）标准MTSP：在标准MTSP 中，所有旅行商共享相同的工作空间，即他们共享所有城市。

（2）有色MTSP：有色旅行商问题（colored traveling salesman problem，CTSP）是一个广义的多旅行商问题。该问题中定义了两种类型的城市：一种是特定旅行商可以访问的单色专用城市；另一种是所有旅行商都可以访问的多色共享城市。

2.4 多旅行商的目标函数

MTSP可用于优化单个目标或多个目标，主要目标如表2，其中能量消耗和任务完成时间是高度依赖于行驶距离的。

表2 优化目标的细分Table 2 Segmentation of optimization goals

2.5 问题约束

（1）能量约束

旅行商在移动过程中会消耗能量。当旅行商是卡车等车辆时，其约束唯一取决于油量，但小型无人机或机器人等智能产品的自主性有限，当旅行商是智能产品或下文提到的传感器节点时，要考虑其续航能力等。

（2）容量约束

在任务期间旅行商可能携带包裹或数据。与能量约束相同，车辆容量的约束通常适用于小型车辆，如无人机只能承载小包裹，其数据存储器存储也可能是有限的。

（3）时间窗约束

在某些实际问题中，在任务中往往会给旅行商设定最晚到达时间或时间间隔等要求。在无线传感网等领域中，它可能对应于数据延迟。在这种情况下，对于节点数据的提取、转移和交付就提出了要求。

2.6 变体的形式化描述

正如前文中所描述，MTSP在不同应用中有不同的主体，但由于多旅行商遍历的公式会因旅行商是否起终点一致等问题而不同，因此作为考虑约束的多旅行商问题，设定个目标的集合为{,,…,T，个机器人的集合为{,,…,R}，则将四种情况下的多旅行商目标函数建模如下：

（1）单仓库闭合路径的MTSP

个推销员从同一起点出发，最终返回起点。

（2）单仓库开放路径的MTSP

在该模型中，旅行商在最后一处访问城市任务终止，不再回到起点。

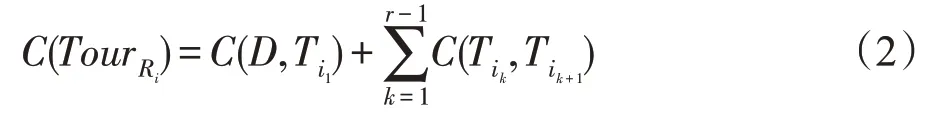
（3）多仓库闭合路径的MTSP

个推销员从不同起点出发，遍历了目标城市后最终返回到各自的起点。

（4）多仓库开放路径的MTSP

个旅行商从不同起点出发，任务结束后停留在当前城市，无须返回各自起点。

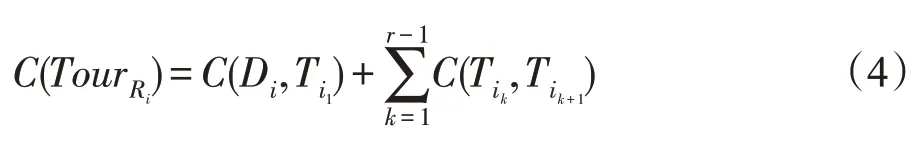
对MTSP的变体类型及主要特征的归纳如图3。

图3 MTSP的主要特征Fig. 3 Main features of MTSP

3 MTSP模型的算法求解

最初在19 世纪学者们大多采用精确算法对MTSP 进行求解，精确算法常见的包括穷举法、线性规划法和分支定界法。Ali等人用分支定界法对非对称MTSP 进行求解，求解规模最多为100 个城市；Gavish等人对分支定界法进行改进，通过限定分支定界的下界，减少了算法运行所需要的时间。该方法的关键在于如何选择合适的约束边界，不同的约束边界会形成不同的分支定界方法，因此处理多旅行商问题是不现实的。由于多旅行商问题的解空间会随问题规模的扩大呈指数方式增长，精确算法对此较难求解，而启发式算法比盲目搜索更高效，一个经过仔细设计的启发函数，往往在很快的时间内就可得到一个搜索问题的最优解，对于NP 问题，亦可在多项式时间内得到一个较优解，因此学者们逐渐倾向于采用启发式算法对MTSP 进行求解。然而随着MTSP的不断发展，从原始的优化推销员路径优化问题，到处理地面车辆和机器人调度问题，再到现在的无人机协同任务分配。变体的多样导致求解方法的侧重不同，本文将主要围绕启发式算法解决MTSP展开综述。

3.1 基于蚁群算法的方法

蚁群算法（ant colony optimization，ACO）是求解组合优化问题中一种基于种群的元启发式算法，在种群中，每个个体都是一个人工智能，可以逐渐地、随机地构造给定优化问题的解。而蚁群算法作为一大经典算法已被广泛用于路径问题中，由于其具有的极高求解效率至今仍然是学者们研究的热点问题。

Xu等人为了使多个无人水下航行器的总行驶距离最小，将该任务分配问题建模为了约束MTSP，然后提出多蚁群系统方法来求解多目标MTSP，最终使得航行器能耗最小化。文献[14]提出了面向任务的最大-最小蚁群算法，作者使用两个信息素来实现不同的目标，减轻了蚁群之间的相互纠缠来解决MTSP，目的是最小化总距离最终实现了负载平衡。Chen等人提出并实现了一种双目标问题的局部搜索方法最小化了多机器人巡逻的总行程。在该文章的实验中，与四种最经典的算法进行了评估和比较，实验结果表明该方法在求解质量方面都优于其他比较算法，但该方案比文献[16]中的模糊逻辑方法（fuzzy logic-multiple traveling salesman problem，FL-MTSP）时间更长，因为FL-MTSP 算法是先将多目标问题分解为单目标问题再提供一个最优解，在执行时间方面较有优势。Wang等人考虑了现代商业物流的时间限制和车辆的承载能力对物流优化的影响，利用改进信息素模型的蚁群算法求解了具有容量和时间窗约束的MTSP问题，提高了算法的搜索效率同时优化了最短路径。

3.2 基于遗传算法的方法

遗传算法（genetic algorithm，GA）的原理是基于自然选择和遗传，从上一代中产生最优解，但利用遗传算法求解MTSP 时，如何保持良好的个体，保持种群的多样性一直是一个难题。

文献[18]为了提高遗传算法的搜索性能，提出了两部分染色体编码方法的遗传算法来求解MTSP，实验表明该方法可以有效缩小搜索空间并优化总路程，证明了该交叉方法生成了更好的解。而叶多福等人提出了一种带复杂突变树的多染色体遗传算法，设计了一种多染色体编码的编码方式，将可行解的搜索范围大幅缩小，同时还能根据染色体数量自适应调节旅行商数量，目的是在满足时间约束的条件下，完成遍历任务且旅行商数量和旅行时间相对均衡。减少了算法运行时间，优化了旅行商数量。文献[20]提出了将选择和变异结合在一起的新的单亲遗传算法（improved partheno genetic algorithm，IPGA），通过考虑机器人的路线和染色体上的断点，使用序列编码方法来描述真实种群。将该方法与基于特定TSPLIB基准的粒子群算法（particle swarm optimization，PSO）进行了比较，IPGA 具有更好的性能。Wang 等人针对PGA 种群中个体局部信息可能缺失的缺陷，将繁殖机制集成到了入侵杂草优化算法（invasive weed optimization，IWO）中，得到了改进的带繁殖机制的单亲遗传算法（reproduction improved partheno genetic algorithm，RIPGA）。利用该改进算法研究了具有多个站点和封闭路径的多旅行推销员问题，该算法可以有效地避免局部收敛，且受参数影响小稳定性较好。胡世娟通过在杂草算法中引入繁殖机制产生后代进行遗传操作，解决了工作量平衡的MTSP，从而改善了快递员配送环节的任务平衡问题。同时，将混合局部优化算子作为变异算子加入算法中，增强了算法的局部搜索能力，实验表明旅行商数量越大，算法的优势越明显。

但是由于一些实际应用需要优化多个标准，如最小化机器人的能量消耗、任务完成时间等，用于解决MTSP的方法可能需要同时优化多个目标，这类问题被称为多目标MTSP。Bolaños等人提出了一种基于非支配排序遗传算法（non-dominated sorting genetic algorithm，NSGA-II）的多目标多旅行商问题求解方法，考虑了MTSP 的两个目标：总距离的最小化和旅行商工作时间的平衡，但作者并没有对时间的计算给出解释。文献[24]同样提出了基于NSGA-II算法的多目标优化问题，即部署无线传感器节点的多机器人轨迹优化问题。在该问题中作者考虑了三个目标：最小化任务时间（即传感器部署时间）、最小化机器人的使用数量以及平衡机器人巡视时间。

在文献[25]的研究中，作者首先将无人机作为移动sink点，其次利用遗传算法确定每架无人机对集群内每个传感器节点的访问次数。解决了大规模无线传感器网络中使用多个移动接收器进行数据收集的问题，以节省整个网络的能量并提高数据包的传输速率。而文献[26]的一项研究提出使用无人机作为信息传送节点，负责在即时延容忍网络中断开的节点之间传送信息。采用遗传算法在可行时间内求解问题。在遗传算法中构建集群的节点，使每个无人机对应一个集群，通过无人机路径的确定使得访问集群内所有节点，最小化网络中消息传递延迟。

3.3 基于粒子群算法的方法

粒子群优化算法（PSO）是最著名的元启发式算法之一，与遗传算法有许多相似之处，每次迭代中，粒子通过跟踪个体最优位置“PBest”和全局最优位置“GBest”两个极值来更新自身。

在文献[27]的研究中，作者扩展了标准PSO以处理多个目标，解决了多机器人协作任务分配问题并将其表述为MTSP，目的是使机器人的总行程和最大旅行成本最小化。在该文的实验中将提出的方法与著名的现有多目标方法进行了比较，如SPEA2（strength pareto evolutionary algorithm 2）和NSGA-II，并证明了其优越性。其中SPEA2也叫作强度帕累托进化算法，是一种相对较新的技术，用于寻找或逼近多目标优化问题的帕累托最优集。在相同的背景下，文献[30]也讨论了多机器人任务分配问题，并提出了基于动态分布式的PSO，实验部分将该分布式粒子群算法和GA进行了比较，有很强的竞争性。

3.4 其他方法

Venkatesh 等人使用人工蜂群算法（artificial bee colony，ABC）来求解单仓库的MTSP，目的是使总行驶距离（MinSum）和最大行驶距离（MinMax）最小。该作者在文献[32]中还阐述了着色MTSP，并提出了基于ABC的解决方案。关于有色MTSP的进一步研究见文献[33]，作者对ABC 算法进行了改进，引入了生成邻域解来求解MTSP。

Venkatachalam 等人提出了基于燃料约束的多无人机路由问题，通过引入两阶段随机模型来解决不确定情况下多无人机的路线规划，第一阶段目标是最小化所有无人机飞行距离的总和，而第二阶段的目标是最小化额外加油停留的预期飞行距离。实验表明采用的禁忌搜索法在中型和大型测试实例中都提供了高质量的解决方案。

3.5 基于混合算法的方法

一些研究提出了结合不同的元启发式和技术的混合算法，以更有效地解决多旅行商问题。当合作无人机在危险区域执行多个任务时，优化部署的无人机数量和每架无人机的飞行轨迹，将有助于在最短的时间内完成任务。在此背景下，Jiang 等人在研究中提出了任务分配和路径规划问题，在给定的时间约束和任务集下优化无人机的数量。为了解决这一问题，提出了一种结合遗传算法和聚类算法的协同优化算法。作者首先提出了-means 聚类算法来构建多任务的聚类，每个聚类将分配给一个无人机。其次将同一集群的相邻任务分组，以减少无人机可访问的位置数量。在考虑时间约束的情况下，基于遗传算法求解TSP 优化问题。将协同优化算法与遗传算法进行比较评价，结果表明所提出的协同优化算法比遗传算法更有效。文献[36]将蚁群算法与单亲遗传算法相结合，提出了一种新的大规模MTSP混合算法。该算法首先利用GA来确定旅行商站点的最佳值以及每个旅行商访问的城市数量，然后利用ACO计算每个旅行商的最短路径。张富震等人提出了一种基于融合粒子群-鱼群优化算法（particle swarm optimization-artificial fish swarm algorithm，PSO-AFSA）的航迹预规划任务分配策略，先对单无人机进行航迹规划模拟，再利用匈牙利算法完成各架无人机侦察任务协同分配。该算法能在优化单无人机航迹的同时，实现与任务协同分配紧耦合，使无人机集群总航程的全局总代价最低，提高了任务分配合理性。Decerle等人进一步研究解决了家庭保健问题中护理者的日程安排和路线，并将其制定为带有时间窗口的多旅行商问题。通过结合蚁群算法和记忆算法的混合方法，平衡了看护人员的工作时间。

表3将求解算法进行了分类，归纳了不同算法求解MTSP模型的最小化目标与具体解决方法的差异。

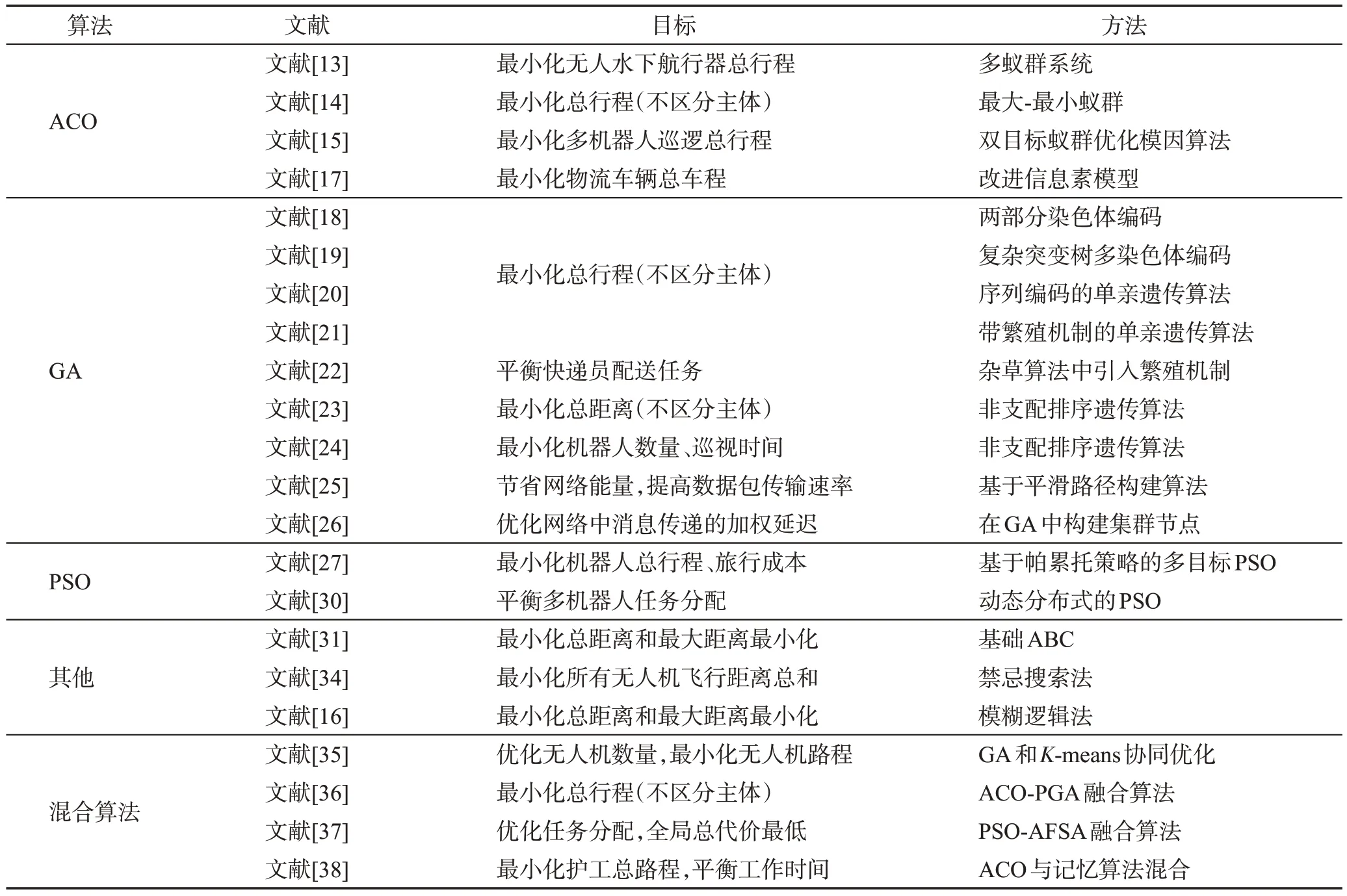
表3 不同算法下优化目标与解决方法的异同Table 3 Similarities and differences between optimization objectives and solutions under different algorithms

4 MTSP的应用领域

多年来，车辆、移动机器人和无人机作为一类可代替人工的智能手段，它们使许多复杂的任务更加安全和容易。为了实现这些任务，需要在考虑约束的同时优化给定的目标。由于MTSP 不允许重复遍历和分游等特点，该问题的解决方案可用于解决车辆路由和任务分配等路线规划的相关问题。根据应用需求，MTSP 的旅行商可以由地面车辆（机器人或货车）代表，也可以由飞行车辆（无人机）代表，而旅行商要访问的城市也可以有不同的表示，例如运输和交付服务中的客户、无线传感器网络数据收集的传感器节点、军事任务中的目标、灾害中的受困者等。本文将MTSP模型的主要应用领域分为以下五类。

4.1 物流运输与配送

在如今数字媒体和互联网+高速发展的背景下，传统物流也随之转型，逐渐成为发展国民经济中的重要一环。在服务至上的今天，既要缩短商品配送的时间，也要保证服务质量，而如何将二者兼顾，是目前的一大难题。面对运输带来的种种困难，学者们选择利用多旅行商模型来改善物流中出现的许多实际问题，使其节省成本，提高效率，来弥补运输时的不足。例如货物分发或包裹递送或汽车运输。车辆负责将货物、包裹或人员从一个地点运送到另一个地点。在这种应用中，应考虑车辆容量和时间约束。

在物流运输环节，“最后一公里”物流配送具有配送方式苛刻、配送时效要求高、个性化差异化配送需求大、订单多但规模小等特点，因而面临许多问题和挑战。但无论采用哪种配送方式，都需要解决哪个快递员、以什么顺序送达的问题，因此这类问题可以被抽象为MTSP。袁雨果以电商物流的“最后一公里”配送为研究对象，提出了解决多个快递员的任务分配和路线优化的方法，首先将该问题考虑为任务均衡的MTSP，然后设计了一种改进的遗传算法求解该问题。而文献[41]为避免多个快递员在“最后一公里”的配送任务中出现路程不均衡的现象，将此规划问题抽象成了MTSP模型，进而提出了一种新颖的回跳重组蚁群算法来优化该模型。在该目标下，不仅最小化了快递员的总配送距离，还均衡了快递员之间的配送距离。

然而随着无人机和移动机器人等新兴技术的出现，产生了新的运输服务，即利用无人机运输小包裹、移动机器人分拣快递货物等来显著缩短交付时间。如潘成浩等人针对仓储物流过程中订单拣选机器人高效的实时路径规划问题，建立了以路径总长度最小为优化数学模型的多旅行商，通过结合改进的自适应遗传算法实现批量选择路径规划，很好地适应了批量拣选机器人路径规划的需求。Murray等人同样考虑了“最后一英里”的物流交付系统，但不同之处是在该系统中，利用一辆送货卡车与一组无人机进行协同工作，相互配合，从货车上便可部署无人机的任务，使距离仓库较远的客户能够接收无人机的交付。文献[44]面对该协同任务首先最小化了卡车和无人机到达仓库的时间，其次开发了一种基于插入启发式的新算法，用来解决包含100个位置的大型问题。与传统的单一卡车或无人机交付系统相比有潜在的增益，可见成本得到了极大控制。

4.2 应急与救援

在突发事件中，应急部门需要及时、准确、有效地向受灾地区运送救援物资，最大限度地减少生命财产损失。然而大多数灾害无法提前预测，救援时间有限。因此，利用数学建模和计算机仿真技术辅助决策者在最短的时间内制定车辆调度方案具有重要的研究意义。

应急救援路径的选择主要包含疏散工作和救援物资车辆调度这两方面，其中疏散工作又包括人员疏散和车辆物资疏散。刘明等人将应急物资分配结构问题看作MTSP，并设计了一种新的混合遗传算法，优化了各种突发情况下的应急物资分配过程。在突发情况下，救灾物资的车辆调度应注重时间因素，只有及时、准确地将所需物资送达需求点，才能最大限度地减少损失。因此姚书婷等人以总配送时间最小的目标建立了一个应急物资运输的路径优化模型，同时对该模型加入时间窗约束，以此来确定最佳配送路径和时间。除了救援物资的车辆调度以外，在室内的紧急救援任务中，急救人员需要快速准确地确定被害者位置，因此需要提前制定搜索计划规划其营救路径。为了及时制定内部巡查路线，并指派救援队进行初步搜索，文献[47]将问题描述为MTSP，目标是使得每个救援队的总路径最短，缩短了搜寻时间。灾情发生后除了人员的地面搜救外，陈昕叶研究了多机器人搜索与救援的任务模式，建立了多机器人搜索和救援任务分配的组合优化数学模型。设计的算法可以满足在机器人损毁、机器人数量新增或任务新增等动态环境变化的情况下快速适应动态环境的要求。

无人机由于其航空特性和进行大规模检查的能力，在实时监测洪水、干旱和地震等自然灾害方面具有特殊优势。在完成灾情巡查、生命迹象探测等协同任务时，需要对无人机进行任务分配与航迹规划。基于上述优势，文献[49]将紧急救援和救灾中无人机的调度优化和路径优化转化为多旅行商问题，最后结合遗传算法最小化了找到目标的时间和建立通信的时间，可以高效地执行搜救任务。

4.3 数据采集与传输

近年来，无线传感器技术以及低功耗无线通信技术受到广泛的使用与发展。无线传感器由电池驱动，能量非常有限，但它们的工作时间需要几个月甚至几年。而且关键路径上的一些节点耗能过快，整个网络中的所有节点耗能不均衡，最终导致网络崩溃，网络寿命受限。因此如何降低网络能量消耗，延长网络生存时间成为无线传感网研究的热点，而优化数据传输路径则成为解决问题的一个重要途径。与传统的数据路由数据采集技术相比，无线移动节点是无线传感器网中采集数据的新技术。在无线传感器网络中，为了减少能量空洞，文献[50]通过规划移动sink点的最短路径来收集节点数据。此外，利用多个移动机器人作为移动接收器，可以帮助收集传感器节点提供的数据，这种数据收集策略使得位于固定汇聚附近的传感器节点的能量耗散最小化，从而增加了网络寿命。Huang 等人也将移动机器人引入无线传感器网络进行数据采集。针对单个机器人提出了一种最短可行路径规划算法，不仅在有障碍物的传感场中访问传感器节点，同时能最大限度地减少路径长度。这种数据收集策略允许将位于固定接收器附近的传感器节点的能量消耗降至最低，从而延长网络寿命。Wei 等人针对传感器节点的数据采集和能量充电联合问题，提出了一个多目标优化模型，提出的多目标模型优化了移动机器人的总能量效率，降低传感器节点数据传输的平均延迟。在容延迟网络中，移动机器人可以通过从源节点拾取数据并将其传送到目的节点来重新建立网络连接。

4.4 军事领域

随着人工智能时代的到来，近些年MTSP的模型还多被用于无人机等智能产品的路径规划问题中，其中，多无人机协同任务规划大致可分为系统资源分配、任务分配、导航规划、轨迹优化、武器投放规划等。

在军事任务中，集群攻击地面多目标群的研究是实现无人机群作战的重要内容。而如何在攻击地面多目标群的过程中找到最优的攻击路径是一个难题。徐国训等人根据机群攻击多目标群的研究现状，建立了机群攻击多目标群的路径规划模型，将攻击地面多目标群过程中的路径规划问题转化为MTSP问题。并提出了一种基于MTSP-GA的模型计算方法，分别得到了单基地起飞和双基地起飞的最优路径规划结果。Zhu 等人旨在研究执行打击任务的无人机的最优路径,在无人机路径规划中，考虑了时间窗和每个目标的一定环形防御范围、最佳炸弹和燃料负载等因素，以便更好地为每个无人机分配目标并确定打击顺序。将禁忌搜索算法应用于无人机航路中止和打击策略的优化，并通过数值实验验证了该算法的性能。在日益复杂的战场环境中，描述协同侦察对于与装载在不同基地的多架无人驾驶飞行器有关的空中交通至关重要。与所有无人机仅从一个基地起飞的传统问题相比，文献[55]是为了解决侦察任务，将最小逗留时间转化为最短路径组合优化问题，并将航向角离散化。将图论应用于分析路径问题，可以建立具有多种约束条件的全局模型。最后，通过遗传算法对模型进行求解，可以生成有价值的侦察路径规划。并以4 个基地的8 架无人机完成68个目标的侦察任务为例，给出了最优解，说明了所提模块化和算法的可行性和有效性。

4.5 现代农业

随着人口的增长，农作物生产的效率和产量变得愈发重要，文献[56]讨论了全覆盖条件下多收割机的路由问题，田地沿着作物方向被分成几块，目的是将多个收割机分配到田地中的各个区域，以便收获所有作物且路段不被重复遍历。该问题作为旅行商的一种延伸，不但最小化了行驶距离，还平衡了收割机间的工作量。在精准农业中，无人机可部署于农田喷洒杀虫剂。在此背景下，文献[57]研究介绍了任务分配和多架四轮直升机的路径规划问题，将其表述为MTSP的优化问题，最终成功实现了在考虑四架直升机电池容量限制的同时有效减少了任务完成时间。为了提高多臂采摘机器人在矮化、密植果园的协同工作效率，李涛等人分析了多臂采摘机器人工作时出现的访问域重叠的问题，提出了基于遗传算法的优化求解方法，既保证了各臂能避免冲突，又能在短时间内遍历所有目标果实，提高了操作效率。尽管地面车辆和无人机都对农民有很大帮助，在智慧农业系统中，采用具有多种传感器的移动机器人进行宏观信息感知也是农业可持续发展的关键步骤。因此在满足真实场景要求的区域监控策略中，优化移动机器人的行动是必要的，因此农民需要为每个机器人提供一个优化的路径，以降低成本和提高产量。Li等人提出了一种基于云的架构，由无线传感器网络、移动机器人和云系统组成，以监测温室区域。首先生成移动机器人访问的候选区域监测点，然后令机器人到达这些点的移动路径。通过对不同应用领域的分析归纳，表4将MTSP在不同变体下的分类结合适用场景进行了优劣势总结。

表4 MTSP不同变体下的分类Table 4 Classification under different variants of MTSP

5 总结与展望

本文首先对MTSP与TSP进行了辨析，以及回答了为何要着重研究MTSP 的现实意义。尽管MTSP与现实生活中的应用非常相关，但目前很多研究仍然只停留在优化数学模型的阶段，而没有考虑特定的应用领域。因此在单一旅行商问题的铺垫下，引入了多旅行商模型。由于学术研究的最终目标是要解决实际问题，本文并非是单纯地总结数学模型与改进方法，而是结合了应用领域来帮助读者拓宽研究思路。当研究是在特定的背景下进行时，如包裹递送、数据收集、监测与监控等，则伴随着MTSP变体的产生。本文在第2 章将不同应用中的变体进行了提炼总结，在不同的应用环境中考虑了不同类型的主体（车辆、机器人和无人机），以及要访问的仓库和城市的新特性，同时基于应用需求，在车辆路径问题中还考虑了车辆容量、能耗、时间窗等约束条件。第3章对求解MTSP 的算法进行了归纳，选取了当前主流研究中具有代表性的几类启发式算法以及混合算法。第4章对MTSP在现实中的应用进行了分类，在不同应用中根据主体的不同进行了归纳与概括。

（1）虽然精确的方法可以给出最优的解决方案，但由于NP-hard问题的复杂度高，它们只对非常小的实例有用。目前遗传算法、蚁群算法、人工蜂群算法和粒子群算法等启发式算法被广泛应用于求解MTSP 问题。但由于这类启发式算法普遍存在易陷入局部最优、早熟收敛、适用范围局限的缺点，目前对启发式算法理论方面的研究还处于不断发展中，新思想和新方法仍不断出现。通过分析现状，其发展方向有以下几个方面：①整理归纳分散的研究成果，建立统一的算法体系结构；②在现有的数学方法（模式定理、编码策略等）的基础上寻求新的数学工具；③开发新的混合式算法及开展现有算法改进方面的研究；④研究高效并行的或分布式优化算法。

（2）根据表3 可以看出，遗传算法在求解多旅行商问题中占据了绝对的主导地位，但分析文献后不难发现，遗传算法大部分采用的解决方案都是将MTSP转化为TSP，研究的焦点集中在如何用染色体编码表达MTSP，并且在改变染色体编码方式上对遗传算法进行改进。尽管遗传算法如此强大，但由于改进方法的局限性使得其发挥的空间愈发有限。因为启发式算法的诸多局限，近些年也有少量文献提出利用神经网络模型求解MTSP 的方法。由于神经网络是并行计算的，其计算量不随维数的增加而发生指数性“爆炸”，对于优化问题的高速计算特别有效。可以预见，随着神经网络等智能算法的深入研究，MTSP 这类NP-hard 问题可求解的规模会越来越大，例如可以利用人工神经网络模型解决物流配送环节中的复杂路线交叉和路径重复问题；利用机器学习预测物流时效性和利用深度学习解决智能体避障的路径规划问题等。

（3）通过对应用领域的细分可以看出，MTSP 模型的变体在物流行业和应急救援两方面仍然以车辆为主，如快递包裹的运输、伤员或物资的转移等传统场景中，地面车辆由于其自身不可替代的优势更适合执行该类任务，加之对于车辆的容量和成本等约束最熟悉也最容易掌握，因此利用MTSP模型解决车辆路由调度问题有极高的研究价值。

而机器人由于其具有可移动性，可将其用在WSN（wireless sensor networks）中执行数据的收集转发任务，利用MTSP模型规划多机器人的任务分配及路径规划可以有效降低网络能量消耗，延长网络寿命。同时，机器人现已可以代替人工执行重复性和高危险性的工作，在物流环节、农业自动化和搜救工作中都有贡献。无人机作为一种新兴产品以其独有的空中特性，在灾害巡查和军事领域都被广泛应用，执行巡查或是空中作战任务时利用MTSP 模型解决多目标的任务分配和路线规划是提升效率的关键。与车辆不同，不论机器人还是无人机，这类变体都对能量有着严格的限制，但目前却没有标准的能量消耗模型，因而在未来的研究中，可以建立多旅行的Benchmark 基准函数，通过能量消耗模型延长智能体的续航能力。

（4）随着工业4.0 时代的到来，智能产品对于生产系统的要求迫使新一代的工作系统必须适用柔性生产，但由于生产过程复杂，且机器人与人类的擅长点不同，很多工作单靠机器人或者人来完成结果都不理想。机器的优势在于持久性长，精确度高，而人的优势是认知能力强，能够对于突发的情况进行控制和下决策，因此在装配高精度的重型零部件时，人机协同的优势得以凸显。同时工业4.0 时代将是一个物流系统更加高效、供应链更加完善的时代，利用MTSP模型提高供应链中的运输和配送效率，是趋势也是必然。

（5）可以预见，由于变体的多样性，今后对MTSP可应用领域的探索会延伸向更多涉及路径优化或遍历次序的实际问题中。比如将无人机的路径规划应用于海上巡逻预警、设计风力发电机等新能源设备的架构布局方案、躲避障碍避免碰撞的更成熟的无人驾驶技术等。

6 结束语

多旅行商问题作为TSP问题的一类泛化问题，其相关研究已经逐步从解决单纯的数学问题进化成为解决一类问题中必不可少的一部分，也逐步迎来更多新的研究方向。同时，有关MTSP的研究一直以来都有着较大的现实意义和经济效益，备受应用者与研究者的关注。本文通过算法和领域两种角度对MTSP 模型进行了综述，除此之外，通过总结文献并分析文献展望了日后发展趋势。关于探求如何求解NP-hard问题一直以来都有各类专家学者不断探寻，MTSP作为其经典模型，更加值得深入研究来发掘其蕴含的价值。