基于事件触发控制的时滞电力系统负荷频率控制

周一辰，覃 露，李永刚，李 沙，孙佳辉，马 静，2

（1. 华北电力大学新能源电力系统国家重点实验室，河北保定 071003；2. 华北电力大学电气与电子工程学院，北京 102206）

0 引言

电力系统负荷频率控制（LFC）的基本目标是维持各区域间发电与负荷之间的平衡［1］。在二次调频控制中，区域控制偏差（ACE）信号的传输需要借助通信网络实现大数量和大范围的信息交换，但是不可避免地会带来时间延迟、数据丢包、乱序等多种通信问题，给电力系统的安全稳定运行带来新的挑战［2］。因此，在电力系统稳定性分析和控制器设计中，必须考虑通信延迟的影响。

目前，针对时滞LFC 稳定分析和控制器设计已经展开了一系列研究［3-4］。基于频域的分析方法主要在于求解特征值，但时滞项的存在加大了计算的复杂难度。另外，Pade 变换［5-6］、预测控制和时滞补偿［7］都很难保留时滞的原本特性且只能处理定常时滞的情况。基于时域分析的时滞相关Lyapunov分析方法［8］能够同时处理定常和时变时滞情况，其主要通过构建合适的泛函，对导数上限进行估计得到保守性更低的稳定性条件。文献［9］结合Lyapunov 理论和线性矩阵不等式（LMI），采用Wirtinger 积分不等式对具有采样和传输时延的LFC系统进行了稳定性分析。文献［10］运用Bessel-Legendre 不等式处理泛函导数积分项，得到了不同控制器增益下的时滞上界，有效降低了时滞系统的保守性。文献［11］提出一种基于频域直接法的延迟边际估计方法来设计控制器增益，具有良好的鲁棒控制性能。文献［12］考虑通信延迟的概率分布特性，利用凸组合技术，建立了时滞相关稳定性分析和控制器设计准则，得到基于LFC的PI控制器增益和时滞稳定上限。

基于传统周期采样的时间触发型时滞电力系统LFC 虽然简单易于实现，但是频繁的通信会造成网络拥塞，较高的数据传输要求将大量占用有限的通信和计算资源［13］。对于传输负担重和通信时间短的系统，需要设置合理的通信和控制方案来降低传输负担。实际应用中，ACE 信号的传输受到网络通信约束的影响，期望LFC 系统在保证频率控制效果的同时尽可能地减少通信次数来节约网络资源［14］。事件触发控制（ETC）［15-16］的通信间隔不再为常数，根据预定义的触发条件来决定是否传送数据，当触发条件成立时，传输控制信息，实现“按需通信”。文献［17-19］研究表明事件触发控制方案能够有效减少控制任务执行的次数，从而节省网络资源，减少通信堵塞。文献［20］在通信约束下结合事件触发规则来设计状态反馈控制器，但是需要反馈所有的状态信息。文献［21］设计了基于事件触发的输出反馈控制器，其比状态反馈更适用。因此，利用更少的通信资源实现系统控制性能，将事件触发机制和输出反馈控制器进行协同设计，具有实际应用价值。

考虑通信时滞和网络带宽资源受限对互联系统控制性能的影响，本文建立包含事件触发控制的时滞LFC动态模型；通过引入交叉项、增广变量和三次求和项来构造L-K 泛函，利用多求和不等式技术对Lyapunov 函数差分的上界进行估计，提出了时滞相关LFC系统稳定分析判据；在此基础上，采用变量替换法，推导基于事件触发通信和输出反馈的负荷频率控制器协同设计方案。

1 基于事件触发控制的时滞LFC动态模型

1.1 多区域LFC模型

本文研究的LFC所涉及的频率响应属于相对较慢的动态过程，因而往往忽略电网电压和功角等快速动态过程的影响，采用简化的低阶线性系统来表征系统在运行点附近的动态特征。

为便于公式推导，定义如下符号：RT和R-1分别表示矩阵R的转置和逆；diag｛·｝表示对角矩阵；IM和0M分别表示M阶单位矩阵和零矩阵；“*”表示矩阵中的对称项；⊥表示矩阵进行正交补运算。

多区域LFC 子区域i的系统结构如图1 所示，区域间通过联络线进行功率交换，原动机为非再热式汽轮机。图中：Δfi、ΔPmi、ΔPvi分别为子区域i的系统频率偏差、发电机机械输出功率变化量和阀门位置变化引起的功率变化量；Tti、Tgi分别为子区域i原动机和调速器的惯性时间常数；Di、Mi、Ri、βi分别为子区域i发电机阻尼系数、转动惯量、调速器的速度跌落系数和频率偏差因子；Tij为子区域i和子区域j间联络线同步系数；ΔPci和EACEi分别为子区域i控制器输出功率变化量和区域控制偏差信号；ΔPtiei为子区域i联络线上净交换功率；n为状态变量的维数。

电力系统的频率调节系统包括一次调频和二次调频2 个控制回路。当系统负荷变化ΔPd造成频率变化Δf时，反馈环节根据频率偏差产生一个作用于调节原动机的功率信号ΔPv，从而使发电机机械输出功率变化ΔPm来补偿负荷波动，进而使得系统频率恢复到允许值。

根据图1 所示的系统结构，选择合适的状态变量和输出变量，得到多区域LFC的动态模型为：

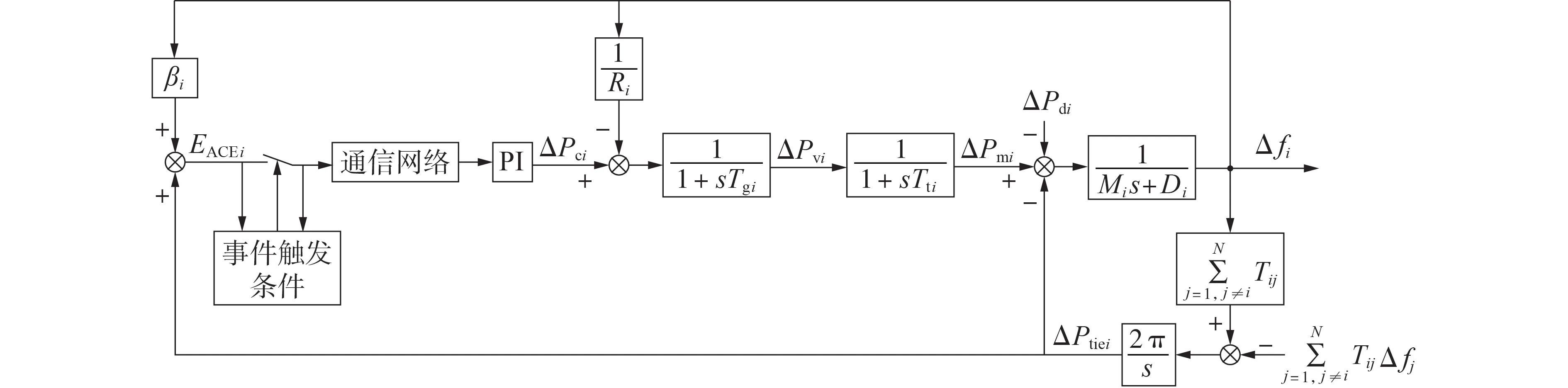
图1 基于事件触发控制的多区域LFC子区域i的系统结构Fig.1 System structure of Sub-area i in multi-area LFC based on event-triggered control

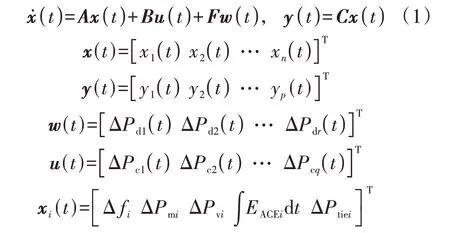
1.2 事件触发通信机制

二次调频LFC 由电网调度中心进行控制，需要借助通信网络传输ACE 信号，会引入系统时滞。为减少通信压力，本文提出基于事件触发的时滞电力系统LFC方法。事件触发器根据预定义的触发条件决定是否传送数据，当传输的控制信号ACE 满足事件触发器中设定的条件时，将传输采样信号并保存在零阶保持器中，当零阶保持器的输出值被更新时执行器才收到控制信号。此时，ACE 信号不再为周期性触发，当其变化量超过相对增量的上限时进行通信，在系统平稳运行状态下节省了大量通信资源，而在系统状态变化较大时保证了系统的必要通信。

采用输出反馈控制，输入信号u( )k可表示为：系统状态的传送由事件触发器所决定，事件触发的时刻集是系统采样的一个子集，存在如下关系：｛k0，k1，k2，…｝⊆｛0，1，2，…｝。假设成功发送x（0），事件触发的下一时刻kl+1为：

图2 为多区域LFC 中ACE 信号的采样与传输示意图。图中：τl为kl时刻事件触发器与零阶保持器之间的传输延时，且τl∈［τm，τM］，τm为时滞下界，τM为时滞上界。传感器为时间驱动型，控制器为事件驱动型，执行器端采用零阶保持器，使得控制输入信号一直保持到下一个控制输入到达执行器。传感器采样信号1、2、3、…，通过事件触发条件式（6）判断信号是否需要被传输，满足触发条件的采样信号1、4、5分别在kl、kl+1、kl+2时刻将被传输。由于通信网络存在延时τl，到达执行器端的时刻分别为kl+τl、kl+1+τl+1、kl+2+τl+2。

图2 ACE信号采样与传输示意图Fig.2 Schematic diagram of sampling and transmission of ACE signal

将时滞系统分为以下2种情况进行处理。

2 事件触发时滞LFC稳定分析

本节基于上述建立的基于事件触发控制的时滞LFC 动态模型，推导出维持闭环系统稳定的充分条件。为降低所得结果的保守性，引入多求和项、增广变量和交叉项构造Lyapunov 泛函，采用多求和不等式技术估计泛函导数上界，得到具有事件触发控制器的时滞相关LFC渐近稳定性条件。

定理1：对于给定事件触发条件0 ≤ρ＜1，如果存在正定矩阵P=［Pij］∈R5n×5n、Q1、R1∈R5n×5n、Q2、R2、R3、S1—S4、Ω∈Rn×n、对称矩阵T1∈Rn×n和矩阵Y∈R3n×3n，使得如式（14）—（16）所示的LMI成立，则系统稳定。

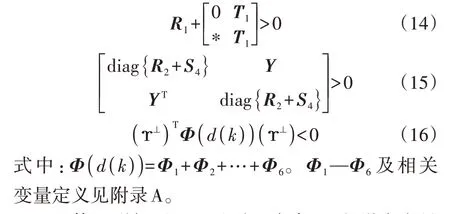
具体证明如下。通过引入多求和项、增广变量和交叉项构造L-K泛函如下：

为减少系统通信次数，结合式（6）所示的事件触发机制，得到以下结论：

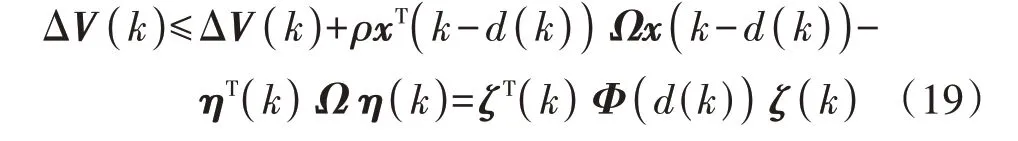
引理1及其他变量定义见附录A。

在原有L-K 泛函基础上，引入事件触发控制条件。如果满足Φ(d(k))＜0，则ΔV(k)＜0，具有事件触发条件的时滞LFC 系统稳定。基于Lyapunov 理论所提出的稳定判据能够保证系统整体的稳定性，所有模式均能维持稳定，从而保证了事件触发方案下互联多区域系统的稳定性。在此基础上，可推导得到基于事件触发控制的时滞负荷频率控制器设计判据。

3 事件触发时滞负荷频率控制器设计

本节提出基于事件触发控制的通信与输出反馈控制协同控制方案。对于控制器设计，引入非线性项导致无法直接求解控制器参数，故采用变量替换法进行解耦。

为使判据可解，首先进行如下系统线性变换处理，将输出矩阵转化为标准形式：

具体证明如下。利用Finsler 引理［23］，对式（23）进行变换可得：

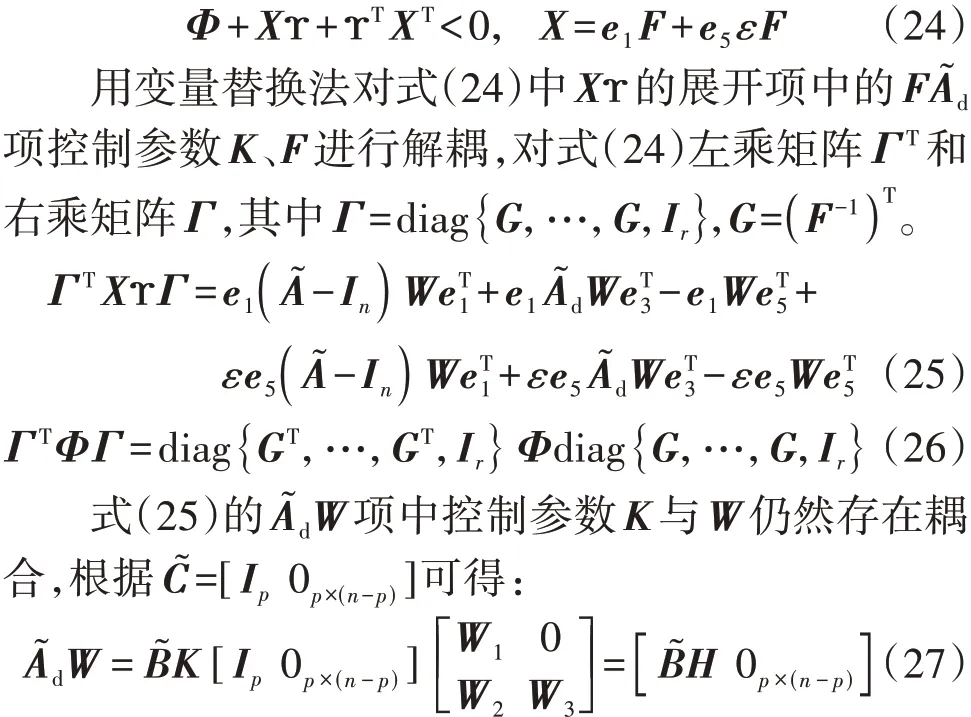
将式（25）—（27）代入式（24），即可得式（21）—（23），定理2得证。

4 算例分析

为验证本文所提方法的有效性，针对图1 所示的测试系统，利用MATLAB／Yalmip 工具箱分别求解基于事件触发控制的LFC系统时滞稳定裕度和输出反馈的负荷频率控制器增益。

4.1 时滞LFC系统稳定分析

时滞稳定裕度可用来衡量系统对时滞的容忍程度。为验证定理1 推导的基于事件触发的LFC 稳定分析判据的有效性，采用图1 所示的单区域LFC 测试系统，系统参数见附录B 表B1，设置T=0.1 s，τm=τM，然后以一定的步长不断增加τM，寻找使得系统出现不稳定的临界值即为时滞稳定裕度。根据定理1分别求解系统在不同控制参数K和事件触发参数ρ下的时滞稳定裕度如表1所示。

从表1 中可以看出，对于相同的控制器参数，触发参数ρ从0 增加到0.6 时，系统允许的时滞上限逐渐减小。这是由于触发参数越大，采样数据停留的时间越长，最终导致系统的性能恶化，从而降低了时滞稳定上限。在实际中，采用事件触发控制可以通过适当增大触发参数来降低通信成本，同时保证期望的控制性能。

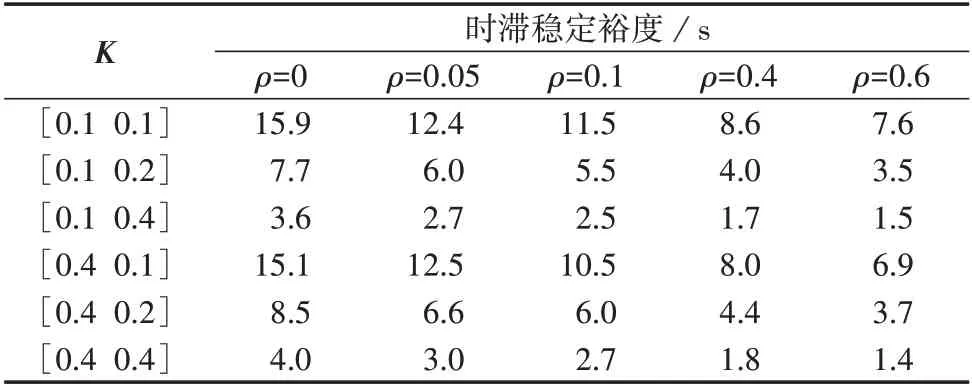
表1 不同K和ρ下的时滞稳定裕度Table 1 Time-delay stability margin under different values of K and ρ

为对比判据保守性，进一步采用文献［24］和文献［25］所提方法求解在同样的参数设置下的单区域LFC时滞稳定裕度，结果如图3所示。

图3 不同方法求得的时滞稳定裕度Fig.3 Time-delay stability margin obtained by different methods

从图3 中可以看出，不同控制器参数对应的时滞稳定裕度不同，当K=［0.4 0.1］时，采用本文所提方法求得的时滞稳定裕度相比文献［24］和文献［25］的结果分别提高了27.97%和29.73%。可见，本文所提出的时滞LFC系统稳定分析判据能够求解更大的时滞稳定裕度，具有更低的保守性。

为进一步验证定理1 所求解的时滞稳定裕度的准确性，取控制器参数K=［0.4 0.4］，触发参数ρ=0，设系统在1～1.2 s 发生0.1 p.u.的负荷扰动，得到LFC系统在不同时滞大小下的频率偏差响应曲线如图4所示，图中Δf为标幺值。

图4 中，时滞为4 s 对应系统不稳定的响应曲线，其他曲线对应系统稳定或临界稳定的响应曲线。从图4中可以看出，当时滞很小，系统在1～1.2 s出现负荷突增时，原动机快速释放动能来补偿负荷变化，频率出现跌落，经过一次调频和二次调频后，频率偏差收敛到0。当时滞增加到3.9 s 时，系统出现振荡时间明显增加，时滞继续增加到4 s 时，系统会出现发散的不稳定响应情况。时滞会降低系统的动态性能，导致系统不稳定，4 s 是单区域LFC 系统能允许的最大时滞，即系统的稳定裕度。而从表1 中也可以看出，当K=［0.4 0.4］、ρ=0 时，通过定理1 求得的时滞稳定裕度也为4 s。可见，采用定理1 能够较为准确地求解系统时滞稳定裕度，具有较低的保守性。

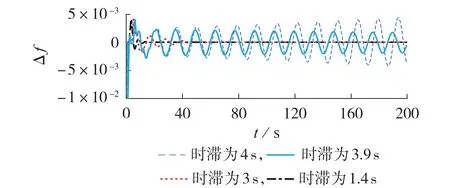
图4 系统频率偏差响应曲线Fig.4 Response curves of system frequency deviation

4.2 触发参数对数据传送率的影响

继续设置控制器参数K=［0.4 0.4］，时滞为3.5 s，触发参数ρ=0.1，当满足触发条件时系统进行通信，记为事件“1”，否则记为事件“0”。附录B 图B1 给出了事件触发结果，图5 为释放间隔与触发时间的关系图。可见不同时刻下事件触发的释放间隔不同，且大于等于采样周期。相比周期触发机制，采用事件触发控制减少了数据传输量。

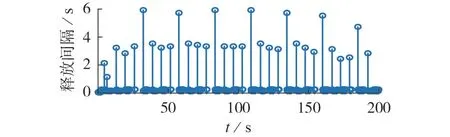
图5 事件触发释放间隔与释放时间的关系Fig.5 Relationship between release interval and event-triggered release time

数据传送率可以用来衡量事件触发的效率，定义为λk=nk/ns，其中nk和ns分别为事件触发器成功发送和接收到的数据量。事件触发阈值参数决定触发器释放信号的频率，进一步统计得到系统在不同触发参数下，触发次数和数据传送率具体情况如表2所示。从表中可以看出，当触发参数ρ=0时，对采样信号不进行筛选，任意的采样信号都通过网络进行传送，此时为周期性触发方式。当ρ=0.01，0.1，0.4时，触发事件在2000个仿真步长中分别通信了1105、640、554 次。可见随着ρ的增大，触发次数越来越少，相应数据传送率越来越小；采用事件触发控制，可有效降低信号的传输频率。

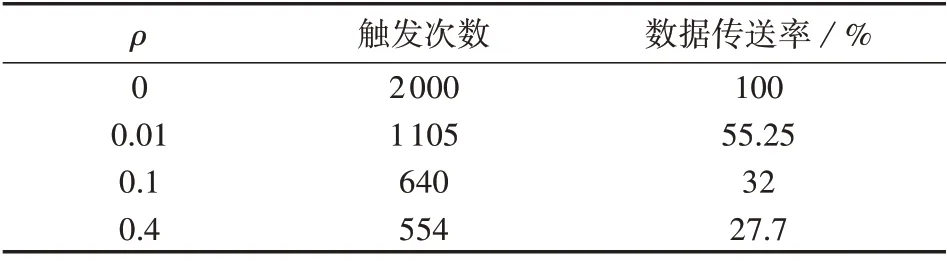
表2 不同ρ对应的触发次数和数据传送率Table 2 Number of trigger times and data transferring rate corresponding to different values of ρ

4.3 时滞LFC系统控制器设计

随着电力系统规模的不断扩大，已经形成多区域互联的大型电力系统，通信传输压力进一步增加，系统受时滞影响更加明显。为验证定理2 所提基于事件触发通信和输出反馈的负荷频率控制器协同设计方案的控制性能，假设不同区域的延迟相等，用一台等效单机模拟多机动态行为，对三区域三机互联系统进行控制器参数设计，系统参数见附录B表B2。

设置系统时滞为2 s，触发控制参数ρ=0.1，采用定理2 求解三区域互联LFC 系统的输出反馈控制增益。为对比验证本文所提控制器设计判据的有效性和优越性，选择三区域频率偏差信号、联络线功率偏差信号与时间乘积之和的绝对值积分性能指标作为目标函数，采用遗传算法GA（Genetic Algorithm）优化三区域控制器参数，并对比控制效果。设置区域1 在1～1.2 s发生0.1 p.u.的负荷扰动，系统时滞为2 s时得到的三区域互联系统频率偏差响应曲线、联络线功率偏差响应曲线分别如图6、7所示，图中Δfi(i=1，2，3)和ΔPtiei(i=1，2，3)均为标幺值。

图6 三区域频率偏差响应曲线Fig.6 Frequency deviation response curves in three regions

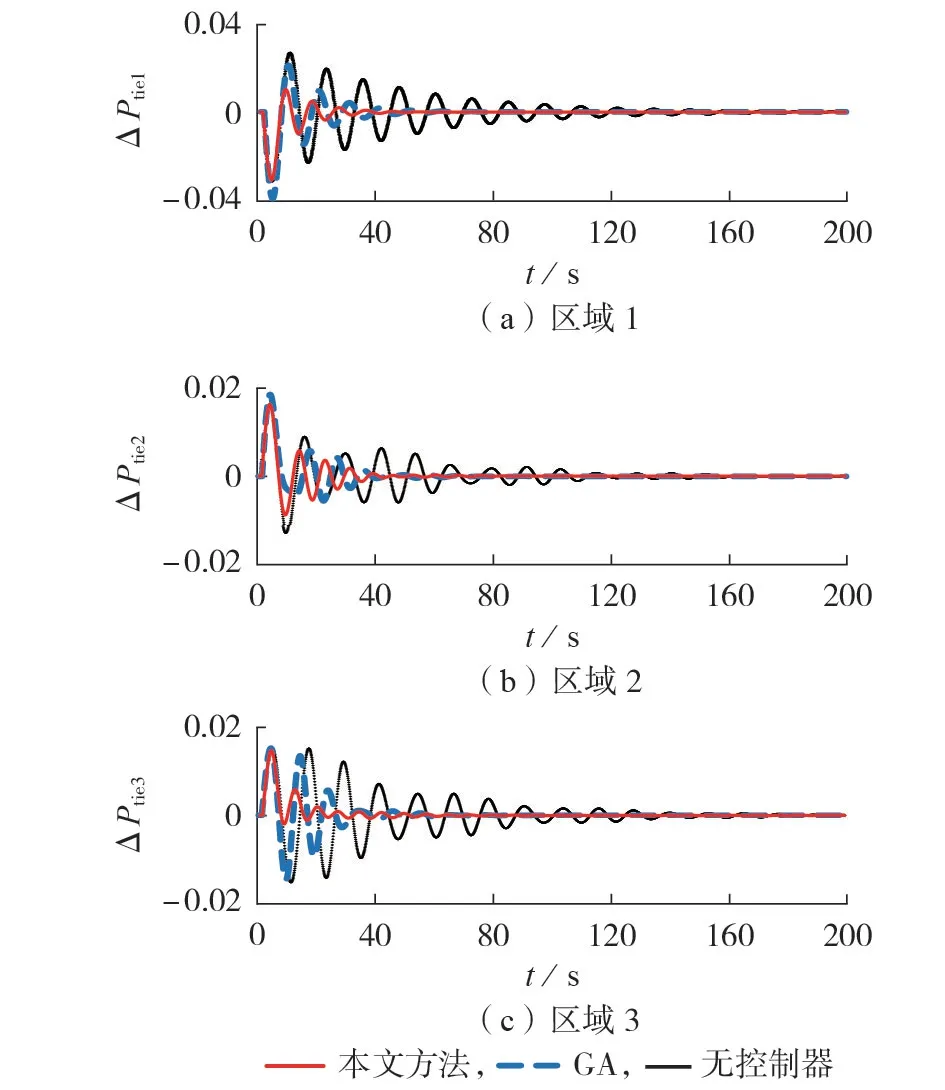
图7 三区域联络线功率偏差响应曲线Fig.7 Power deviation response curves of tie line in three areas

从图6、7 中可以看出，系统在1～1.2 s 负荷突增时，频率出现跌落，经过一次调频和二次调频后，频率偏差收敛到0。在系统时滞为2 s 的情况下，三区域频率偏差和联络线功率偏差均能在60 s左右恢复稳定。可见，相比于无控制器和采用GA 的情况，采用本文所提的基于事件触发通信和输出反馈的负荷频率控制器协同设计方案，将控制器设计问题转为LMI 的可行性问题，直接求解三区域互联LFC 系统的输出反馈控制增益，避免了优化控制中反复迭代寻优的缺陷。当系统发生扰动后，在时滞环境下能够快速消除三区域互联系统的频率振荡和联络线功率振荡，明显减小系统的振荡次数，使得偏差响应曲线快速收敛到0，从而保证系统的时滞稳定性。

进一步统计了在0～50 s 中500 个采样数据在本文所提定理2 控制方式下对应的事件触发控制释放间隔与触发时间的关系如图8 所示。从图中可以看出，采用事件触发控制，在500 个仿真步长中事件触发了259 次，数据传输率为51.8%，相比传统的时间触发控制，资源利用率明显降低。由此可见，采用定理2 所提基于事件触发通信和输出反馈的负荷频率控制器协同设计方案，在时滞环境下能够保证系统具有良好的控制性能，同时也大幅减少了系统触发通信次数，节省了通信量。

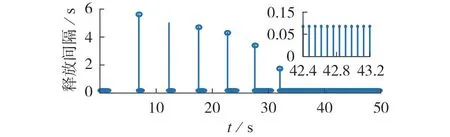
图8 区域1事件触发情况Fig.8 Event-triggered situation in Area 1

5 结论

本文考虑通信时滞和网络带宽资源受限对互联系统控制性能的影响，建立包含事件触发控制的时滞LFC动态模型。在此基础上，采用多求和不等式，提出了时滞相关LFC 系统稳定分析判据，并推导了基于事件触发和输出反馈控制的控制器协同设计方法。通过算例仿真，得到以下结论。

1）提出的时滞相关稳定分析判据定理1 可用于判别含事件触发控制的时滞LFC 系统的稳定性，在此基础上可得到不同事件触发参数下系统的时滞稳定裕度。当时滞小于稳定裕度时，随着时滞增加，系统发生扰动后频率偏差响应时间增加，但能够保持稳定，当时滞超过稳定裕度时，系统将失稳。

2）综合考虑事件触发条件、控制器增益和通信时滞的共同影响，提出了基于事件触发和输出反馈控制的控制器协同设计方案，实现了LFC 系统控制器参数设计。在时滞条件下可有效抑制系统频率和联络线功率振荡，减少振荡次数从而保证良好的控制性能。同时，也显著减少网络传输的通信量，减轻网络负担，为加强电网物理信息融合提供了新思路。

实际LFC系统受时滞不确定性等诸多因素的影响，后续将基于本文方法实现考虑事件触发条件和控制器增益的综合优化设计。

附录见本刊网络版（http：//www.epae.cn）。