水平井偏心环空中水泥浆流动特性

张新亮

(中国石化石油工程技术研究院 德州大陆架石油工程技术有限公司，山东 德州 253000)

近年来，随着水平井钻井数越来越多，水平井固井注水泥技术越来越受到重视。一般认为，水泥浆的流态为紊流时，水泥浆顶替效率较高，但对于井底存在漏层井或者循环压力很高的水平井，水泥浆不能在高泵压下紊流顶替钻井液，而且套管在环空中存在偏心的情况下会形成宽窄不一的环空间隙，这样使得顶替时不能形成稳定流态，且容易形成水泥浆和钻井液的窜槽。为此需研究水平井在低泵压和套管偏心情况下宽窄间隙处的水泥浆形成层流时的流动规律。

1 偏心环空中水泥浆流动特性

1.1 水泥浆顶替钻井液过程的基本假设

研究表明[1-7]，一般水泥浆具有明显的塑性流体流变特性，因此水泥浆采用宾汉方程进行描述。

(1)

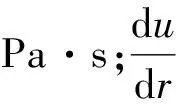
水泥浆与钻井液的顶替流动非常复杂[2]，除了他们的非牛顿性和触变性外，更主要的还在于交界面上存在极为复杂的物理、化学和力学作用。为便于实际应用和计算，工程上对顶替过程作如下假设：

(1)忽略水泥浆和钻井液在交界面处的掺混、扩散及水泥浆与钻井液不相容性所引起的化学反应等因素对顶替流动的影响。

(2)顶替过程流量恒定。

(3)水平段两端存在静水压力的作用，两端压力不等，但差别很小，故忽略此作用。

1.2 偏心环空的几何特征

对于偏心环空的流动分析[3]，引入偏心度的概念。对于内外半径分别为R1和R2的环空，内管的圆心为O1，外管的圆心为O2，其偏心距ε为两圆心距离。以内管圆心为原点，沿半径方向为射线，建立极坐标(α，r)，α变化区域为0～π，环空间隙的宽度y随转角α变化(图1)。偏心度用来表示环形空间偏心程度大小，可以被定义为

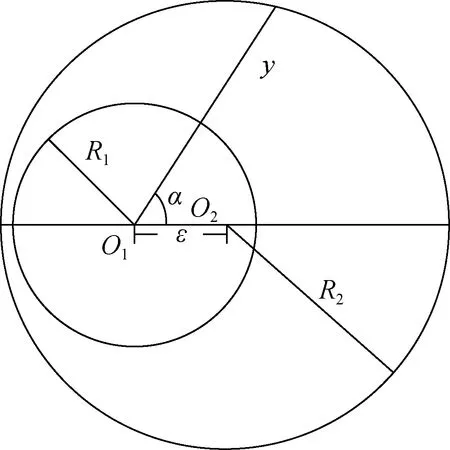
图1 偏心环空界面

(2)

式中，R1为小圆内径，mm；R2为大圆内径，mm；ε为两圆心距离，mm。

根据几何关系可得

(3)

当α=0时，环空间隙最大；当α=π时，环空间隙最小，即

y0=R2-R1+ε.

(4)

yπ=R2-R1-ε.

(5)

1.3 偏心环空液体流动基本假设

在同心环形空间四周的间隙均等，液体流动阻力在各个方向完全一样，液体流动时，环形空间的液体就会以相同的速度全部流动，不存在滞留区。在偏心环形空间内，不同间隙的阻力并不相等，间隙小的地方，阻力大，液体流动困难；间隙大的地方，液体则很容易流动。偏心环空内[1]，液体在宽间隙EE′和窄间隙CC′的流动情况，可视为液体分别在两组同心环形空间流动情况，一组由半径为R1的内管和实线圆e的外管组成；另一组则由半径为R2的内管和虚线圆m的外管组成(图2)，则偏心环形空间内不同间隙内的流量都可以分成半径不同的同心环形空间来表示。笔者把偏心环空中的流动规律通过同心环空进行研究，即把R1和R2组成的偏心环空分别以y0、yπ等一系列不同由大到小的同心环空组成。

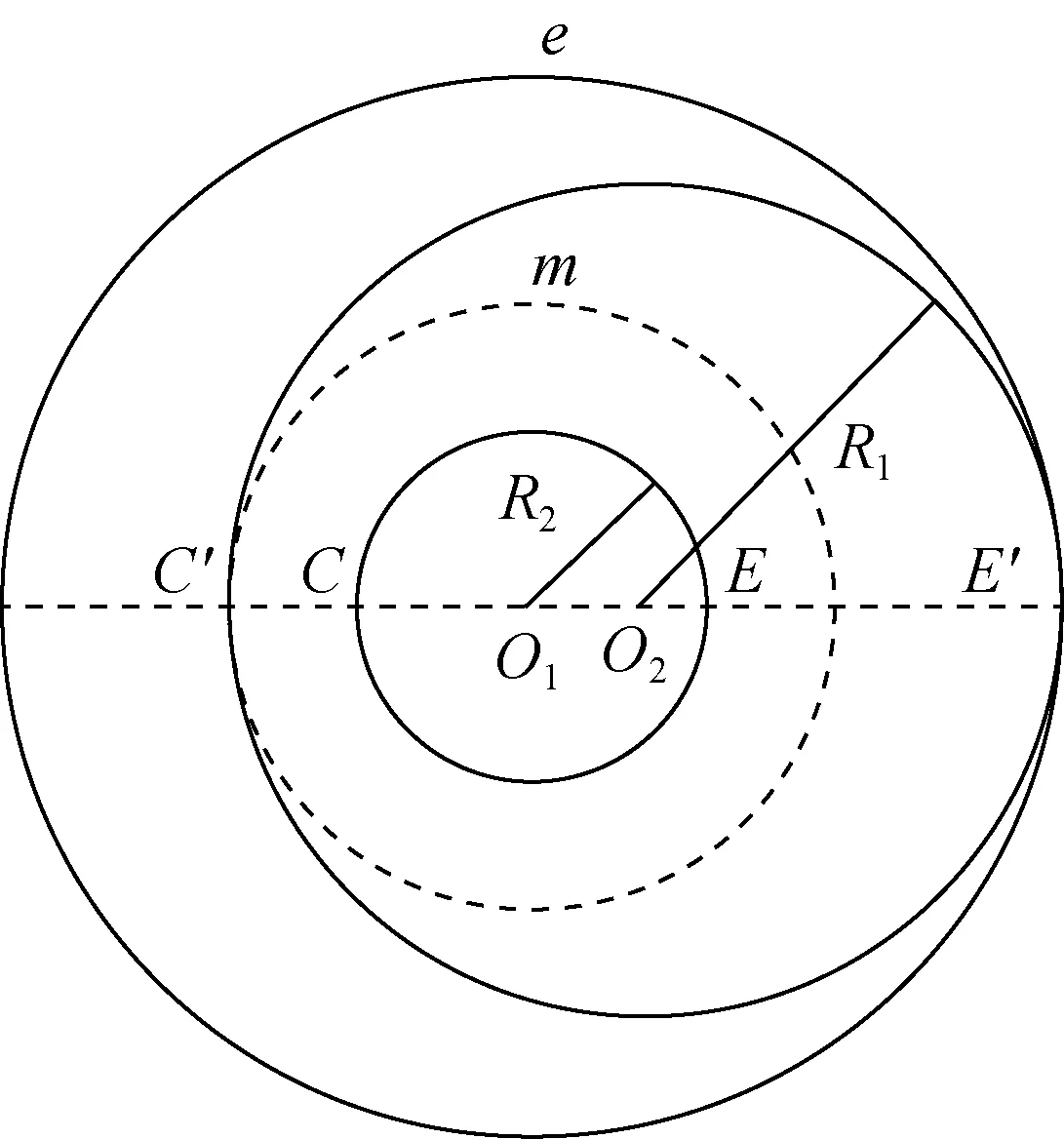
图2 偏心环空假设

1.4 同心环空层流流动计算

在同心环空中，假想在任一地方割开圆环并拉展开来，行成一个梯形截面，长边对应为环形外圆，短边对应为环空内圆，由于梯形截面上，上下边长不等，必然造成速度剖面不对称。为了简便，工程上采用一种近似方法，即假设梯形截面上速度剖面是对称的(图3)。采用这种假设带来的误差与环空间隙有关，研究表明，当环空内外径之比大于0.3时，相对误差不超过5%。

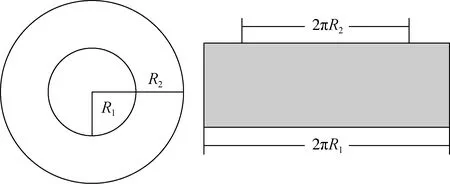
图3 同心环空假设

对于内外半径分别为R1和R2的环空，以环形空间隙中线为原点，沿径向建立r坐标[4]。在远离出入口的地方取厚度为2r、长度为L、宽度为π(R1+R2)的条形流动微元，定义流动微元为定常流动，流动微元的动量是守恒的，作用在其上的外力有：两端压力的合力2π(R1+R2)rΔP，其方向与流动方向相同，为驱动力(图4)，微元上下侧面的剪切应力τ引起的流动阻力为2Lτπ(R1+R2)。

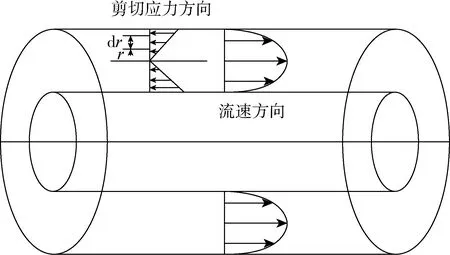
图4 同心环空层流流

由此得到动量平衡方程

(6)

式中，ΔP为环空压力，Pa；L为环空长度，m。

当r=r0时，τ=τ0，由此可得

(7)

式中，τ0为动切力，Pa；r0为流核的半径，mm。

由式(6)、(7)，可得

(8)

1.5 流动参数的计算方法

1.5.1 计算环形空间的流速

将式(6)、(7)带入式(1)，得

(9)

分离变量，整理得出

(10)

以宽间隙处为例，对式(10)进行积分，则

(11)

可得宽间隙的流速分布

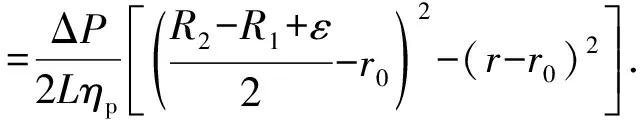
(12)

同理可得窄间隙处的流速分布为

(13)

当r=r0时，得到流核流速u0，即

(14)

1.5.2 计算环形空间的流量

整个环形空间的流量由两部分组成，设流核部分的流量为Q1，其余部分的流量为Q2，则总流量为Q=Q1+Q2。以宽间隙为例，

(15)

(16)

即宽间隙的流量

(17)

同理得窄间隙处的流量

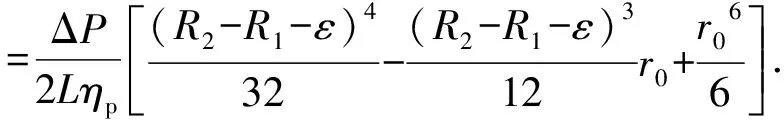
(18)

1.5.3 计算层流的断面平均流速

宽间隙处的断面平均流速

(19)

窄间隙处的断面平均流速

(20)

当流核较小时，忽略r0的高阶次。可得简式

(21)

(22)

1.5.4 宽窄间隙的雷诺数

对于非牛顿流体，引用广义的雷诺数来判断流体流态。

(23)

式中，R′е为雷诺数；ρ为水泥浆密度，kg/m3，D=R2-R1±ε，mm。

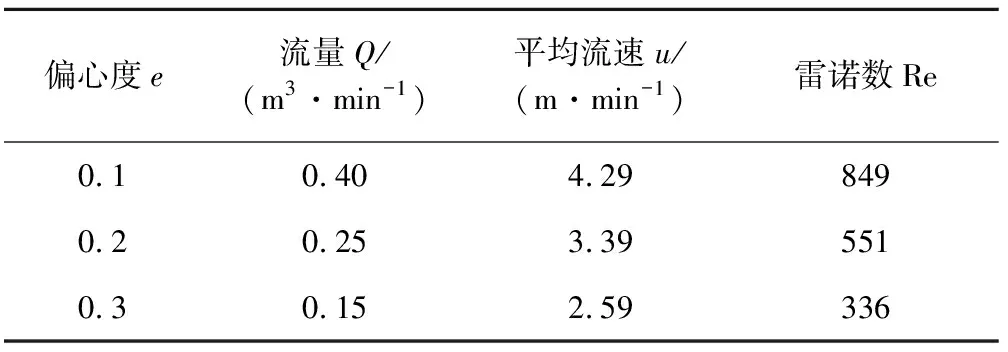
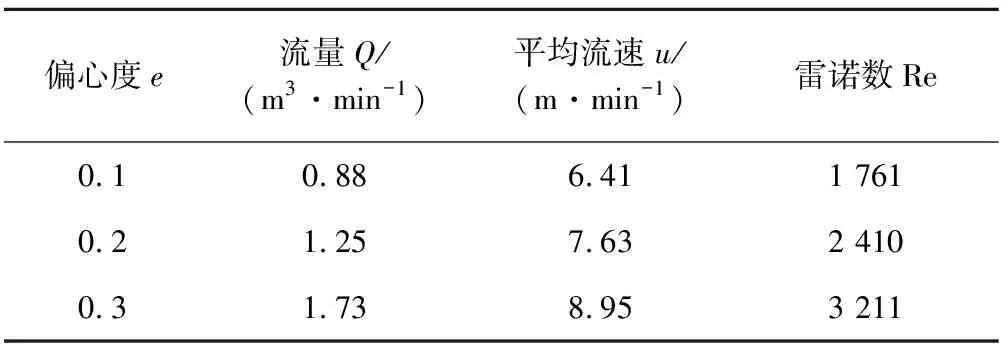
采用牛顿流体临界雷诺数Rec=2 100作为判断流体状态的标准。当R′е

2 实例计算及分析

以某口水平井固井为例，本开次钻头尺寸为215.9 mm，水平段井眼扩大率为5%，下入177.8 mm套管，井深为3 618 m，水平段长为400 m，井底存在漏层，裸眼段承压能力为10 MPa。水泥浆密度为1.9 g/cm3，流变性如表1所示。

表1 水泥浆的流变性

水泥浆一般选用转数为300 r/min和100 r/min的实测数据计算其塑性黏度和动切力，公式如下

ηp=0.001 5(R300-R100).

(24)

τ0=1.533(3R100-R300).

(25)

代入数据，计算可得ηp=0.114 Pa·s；τ0=128.77 Pa。

2.1 偏心度对偏心环空流速和流态的影响

以水平段顶替压力5 MPa计算不同套管偏心度下的平均流速和流量，以及不同间隙处的雷诺数，把已知数据代入式(17)、(18)、(21)、(22)、(23)，结果见表2、表3。

表2 不同套管偏心度窄间隙下的计算结果

表3 不同套管偏心度宽间隙下的计算结果

通过对比可以得出：

(1)当偏心度为0.1时，宽窄间隙处的流量以及流速相差较小，流态分布虽然均为层流顶替，但不同间隙处的水泥浆能稳步前进，顶替泥浆的效率较好。

(2)当偏心度达到0.2时，宽窄间隙处的流量以及流速差别较大，随着偏心度的增加，流态发生变化，窄间隙处为层流，而宽间隙为紊流。

(3)偏心度进一步增加，当达到0.3时，宽间隙处紊流趋势进一步增大，窄间隙处的顶替流速完全追不上宽间隙处的流速，极易发生窜槽。

2.2 计算层流过渡到紊流的临界泵压和流量

在Rec=2 100时计算某偏心度下宽窄间隙处形成紊流时的临界压力以及流量和流速。当偏心度为0.1时，把Rec=2 100代入式(17)、(18)、(21)、(22)、(23)，求得在宽间隙处u=7.15 m/min，Q=1.13 m3/min；窄间隙处u=4.9 m/min，Q=0.64 m3/min；临界泵压为5.7 MPa。

因此，当偏心度为0.1时，该水平井临界泵压为5.7 MPa，再加上循环阻耗2～3 MPa，当顶替压力达到7.7～8.7 MPa以上时可实现宽窄间隙均紊流顶替，且在该泵压下顶替不会造成漏失。

3 结 论

(1)套管的偏心度严重影响不同间隙处的流速分布，宽间隙处流速大于窄间隙处流速，当偏心度大到一定值甚至造成宽窄间隙处分别呈现两种顶替流态。

(2)在水平井套管偏心度大的情况下，即使泵压较小，宽间隙处的流态分布极易为紊流而窄间隙处的流态为层流，很容易造成水泥浆和泥浆的串槽，从而影响固井质量。

(3)偏心度较小时在临界压力下顶替可实现宽窄间隙皆紊流顶替且不会发生漏失。