巨厚含水松散层下开采地表移动变形规律研究

刘 辉，左建宇，苏丽娟，程 桦，朱晓峻，张鹏飞，王保国

(1.安徽大学 资源与环境工程学院，安徽 合肥 230601；2.安徽省矿山生态修复工程实验室，安徽 合肥 230601；3.安徽大学 数学科学学院，安徽 合肥 230601；4.蚌埠市勘测设计研究院，安徽 蚌埠 233040)

0 引 言

储量丰富的煤炭资源作为我国最重要的基础能源，一直占据我国能源消费总量一半以上，担负着为经济发展提供主动力的责任[1-4]。我国煤炭资源赋存状态具有一定的地域特色，东部矿区较西部矿区普遍具有煤层埋藏深、松散层厚且潜水位高等地质结构特点，其复杂的地质结构下开采地表移动变形较常规地质条件更为剧烈，主要表现为：下沉量增大、下沉系数接近甚至超过1.0、下沉盆地影响范围扩大、沉陷后易形成积水区。因此对矿区地表生态环境和群众居住生活产生了严重影响[5-8]。

针对巨厚松散层条件下开采的特殊地表移动变形规律，国内外学者从现场分析、理论分析和实验模拟等多角度对其机理进行了大量研究。研究表明巨厚松散层下开采地表移动变形的特殊性不仅仅是由上覆岩层综合岩性较软所导致的，其不可忽略的因素是煤层开采引起上覆岩层内含水层疏水渗流固结所带来的附加沉降[9-12]。对于上覆岩层内含水层疏水渗流固结引起的附加沉降，我国学者实验模拟证明了含水层失水固结机理，量化分析了含水层固结沉降量，建立了松散层底部含水层失水固结模型，取得了一定的成果[13-18]。但是以往的研究手段主要为理论分析和相似材料模拟，难以全面考虑到应力场和渗流场的耦合作用对巨厚含水松散层下开采地表移动变形的影响，从而导致结果的偏差。

以菏泽矿区某矿典型的巨厚含水松散层地质采矿条件为原型，在分析工作面实测数据的基础上，采用FLAC3D数值模拟软件，充分考虑应力场和渗流场耦合作用的影响，对巨厚含水松散层下煤层开采地表移动变形进行了流固耦合模拟，总结了采动过程中渗流固结沉降动态规律，对比分析了有无含水层情况下煤层开采地表移动变形差异，研究了松散层内含水层位置对地表移动变形的影响，为更准确预测及控制巨厚含水松散层下煤层开采引起的地表移动变形，提供一定的理论依据和技术参考。

1 研究区概况

菏泽矿区某矿位于山东省菏泽地区郓城县城南约10 km处，处于巨野煤田的中北部，其范围东起田桥断层及田桥支断层，西至煤系地层底界露头，南起3925000纬线，北至25勘探线，南北长约14 km，东西宽约11 km，地表总面积达到了222 km2。矿区地面标高+41.60～+45.38 m，浅层地下水埋深2～7 m，上覆新近系和第四系松散层平均厚度达到了590 m，局部超过700 m，属于典型的巨厚含水松散层地质条件，矿区综合柱状如图1所示。

图1 矿区综合柱状Fig.1 Stratigraphic column of mining area

通过对钻孔柱状图以及水文地质报告分析可将上覆巨厚松散层概括划分为5层含水、隔水层，见表1。巨厚松散层内第四系含水的砂层与隔水的黏土层相间沉积，属于富水性中等的松散孔隙含水层，新近系含水的砂层单层呈犬牙交错状相连，属于富水性强的松散孔隙承压含水层。

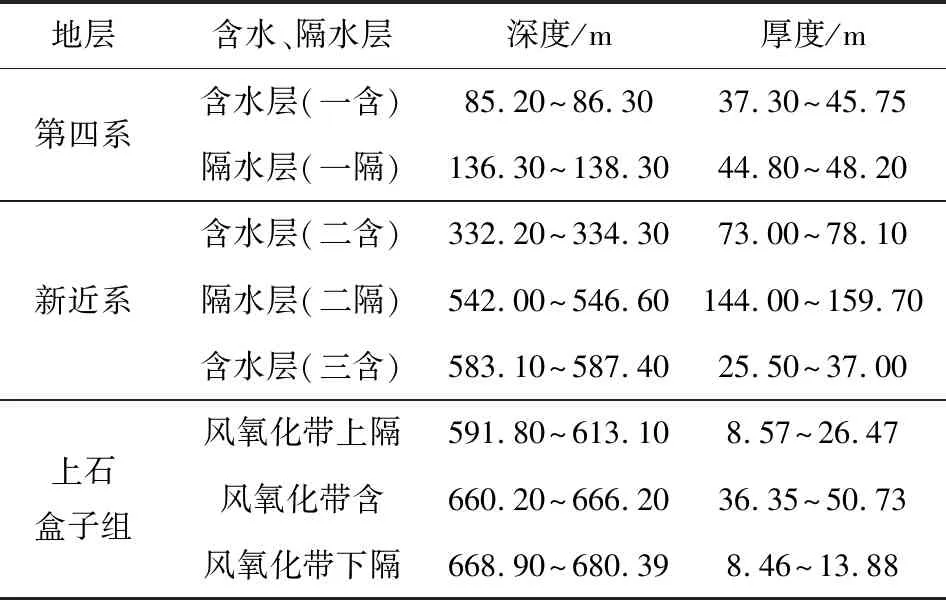
表1 矿区含水、隔水层划分Table 1 Division of aquifers and aquiclude in mining area

某矿1308工作面走向长度约630 m，倾向长度约230 m，主采煤层为山西组3煤层，煤层平均厚度为3 m，平均倾角为3°，为近水平煤层，煤层采用长壁垮落法开采，采深为765 m，工作面上覆松散层平均厚度为582 m，煤层顶板主要由粗砂岩、中细砂岩、砂质泥岩等组成，具有开采深度大、倾角小、松散层厚、松散层内含有多层含水层的特点。1308工作面移动盆地主断面上方采用十字线布设了地表移动观测线，走向观测线全长约1 550 m，累计布设47个观测点，倾向观测线全长约1 800 m，累计布设53个观测点，采动期间以平均35 d一次的频率进行观测，至停采后共观测12次。根据地表移动观测数据绘制了地表动态下沉曲线(图2)，地表移动变形参数如下：

工作面1308下沉系数q1.092水平移动系数b0.25主要影响角正切tan β1.60边界角δ056.90°

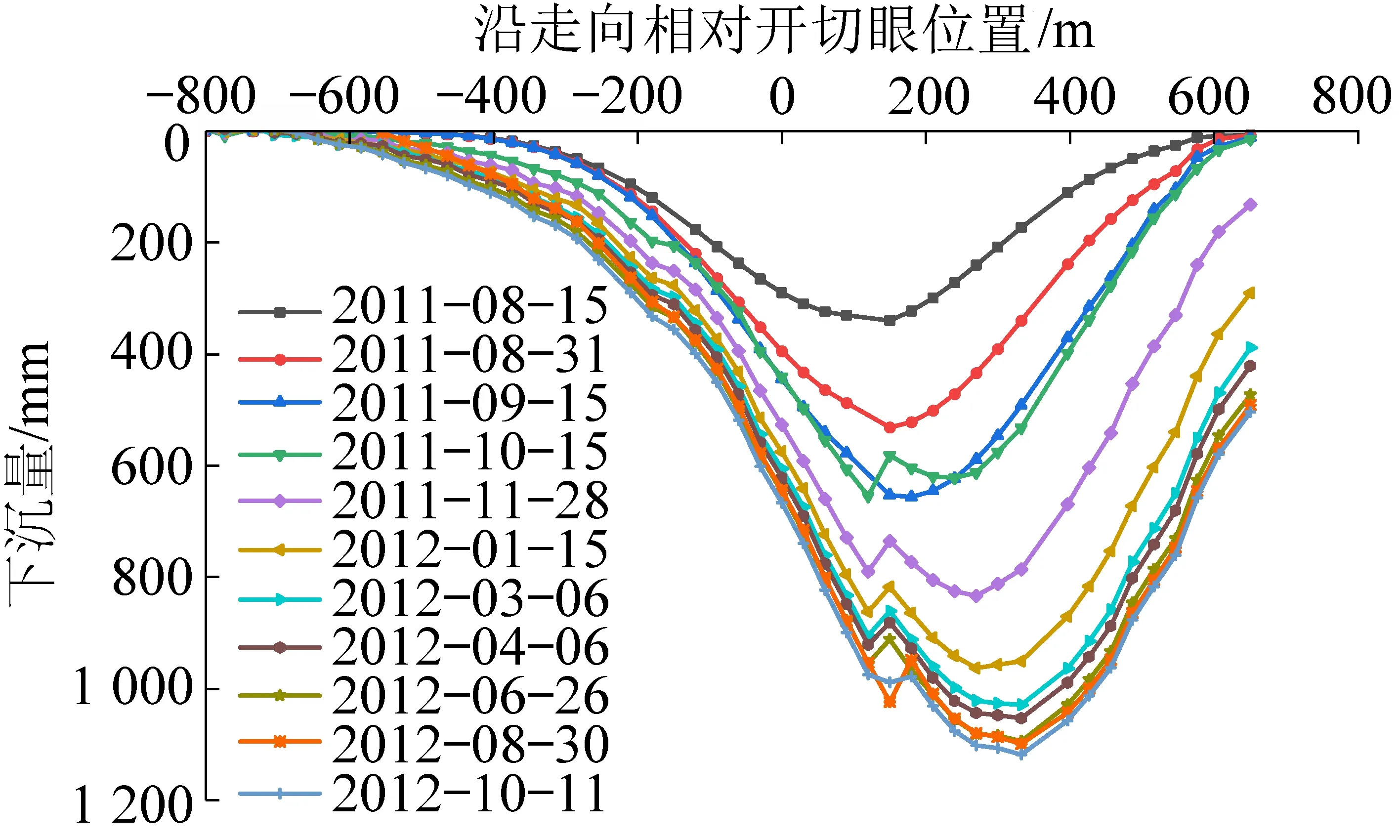
图2 工作面走向线动态下沉曲线Fig.2 Dynamic sink curve of strike line of working face

可以看出，巨厚含水松散层下开采地表移动变形与常规地质条件下采动存在一定的特殊性。相比较之下，巨厚含水松散层下开采具有移动变形初始期时间短、起动距短、初始期和活跃期下沉速度快、下沉系数大于1、主要影响角正切和边界角小、下沉盆地影响范围大、下沉盆地边界处水平位移大于下沉量且下沉盆地衰退期长、边缘收敛缓慢的特点。

2 模型设计与方案

2.1 模型设计

为研究巨厚含水松散层下开采地表移动变形规律，以菏泽矿区某矿1308工作面地质采矿条件为原型，采用FLAC3D数值模拟软件建立了模型尺寸为3 000 m×1 500 m×824 m(长×宽×高)的三维数值模拟模型。模型单元尺寸在水平方向为25 m，垂直方向按照岩层厚度不同进行合理设置。模型采高为3 m，煤层设计为水平煤层，设计的工作面长度为1 200 m，宽度为400 m，工作面沿走向方向分为12次开采，开挖步长均为100 m，开采深度为765 m，其上覆岩层内松散层厚度为582 m。为避免模型过小所导致的边界应力效应，在工作面走向和倾向两侧各留900 m和550 m的边界保护煤柱，三维数值模拟模型如图3所示。

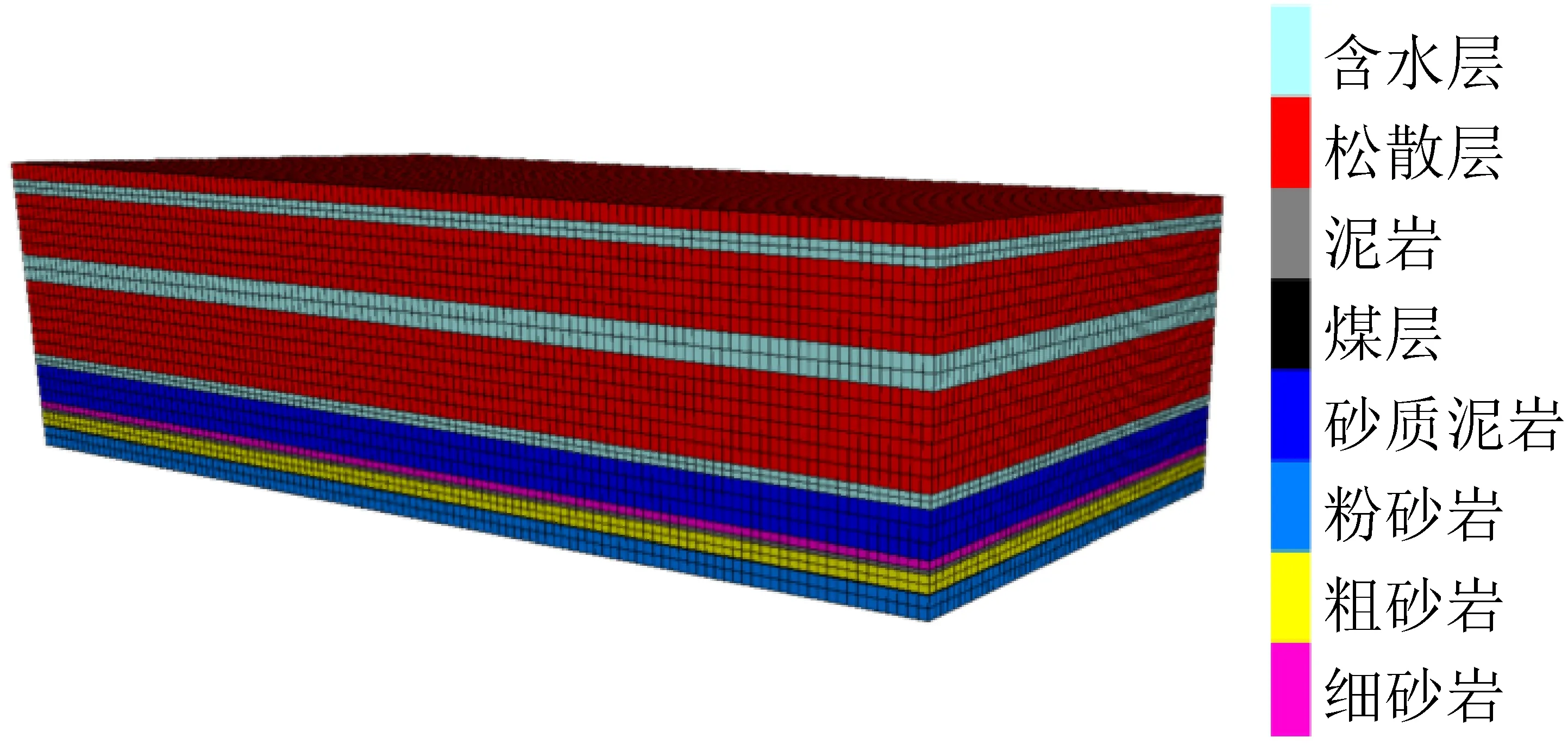
图3 数值模拟模型Fig.3 Numerical simulation model

模型的位移边界条件设置为：约束模型底面各个方向的位移，模型顶面为自由面，前后左右四面约束x、y水平方向的位移，但可以发生z方向的移动。渗流模型设置为各岩层均为各向同性且均匀等效的连续孔隙介质，力学模型采用Mohr-Coulomb屈服准则，数值模拟岩层参数根据地质资料进行概化合并见表2。

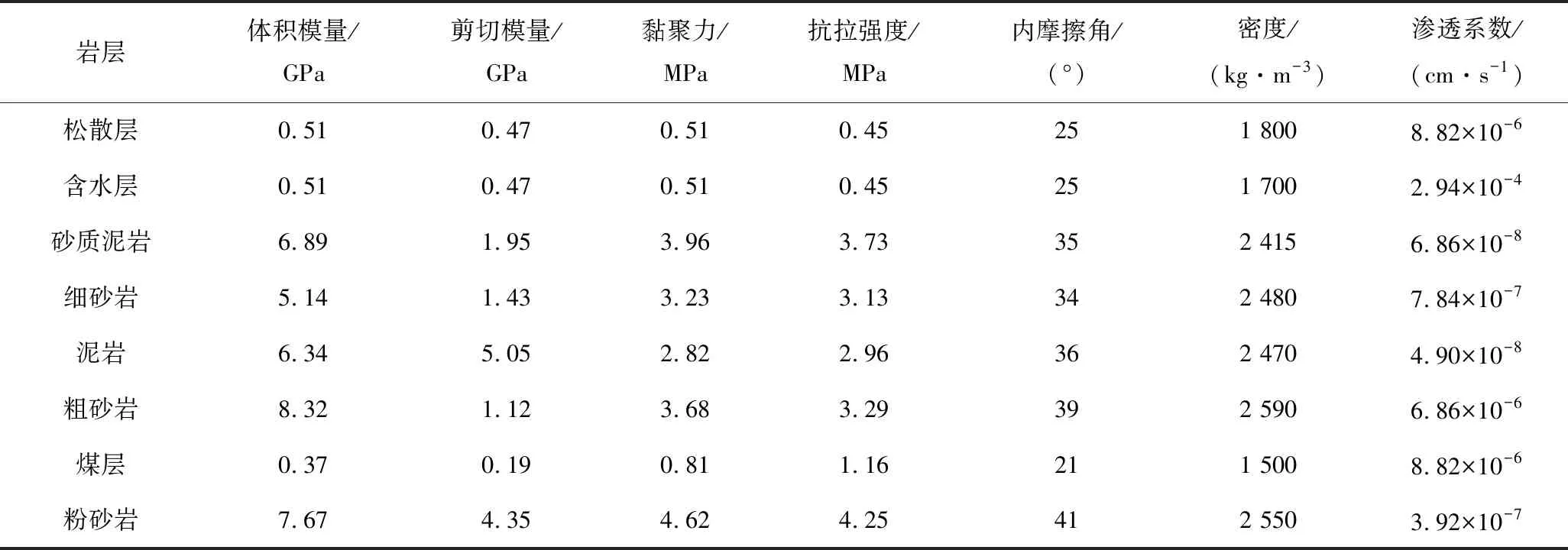
表2 数值模拟岩层参数Table 2 Numerical simulation of rock parameters

2.2 模拟方案

为研究巨厚含水松散层下开采地表移动变形规律，明确巨厚含水松散层在下沉盆地形成中的作用以及含水层位置对地表移动变形的影响，分别制定了动态固结沉降、无含水层、含水层位置3种数值模拟方案。

1)动态固结沉降方案。根据矿区含水、隔水层划分表(表1)在松散层内设置含水、隔水层，进行流固耦合模拟，研究巨厚含水松散层下采动过程中渗流固结沉降动态规律。

2)无含水层方案。不考虑巨厚含水松散层在采动中产生的流固耦合影响，进行纯力学开挖模拟，通过对比分析，研究有无含水层情况下煤层开采地表移动变形差异。

3)含水层位置方案。在松散层内设置厚度为40 m的单层含水层，通过调整含水层位置标高，分别模拟含水层底部与基岩的距离为0、100、200、300、400 m的5种情况，研究巨厚松散层内含水层位置标高对地表移动变形的影响。

3 巨厚含水松散层对下沉盆地影响

为明确巨厚含水松散层内的多层含水层在煤层开采下沉盆地形成过程中的作用及影响，对动态固结沉降方案模拟结果进行归纳总结分析，并与无含水层方案模拟结果进行对比分析，研究了巨厚含水松散层渗流固结沉降动态规律，并对比分析了有无含水层情况下煤层开采地表移动变形差异。

3.1 巨厚含水松散层渗流固结沉降动态规律

动态固结沉降方案通过循环开关流体渗流模块从而实现流固耦合模拟：在煤层开挖后，先关闭FLAC3D中的流体渗流分析模块，迭代计算至平衡，得到模型在单力学场中的土体不排水变形量(开挖变形沉降量)，然后开启流体渗流模块，流固耦合计算土体在该开挖阶段内的排水变形量(渗流固结沉降量)，流固耦合计算完成后再进行下一步开挖，并如此往复循环计算，直至工作面开挖结束。

根据FLAC3D流固耦合模拟机制，对动态固结沉降方案模拟计算结果进行分析，绘制了随工作面推进受开挖变形和渗流固结耦合作用影响的地表最大下沉发展曲线图，如图4所示。从图4可看出，当工作面推进至1 200 m开挖结束时，地表最大下沉为1.988 m，其中开挖变形沉降在地表总沉降中占主导地位，由开挖变形引起的沉降量为1.820 m，而渗流固结引起的沉降量为0.168 m，结合地表总沉降量可得出巨厚含水松散层渗流固结引起的沉降量占最终地表总沉降的8.5%。

图4 地表最大下沉发展曲线Fig.4 Maximum surface subsidence development curve

为研究巨厚含水松散层渗流固结沉降动态规律，通过计算得到了每一步开挖过程中开挖变形沉降增量和渗流固结沉降增量，并绘制了随工作面推进的地表沉降增量变化曲线，如图5所示。通过对地表沉降增量变化曲线进行分析可将开挖变形和渗流固结沉降增量的变化随工作面推进划分为同步增长期、动态变化期、同步减缓期3个阶段。

图5 地表沉降增量变化曲线Fig.5 Incremental change curve of surface subsidence

1)同步增长期。在工作面开采初期，工作面推进至200 m阶段内，开挖变形和渗流固结沉降增量呈现出同步增长的趋势，地表开始出现明显下沉，起动距约为1/4煤层埋深。

2)动态变化期。工作面推进至200～600 m，开挖变形和渗流固结沉降增量在整体上共同出现明显的增大和减小波动，其中渗流固结沉降增量随工作面推进的变化波动更为剧烈，与此同时地表出现剧烈下沉变形。

3)同步减缓期。随着工作面的继续推进至终采线1 200 m处，逐步接近走向充分采动时，开挖变形和渗流固结沉降增量呈现出同步减缓的趋势，但其整体上仍存在较小的变化波动。

3.2 地表移动变形差异对比分析

为更好地研究巨厚含水松散层的多层含水层对下沉盆地的影响，对比分析了动态固结沉降方案与无含水层方案的模拟结果，并绘制了工作面推进至1 200 m时动态固结沉降方案与无含水层方案的工作面走向下沉曲线，如图6所示。下沉曲线整体关于采空区中心对称且曲线保持连续渐变，由于工作面已推进至1 200 m，走向达到充分采动，下沉曲线底部呈现平底状，两者均符合厚松散层条件下采动引起的地表下沉曲线分布，但仍存在一定的差异性。

图6 工作面走向下沉曲线Fig.6 Strike subsidence curve of working face

通过对模拟结果进一步对比分析，得到了地表最大变形，见表3。由表3可看出：考虑松散层内含水层影响进行流固耦合计算后，动态固结沉降方案相较于无含水层方案，最大下沉值增大了0.220 m、最大倾斜增大了0.178 mm/m、最大水平移动增大了0.063 m，而最大曲率和最大水平变形分别减小了0.003 mm/m2和0.587 mm/m。

表3 地表最大变形Table 3 Numerical simulation of rock mechanics parameters

表4给出了动态固结沉降方案与无含水层方案的地表移动变形参数，通过对比分析可得：

表4 地表移动变形参数对比Table 4 Comparison table of surface movement deformation parameters

1)考虑松散层内含水层影响进行流固耦合计算后，动态固结沉降方案的下沉系数达到了1.096，相较于无含水层方案的0.974，下沉系数增大了12.5%；相比较之下，水平移动系数变化极小，动态固结沉降方案的水平移动系数仅比无含水层方案减小了1.0%。

2)对2种情况的工作面主断面走向线下沉数据分析计算可得出，动态固结沉降方案和无含水层方案的主要影响半径分别为677、641 m，相比较之下考虑含水层影响进行流固耦合计算后，主要影响半径增大了5.62%。因2种模拟计算方案的工作面平均采深不变，动态固结沉降方案的主要影响角正切比无含水层方案减小了5.28%。

3)动态固结沉降方案和无含水层方案的边界角分别为48.86°和50.22°，相比较之下动态固结沉降方案考虑含水层影响进行流固耦合计算后，边界角减小了2.71%。

综上所述，巨厚松散层内含水层受采动影响导致松散层内孔隙水压力消散，有效应力增大，产生渗流固结沉降，引发下沉盆地在开挖变形沉降的基础上再平衡[19-20]。从而导致地表下沉和水平移动变形增大，主要影响半径增大，主要影响角正切和边界角减小，下沉盆地的地表移动影响范围扩大，但最大曲率和最大水平变形的减小说明下沉盆地的整体形状在巨厚松散层内含水层疏水渗流固结沉降的作用下更为平缓[21-22]。

4 地表变形参数与含水层位置的关系

上文中对巨厚含水松散层内的多层含水层在下沉盆地形成过程中所产生的影响进行了研究，得知巨厚松散层内含水层受采动影响产生的疏水渗流固结现象会导致地表移动变形增大、地表移动影响范围扩大。为进一步探索巨厚松散层内不同位置标高的含水层对地表移动变形的影响，通过对含水层位置方案模拟数据结果进行分析，研究了地表移动变形参数与巨厚松散层内含水层位置之间的关系。

为方便表述含水层位置方案中所设置的含水层在松散层内所处的位置，定义含水层位置s为含水层底部距基岩的距离与松散层厚度的比值。

4.1 下沉系数变化规律

根据模拟结果，绘制了下沉系数q与含水层位置s之间的关系，如图7所示。

图7 下沉系数和水平移动系数与含水层位置关系Fig.7 Correlation curve of subsidence factor and displacement factor with aquifer location

从图7中可得：含水层底部与基岩之间的距离为0时，下沉系数为1.098。随着含水层底部与基岩之间距离的增加，下沉系数呈现出线性增长趋势，当含水层底部与基岩之间的距离增加至400 m时，下沉系数达到最大值1.158。对含水层底部与基岩间距为0～400 m的5种模拟结果的下沉系数与含水层位置进行相关性分析，得出下沉系数q与含水层位置s之间的相关性公式为：

q=0.087 7s+1.101 2

(1)

综上可得，下沉系数与松散层内含水层位置之间存在正线性关系。

4.2 水平移动系数变化规律

根据模拟结果，绘制了水平移动系数b与含水层位置s之间的关系图，如图7所示。

从图7中可得：5种模拟结果的水平移动系数为0.287～0.300，数值波动较小。当含水层底部与基岩之间的距离为0时，水平移动系数为0.295，随着含水层与基岩之间距离的增加，水平移动系数呈现出先增大后减小的变化规律，在含水层底部与基岩间距为200 m时达到0.300的最大值。对含水层底部与基岩间距为0～400 m的5种模拟结果的水平移动系数与含水层位置进行相关性分析，得出水平移动系数b与含水层位置s之间的相关性公式为：

b=-0.073 1s2+0.040 5s+0.293 8

(2)

综上可得，水平移动系数与松散层内含水层位置之间存在先增大后减小的二次函数关系。

4.3 主要影响角正切变化规律

根据模拟结果，绘制了主要影响角正切tanβ与含水层位置s之间的关系，如图8所示。

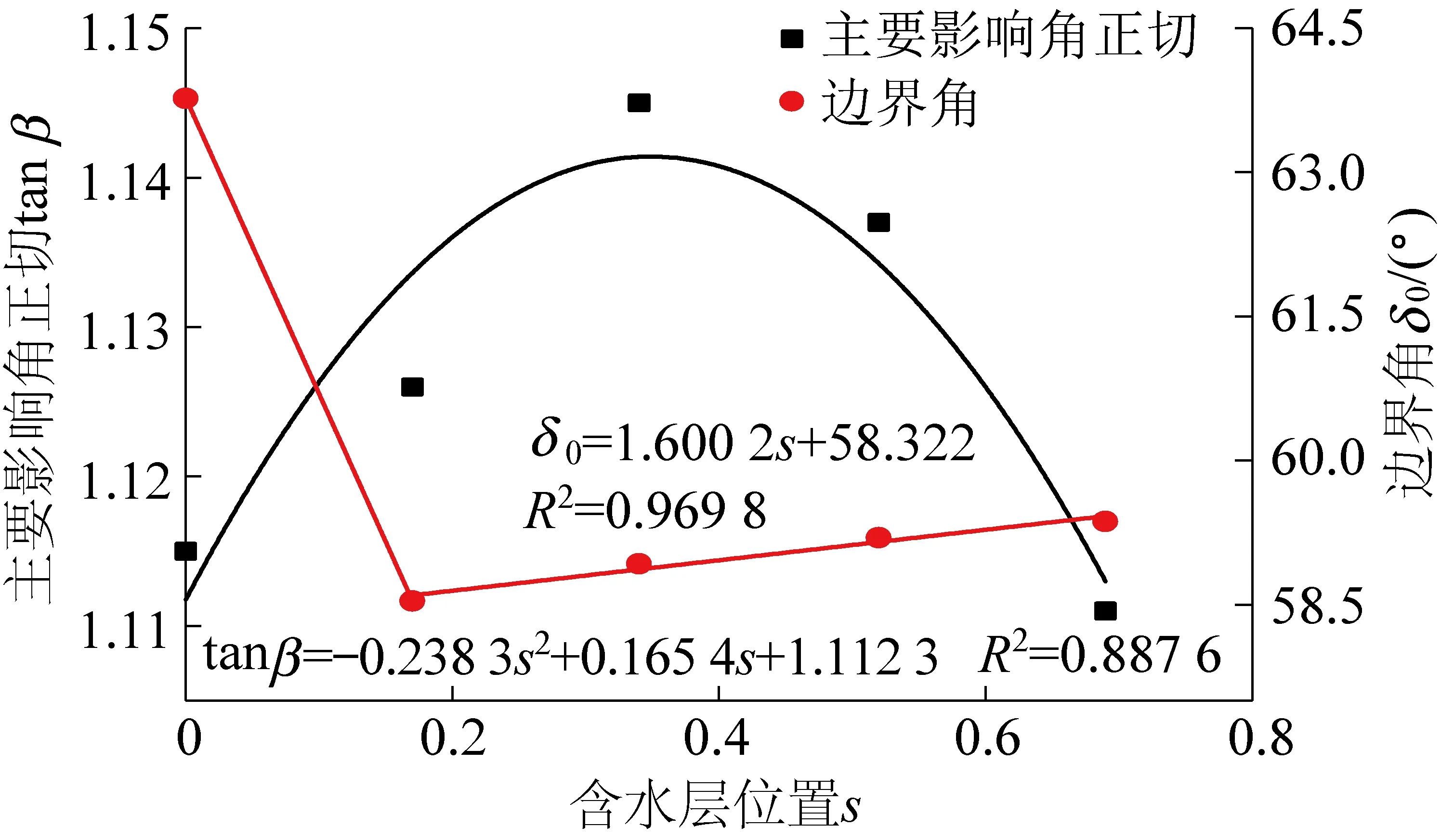
图8 主要影响角正切和边界角与含水层位置关系Fig.8 Correlation curve of tangent of major influence tan β and limit angle δ0 with aquifer location

由图8可得：含水层底部与基岩之间的距离为0时，主要影响角正切为1.115。随着含水层底部与基岩之间距离的增加，主要影响角正切呈现出先增大后减小的变化规律，在含水层底部与基岩间距为300 m时达到1.145的最大值。对含水层底部与基岩间距为0～400 m的5种模拟结果的主要影响角正切与含水层位置进行相关性分析，得出主要影响角正切tanβ与含水层位置s之间的相关性公式为：

tanβ=-0.238 3s2+0.165 4s+1.112 3

(3)

综上可得，主要影响角正切与松散层内含水层位置之间存在先增大后减小的二次函数关系。

4.4 边界角变化规律

根据模拟结果，绘制了边界角δ0与含水层位置s之间的关系图，如图8所示。

从图8可得：含水层底部与基岩之间的距离为0时，边界角为63.77°。当含水层位置与基岩不再相邻时，边界角急剧减小至58.54°，并随着含水层与基岩之间距离的增加，呈现出明显的线性增长趋势，增大至59.37°。对含水层底部与基岩间距为100～400 m的4种模拟结果的边界角与含水层位置进行相关性分析，得出边界角δ0与含水层位置s之间的相关性公式为：

δ0=1.600 2s+58.322

(4)

综上可得，边界角与松散层内含水层位置之间存在先减小后增大的关系。

5 结 论

1)某矿巨厚含水松散层采矿条件下受采动引起的渗流固结沉降占地表总下沉量的8.5%；随工作面推进，开挖变形和渗流固结沉降增量的变化可划分为同步增长期、动态变化期、同步减缓期3个阶段。

2)巨厚含水松散层采矿条件下，松散层内含水层受采动影响产生的疏水渗流固结现象会导致地表移动变形增大、地表移动影响范围扩大，但最大曲率和最大水平变形的减小说明下沉盆地的整体形状更为平缓。

3)地表变形参数与巨厚松散层内含水层位置之间存在相关性：随着松散层内含水层位置的上移，下沉系数线性增大，水平移动系数和主要影响角正切先增大后减小，而边界角先减小后增大。