MIMO-OFDM 系统的盲信噪比估计＊

洪顺利 徐建卫 李亮

1.浙江交通职业技术学院智慧交通学院；2.熵时代（北京）科技有限公司

基于对信号循环平稳特性的分析，本文提出一种MIMO-OFDM 系统的盲信噪比估计方法。首先，通过在发送端做预处理，使各发送信号循环自相关函数拥有不同的零点，将多用户问题转化成多个单输入输出的单用户问题，然后，结合发送信号循环自相关函数的能量分布规律，提出了一种信噪比估计方法。计算机仿真结果验证了本算法可以有效估计信噪比。

准确的通信信道信噪比值是反映通信质量，实现高速、高可靠性传输的重要指标。在通信信号处理的很多研究领域，功能强大的信号处理算法在运行过程中都需要将信噪比信息作为必不可少的先验信息。因此快速准确的信噪比估计算法有重要的应用。

目前的研究工作主要集中在单用户情形。信噪比估计方法分为两类：数据辅助的信噪比估计和非数据辅助的盲信噪比估计。前一种估计需要已知发送端的先验值，而盲信噪比估计方法无需知道发送信息，传输速率高而逐渐受到重视。利用OFDM 信号的循环平稳特性，已有多篇论文研究了盲信道估计及单用户环境下的盲信噪比估计。然而关于多用户MIMO-OFDM 系统的盲信噪比估计还未有相关报道。

本文提出一种MIMO-OFDM 系统中多用户环境下的盲信噪比估计方法。首先利用各个发送信号循环自相关函数拥有不同的零点，把多用户的问题转化成多个单输入输出的单用户问题；其次分析发送信号和噪声循环谱函数的能量分布规律，估计信号功率和噪声功率。计算机仿真验证了新方法的有效性。

1 系统模型

本文基于MIMO-OFDM 系统，有

M

个发射天线，

M

个接收天线，而在接收端，一个接收天线由多路信号组成，每路接收信号是由不同时延的发送信号合成的，采用多径衰落模型，则第

t

(0 ≤

t

≤

M

-1)个接收天线的接收信号可以表示为：

2 MIMO-OFDM 系统中盲信噪比估计

本文OFDM 符号块不仅引入循环前缀，使得具有循环平稳特性，同时还引入了循环后缀(CS)。其中，M表示OFDM 符号块中的数据长度；L 表示循环前缀与循环后缀的长度之和；P=M+L 表示一个OFDM 符号的长度。若在一个OFDM 符号内信道是不变的，则可以证明接收信号仍然具有循环平稳特性。

本文算法的核心是如何将MIMO 信道转化为多个单输入单输出信道。为了方便分析，以2×2 系统为例介绍多信道分离方法。

第0 个接收天线接收信号为：

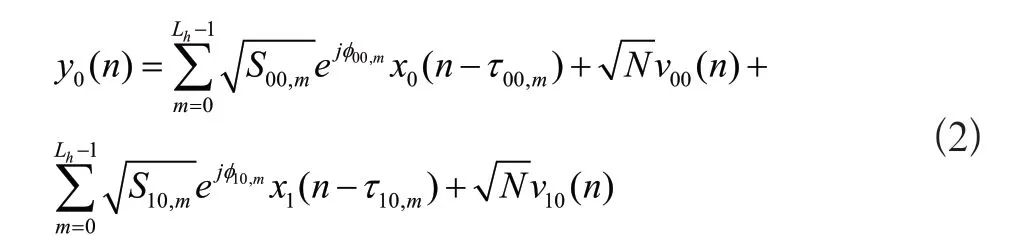
第0 个接收信号的周期自相关函数分别为：

若需要对

h

信道进行盲信噪比估计，首先，必须知道第0 个天线的接收信号自相关函数，表达式为：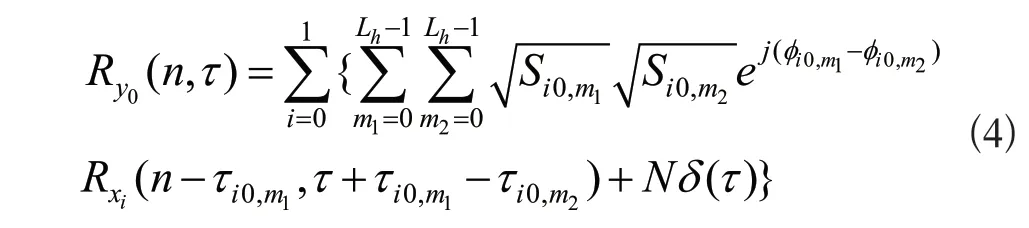

对式(4)做傅里叶变换，得到接收信号的循环自相关函数，进一步利用两径之间时间间隔相等与否，可得如下表达式：

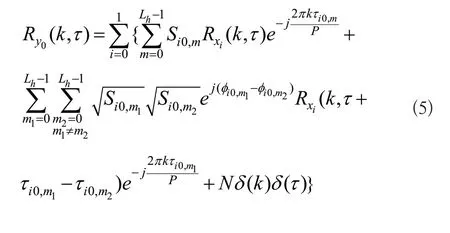
3 仿真与性能比较

本文采用2×2 系统，4QAM 调制技术；子载波数M=30；循环前缀CP=8，循环后缀CS=2，则L=10，周期P=40；而采用的信道冲击响应

h

=[1-0.8+0.2j0.6-0.3j0.8-0.5j]，

h

=[1-0.5+0.3j0.6-0.3j0.7-0.5j]，

h

=[1-0.5+0.2j0.6-0.3j0.8-0.4j]，

h

=[1-0.8+0.2j0.6-0.3j0.8-0.5j]；符号数N=1024，并进行1000 次的蒙特卡罗平均试验。如图1 所示给出了新方法的信噪比估计值与实际值随SNR 变化曲线图。新方法的

h

，

h

信道的SNR 估计值非常接近于SNR 真实值。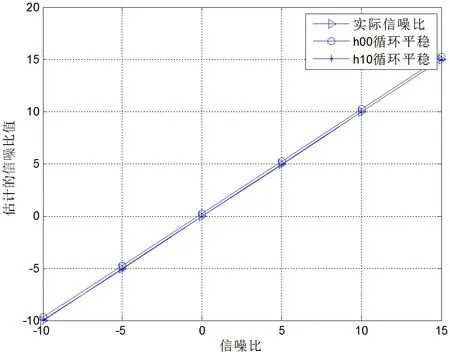

图1 信噪比估计值与实际值的比较图Fig.1 Comparison of the estimated value of SNR with the actual value

如图2 所示给出了新方法的NMSE 随SNR 的变化曲线图。由图可以看出，

h

，

h

信道的信噪比估计的NMSE 值随着SNR 变大而变小，趋势一致。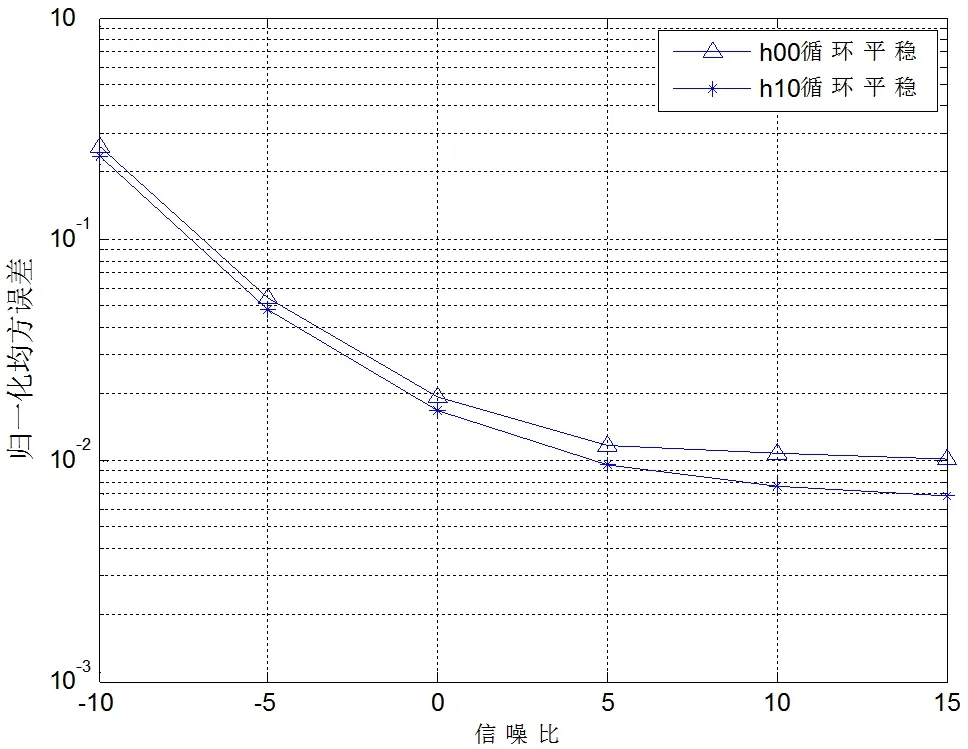

图2 新方法SNR 估计的NMSE 随SNR 变化曲线图Fig.2 The curve of NMSE with SNR estimated by the new method

如图3 所示是在不同符号数下，该信噪比估计方法的归一化均方误差值变化曲线图。

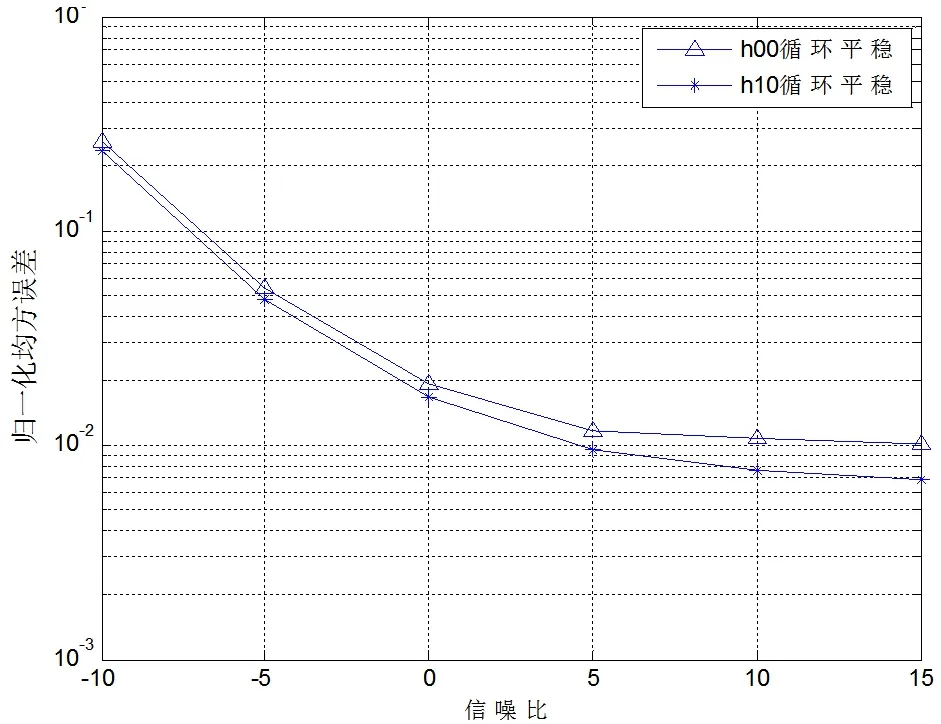
图3 新方法SNR 估计的NMSE 随符号数变化曲线图Fig.3 The curve of NMSE with the number of symbols for the SNR estimation of the new method

从仿真结果中可以看出，该盲信噪比估计方法能够有效地估计MIMO-OFDM 系统各个信道的信噪比值，且精确度较高。

4 总结

本文提出了一种基于MIMO-OFDM 系统中多径衰落信道的盲信噪比估计方法。该算法首先在发送端适当选取OFDM 信号循环后缀的长度，在接收端选取合适的循环频率，使得各发送信号循环自相关函数拥有不同的零点，达到从循环谱分布上分离信号和噪声的目的，然后利用发送信号循环平稳特性，提出一种估计信噪比的新方法。从仿真结果中可以看出该方法得出的信噪比估计值十分接近于真实信噪比值，有较高的准确性及有效性。

引用

[1] WANG J,LI B,LIU M,et al.SNR Estimation of Time-Frequency Overlapped Signals for Underlay Cognitive Radio[J].IEEE Communications Letters,2015,19(11):1925-1928.

[2] LI Y,LIU R,WANG R.A Low-Complexity SNR Estimation Algorithm Based on Frozen Bits of Polar Codes[J].IEEE Communications Letters,2016,20(12):2354-2357.

[3] TIAN J,ZHOU T,XU T,et al.Blind Estimation of Channel Order and SNR for OFDM Systems[J].IEEE Access,2018(6):126648-126656..

[4] RAZA M A,HUSSAIN A.Maximum Likelihood SNR Estimation of Hyper Cubic Signals Over Gaussian Channel[J].IEEE Communications Letters,2016,20(1):45-48.

[5] ZHANG J,ZHAO N,LIU M,et al.Blind Parameter Estimation of M-FSK Signals in the Presence of Alpha-Stable Noise[J].IEEE Transactions on Communications,2020,68(12):7647-7659.

[6] CHANG L,LI J,LI G Y.Blind Parameter Estimation of GFDM Signals over Frequency-Selective Fading Channels[C]//Signal & Information Processing.IEEE,2016.

[7] HUA M,ZHU J K,GONG M.Blind SNR Estimation Based on Cyclostationarity[J].Journal on Communications,2006,27(9):6-12.

[8] BEDI A S,AKHTAR J,RAJAWAT K,et al.BER-Optimized Precoders for OFDM Systems With Insufficient Cyclic Prefix[J].IEEE Communications Letters,2016,20(2):280-283.