水下耐压结构多部件协同优化与可靠性分析
陈俊
(上海交大海洋水下工程科学研究院有限公司,上海 200231)
耐压壳作为水下装备的主要承载结构,对其进行轻量化设计是目前大部分优化设计中的首要目标。已有的研究包括对耐压圆柱壳结构进行参数化建模,通过试验设计得到结构的响应面模型,对结构的质量和极限承载力进行优化;通过ISIGHT优化设计平台对环肋圆柱壳的模态频率等动力响应进行优化;对3种常用的近似模型进行对比分析,并采用粒子群优化算法对耐压壳进行减重设计;利用神经网络BP代理模型在MATLAB平台上对环肋锥柱结构进行优化,在最小化结构质量的同时,达到了屈曲临界应力最大化的效果。在以往的设计过程中,通过建立近似模型来完成多目标优化设计已经成为单一构件设计的重要方法之一。
多部件的结构优化需要考虑各部件的尺寸关联性,因此随机变量的选取尤为重要,需要基于主要构件的设计,建立各部件关联方程,以此为基础开展协同优化设计。优化流程见图1,设计中同时兼顾确定性的优化方法和不确定性的分析方法,分析优化结果的可靠度,并开展DFSS(design for six sigma)优化,同时保证结构强度和稳定性以及产品的质量。

图1 优化流程
1 有限元模拟与分析
某水下装备的槽型油缸结构模型见图2。

图2 结构剖面示意
该结构由上下部活塞和中部缸体3部分组成。整体结构外直径为530 mm,和分别为结构满油和空油的2种极限状态下的总长度。因特殊作业需要,满油状态下总长度需要能够容纳人员的身高,在初步设计中不能小于1 800 mm,为了方便人员的出入,后期设计中会在上部活塞的顶部开口并加设舱口盖。
1.1 模型建立
各部件的结构尺寸见图3。材料模型采用7075铝合金,密度为2.82×10kg/m,弹性模量为71 GPa,泊松比为0.33,屈服极限为503 MPa。根据潜器规范,许用应力取为0.85。为了简化分析流程,使结果更易收敛,在有限元软件中3个部件均采用壳单元进行建模,单元网格大小为5 mm。结构的设计水深为300 m,将计算载荷定为设计载荷的1.5倍,因此外压设为4.41 MPa。
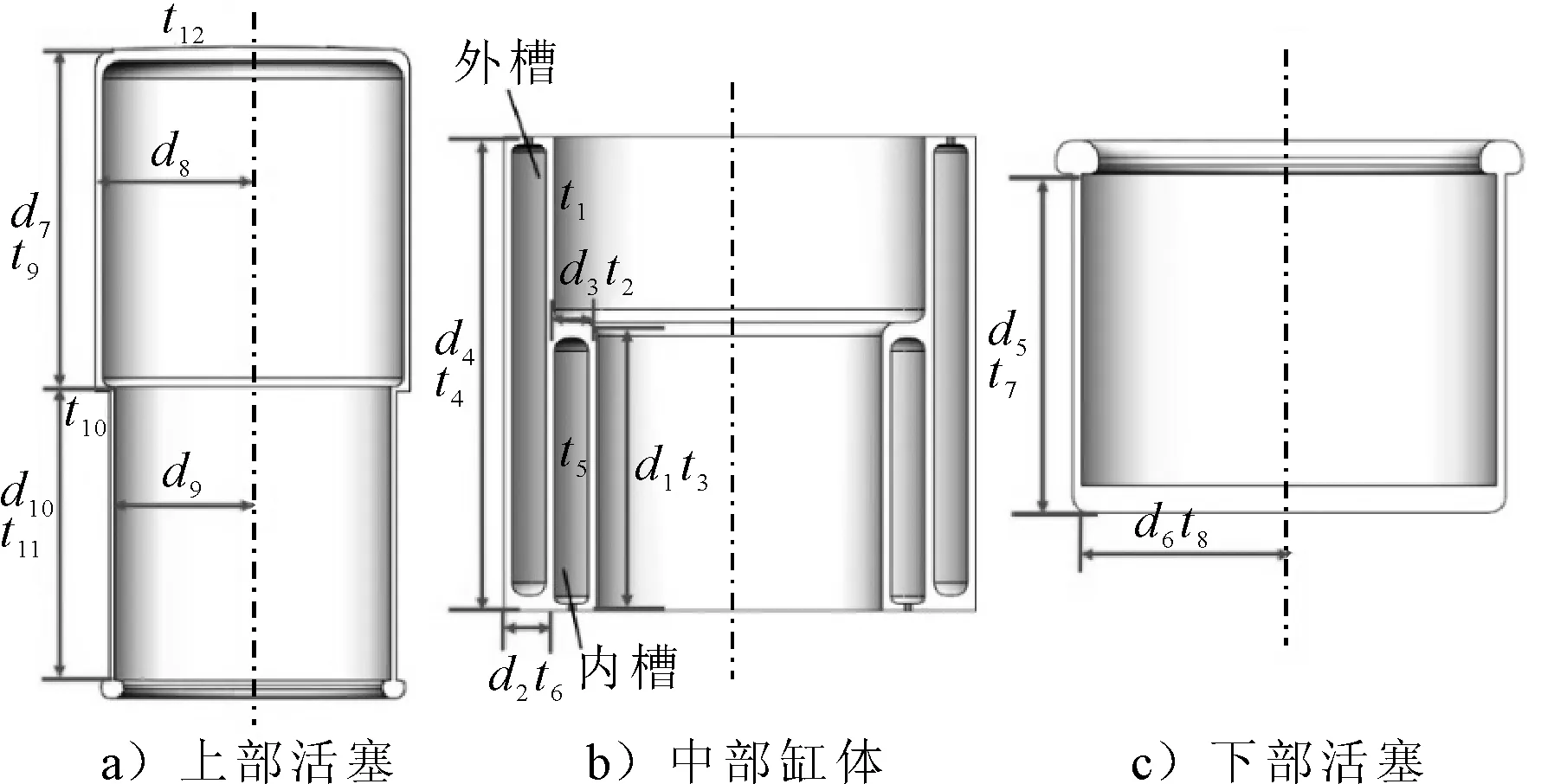
图3 各部件尺寸标注
中部缸体内的油压采用压力面积等效方法进行评估,进而分析满油状态下结构的壁面承载力。根据图3中的尺寸关系,得到内外2个槽中液压油内压力和。
1)外槽。
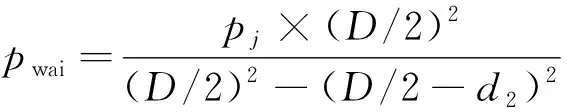
(1)
2)内槽。

(2)
式中:为外压计算载荷;为外直径;和分别为外部槽和内部槽的宽度。
1.2 数值分析结果
基于上述有限元模型,分别计算3个部件的静压强度和线性屈曲载荷,得到3个模型的应力分布图和一阶屈曲模态,见图4、5。3个部件的最大应力按图4中顺序依次为258,387,274 MPa。从屈曲模态中得到3个部件的临界屈曲载荷按图5中顺序依次为58.4,13.33 MPa,12.3 MPa,结果均远大于计算载荷,初始设计的稳定性得到保证。
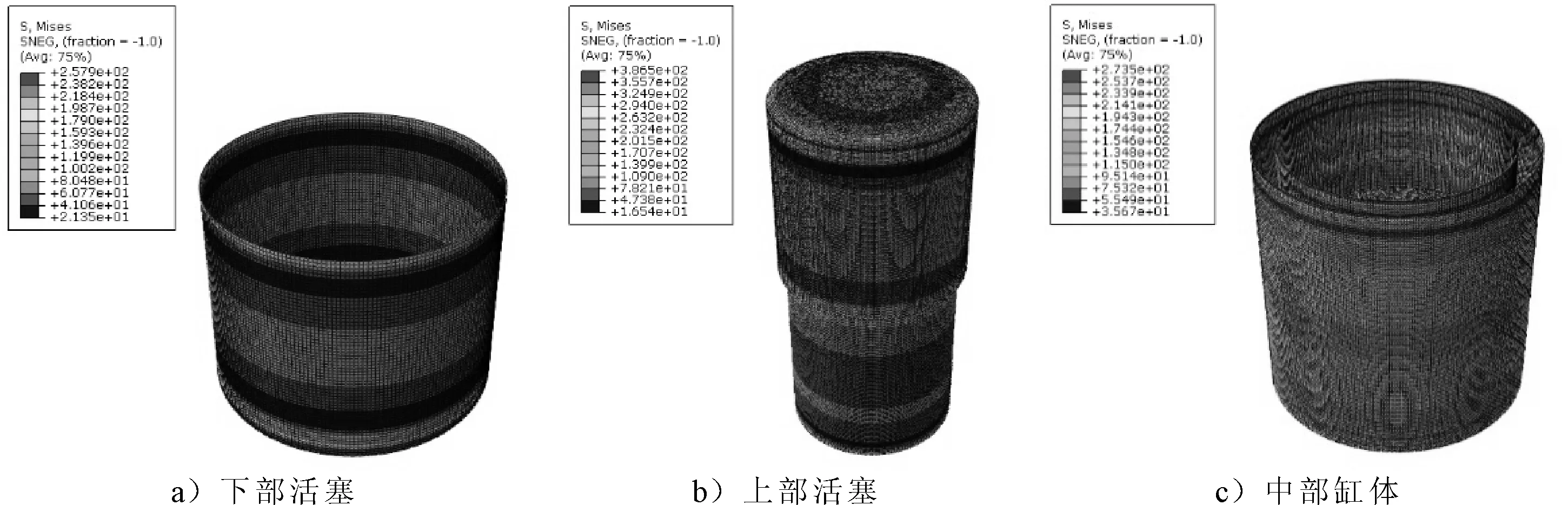
图4 各部件应力云图

图5 各部件屈曲模态
2 设计目标及要求
根据该结构设计要求,结构满油时内部高度空间需要容纳人员身高,因此满油状态下长度需尽量加长,而空油状态下长度需尽量缩短。结构在水下需满足强度和稳定性的要求,水下的重、浮力差需保证留有足够的裕度以便后续的进一步设计改造。图1中满油状态下的水平最小位置(即图3的中部缸体最小空间)大约位于人员腿部高度处,由于整体外径较小,因此该位置半径需要尽可能增大,但同时会导致内外槽内宽度的减小。由式(1)、(2)可知:随着槽宽度缩小,内部油压力会增大,壁厚也会随之增加,从而导致结构重量的增大。在优化过程中需要找到合适的槽宽以便达到空间与质量的平衡。
3 确定性多目标优化
3.1 优化数学模型
确定性优化是指将工程问题转化为数学模型,并利用相应的算法找到使设计目标达到最优时的设计点。多目标优化过程采用NSGA-II改进的非支配排序遗传算法。以中部缸体作为基础部件,共选取16个尺寸参数作为设计变量,从图3中得到设计变量及变量范围如下。
={,,…,,,,,}
(3)

式中:~为图3中3部件的板厚;为中部件内壁长度;为中部件外槽宽度;为中部件内槽宽度;为中部件外壁长度。
约束条件包括尺寸关联约束、载荷约束、应力强度和屈曲临界应力约束。载荷约束如式(1)、(2),其余约束条件如下。
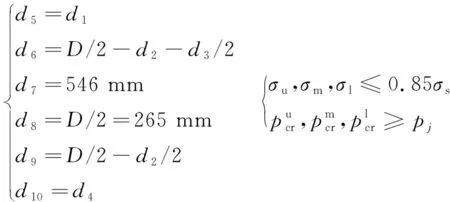
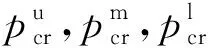
目标函数包括了上、中、下3部件的最大变形,,,满油长度,空油长度,3部件总重量,重浮力裕度和中部件腿部空间,则目标函数为
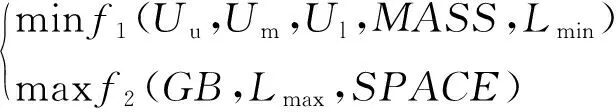
(4)
=++
=++
=+2+
=2--
=π(2)(+2+)---
π(((2)-(2-)))-
π(((2-)-(2--)))
式中:,,分别为上、中、下3部件的质量;为总体外直径;为水密度;为液压油密度;为人体质量,定为80 kg。
3.2 优化结果分析
根据优化结果对结构尺寸进行圆整处理,确定性优化的圆整值与初始设计值对比见表1。

表1 优化结果对比
根据不同目标的权重比例,重量和重、浮力差,以及腿部空间相比初始设计有较大的改善。和提升的幅度受到了的范围限制,中部件的结构变形在优化前后均小于1 mm。上、下部件的最大变形偏大,主要集中在上下2个平直圆顶板的中点处,在后续设计中会设置球形舱口盖作进一步优化。
目标函数与相关影响参数的响应面拟合曲面见图6、7。
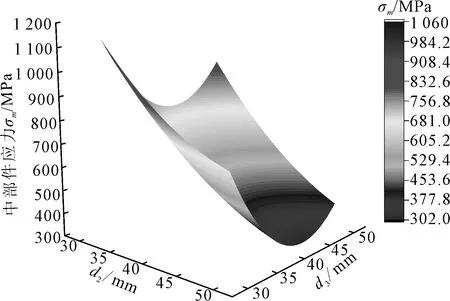
图6 中部缸体最大应力曲面
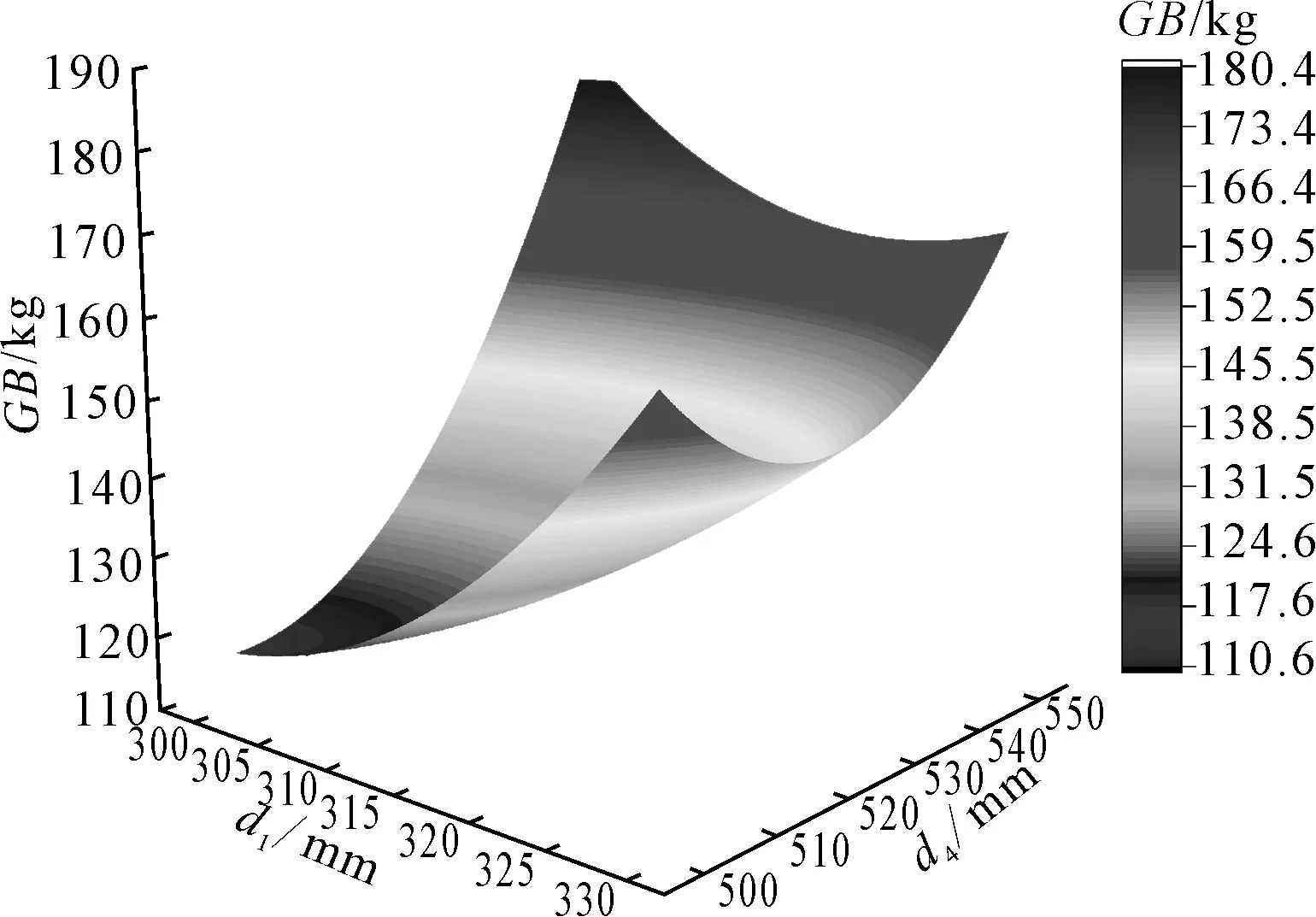
图7 重浮力差值曲面
由图6可见:中部件内外2槽空间的大小对其最大应力影响较大,外槽空间大于45 mm及内槽空间为40 mm左右时能够达到较小的应力设计点。图7所示重、浮力差值曲面中变量和的增大会导致排水量和结构质量同时增大。当达到540 mm以上时,取值范围在300 mm左右可保证最大化。
4 不确定性的可靠性优化设计
4.1 响应面数学模型
利用确定性优化的可行结果构建响应面近似模型(RSM)。拟合得到四阶多项式形如下。
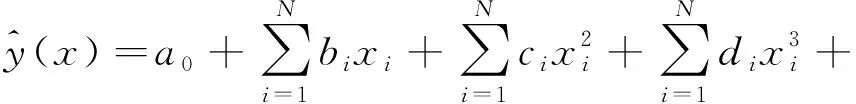
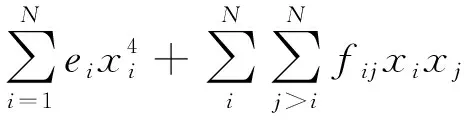
(5)
利用复相关系数作为衡量指标,误差分析发现均大于0.9,近似模型拟合效果较好。
4.2 随机变量与噪声因子
考虑结构加工误差,假设16个尺寸变量满足正态分布,均值取表1中确定性的优化解,变异系数取0.01。将材料模型和外部计算载荷的不确定性作为不可控噪声因子,弹性模量满足对数正态分布,均值为71 GPa,变异系数取0.02。外部计算载荷满足正态分布,均值为4.41 MPa,变异系数取0.05。
4.3 可靠性分析
在蒙特卡洛分析中采用描述性抽样法,共进行4 652次抽样模拟,上部件最大应力的失效概率达到2.4%,其余参数变量的可靠度均达到0.99以上。上部件最大应力概率密度见图8。3个部件的最大应力可靠度分布函数见图9。

图8 最大应力直方图
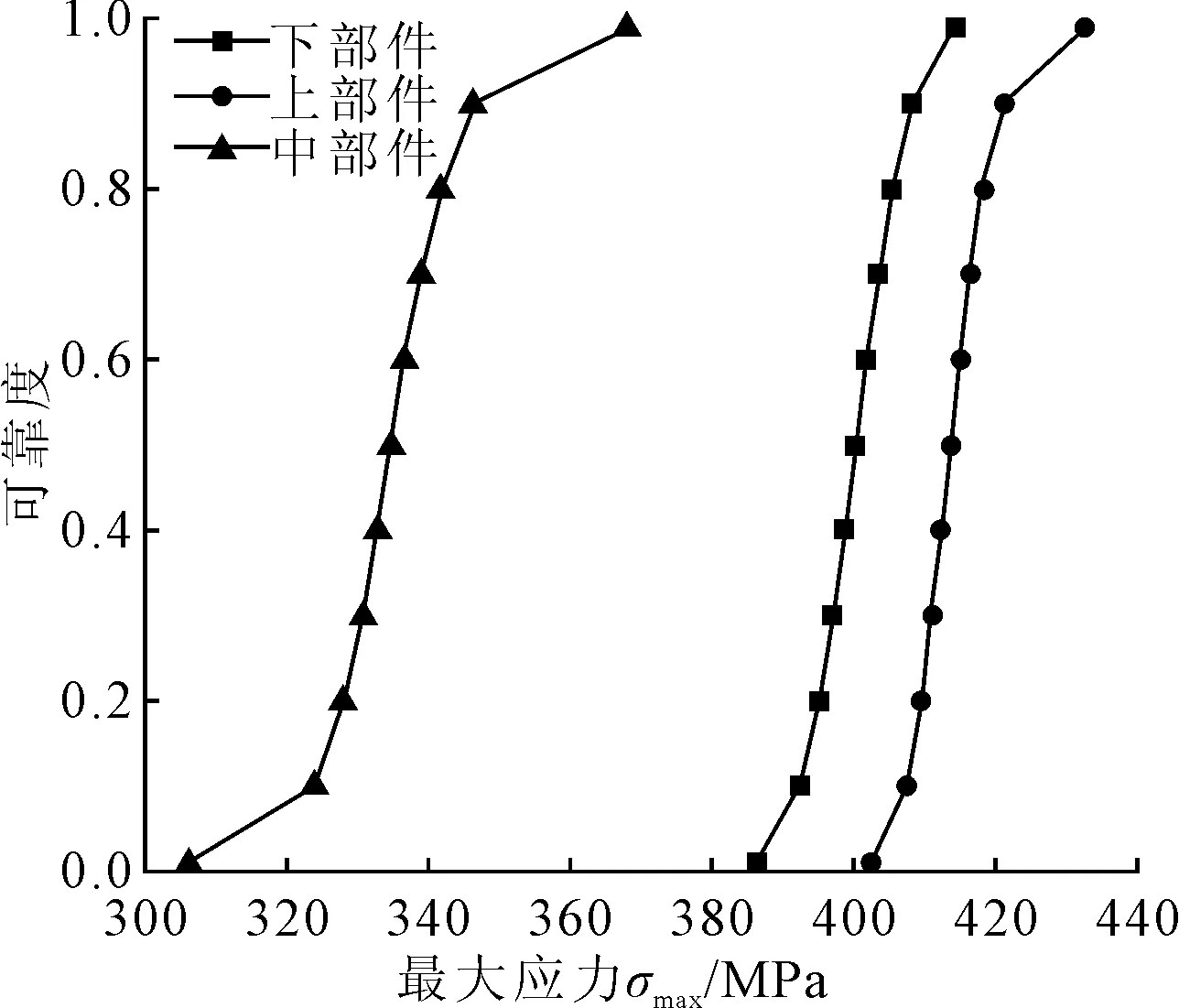
图9 可靠度分布函数图
保持随机变量和噪音因子不变,采用二阶可靠性方法(SORM)对结构进行6可靠性分析,结果见表2。6可靠性分析是利用统计学概率分析方法得到产品各项性能品质指标可靠度的分析方法。表2中得到上部件最大应力质量水平为2.41,可靠度为0.984,利用蒙特卡洛模拟得到的上部件最大应力可靠度为0.976,两种方法得到的结果相近,且都说明了上部件的失效概率略高。因此需要对结构进行可靠性优化来得到稳健性更优的设计。
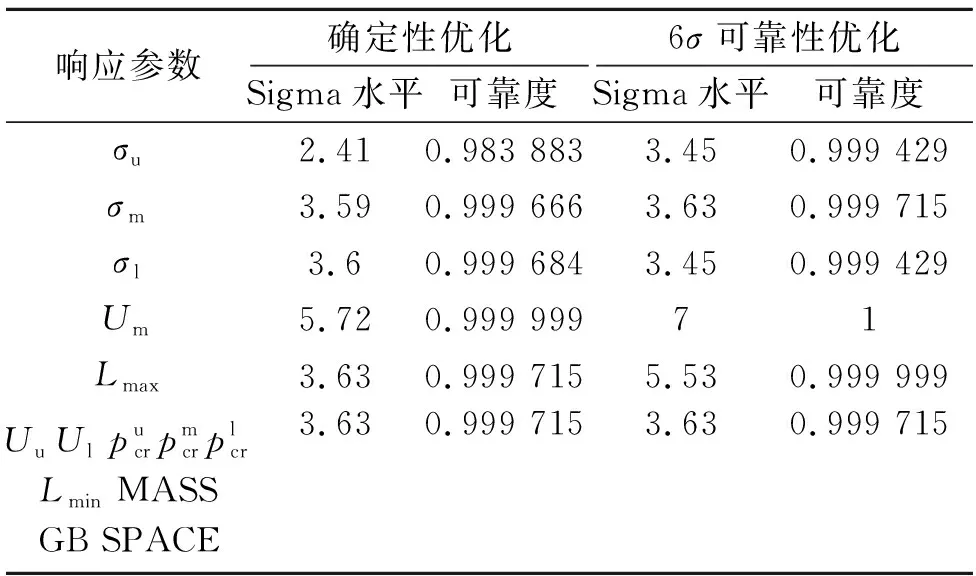
表2 可靠性分析结果
4.4 可靠性优化
通过引入噪音因子,使得设计目标既可达到最优解也可提高其可靠度。对于特制单一的产品,3水平在正态分布下的概率达到99.73%,仍然具有较高的可靠度。本设计产品属于某深海装备的特制配备,因此在工程上3水平已经可以接受。对比表2,可以看出可靠性优化后所有响应的质量水平均达到了3以上,可靠度均达到了0.999,得到了满足工程各项指标的最优解。为便于结构加工,将2次优化的结构尺寸均作圆整处理。其中屈曲临界应力在约束范围内整体减小,和在两次优化后结果相差不大,但仍有提升。权重占比最大的响应值相比初始设计有了大幅度的改善,其中总质量减少了15.3%,重浮力裕度增加了28.6%,而中部件腿部空间只增加了3%,优化效果不明显。
表1中外槽和内槽的油压力和的差值越小,中部缸体的中壁厚度会越薄,这样更有利于减轻重量。由式(1)、(2)可知:中部件外内槽宽>时,可以达到减小两槽油压差的效果,初始设计显然不满足要求。最终优化结果表明,油压差从6.48 MPa降到4.31 MPa,中壁厚度从14 mm减到6 mm,减重效果明显。
5 结论
1)在优化设计中通过拟合响应面近似模型能够可观地提高优化效率,减少优化时间。
2)基于确定性优化结果开展不确定性的可靠性分析与优化可以使得产品质量水平得到进一步提高。
3)优化目标中权重较大的结构总质量和重浮力裕度相较于初始设计均有极大的改良。而中部件腿部空间受限于油槽宽度及强度要求,因此优化效果不明显。
4)针对可靠性优化方案提出的流程体系,可为产品结构的初步设计提供参考。

