沉管管节旁拖顶推时螺旋桨推力折损计算分析
姜寿红
(1.交通部广州打捞局,广州 510290;2.广东省海洋工程施工与水上应急救援工程技术研究中心,广州 510290)
广东省在虎门大桥和港珠澳大桥之间的深中通道与港珠澳大桥类似之处是途径伶仃洋要采用沉管技术。沉管管节在隧址附近的预制场预制,管节在浮运过程中,采用多艘旁拖顶推保证管节航线稳定。途径的航道是浅水航道,并且遭受受潮汐流动影响,航道潮汐横流水流对管节的作用一个的横流,将导致管节偏航。管节和旁拖船体会使旁拖顶推时螺旋桨实际发出的推力会发生折损。依据经验,会预留20%~30%的推力折损补偿。
影响螺旋桨推力的因素是多方面的。有学者基于求解RANS方程的CFD软件平台,采用滑移网格技术模拟螺旋桨的旋转,选择标准-湍流模式数值模拟螺旋桨的推力等水动力。推力系数的预报误差最大可控制在4.3%以内。有学者采用多重滑移网格技术和计算流体力学方法,研究螺旋桨在水下潜器各子系统流场影响下作非定常转艏摆动时的推进特性。计算结果表明:水下潜器组合体流场对导管螺旋桨的推进特性有不可忽略的影响。有学者采用非定常RANS方程和RNG-湍流模型,使用滑移网格模拟螺旋桨旋转,对桨-舵系统的水动力进行数值模拟,结果表明,设计工况扭曲舵能提高敞水效率的效果。有学者采用数值模拟方法,基于RANS方程和RNG-湍流模型求解流场,利用滑移网格技术处理螺旋桨的旋转,研究偏转角对船后不同位置吊舱导管推进器的系柱推力和转矩影响,将数值模拟结果与模型试验结果比较,推力计算的最大误差为11.6%,绝大多数在5%以内。
本文问题主要涉及螺旋桨水动力性能和浅水航道大型钝体附体的绕流流动。螺旋桨水动力性能研究除了采用试验研究方法之外,还有大量的无空泡下的黏性数值模拟研究。文献[6-7]讨论了不同湍流模式对螺旋桨敞水性能计算结果的影响,发现不同湍流模式的计算结果比较接近;由于SST-湍流模式与标准-类似,加以改进,目前比其他湍流模型适用范围更广泛,在螺旋桨水动力性能计算中也被众多文献采用。并且数值模拟螺旋桨推力的结果与实验结果的误差在5%~10%,满足工程精度要求。
对于大型钝体浮体绕流问题的数值模拟,随着计算机性能的提升,可以实现原型计算,从而避免缩小模型计算中边界层流动和流动分离与原型的差别,使计算精度得到保证。本文采用基于RANS方程和SST-湍流模型,以及应用滑移网格技术实现螺旋桨的旋转运动,展开管节顶推时螺旋桨推力折损情况分析。计算模型采用实际尺度,包括管节、旁拖船、导管桨和浅水航道。管节在具有潮汐横流速度的浅水航道中浮运。考虑不同管节前进速度、不同航道横流速度和不同螺旋桨转速的影响,分别计算了旁拖位于管节一侧的前、后位置的流场流动,从计算结果中提取螺旋桨发出的推力,分析螺旋桨推力的折损情况。
1 数值模拟的理论基础
管节浮运可近似看做是管节的匀速直线前进,通过惯性坐标系转换,管节不动,而水流流向管节。同时,航道存在横流,旁拖的螺旋桨旋转。
流体不可压缩,考虑流体黏性,忽略重力的作用。流动由于螺旋桨的转动,非定常,并视为无空泡现象。忽略自由面波动的影响。
采用有限体积方法求解RANS控制方程,采用SIMPLEC算法进行压强与速度的耦合迭代求解,时间步进采用一阶隐式格式,其他均采用二阶迎风格式。
将以上方程结合流动的初始条件和边界条件,即可获得流场的流动和导管桨推力,进而分析螺旋桨的推力折损情况。
数值模拟方法首先建立模型,确定计算域,并将计算域划分网格完成流场空间的离散。然后将网格模型导入求解器,设置相关参数,最后运行求解。收敛标准取10,时间步长0.001 s。
2 建立数值模拟模型
计算模型包括管节、旁拖船、导管桨以及浅水航道。由于旁拖船和导管桨没有图纸,采用主要参数接近的拖船和导管桨代替,见图1。
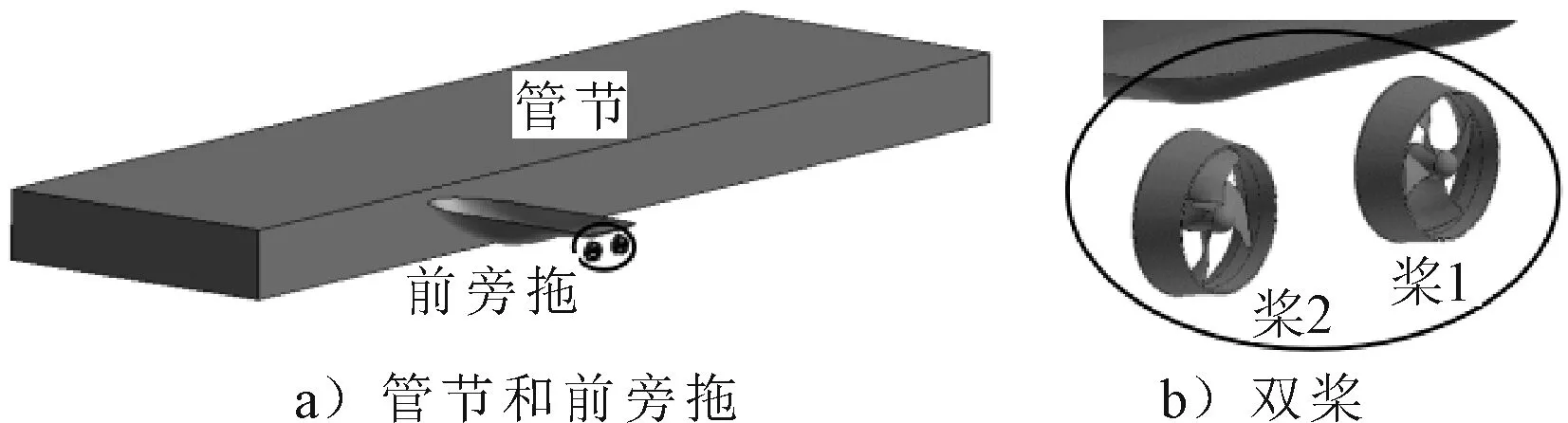
图1 管节、前旁拖和双桨模型(不含桨支撑结构)
管节为长方体,主尺度为:××=165 m×46 m×10.6 m,干舷取0.2 m。
旁拖船主尺度为:总长37.6 m、型宽10.5 m、型深4.5 m、吃水4.1 m、排水量784.78 t,双全回转导管桨,为外旋桨。
导管桨直径=2.5 m,平均螺距比()为1.145,盘面比为0.75,毂径比为0.167,右旋4叶桨。
实际上,旁拖顶推纠偏时,布置在管节侧面的前后位置,分别称为前旁拖和尾旁拖,两者相距99 m。可能前后分别布置一艘或者两艘船,并与管节有一定夹角。
为简化计算,考虑前旁拖与尾旁拖距离较远,忽略其相互影响,并仅计算单条前旁拖或尾旁拖。以及旁拖与管节的夹角也简化为只考虑拖轮与管节纵轴线垂直情况。
2.1 模型和计算域
在建模软件中,创建的管节、前旁拖或尾旁拖船、导管桨的模型,以前旁拖为例如图1所示。因为缺乏资料,模型中将固定螺旋桨的支撑结构部分省略了。尾旁拖相似。
计算域必须足够大才能保证计算精度,计算域和边界条件见图2。
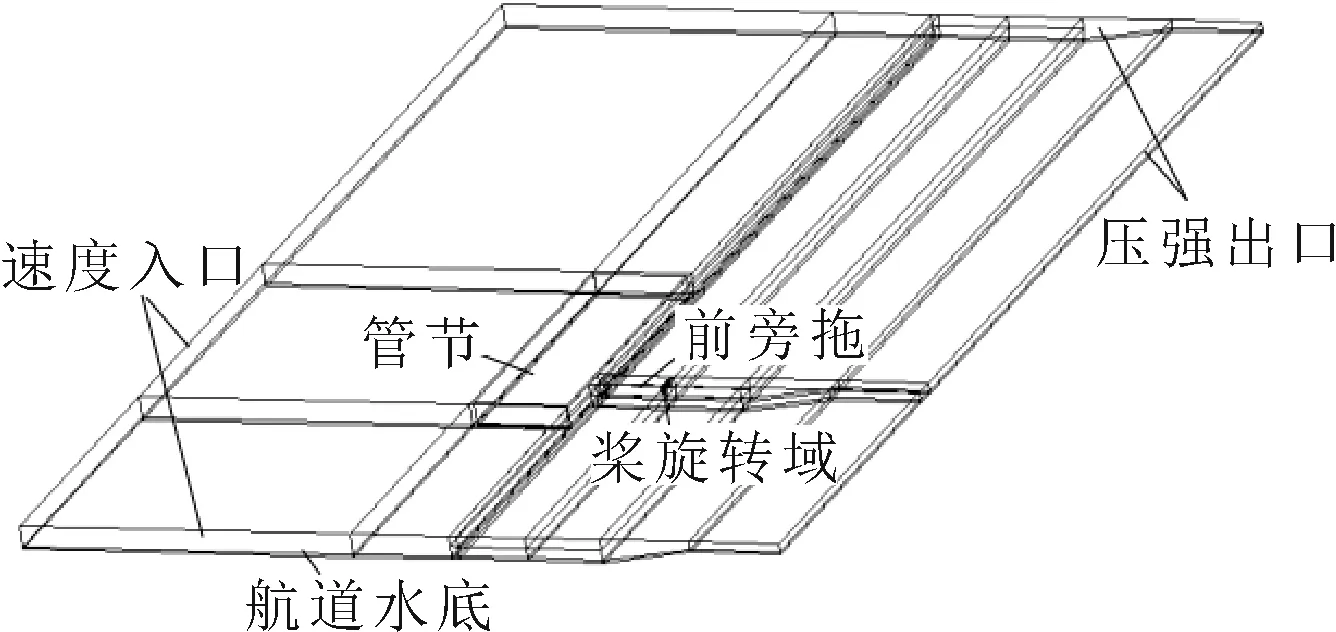
图2 前旁拖计算域和边界条件
为了保证横流到达管节的流速,将航道在横流流向管节一侧的形状做变化处理,另一侧保留实际航道水底的形状。
管节在有横流的浅水航道中浮运,计算域的边界包括水流流入的速度入口、水流流出的压强出口、航道水底,以及管节、船体、双桨的固壁面。
由于螺旋桨做旋转运动,在双桨附近各设置一个包含螺旋桨的旋转域。计算域中有动域,有静域。通过圆柱形交界面的相对滑移,实现螺旋桨的转动。为了划分不同类型网格,包括结构网格与非结构网格,加密网格与稀疏网格。
2.2 网格划分
数值模拟方法中,网格划分是关键。在流动变化快的地方,网格需要加密;离开管节远的地方,流动变化变缓,网格可以稀疏一些,以减小计算量。在固体壁面处,通过创建边界层网格以便更加准确模拟边界层的流动,见图3。
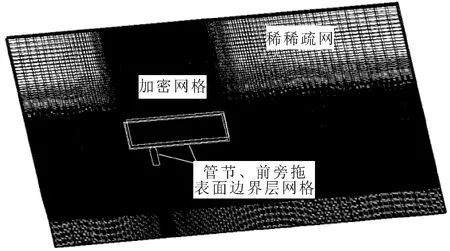
图3 前旁拖网格划分
管节尺度大且是钝体,计算域范围也大。而导管螺旋桨附近网格尺度与之相比小了4个量级。这不仅增加了网格划分的难度,网格数量也较多。前旁拖模型达网格数1 063万,尾旁拖为1 069万。
3 计算结果分析
3.1 敞水导管桨计算
首先计算直径为2.2 m的导管桨的敞水性能,计算结果与桨设计提供的数据比较见图4。
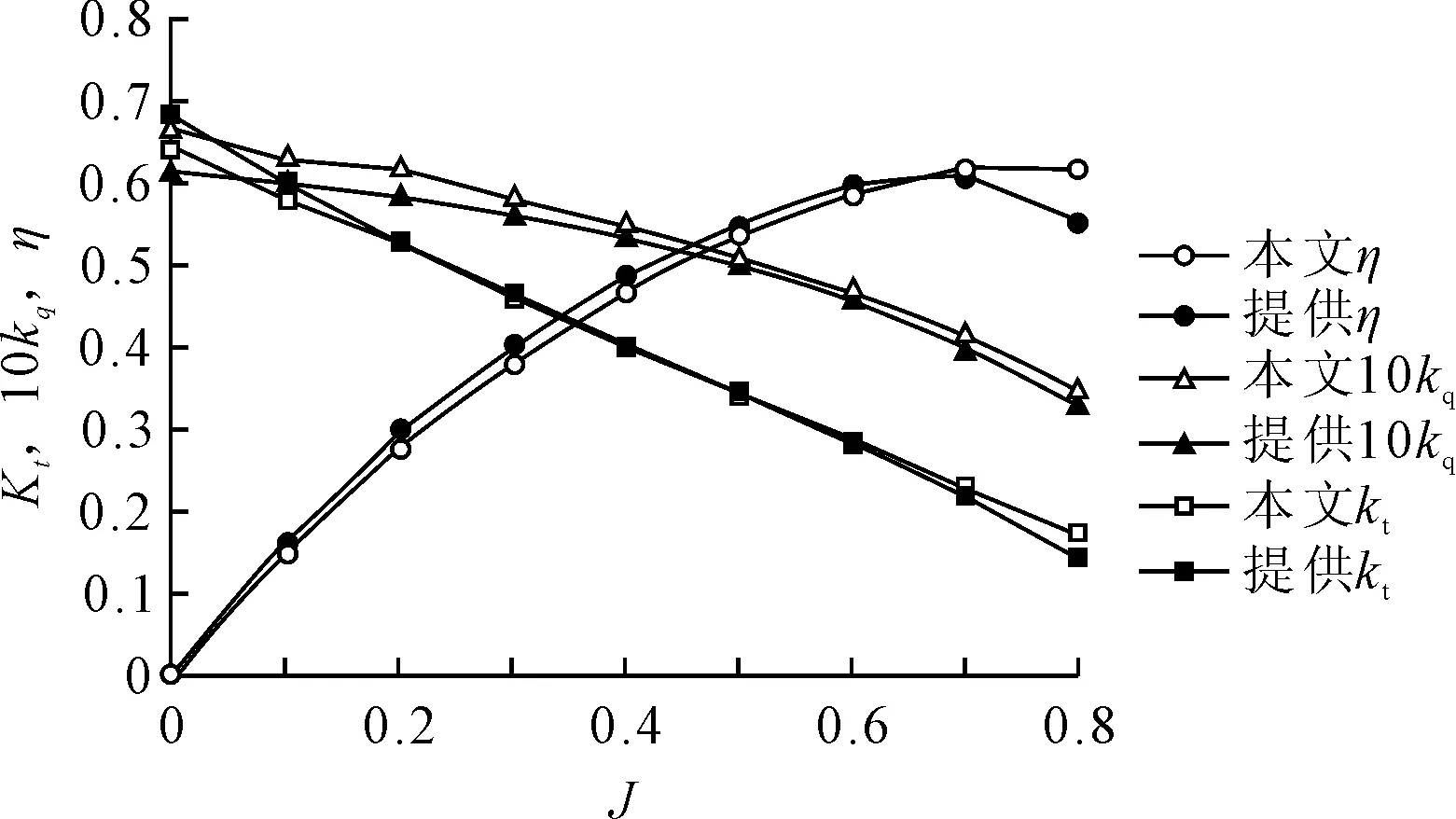
图4 直径2.2 m导管桨的敞水性能曲线
分析表明,进速系数在=0~07之间时,数值模拟的推力系数平均误差为2.7%,最大误差为4.75%;转矩系数平均误差为4.21%,最大误差为8.28%;敞水效率平均误差为4.21%,最大误差为8%。当进速系数>0.7时,误差增大。计算结果精度较好,满足工程要求,也表明采用的数值模拟方法和参数设置是可靠的。
对于项目需求直径为2.5 m导管桨建模,计算其敞水推力。
考虑最大横流速度为0.6 m/s,桨转速=215 r/min,进速系数=0.067,转速=247 r/min,进速系数=0.058,分别计算=2.5 m,=0,0.1时的推力,见表1。

表1 D=2.5 m导管桨敞水推力T0
3.2 导管螺旋桨推力折损分析
3.2.1 计算工况和推力折损计算方法
考虑旁拖位于管节前后位置和2个转速下,管节浮运速度和横流速度对旁拖推力的影响。2个转速:=215、247 r/min。
管节在浅水航道浮运时,管节前进速度不大于1.0 m/s,航道横流速度不大于0.6 m/s。计算工况取3个管节浮运速度:=0、0.5、1.0 m/s,和2种横流情况:=0、0.6 m/s。
每种工况下,桨或旁拖的推力用表示,推力折损率为
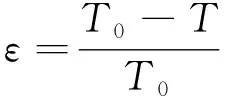
(1)
流场速度云图见图5。导管桨位于管节和旁拖的尾流区,流场是非均匀的。如果尾流流动定常的话,那么桨旋转1圈的过程中发出的推力应呈周期性变化。
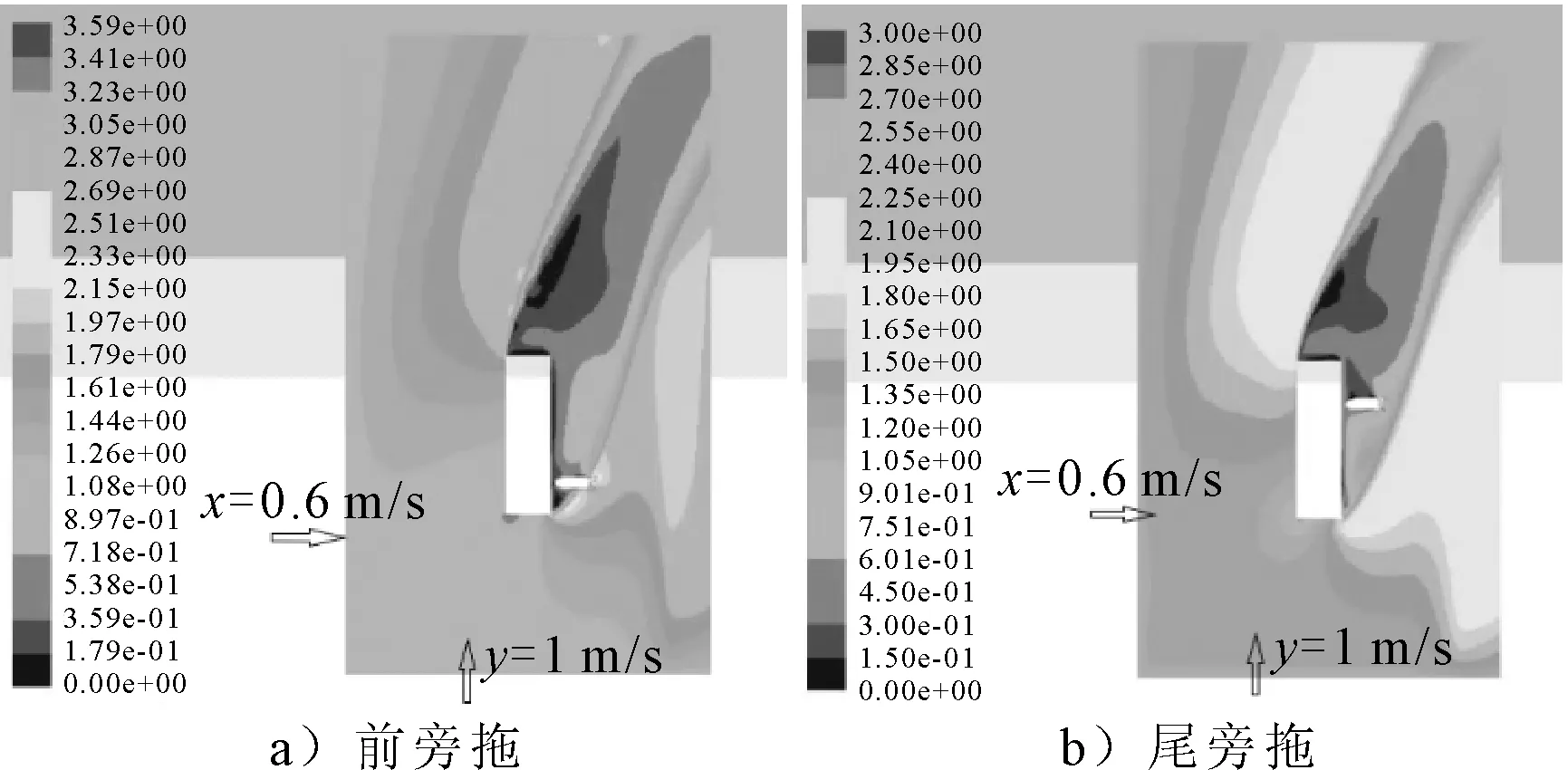
图5 n=215 r/min,V管节=1.0 m/s,V横流=0.6 m/s时流场的速度云图
转速=247 r/min、=1.0 m/s、=0.6 m/s时流场的速度云图与图5极其相似。
本文是4叶导管桨,转90°之后桨叶位置就重复了,桨或旁拖在定常非均匀的流场中发出的推力也循环重复了。
导管桨处的流场是非均匀的,所以以前旁拖导管桨为例,=1.0 m/s、=0.6 m/s,=247 r/min下,桨在90°以内每隔30°时的推力折损率,见表2。
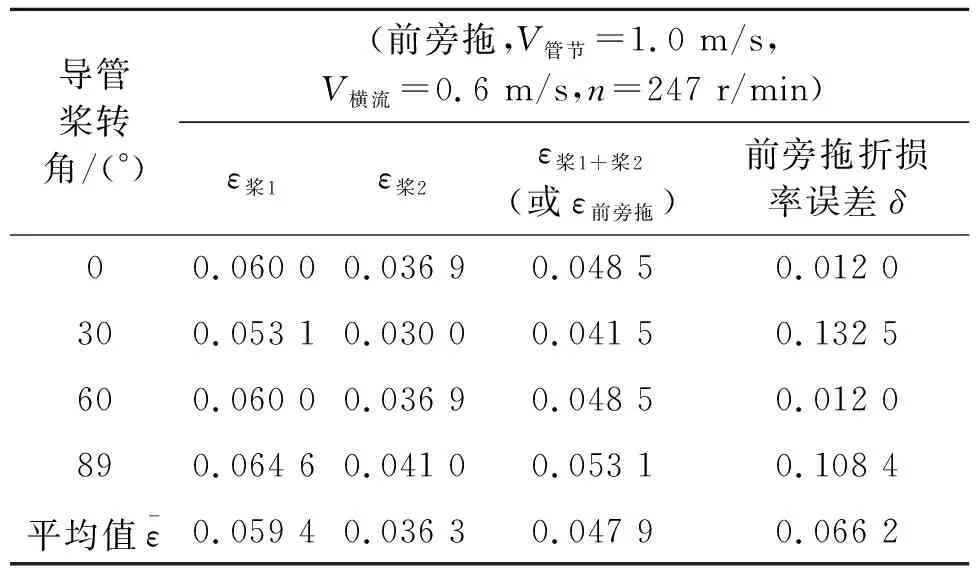
表2 导管桨不同转角下的推力折损率及偏差δ

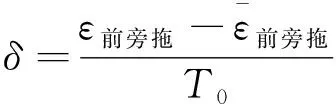
(2)
由于桨旋转1圈时推力折损率的波动不大,在满足工程精度下,保持相同转速下取相同的螺旋桨转角下的瞬时推力作为式(1)中的推力,进行折损率计算。
3.2.2 前旁拖折损率计算结果
横流速度为0、0.6 m/s时,管节速度变化时推力折损率见图6、7。桨1+桨2代表2桨发出的推力合力的折损率,代表1条前旁拖船推力的折损率。
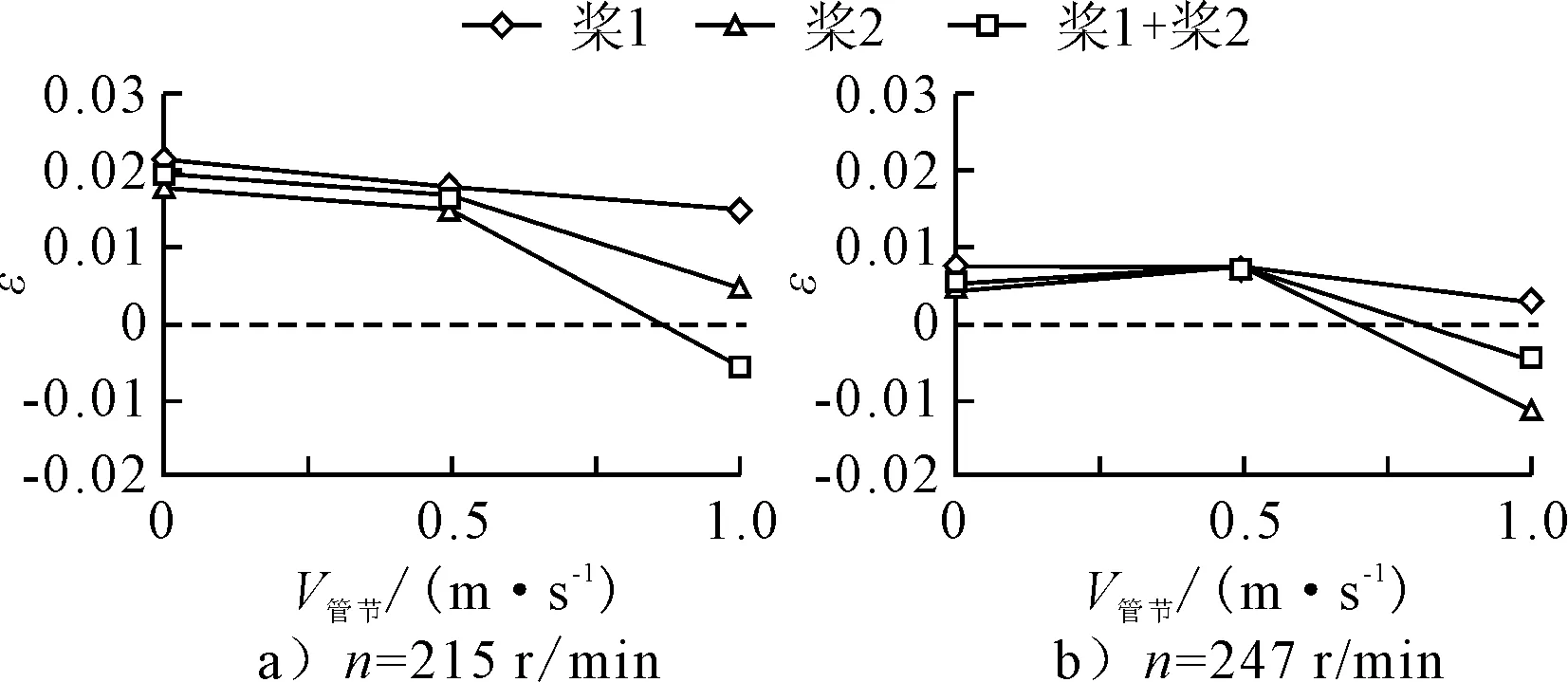
图6 V横流=0时前旁拖的推力折损率
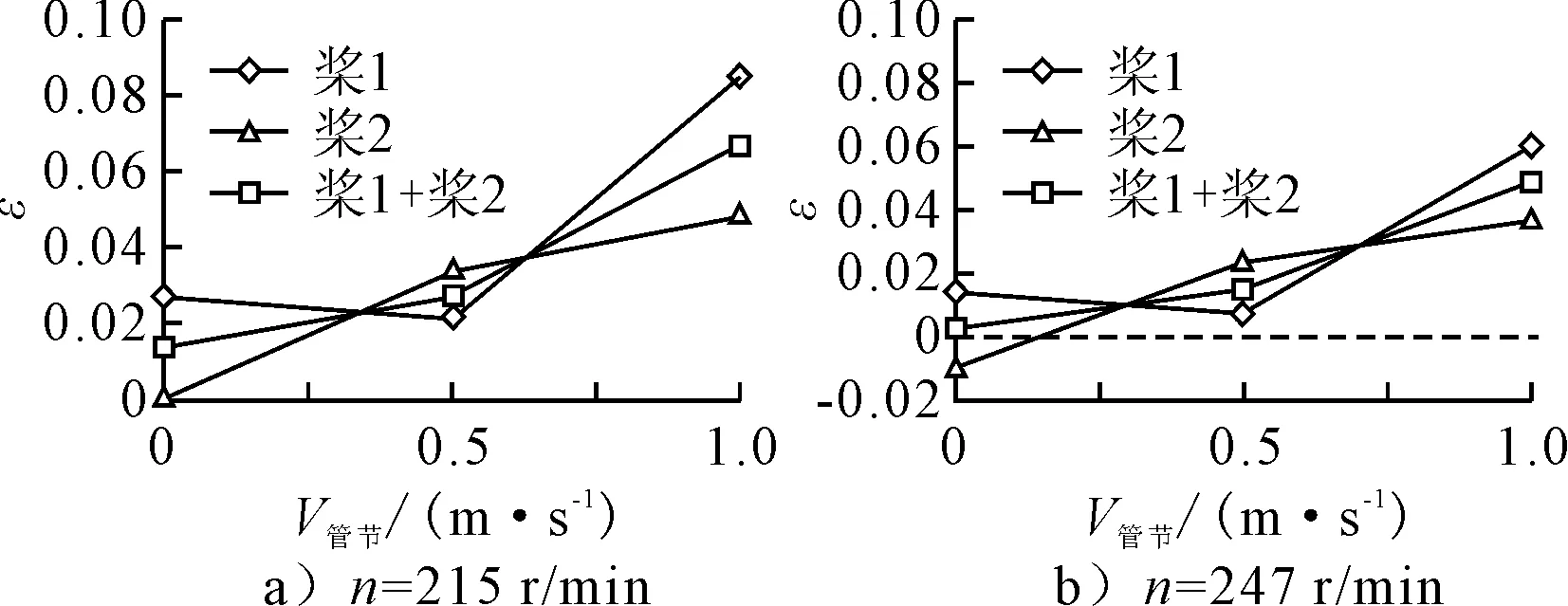
图7 V横流=0.6 m/s时前旁拖的推力折损率
从图6、7可见,相同横流速度,不同转速的推力折损率随管节速度的变化趋势一致,并且转速=215 r/min的折损率大于转速=247 r/min。
图6显示,无横流时,管节速度增加,导管桨1的推力折损率可能变为负值,这说明桨的来流速度方向的变化,使实际发出的推力可稍高于敞水推力。桨1和桨2的平均推力折损率,即前旁拖的折损率,总来讲很小。
图7显示,=0.6 m/s时,管节速度增加,桨1、桨2和前旁拖的推力折损率总的来说是增加的。最大推力折损率发生在=1.0 m/s和转速=215 r/min时,此时前旁拖船的推力折损率为6.6%。
3.2.3 尾旁拖折损率计算结果
横流速度为0和0.6 m/s时,管节速度变化时推力折损率的变化见图8、9。桨1+桨2同样为2桨发出的推力合力的折损率,代表1条尾旁拖的推力折损率。
图8 V横流=0时尾旁拖的推力折损率
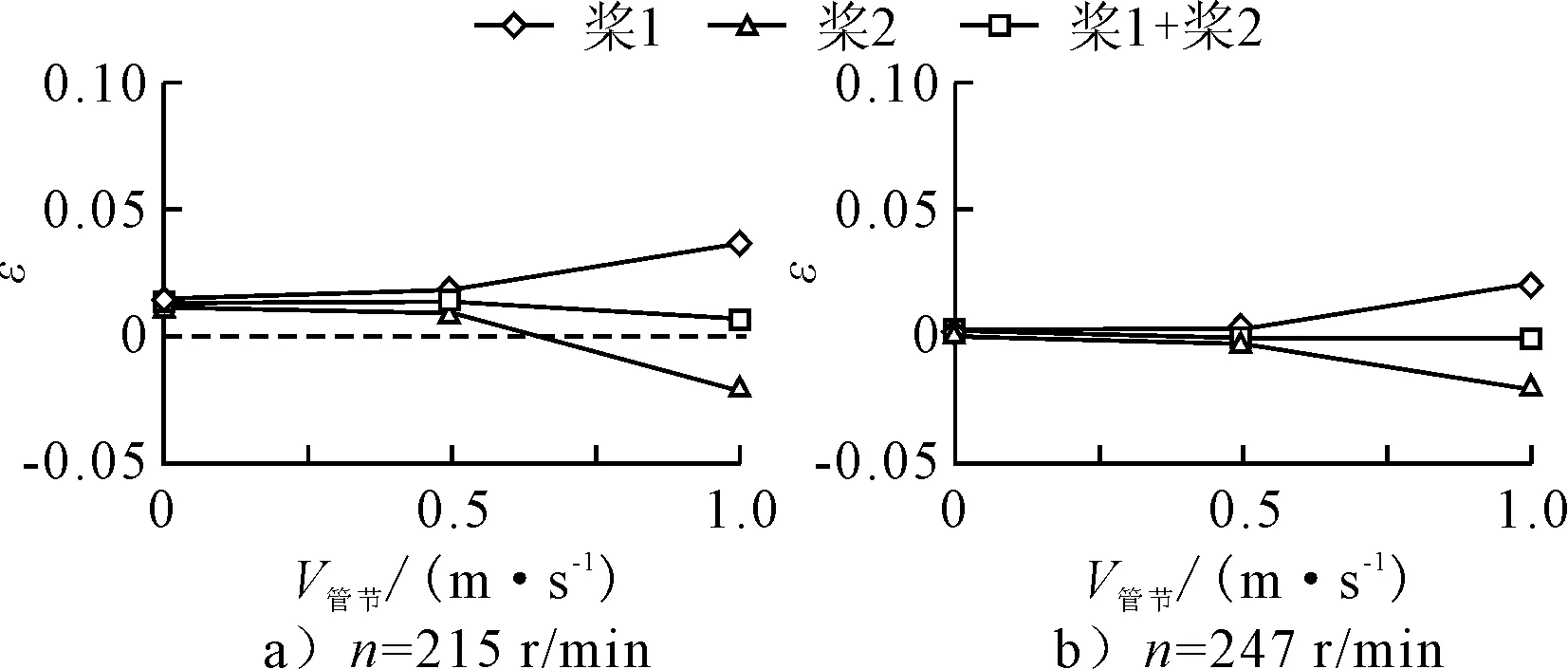
图9 V横流=0.6 m/s时尾旁拖的推力折损率
从图8、9可见:相同横流速度,不同转速的推力折损率随管节速度的变化趋势是一致的,并且转速=215 r/min的折损率大于转速=247 r/min。
图8显示,无横流时,管节速度增加,桨1、桨2和前旁拖的的推力折损率是增加的,并且管节速度=0.5 m/s的折损率与1.0 m/s的接近程度比与0的更加接近。最大推力折损率发生在=1.0 m/s和转速=215 r/min时,为9.4%。
图9显示,=0.6 m/s时,管节速度增加,桨2的推力折损率可能变为负值,这说明桨的来流速度方向的变化,使实际发出的推力可稍高于敞水推力。
4 结论
1)通过导管桨敞水性能计算,在进速系数小于0.7时,推力系数的计算误差小于5%,验证本文数值模拟的方法可行。
2)在其他因素相同的情况下,不同转速的推力折损率随管节速度的变化趋势是一致的,且较低转速=215 r/min的折损率大于较高转速=247 r/min。
3)尾旁拖所处的流场均匀度高于前旁拖,前旁拖的推力折损率高于尾旁拖。
4)计算单条旁拖最大推力折损率为9.4%,实际预留20%~30%足够补偿螺旋桨推力折损。

