基于广义稀疏逻辑回归的全脑分类

王 敬,张 宝,谢 晓,b,李 健,b,张 莉,b,郭华平,b

(信阳师范学院 a. 计算机与信息技术学院; b. 河南省教育大数据分析与应用重点实验室, 河南 信阳 464000)

0 引言

大脑解码,即从测量得到的生理数据推断大脑的认知状态,是揭示人脑奥秘的一个重要途径[1-2]。大量神经影像学研究已经证实了基于功能磁共振成像(functional magnetic resonance imaging, fMRI)数据预测被试大脑认知状态的可行性[3]。在相关研究中,传统的机器学习算法如支持向量机、线性判别分析、逻辑回归等得到了广泛应用[4-5]。然而这些算法不能充分利用fMRI数据的特点,因此将它们直接应用于大脑解码时存在局限性。

fMRI数据的主要特点包括维度高、样本数目少、蕴含空间结构等。传统机器学习算法应用到高维数据上时容易碰到维数灾难的问题[6]，通常解决这个问题的方法是通过主成分分析来降维,或者通过特征选择方法来提取与类别相关的特征。当数据维度高并且样本数目少时,传统的机器学习算法又容易产生过拟合的问题[6]。解决这个问题的常用方法是在分类模型中加入惩罚项。fMRI数据的前两个特点,即维度高和样本数目少,并非fMRI数据独有。比如在人脸识别中,人脸数据也常具备这两种特点。因此,维数灾难和过拟合的问题在机器学习和模式识别领域已经有了广泛和成熟的研究[6]。针对这两个问题,一种行之有效的解决方法是引入稀疏惩罚项[7]，稀疏惩罚项能够使得与分类无关的特征得到抑制,并且能够有效地避免算法的过拟合。已经有大量的稀疏算法[8-10]被应用到fMRI数据分析上。

对传统机器学习算法进行稀疏化改造，虽然可以避免维数灾难和过拟合问题,但仍无法利用到大脑的空间结构信息,因此在应用于全脑fMRI数据分类时存在不足。传统的机器学习算法通常要求将每个样本,比如二维人脸图像、三维全脑fMRI数据等,排列成一个一维向量,然后才能进行分析。将多维样本排列成一维向量会使得样本的维度信息丢失。人脸识别中的这个问题可以通过构造二维算法得到有效解决[11]。通过利用人脸图像的二维空间结构,该类算法能够在使用较少特征的前提下有效地提高分类准确率,然而这种思路无法直接推广到三维全脑fMRI数据上。要利用fMRI数据的空间结构,一种可行的方法是将表征空间结构的惩罚项引入到机器学习算法中[9,12-13]。

基于以上思路,本文在经典逻辑回归(Logistic Regression, LR)[8]算法的基础上，同时引入表征稀疏的惩罚项和表征空间结构的惩罚项,构建一种新的全脑fMRI数据分类算法,即广义稀疏逻辑回归(Generalized Sparse Logistic Regression, GSLR)算法,然后在优化最大化框架下，设计了一个迭代流程来求解该算法对应的优化问题,最后通过实验来证明该算法的有效性。

1 广义稀疏逻辑回归算法

1.1 稀疏逻辑回归算法

逻辑回归算法[8]常用于二分类。假设有n个样本类别对(xi,yi)(i=1,2,…,n),其中xi∈d为样本,yi∈{-1,1}为类别,样本之间互相独立且满足同一分布。定义X=[x1,x2,…,xn]∈d×n,y=[y1,y2,…,yn]T∈n。定义Sigmoid函数

(1)

根据逻辑回归模型,在已知权重向量w∈d和截距w0∈时,样本xi属于类别yi的概率可以表示为

σ(yi(w0+wTxi))。

(2)

已知训练样本及其对应的类别,通过最大化后验概率计算出w,然后将测试样本代入式(2),计算出该样本属于某一类别的概率,即可达到对测试样本进行分类的目的。通常构造增广矩阵来避免考虑w0,即xi←[1;xi],w←[w0;w],从而得到联合概率密度分布函数:

(3)

根据贝叶斯理论,在已知X和y的前提下,w的似然函数可以表示为

P(w|y,X)∝P(y|w,X)P(w),

(4)

最大化该似然函数即可求出w。

最大化式(4)中的似然函数,首先需要确定先验因子P(w)。假设权重之间不相关时,由广义正态分布理论,权重wj(j=1,2,…,d)的概率密度函数为

(5)

其中α、β、μ为调节参数。取均值μ=0,调节β可以得到两种常见的先验因子。β=1对应拉普拉斯先验因子:

(6)

β=2对应高斯先验因子:

(7)

将两种先验因子同时应用于式(4)中,然后对似然函数取对数可得式(8)的优化问题

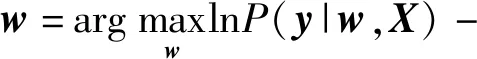
(8)

即同时带有l1范数和l2范数的稀疏逻辑回归算法,记作LR12。当λ1=0时,LR12退化为普通的逻辑回归算法,记作LR2。当λ2=0时,LR12退化为仅带l1范数惩罚项的逻辑回归算法,记作LR1。

拉普拉斯先验因子和高斯先验因子分别对应LR12中的l1范数和l2范数惩罚项。l2范数惩罚项也称岭(Ridge)惩罚项,能抑制无关特征对应的权重,避免过拟合。l1范数惩罚项也称拉索(LASSO)惩罚项,能使无关特征对应的权重缩减至零,从而得到稀疏的结果。岭惩罚项和拉索惩罚项结合在一起则构成弹性网(Elastic-net)惩罚项。该惩罚项同时具有岭惩罚项和拉索惩罚项的优点,因而得到了广泛应用。

1.2 空间结构惩罚项

为了利用大脑的空间结构信息,在高斯先验因子中对权重之间的相关性进行如下建模。假设两个特征wi和wj的坐标分别为(ai,bi,ci)和(aj,bj,cj),则wi和wj在三维空间中的距离为

(9)

定义邻接矩阵N=(Nij),

(10)

其中ε用来调节矩阵N的稀疏程度,ε越小,N越稀疏;δ用来调节矩阵N中非零元素的大小,δ越小,N中非零元素的值越小。在矩阵N的基础上定义精度矩阵Q-1如下:

Q-1=D-N,

(11)

(12)

以式(12)作为惩罚项代替式(8)中的l2范数惩罚项可得

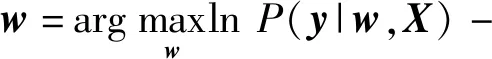
(13)

即广义稀疏逻辑回归(Generalized Sparse Logistic Regression, GSLR)算法。

GSLR算法基于两个特征的空间距离来调节两者权重的残差。直观地讲,两个特征wi和wj在空间上距离越近,由式(10)定义的邻接矩阵中对应的元素Nij越大,最大化式(13)时得到wi和wj的残差就越小。因此,GSLR可以保证特征w在空间上的连续性。

GSLR模型是已有的稀疏逻辑回归模型的泛化形式。当Q为单位阵时,GSLR退化为LR12。自然地,GSLR也是LR2和LR1的泛化形式。当

(14)

时GSLR算法退化为带GraphNet惩罚项的逻辑回归算法[12]。在不至于混淆的前提下,本文中将带GraphNet惩罚项的逻辑回归算法记作GraphNet。相对于其他几种稀疏逻辑回归算法,GSLR算法能更充分地利用特征的空间信息,预期可以在全脑分类上取得更好的效果。

GSLR与平滑稀疏逻辑回归(Smooth Sparse Logistic Regression, SSLR)[9]的主要区别在于构造了不同的空间结构惩罚项。GSLR中先用空间距离的高斯函数定义邻接矩阵N,然后通过式(11)计算出精度矩阵Q-1,而SSLR中直接使用空间距离的高斯函数来计算协方差矩阵Q。因此,GSLR可以退化为GraphNet,而SSLR则不行。另外,GSLR中可以通过调节参数ε改变邻接矩阵N的稀疏度,从而得到稀疏的精度矩阵Q-1,而SSLR中没有设置对应参数,计算得到的协方差矩阵Q是稠密的。考虑到全脑fMRI数据维度很高,稠密的协方差矩阵在存储和运算时都需要消耗更多的硬件资源。基于以上原因,GSLR选择与SSLR不同的方式来构造空间结构惩罚项。

1.3 迭代求解方法

在优化最大化(minorization-maximization, MM)[14]框架下构造 GLSR算法对应优化问题的迭代求解方法.令

l(w)=lnP(y|w,X),

(15)

则GSLR的目标函数可以写为

(16)

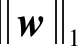
(17)

对l(w)在w(k)处进行二阶泰勒展开, 其中w(k)是w在第k次迭代后得到的结果,由中值定理可知,存在θ∈[0,1],使得

(w-w(k))。

(18)

定义

s=[σ(y1wTx1),…,σ(ynwTxn)]T=

σ(y°(XTw(k))),

(19)

其中：a°b表示Hadamard积,即向量a和向量b对应元素相乘得到的向量;Sigmoid函数σ(·)作用在向量上,表示对向量中的每个元素分别求Sigmoid函数,则l(w)的梯度和Hessian矩阵分别为

(20)

Xdiag[-(1n-s)°s]XT,

(21)

其中1n表示一个n行的全1向量。由式(21)可得

(22)

对于两个同样规模的矩阵A和B,A≥B表示A-B为半正定矩阵。 将式(20)和式(21)代入式(18),再结合式(22)可得

l(w)≥l(w(k))+(w-w(k))Tg(w(k))+

(23)

另外,由文献[11]知,

(24)

其中U=diag(abs(w(k)))-1。将式(23)和式(24)应用到式(17)中等式的右侧构造如下函数:

g(w|w(k))=l(w(k))+

(w-w(k))Tg(w(k))+

λρwTQ-1w。

(25)

该函数满足MM框架的两个条件,因此是一个合理的中间函数。根据MM框架,可以通过式(26)迭代地最大化g(w|w(k))来达到最大化f(w)的目的,

(26)

去掉g(w|w(k))中与w的无关项得

wT(g(w(k))-Bw(k))。

(27)

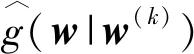
w(k+1)=(B-λ(1-ρ)U-2λρQ-1)-1·

(Bw(k)-g(w(k)))。

(28)

GSLR的优化过程如算法1所示。

------------------------------------

算法1 GSLR 算法

------------------------------------

输入:训练样本X,类别y

初始化:w(0)=1,k=0;λ、ρ、ε、δ、η=1,

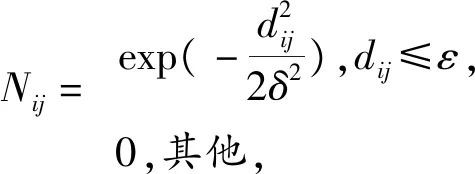
Q-1=D-N

whileη>10-4

s=σ(y°(XTw(k)))

g(w(k))=X[(1n-s)°y]

w(k+1)=(B-λ(1-ρ)U-2λρQ-1)-1·

(Bw(k)-g(w(k)))

k←k+1

end while

输出:w

------------------------------------

使用训练样本X及其类别y训练出w后,将测试样本代入式(2)中计算出该样本属于某一类别的概率,以此预测该样本所属类别。最后,结合预测类别和实际类别统计出分类准确率。

2 实验

2.1 fMRI数据集

实验中使用了两个公开数据集,即StarPlus数据集[15]和视觉物体识别(Visual Object Recognition, VOR)数据集[16]。关于两个数据集的详细描述如下。

StarPlus数据集采集的是被试观看图片和句子时的大脑fMRI数据。实验中选取了6个被试的数据,每个被试完成40个任务。每个任务要求被试首先看4 s句子/图片,接着看4 s空白屏幕,然后看4 s图片/句子,最后休息15 s。前20个任务先看句子后看图片,后20个任务先看图片后看句子。实验过程中,每秒采集两次大脑fMRI数据,仅扫描部分脑区,这些脑区对应20～30个解剖学上的区域。从StarPlus数据集中随机选取一个被试的某个时刻的大脑图像,是一个三维的灰度图像,其典型的切片图如图1所示。

图1 StarPlus数据示例图Fig. 1 An illustration of the StarPlus data

VOR数据集采集的是被试观看8种类别的图片时的全脑fMRI数据。8种类别的图片包括脸、房子、猫、瓶子、剪刀、鞋、椅子和混乱的图片。共6个被试参与实验,每个被试完成12个任务,每个任务选取8类图片各1张,随机打乱顺序,然后依次给被试观看。每张图片展示0.5 s,间隔1.5 s。从VOR数据集中随机选取一个被试,其典型的大脑图像如图2所示。

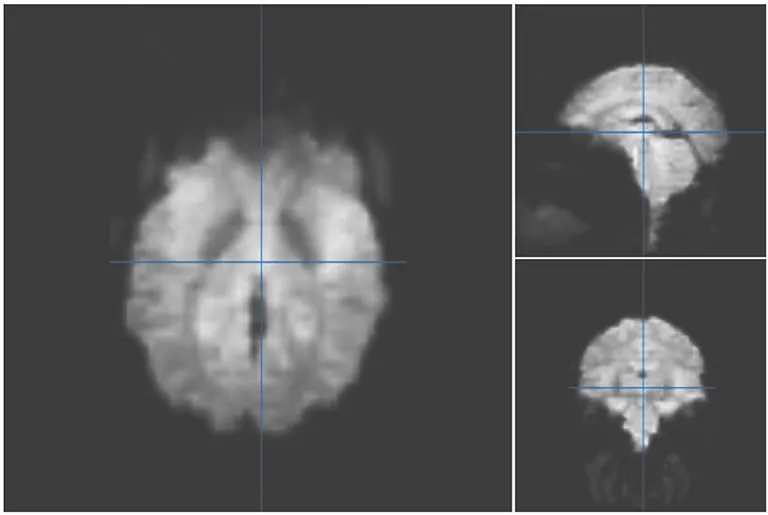
图2 VOR 数据示例图Fig. 2 An illustration of the VOR data

2.2 fMRI数据预处理

对于StarPlus数据集,网上公开的是已经预处理好的数据,无须额外的预处理步骤。对于VOR数据集,使用集成SPM12的静息态fMRI数据预处理工具DPABI[17],对原始数据进行预处理,包括以下步骤:首先校正不同切片的扫描时间差异,接着对齐图像以校正扫描过程中的头部运动,然后使用蒙特利尔神经学研究所模板大脑对图像进行标准化,使用三线性插值将图像重采样使得新图像分辨率为4 mm的立方,最后去除线性漂移。

2.3 实验设置

对StarPlus数据集和VOR数据集中每个被试的数据进行十重交叉验证,并计算平均分类准确率。具体地讲,将每个被试的所有样本随机等分为10份,每次取不同的1份用于测试,其他用于训练,计算分类准确率,然后将得到的10次分类准确率取平均,从而得到对于单个被试的分类准确率。将一个数据集中的所有被试对应的分类准确率取平均,得到对于该数据集的平均分类准确率,用来衡量算法的分类准确性。

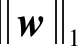
2.4 实验分析

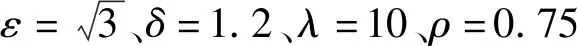
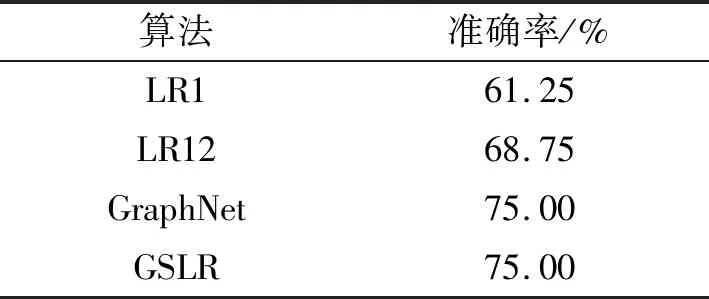
表1 4种算法在StarPlus数据集上的分类准确率Tab. 1 The classification accuracies of four algorithms on the StartPlus dataset

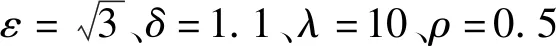
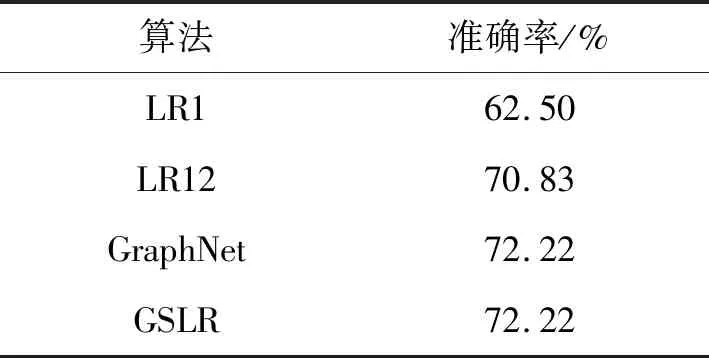
表2 4种算法在VOR数据集上的分类准确率Tab. 2 The classification accuracies of four algorithms on the VOR dataset

GSLR的最高分类准确率超过LR1和LR12的最高分类准确率,与GraphNet的最高分类准确率相等。与GraphNet相比,GSLR在构造邻接矩阵N时更加灵活:可以通过调节参数ε来调节改变邻接矩阵的稀疏度;可以通过调节参数δ可以调节邻接矩阵中非零元素的大小。因此,GSLR能够更加充分地利用到大脑的空间结构信息,在特征选择方面相对于GraphNet具有优势。

3 总结和展望

将表征稀疏的惩罚项和表征空间结构的惩罚项同时引入逻辑回归中,特别是设计了一种具有一般性的表征空间结构的惩罚项,从而提出了一种新的广义稀疏逻辑回归算法。该算法是多种已有的稀疏逻辑回归算法的泛化形式。实验结果表明,本文提出的算法相对于已有算法在全脑fMRI分类上具有明显优势。另外,由于本文提出的算法能够更加充分有效地利用大脑的空间结构信息,因此相对于其他方法更适合用于特征选择。

本文存在一些不足之处需要在今后的研究中加以改进。一是使用到的数据种类和数量都有限,没有充分体现不同算法之间的差距。二是有必要以更精细的粒度来调节邻接矩阵中的参数,从而找到最有利于分类和特征选择的参数组合。