P-集合的动态边界特征与信息动态融合生成
张秀全,张俊艺,史开泉
(1. 黄淮学院 数学与统计学院, 河南 驻马店 463000; 2.山东大学 数学学院, 山东 济南 250100)
0 引言
文献[1]在普通集合(经典cantor集)中补充了“动态特性”并提出P-集合概念,进而弥补了经典集合只具有“静态特征”的不足,使得P-集合在数据智能挖掘与获取、健康大数据等动态信息问题中得到广泛应用[2-3]。P-集合的对偶形式为逆P-集合[4],其在信息智能隐性传递、数据扰动挖掘等领域得到应用[5-6]。P-集合的函数形式为函数P-集合[7],它是动态信息规律模型,在信息伪装、风险识别中有广泛应用[8-9]。给定普通元素集合X,P-集合的边界特征为:
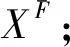
2.X的边界向外扩展,X生成外P-集合XF;
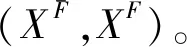
P-集合的边界变化来自有限普通元素集合X的属性集合的变化。这个事实在动态信息(数据)应用研究中被经常遇到,特别是在信息动态融合应用研究中。在某种意义下,P-集合表现了动态系统的实际面貌。在应用中,一个有限普通元素集合X与它的属性集合α相伴;或者,X与α同步出现。若定义有限普通元素集合X是有限信息(x),或者(x)=X,从P-集合的结构中得到:
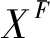
B.若X的属性集合α内删除属性,则X内被补充一些元素,外P-集合XF被生成;或者,当(x)内补充一些信息元,外P-信息融合(x)F被生成。
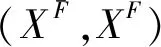
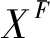
根据边界特征1—3与A—C的对应关系,启发我们提出以下3个问题:
1)P-集合是否可以用来研究P-信息动态融合;
2)P-集合研究信息融合能得到什么样的基础理论结果;
3)P-集合动态边界特征与信息融合存在怎样的关系。
本文利用P-集合与信息融合交叉,给出这些问题的基本理论研究。主要结果有:给出P-集合动态结构介绍,定义了信息融合的概念,证明了信息动态融合属性补充定理、属性删除定理、属性补-删定理;给出P-集合边界动态度、信息动态融合系数概念,证明了内P-边界动态度与内P-信息动态融合系数定理、外P-边界动态度与外P-边界动态融合系数定理、P-边界动态度与P-信息动态融合系数定理,给出属性合取扩展-收缩逻辑关系。
1 P-集合的结构与动态特征
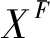
(1)
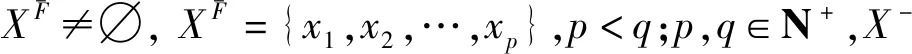
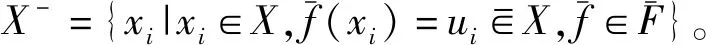
(2)
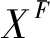
(3)
这里:βi∈V,βiα。
给定有限普通元素集合X={x1,x2,…,xq}⊂U,α={α1,α2,…,αk}⊂V是X的属性集合,称XF是被X生成的外P-集合,简称XF是外P-集合[1],
XF=X∪X+,
(4)
这里:XF={x1,x2,…,xr},q X+={ui|ui∈U,uiX, (5) (6) 有限普通元素集合X称为P-集合的基集合(基础集合)。 由式(3)可给出 (7) 进而满足式(7)的内P-集合为 (8) 由式(6)可给出 (9) 进而满足式(9)的外P-集合为 (10) 利用式(8)和式(10)得到 (11) 式(11)称为X生成的P-集合族,式(11)是P-集合的一般表达式,其中I,J为指标集合。 约定:下面的讨论中,X与(x)不加区分地混合使用,X是集合,(x)是信息;∀xi∈X是X内的元素,∀xi∈(x)是(x)内的信息元。 (12) 定义2 如果存在信息Δ(x)≠∅, Δ(x)∩(x)=∅;(x)F、(x)、Δ(x)满足 (x)F=(x)∪Δ(x), (13) 则称(x)F是被(x)生成的外P-信息融合。 定义4 称集合 (14) 是由(x)生成的P-信息动态融合族。 αF-(α∪Δα)=∅ 。 (15) (16) 推论2 若(x)的属性集合α被删除属性集合∇α,则具有属性集合(α-∇α)的(x)F是(x)生成的外P-信息动态融合。 由定理1、定理2及推论1、推论2直接得到定理3和推论3。 (17) 由以上定理和推论可以得到: 命题2 在属性集合α内删除属性集合∇α的条件下,(x)外的一些信息元xj补充到(x)内,(x)生成外P-信息动态融合(x)F。 (18) ρF=card(XF)/card(X), (19) 其中,card=cardinal number(基数)。 (20) μF=card((x)F)/card((x))。 (21) 由定义5—定义8得到: (22) 由定义7可得 进而有 定理5(外P-边界动态度与外P-信息动态融合系数定理) 若(x)F是XF生成的外P-信息动态融合,则XF的外P-边界动态度ρF与(x)F的外P-信息动态融合系数μF满足 ρF-μF=0 。 (23) (24) 命题5 (x)F是XF生成的外P-信息动态融合,则(x)与X内被补充相同的元素xj。 (25) 定理8 若(x)F是XF动态生成的外P-信息动态融合,则∀xj∈(x)F的属性αj,∀xj∈XF的属性αj具有相同的属性合取范式收缩,或者 (26) (27)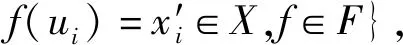

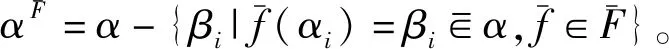
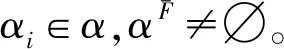
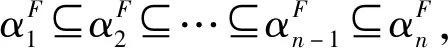

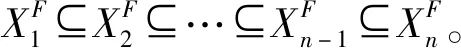
2 信息动态融合生成与属性补-删定理
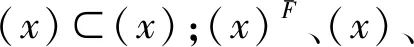

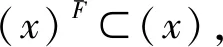
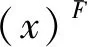
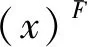
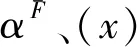
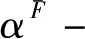

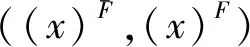
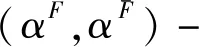
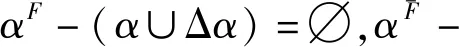

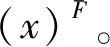
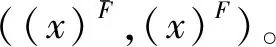
3 P-集合的动态边界与信息动态融合关系
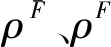
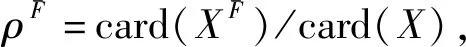
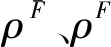

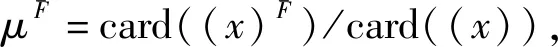

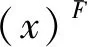
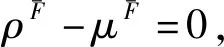
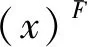

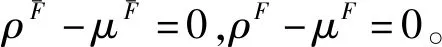



4 结语