一类具有阶段结构的蚜虫生物控制系统研究
黄明湛, 刘守宗, 张 莹
(信阳师范学院 数学与统计学院, 河南 信阳 464000)
0 引言
蚜虫是一类植食性昆虫,在世界范围内的分布十分广泛,但主要集中于温带地区,因此对中国的农业作物影响极大。小麦蚜虫是我国小麦的重要害虫之一,每年都不同程度地发生。蚜虫不仅吸取植株汁液,影响作物发育,还能传播多种病毒疾病,可造成粮食严重减产。以化学杀虫剂为主的传统防治技术具有环境污染等诸多问题,而且可持续农业的发展促使人们加快推进各类农作物病虫的全程绿色防控。因此,针对蚜虫的生物防治是推进绿色发展、改善环境和增强粮食安全及生态系统保护力的重要举措。
蚜虫的生物防治,就是利用蚜虫的天敌来控制或减轻蚜虫虫害。蚜虫在自然界的天敌很多,有昆虫、真菌、细菌、病毒和鸟类等[1-2]。目前已有的观察和研究表明,一些昆虫(如瓢虫)对田间蚜虫的数量变动有明显的影响[2]。针对蚜虫及其生物天敌相互作用的动力系统,已有大量学者进行了深入的研究[3-8]。例如文献[3]研究了利用七星瓢虫控制蚜虫,构建了具有阶段结构的捕食者-食饵模型,考虑了两种群所有阶段的相互作用关系,其数值分析的结果显示,初始状态下的天敌害虫比率是生物控制的关键因素。文献[4]利用时滞微分方程研究了具有七星瓢虫阶段结构的蚜虫-七星瓢虫系统模型。文献[5]建立了具有食蚜蝇阶段结构的蚜虫-食蚜蝇模型。
作为蚜虫的天敌,七星瓢虫在一生中要经过卵、幼虫、蛹和成虫四个不同发育阶段,其中幼虫和成虫均可捕食蚜虫,不同阶段对蚜虫的捕食能力不同,而蛹期则是保持不吃不喝。为了对蚜虫虫害进行有效生物防治,在合适时间向田间释放不同生长阶段的七星瓢虫成为一种重要手段。为了考查不同阶段蚜虫的捕食能力,研究者在实验室中会选择释放不同的虫态,观察其灭蚜效果。本文针对实验室中研究幼虫阶段的七星瓢虫治理蚜虫的效果构建数学模型,继而探讨蚜虫生物防治的策略。
1 建立模型
文献[6]在研究蚜虫种群的动态变化规律时,利用了广义的Logistic种群动态模型,并考虑了温度和相对湿度的影响。在此基础上,本文构建如下蚜虫种群动态模型:
bx(t)g(t,y(t)),
(1)

在实验室中研究七星瓢虫幼虫的捕食过程中,为了避免混淆,幼虫将会被定期释放,且幼虫到达蛹期即被取出。不同龄期的幼虫的捕食能力不同,一般来说3龄、4龄幼虫捕食能力高于1龄、2龄幼虫。为方便起见,本文将幼虫的捕食能力分为两个层次,在初期阶段捕食能力相对较低,一定时间之后,捕食能力达到较高水平。此外,蚜虫的生长也是分阶段的,不妨考虑卵和成虫两个阶段,并假设七星瓢虫仅捕食成年蚜虫。为此,在模型(1)的基础上,构建如下时滞微分系统:
hx(t)-bx(t)g(t,y(t)),
(2)
其中:x(t)=x0>0,t∈[-τ,0],τ表示蚜虫的生长时滞。

此外,假设每隔时间T,释放数量为c的七星瓢虫初期幼虫。由于蛹期的瓢虫不具有捕食能力,且在成虫之前被取走,所以当w=T(即瓢虫的释放周期恰好等于其幼虫期)时,有
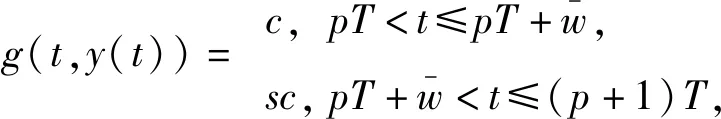
(3)
其中p=0,1,2,…。
当w g(t,y(t))= (4) 其中p=0,1,2,…。 g(t,y(t))= (5) 其中p=1,2,…。 g(t,y(t))= (6) 其中p=1,2,…。 下面将依据七星瓢虫的释放周期,分三种情况研究系统(2)中蚜虫的种群动态变化规律。 在系统(2)中,函数g(t,y(t))是具有脉冲属性的分段函数,这导致系统(2)为时滞脉冲动力系统。在对该系统的研究中,除了关注蚜虫灭绝平衡点,还将考虑在什么情形下蚜虫种群数量存在周期性变化,也即系统(2)的正周期解的存在性。 f(u1,v1,t)-f(u2,v2,t)≤ k(|u1-u2|+|v1-v2|); (7) 那么,方程 x′(t)=f(x(t),x(t-τ),t),t∈R, (8) 引理2 考虑函数 其导函数 当v≠0时,G′(x)的两个零点分别记为 有如下结论: 当T=w时,系统(2) 转化为如下形式: (9) 其中p=0,1,2,…。令 f1(x(t),x(t-τ))= q(x(t-τ))-(h+bc)x(t), f2(x(t),x(t-τ))= q(x(t-τ))-(h+bsc)x(t)。 假设r(e)>h+bsc,可以得到 其中 ξ1=r(e)+v(h+bc), ξ2=r(e)+v(h+bsc), 容易得到x1>x2。 定理1 假设r(e)>h+bsc且T=w,若下述三个条件之一成立: 则系统(2)存在一个连续、分段C1光滑、周期为T的周期解x(t),且满足x2≤x(t)≤x1,t∈R。 证明当T=w时,系统(2)等价于系统(9)。 令 f(u,v,t)= (10) 其中:p=0,1,2,…;(u,v,t)∈Ω=[0,+∞]×[0,+∞]×R。 根据引理1,将式(10)视为方程(8)对应的函数f(u,v,t),依据fi(i=1,2)的表达式以及xi(i=1,2)的定义,可得 f(x1,x1,t)≤0,f(x2,x2,t)≥0,t∈R。 当w (11) 其中p=0,1,2,…。 令 f3(x(t),x(t-τ))=q(x(t-τ))-hx(t), 假设r(e)>h+bsc,可以得到 其中 容易得到x3>x1>x2。基于上述讨论,可以得到下述结论: 定理2 假设r(e)>h+bsc且w 则系统(2)存在一个连续、分段C1光滑、周期为T的周期解x(t),且满足x2≤x(t)≤x3,t∈R。 证明当w f(u,v,t)= (12) 其中:p=0,1,2,…;(u,v,t)∈Ω。 再根据引理1,将式(12)视为方程(8)对应的函数f(u,v,t),依据fi(i=1,2,3)的表达式以及xi(i=1,2,3)的定义,可得 f(x3,x3,t)≤0,f(x2,x2,t)≥0,t∈R。 (13) 其中p=1,2,…。 令 f4(x(t),x(t-τ))= q(x(t-τ))-(h+b(s+1)c)x(t)。 假设r(e)>h+b(s+1)c,则可以得到 f4(x,x)=q(x)-(h+b(s+1)c)x= 其中 ξ4=r(e)+v(h+b(s+1)c), 容易得到x1>x2>x4。基于上述讨论,可以得出下述结论: 则系统(2)存在一个连续、分段C1光滑、周期为T的周期解x(t),且满足x4≤x(t)≤x1,t∈R。 (14) 其中:p=1,2,…;(u,v,t)∈Ω。 再根据引理1,将式(14)视为方程(8)对应的函数f(u,v,t),依据fi(i=1,2,4)的表达式以及xi(i=1,2,4)的定义,可得 f(x1,x1,t)≤0,f(x4,x4,t)≥0,t∈R。 (15) 其中p=1,2,…。 令 f5(x(t),x(t-τ))= q(x(t-τ))-(h+2bsc)x(t)。 假设r(e)>h+2bsc,可以得到 f5(x,x)=q(x)-(h+2bsc)x= 其中: ξ5=r(e)+v(h+2bsc), 容易得到x1>x2>x4>x5。基于上述讨论,可以得出下述结论: 则系统(2)存在一个连续、分段C1光滑、周期为T的周期解x(t),且满足x5≤x(t)≤x1,t∈R。 f(u,v,t)= (16) 其中:p=1,2,…;(u,v,t)∈Ω。 再根据引理1,将式(16)视为方程(8)对应的函数f(u,v,t),依据fi(i=1,2,4,5)的表达式以及xi(i=1,2,4,5)的定义,可得 f(x1,x1,t)≤0,f(x5,x5,t)≥0,t∈R。 本节通过数值模拟来验证前面的理论结果。由于蚜虫的内禀增长率r(e)是一个跟温度相关的函数,这里为了方便起见,不再引入该函数变化形式,直接对r(e)≜r进行赋值。 图1 当T=w=5时,系统(2)的时间序列图Fig. 1 Time series of system (2) for T=w=5 图2 当w 图3 当时,系统(2)的时间序列图Fig. 3 Time series of system (2) for T 图4 当时,系统(2)的时间序列图Fig. 4 Time series of system (2) for T 建立了一种带有生长阶段和脉冲释放的蚜虫种群动力学模型。基于实验室中特定的实验目的,仅考虑幼龄阶段七星瓢虫的释放,同时根据不同幼龄期捕食能力的差别,将瓢虫按照捕食能力再进行区分。针对构建出的时滞脉冲微分方程系统,利用不动点理论,给出了多种情形下,蚜虫种群数量呈现周期性变化的条件。同时,利用数值模拟,证实在各种情形里,都可以通过调整瓢虫的释放策略,以达到使蚜虫灭绝的结果。

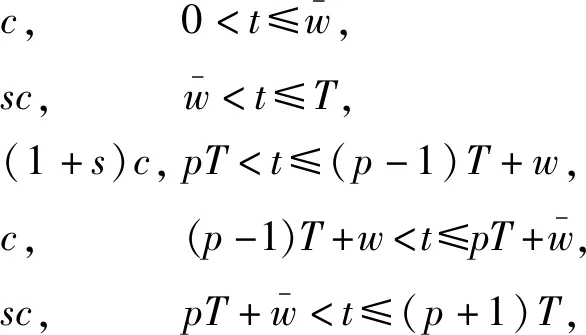
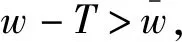

2 周期解的存在性
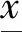





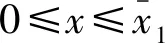
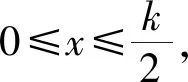

2.1 情形T=w


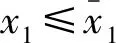


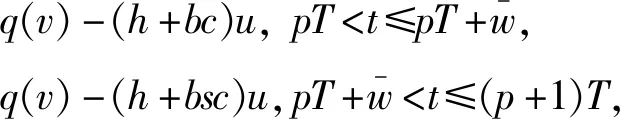
2.2 情形w


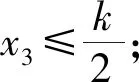

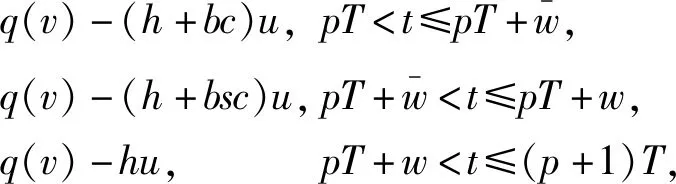
2.3 情形


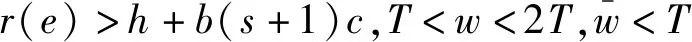
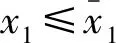



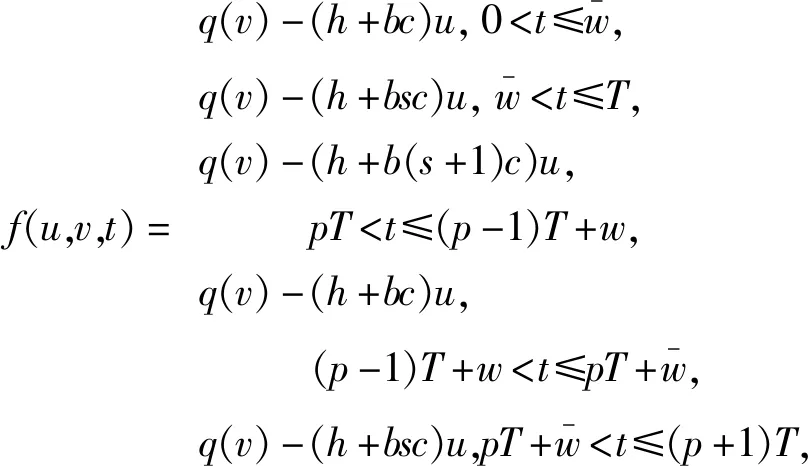

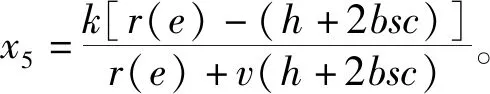

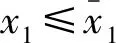




3 数值模拟





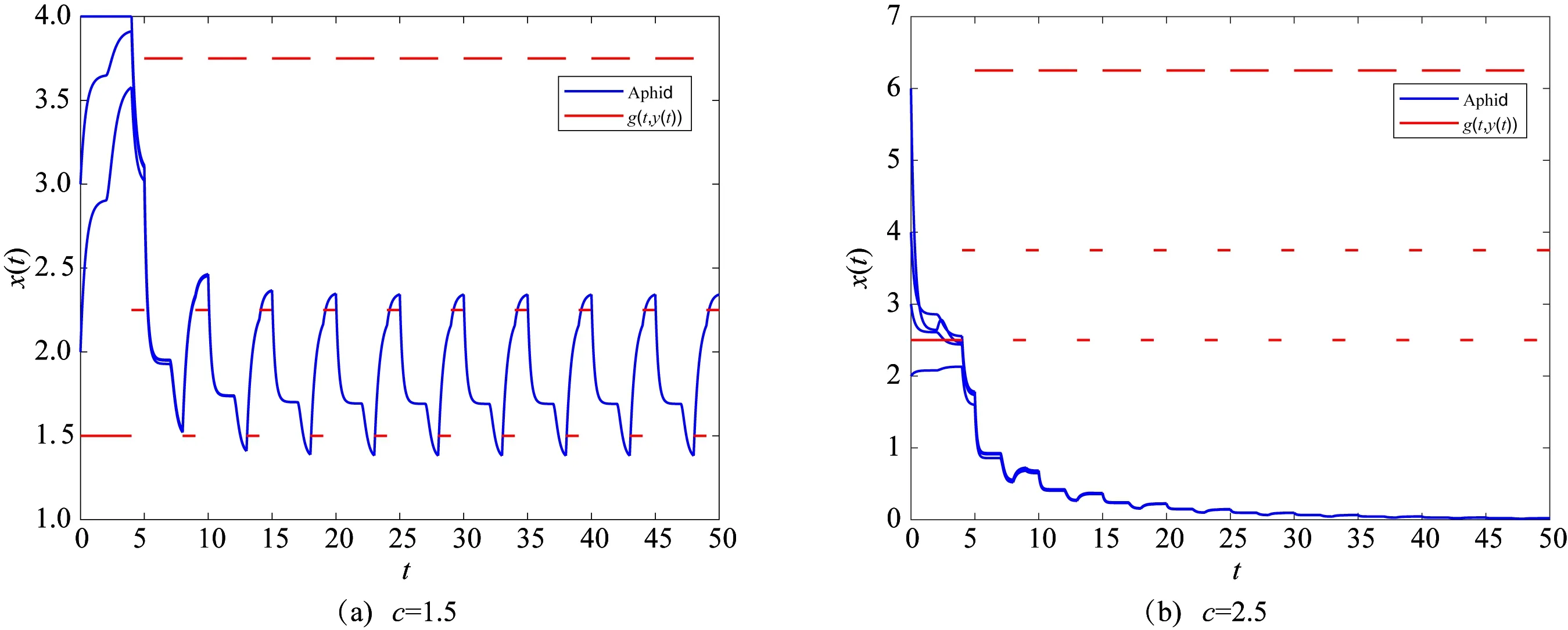


4 结语

