基于混沌映射和交换置换的自适应图像加密算法
叶瑞松,习玉婷,陈锦彬
(汕头大学 数学系,广东 汕头 515063)
随着智能手机和移动互联网的快速发展,图像信息的获取与共享交换日益方便快捷.网络上传输的图像信息会被非法截获、篡改,图像信息的安全问题也日益受到更多的关注.加密是一种有效的保护机密信息的技术,一些传统的数据加密算法,如RSA,IDEA、AES 等,对于具有高度相关度和冗余度等内在特征的数字图像来说并不适合[1].混沌系统具有对初值和系统参数的敏感依赖性,拓扑转迁性,伪随机性等特点,这些特点和密码系统混淆扩散的基本要求高度一致,使得基于混沌映射的图像加密算法具有很好的加密性能[2-3].
基于混沌的图像加密算法一般采用置换-扩散结构,这是由Fridrich于1998年首次提出的[2].这种加密由两个过程组成:置换和扩散.基于这种置换-扩散结构,许多学者提出了一系列基于混沌的加密方案[4-7].传统的具有固定密钥流的置换-扩散体系结构存在一个很大的缺陷.如果明文图像是一个所有像素的灰度值相同的均匀图像,则置换和扩散阶段将变成两个相互独立的过程.黑客可以容易通过已知明文或选择明文攻击进行密码分析,并成功破解[8-11].为了克服传统的混沌图像加密方案密钥空间小、置换-扩散结构安全性差等缺点,许多研究者转向寻找具有大密钥空间和有效置换-扩散机制的改进混沌图像加密系统.文献[3]提出了一种具有高效置换-扩散机制的图像加密方案,该方案具有巨大的密钥空间、有效抵抗统计攻击、差分攻击、已知明文以及选择明文攻击等优点.文献[12]利用Logistic映射和正弦映射的非线性组合构造了一个新的改进混沌系统,采用该混沌系统获得更好的安全性和加密性能.文献[13]使用Chen系统生成具有优良混沌性能的密钥流,并设计了一种基于动态状态变量选择机制的混沌图像加密方案(DSVSM)以提高图像加密的安全性和性能.文献[14]提出了两种图像加密算法.算法1在置换过程中使用Cat映射,扩散阶段使用Logistic映射,而在算法2中,置换阶段由反向Cat映射和普通Cat映射组合而成,在两个置换步骤之间进行像素值修改.文献[15]提出了一种新的基于格雷码置换的图像加密方案,其置换策略利用了(n,p,k)-格雷码的优点来获得优良的置换效率,其扩散过程具有明文相关的特性.文献[16]提出一个基于混沌和伽罗瓦域运算的新型彩色图像加密算法.该算法采用伽罗瓦域上扩散与置换相嵌-颜色通道间置换-双向扩散的加密结构.该算法具有极大的密钥空间、良好的统计特性、极强的密钥敏感性、明文敏感性,可有效抵抗多种攻击.文献[17]提出了一种以混沌系统的初始值和参数作为密钥,主要采用改进的Joseph 遍历法对图像进行加密.文献[18]提出了一种基于比特反转的增强型数字混沌映射,可以有效增强密钥流的混沌特性.
本文提出了一种基于混沌映射和像素交换的图像加密算法.该算法在以下几个方面进行了创新,较好地解决了经典置换-扩散结构的图像加密方案所存在的缺陷.1)通过斜帐篷映射生成与明文图像像素灰度值相关的随机位置分配.这意味着即使用相同的密钥加密不同的明文图像时,密钥流也会不同,攻击者无法通过已知/选择明文攻击获取任何有用的信息.因此,本文提出的图像加密算法具有自适应的特性,可以达到一次一密的加密效果.2)正如许多现有的工作所指出的,扩散过程是整个加密方案中代价最高的[19].本文提出的基于像素交换的置换方法可以同时产生混淆和扩散效应,从而加快加密速度,有效地解决了扩散过程耗时的问题.3)该加密算法中的扩散过程以S形模式扫描实现,在扩散阶段明文的微小差异将导致整幅密文图像的巨大差异,因此可以获得更有效的扩散效应.论文对加密算法的安全性和性能进行了深入的分析,包括直方图、相关系数、信息熵、密钥敏感度、密钥空间、差分攻击、加密效率等.实验结果表明,本文提出的图像加密算法具有优良的加密性能和安全性,可用于图像和视频通信的安全防范.
1 加密算法
由于该加密算法包括置换和扩散两个过程.故而在置换和扩散过程中使用斜帐篷映射.它是一个分段线性映射,其函数图像看起来像一个帐篷,定义为
(1)
式中:u∈[0,1]是状态变量,a∈(0,1)是系统参数.众所周知,斜帐篷映射具有很好的混沌特性[4].
1.1 置换过程
第1步.读取明文图像,得到一个二维矩阵P,大小为H×W,其元素值为0~255的整数.首先将明文图像分解为2个大小相同的子图像.将这2个子图像记为V1,V2,分别由P的左半部分和右半部分组成,设L=H×W/2.
第3步.根据式(2)生成基于明文图像内容的值p,用于生成明文相关的密钥流,以增强加密算法的安全性.
(2)

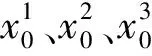

式中函数floor(x)返回小于或等于x的最大整数.
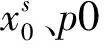
上述的置换过程具有3方面的优点:1)重新定位平面图像像素的位置,使得相邻像素之间的相关系数大大降低;2)由于密钥流与明文图像的内容相关,两个明文图像之间的细微差别会使置换后的图像产生极大的差异;3)该置换过程能有效抵抗已知/选择明文攻击、已知密文攻击和差分攻击.
1.2 扩散过程
在扩散过程,通过将明文图像像素的灰度值与斜帐篷映射生成的密钥流元素值混合,对像素值进行顺序修改,破坏密文图像与明文图像之间的关系.扩散过程以S形模式扫描实现,正常扩散过程与S型扩散过程的区别如图1和图2所示.假设两幅明文图像只有一个像素差别,该像素坐标为(x,y),经过置换后,假设位置(x,y)变换到(x′,y′),那么经过正常方向的扩散后,密文图像有差别的像素将从(x′,y′)开始一直到图像的末端,在(x′,y′)之前的像素的灰度值并没有改变.本文所提出的扩散过程采用图2所示的S形模式扫描实现,并且从最后一个像素开始进行扩散操作.由于置换后两幅图像的最后一个像素总是不同的,所以本文的扩散过程操作一轮后,最后一个像素的差别将扩散到整个图像.因此,S形模式扫描下的扩散过程可以显著提高加密算法的效率[13].详细的扩散过程描述如下:
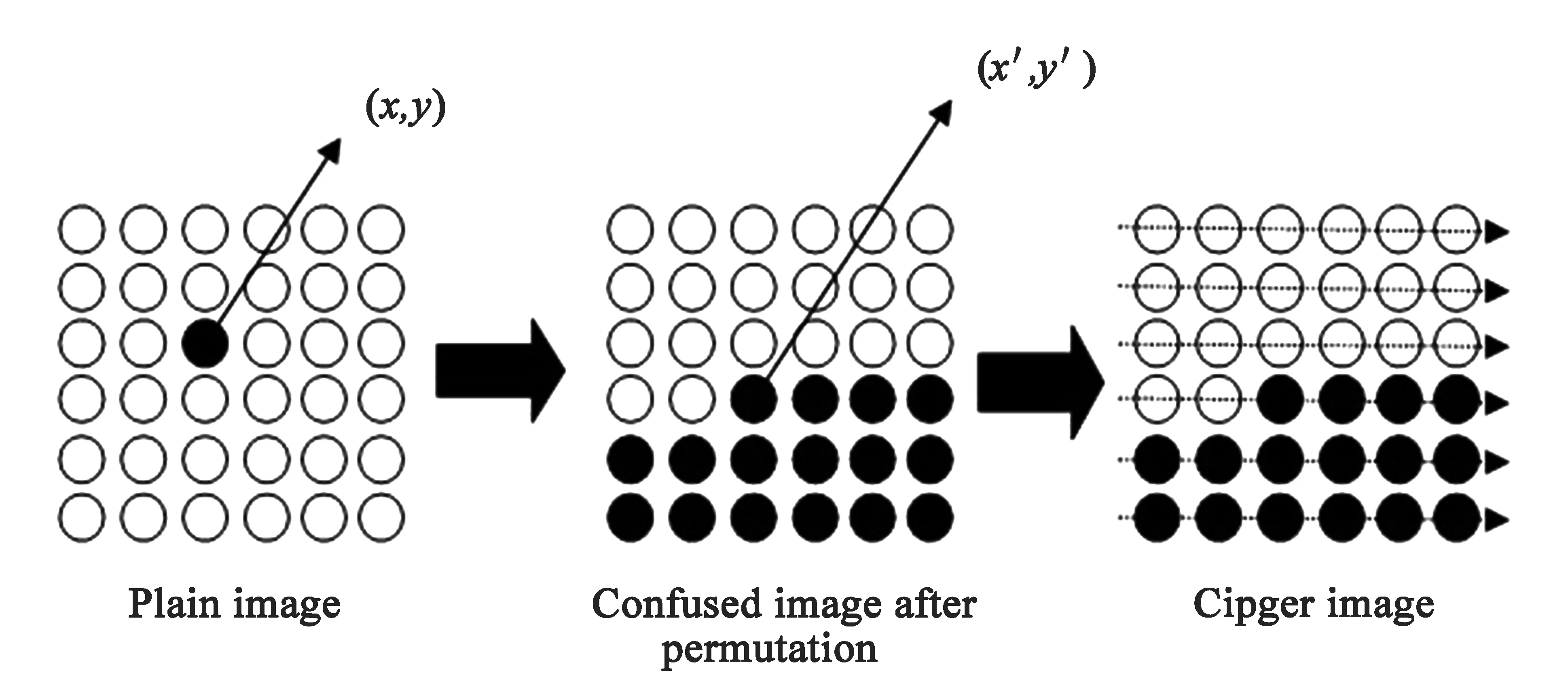
图1 正常置换-扩散模式

图2 S型置换-扩散模式
第1步.给定初始值x01、x02、x03, 控制参数a1和密钥q,p1.
第2步.分别使用初始值x01、x02、x03迭代斜帐篷映射q次, 去掉这些值以避免有害的过渡效应.为了简单起见,将得到的三个轨道点xq1、xq2、xq3分别表示为x01、x02、x03,令n=1.
第3步.计算t=mod(p1,3)+1.根据得到的t,计算下一个轨道点x1t=T(x0t,a1).并用式(3)计算密钥流元素
K1=floor(x1t×256).
(3)
第4步.使用式(4)屏蔽明文像素值,然后重置p1为生成的密文图像像素值
c(n)=K1⊕p(n)⊕c(n-1),
(4)
式中:运算“⊕”表示按位异或运算,p(n),K1,c(n)和c(n-1)分别表示当前明文图像像素、密钥流元素、输出密文图像像素和上一个密文图像像素.要加密第一个像素,必须将c(0)设置为种子.
第5步.n增加1并返回步骤3,直到完成所有像素的加密.最后将密文图像向量转换为一个二维矩阵,即得到最终的密文图像.
解密算法是加密算法的逆过程,略.
2 实验结果与分析
对所提出的加密算法、DSVSM[13]和算法1[14]进行了实验仿真和性能分析.DSVSM和算法1的密钥与文献[13]和[14]中的密钥相同.所有的模拟仿真均在一台配备Intel Xeon 2.13 GHz CPU,2 GB内存和300 GB硬盘空间的计算机上实现.计算机的操作系统是Windows 7 Professional,编译平台为matlab7.1,并用matlab7.1绘制了图形.
2.1 密钥空间分析

所以密钥空间足够大,足够抵抗暴力攻击.
2.2 直方图分析
图像直方图通过绘制每个灰度级的像素个数来显示图像中像素值的分布.有效的加密图像的理想直方图应该服从均匀分布,并且与明文图像的直方图有很大的不同.图3(a)、(b)分别为明文图和加密图,(c)、(d)分别为Lena及其密文图像的直方图.很明显,加密图像的直方图是均匀的,并且与明文图像的直方图有巨大的不同,这意味着加密后明文图像的冗余被成功地消除了,因此它不能为统计攻击提供任何有用的信息.

图3 加密结果
2.3 密钥敏感性分析
一个有效的加密算法应该对密钥具有很强的敏感性.为了测量算法对密钥参数K的敏感性,在其他参数不变的情况下对明文图像分别在K,K-Δδ和K+Δδ的情况下进行加密,相应的密文图像分别用I1、I2、I3表示.利用下式计算加密算法对参数K的敏感性.
(5)
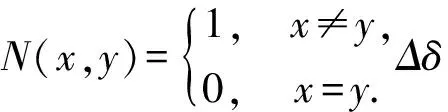

表1 密钥敏感性测试结果
参数Δδ的变化都是10-16.
表1表明所提出的加密算法对所有参数都非常敏感.敏感性测试也可以直观地观察,见图4,在保持其它参数不变的情况下,通过扰动x01=0.52后,对明文图像进行加密得到的2幅密文图像,具有99.64%的巨大差别;通过扰动x03=0.47后,对明文图像进行加密得到的2幅密文图像,具有99.61%的巨大差别.另一方面,用差别较小的密钥去解密原密钥加密的密文图像,也不能正确解密.

图4 密钥敏感性测试
2.4 相关性分析
一般来讲,自然有意义图像中相邻像素之间的相关性总是很高,因为它们的像素值非常接近,但是来自有效图像加密算法的密文图像中相邻像素之间的相关性应该足够低,以使统计攻击不可实行.从图像中随机选择N=5 000对相邻像素,根据公式(6)计算水平、垂直和对角线方向上相邻2个像素之间的相关性,其中xi和yi是随机选择的第i对像素.图5描绘了由所提出的加密算法产生的Lena及其密文图像的选定相邻像素的相关分布.表2~4分别给出了加密算法对3幅明文图像以及加密所生成的密文图像的相邻像素相关性的计算结果.图像和数据均表明,在明文图像中相邻像素之间的相关性很高,而在加密图像中,相邻像素之间的相关性被大大削弱,因此该加密算法具有很好的去除相邻相关性冗余的性能.

表2 本文算法、算法1和DSVSM生成的Lena密文图像的相邻像素相关系数

图5 相邻像素的相关性
(6)
(7)

表3 本文算法、算法1和DSVSM生成的Rice密文图像的相邻像素相关系数
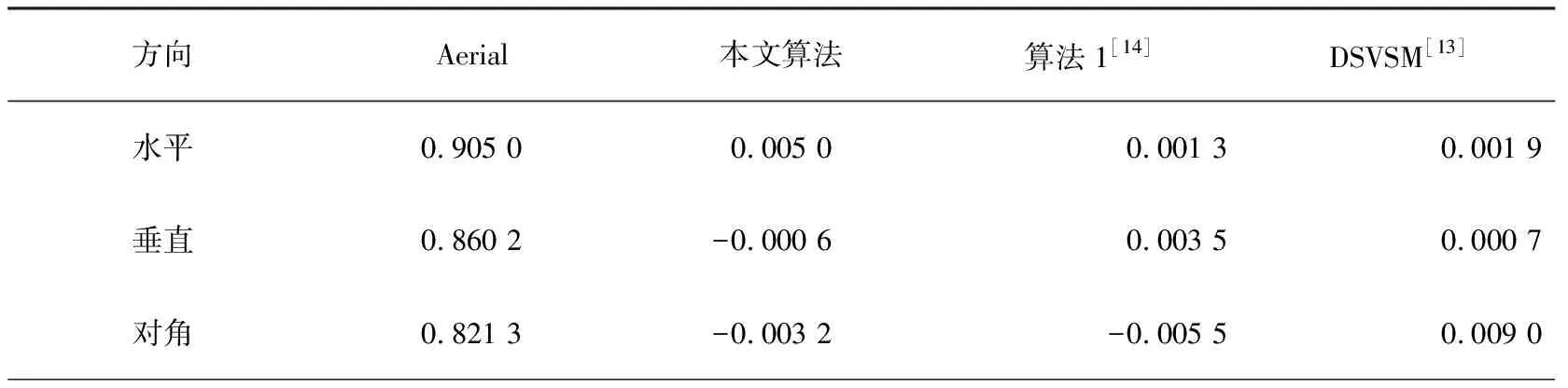
表4 本文算法、算法1和DSVSM生成的Aerial密文图像的相邻像素相关系数
引入了一个新的统计指标来反映密文图像的均匀性,即由公式(7)、(8)定义的共生直方图.水平方向的共生直方图由式(8)定义.
(8)
垂直方向的共生直方图由式(9)定义.
(9)
式中g(x,y)是图像所在位置(x,y)的像素值.如果g(x,y)=i,δ(g(x,y)-i)=1,否则δ(g(x,y)-i)=0.如果由式(10)定义的信息熵越大,共生直方图就越均匀.Lena与其密文图像的共生直方图如图6所示.从表5、6所示的3种不同方案产生的密文图像的共生直方图和信息熵,可以推断出本文的加密算法产生的密文图像在像素值分布上是均匀的.

表5 本文加密算法的共生直方图信息熵
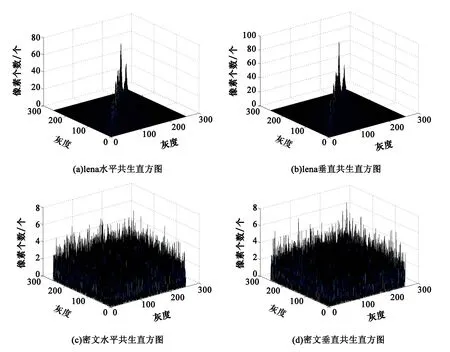
图6 Lena及其加密图像的共生直方图
(10)
式中:当i=1时,T=(H-1)×W;当i=2时,T=H×(W-1).

表6 对比算法的共生直方图信息熵
2.5 信息熵分析
信息熵是评价信息源随机性和不可预测性的标准之一[21].消息源的熵定义为
(11)
式中:s是信息源,T是表示所有符号si所需要的比特数,P(si)是符号si的概率.对于由2T符号组成的真正的随机信息源,其信息熵是T.因此,对于一个有效的加密算法,256灰度级的加密图像的信息熵应该接近8.否则,信息源的随机性不够强,存在一定的可预测性,使得加密算法不安全.由本文所提出的加密方案,算法1和DSVSM对5幅明文图像进行加密,所生成的密文图像的信息熵如表7所示.结果表明,本文所提出的加密算法所产生的密文图像的熵更接近于8,这意味着加密过程中的信息泄漏可以忽略不计,并且具有足够的鲁棒性来抵抗熵攻击.
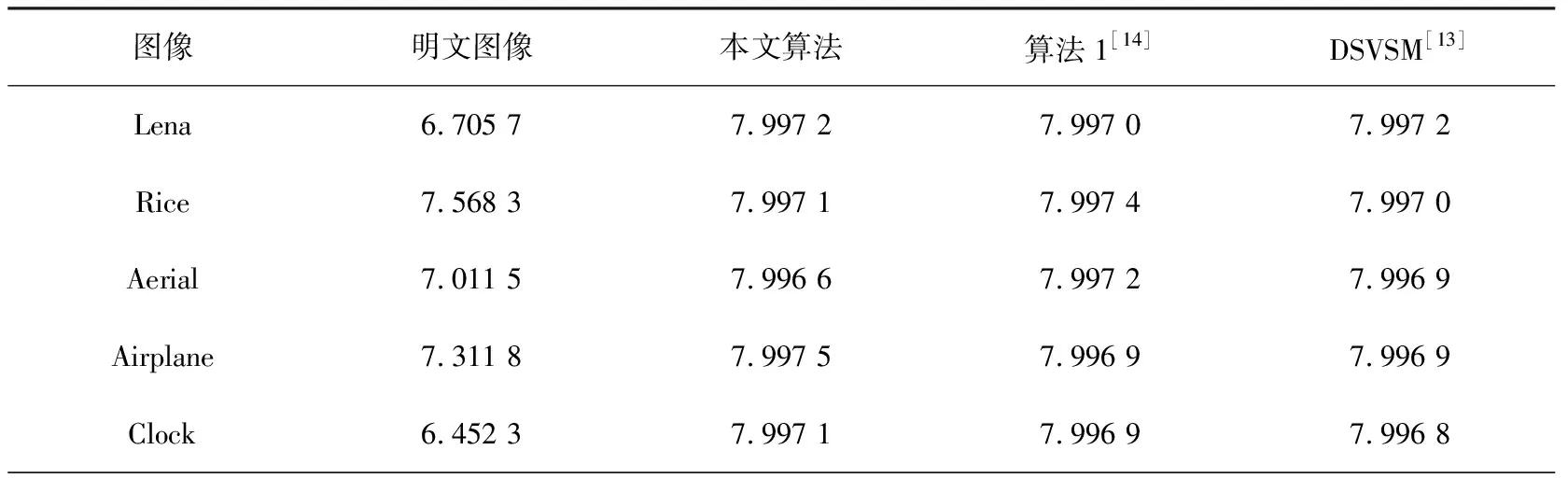
表7 本文算法、算法1和DSVSM产生的一轮加密图像的信息熵
2.6 差分攻击分析
为了抵抗差分攻击,明文图像中的细微差别应该会导致密文图像的巨大差别.利用像素变化率(NPCR)和统一平均变化强度(UACI)2个指标来衡量明文图像中一个像素变化对加密图像的影响.为了计算NPCR和UACI,假设2幅明文图像I1和I2在一个像素上相差一个灰度级,用相同的密钥加密得到密文图像分别表示为C1和C2.创建一个矩阵D,当C1(i,j)=C2(i,j)时,D(i,j)=0; 否则D(i,j)=1.NPCR和UACI按式(12)和式(13)计算.
(12)
(13)
在实验中,采用明文图像Rice,随机选择100个像素点,做100次加密,每一次加密改变一个像素的像素值,改变量为1个灰度级.然后比较2个密文图像来计算NPCR和UACI,取平均值,得到的结果见表8和表9.从表8和表9的结果可以看出,在一轮加密中,本文加密算法所得到的NPCR和UACI分别达到99.6%和33.4%左右, 接近NPCR和UACI的数学期望值99.609 4%和33.463 5%[8].结果表明,该加密方案在抵抗差分攻击方面,与算法1和DSVSM相比,具有更好的性能.
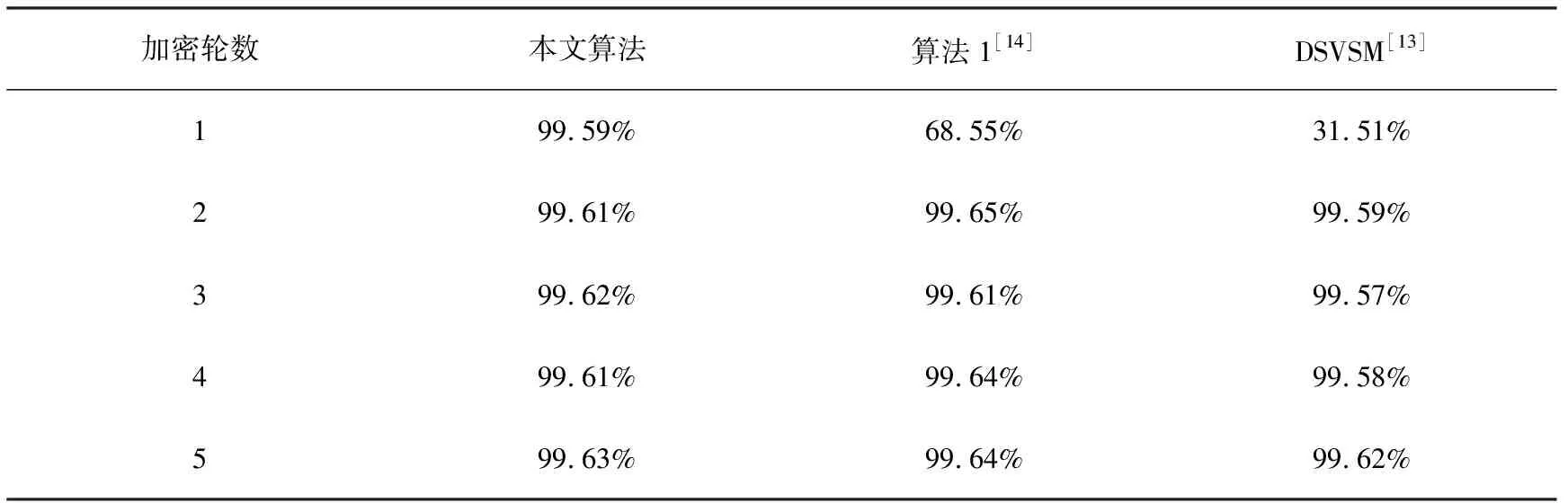
表8 NPCR性能测试

表9 UACI性能测试
2.7 速度分析
为了比较速度性能,对5张大小相同的测试图像进行加密,然后用每个加密方案和解密方案进行一轮加密解密,每个加密方案和解密方案所需的平均时间见表10.从表10中的数据可以看出,加密时间和解密时间都比2种对比方案短,因此本加密方案具有更好的速度性能.

表10 速度性能测试 单位:s
3 结论
本文提出了一种基于混沌映射和像素交换的图像加密方案,从3个方面较好地解决了经典置换-扩散结构的图像加密方案存在的缺陷.1)交换像素的位置由倾斜帐篷映射生成,与明文图像像素灰度值高度相关.因此,即使使用相同的密钥,对于不同的明文图像也可以得到不同的密钥流,并且该方案在抵抗已知/选择明文攻击和选择密文攻击方面具有很强的鲁棒性.2)众所周知,扩散过程是整个加密方案中代价最高的.基于像素交换的置换方法可以同时产生置换和扩散效应,从而加快加密速度.3)扩散过程以S形模式进行,只要实施一轮扩散,足以获得有效的扩散效果.对该加密算法的安全性和性能进行了深入的分析,结果表明本文提出的图像加密方案具有优良的加密性能和安全性,适用于图像和视频通信的安全应用领域.

