温度对系杆拱桥拱肋和系杆自振频率的影响★

刘兴国，陶成云，黄 巍

(1.哈尔滨学院土木建筑工程学院，黑龙江 哈尔滨 150086；2.黑龙江省地下工程技术重点实验室，黑龙江 哈尔滨 150086)

0 引言

自振频率是桥梁领域常用的参数，但测试得到的自振频率会因外界环境改变而产生一定变化。其中，温度是导致桥梁结构自振频率发生变异的主要因素之一。多次超静定系杆拱桥兼有连续梁桥与拱桥的受力特点，并存在结构体系转变，所以受温度影响更加严重。目前，温度对此类复杂桥梁结构自振频率的影响机理和规律等方面还没有得到确定的结论，因此开展桥梁结构自振频率的温度效应分析十分必要[1-4]。

本文通过现场试验测试和有限元模拟，对自振频率进行深入分析，并依据实测数据建立大气温度与结构自振频率间的函数关系，对环境温度影响的结构自振频率进行有效预测。

1 依托工程概况及其温度试验研究

1.1 工程概况

本文以齐齐哈尔某下承式三跨预应力混凝土系杆拱桥为依托，该地区有记录以来，年平均气温在3.2 ℃左右，1月均温-25.7 ℃，日最低气温-33.7 ℃；7月均温22.8 ℃，日最高气温34.8 ℃。

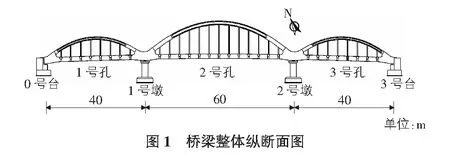
桥梁跨径布置为40 m+60 m+40 m的刚性系杆刚性拱，拱轴线采用二次抛物线。拱肋均采用工字形等截面，为钢筋混凝土结构；系杆采用箱型截面，直线段处系杆高1.8 m，宽1.4 m。桥梁总体纵向布置图如图1所示。

1.2 结构振动测点布置及测试时段

1)测点布置。

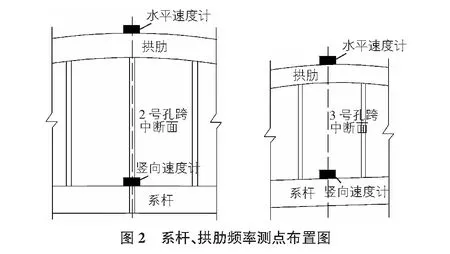
选取2号和3号孔跨中断面作为拱肋及系杆自振频率的测试控制断面，并在拱顶每个测试位置放置一个水平速度计，系杆每个测点布设一个竖向速度计。各结构振动测点布置如图2所示，现场测点布置如图3所示。

2)测试时段。

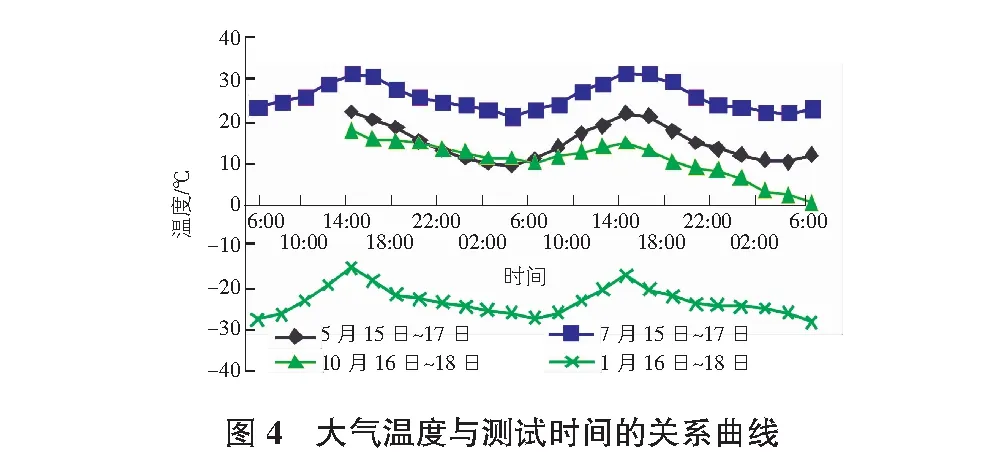
依据当地气象资料及天气预报选取一年四季中具有代表性的时段内，每2 h对环境温度及结构振动进行连续测试。测试过程中对桥梁进行临时封闭，测试时段内环境温度在-28.3 ℃～31.5 ℃。测试时段内大气温度与时间关系曲线如图4所示。

1.3 实测结构自振频率数据分析

环境温度作用下测试时间与结构自振频率的变化曲线如图5所示。

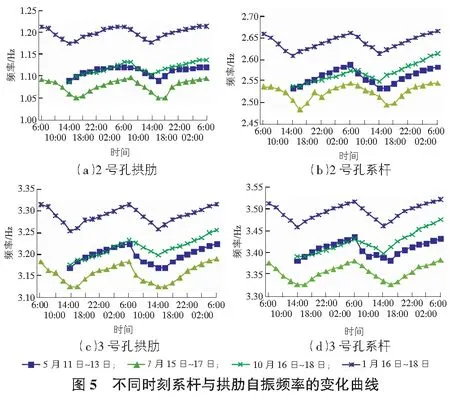
由图5可知，在温度影响下，实测系杆及拱肋自振频率与日温度、季节性温度均总体呈负相关性；同时结构频率与日温差及季节性温差幅度均呈现出正比关系，即温差越大其自振频率变化量也随之增大，反之亦然。

此外，实测月频率变化量与总频率变化量均表现出温度对该桥低阶频率影响明显。

1.4 实测系杆竖向温度梯度模式的研究

根据试验数据可得，沿结构高度方向在结构测点温度最低点作为基准温度[5-6]。将每个时刻各测点温度与基准温度作差后作为结构温度梯度。其中系杆选取距顶缘0.8 m处，拱肋选取距顶缘0.85 m处作为基准温度点。系杆及拱肋竖向测点的相对温差分布曲线如图6所示。

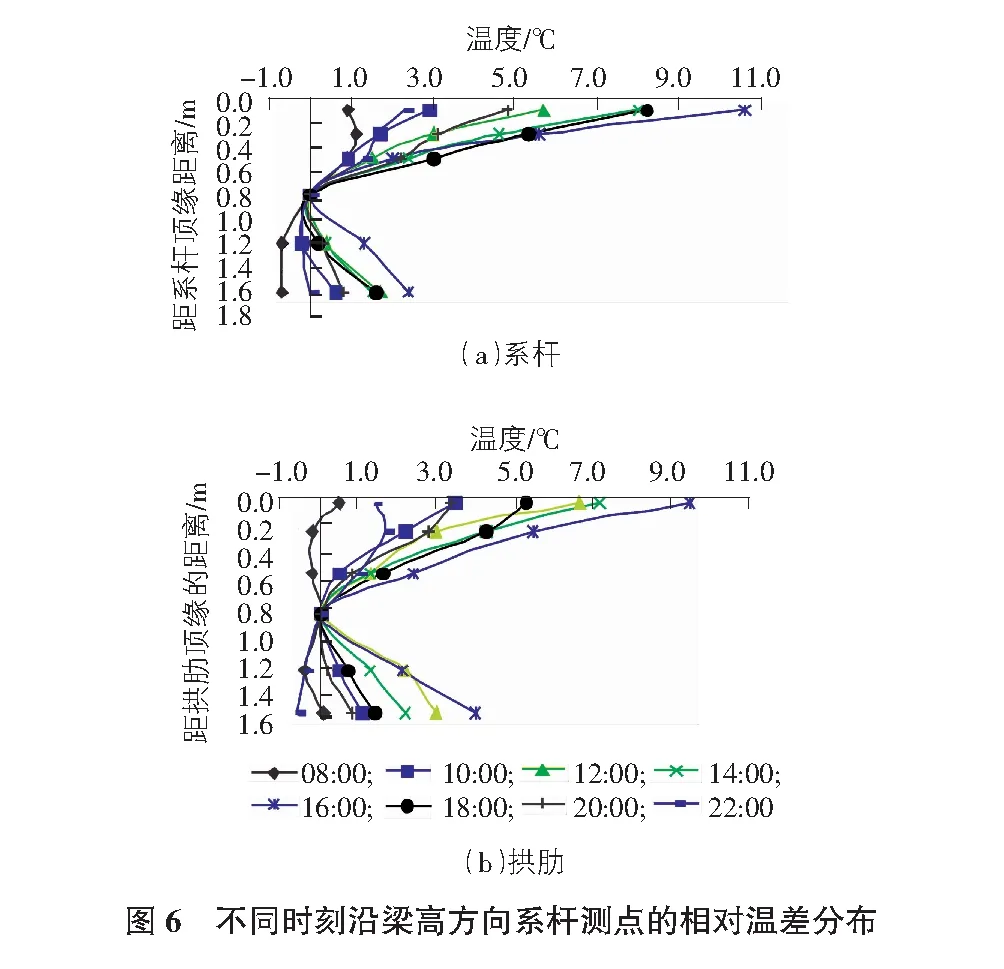
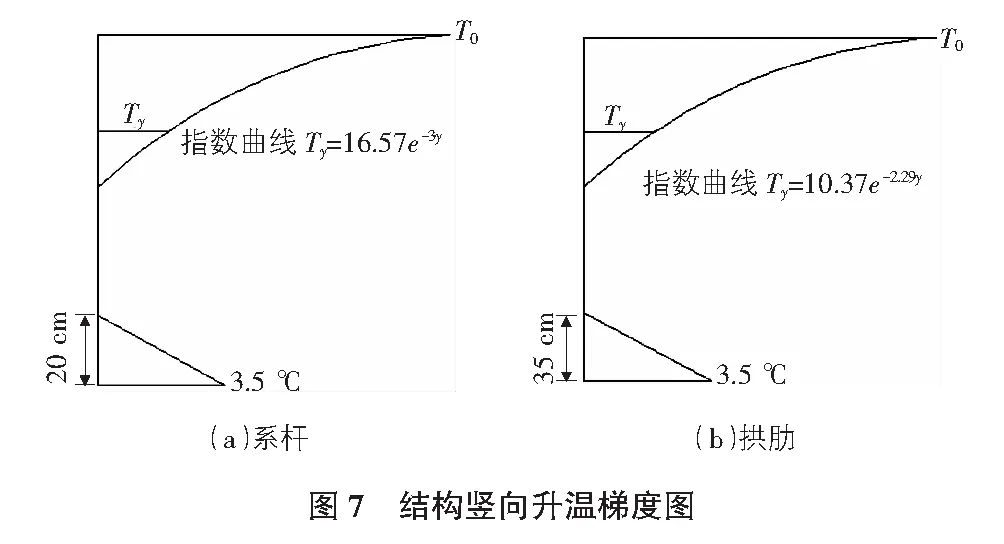
参照文献[7]，距系杆顶缘0.8 m及拱肋顶缘0.85 m范围内，以指数函数拟合此时刻的结构竖向温度梯度表达式分别为Ty=14.58e-3.19y和Ty=10.89e-2.73y。为使所研究的结构竖向温度梯度更符合实际，根据我国公路桥梁规范中规定温度梯度的取值方法，又选取2020年1月16日～18日，6月10日～12日，7月15日～17日及8月12日～14日进行竖向测点温度的连续测量后拟合得到系杆及拱肋竖向温度梯度拟合公式分别为Ty=16.57e-3y和Ty=10.37e-2.29y。

由距系杆顶0.8 m及拱肋顶0.85 m外温度的观测可知，其温差均在3.5 ℃以内，故参考其他资料及美国规范的规定[8-9]，本文所取的系杆及拱肋升温梯度如图7所示。

1.5 竖向温度梯度的有效性验证

选取第2年6月5日～8日实测温度与拟合公式计算值进行对比，结果见表1，表2。可知，在日最高温度时系杆实测与计算值最大相差0.25 ℃，最大误差率为3.42%；拱肋实测与计算值最大相差0.36 ℃，误差率为6.55%，说明本文拟合的系杆及拱肋竖向温度梯度公式具有较好的准确性。

系杆及拱肋竖向温度梯度可等效为各测点温度如式(1)，式(2)所示:

系杆：

(1)

拱肋：

(2)

其中，T(y)为各点的温差值，是坐标y的函数，℃；y为该点距系杆上缘的距离，m。

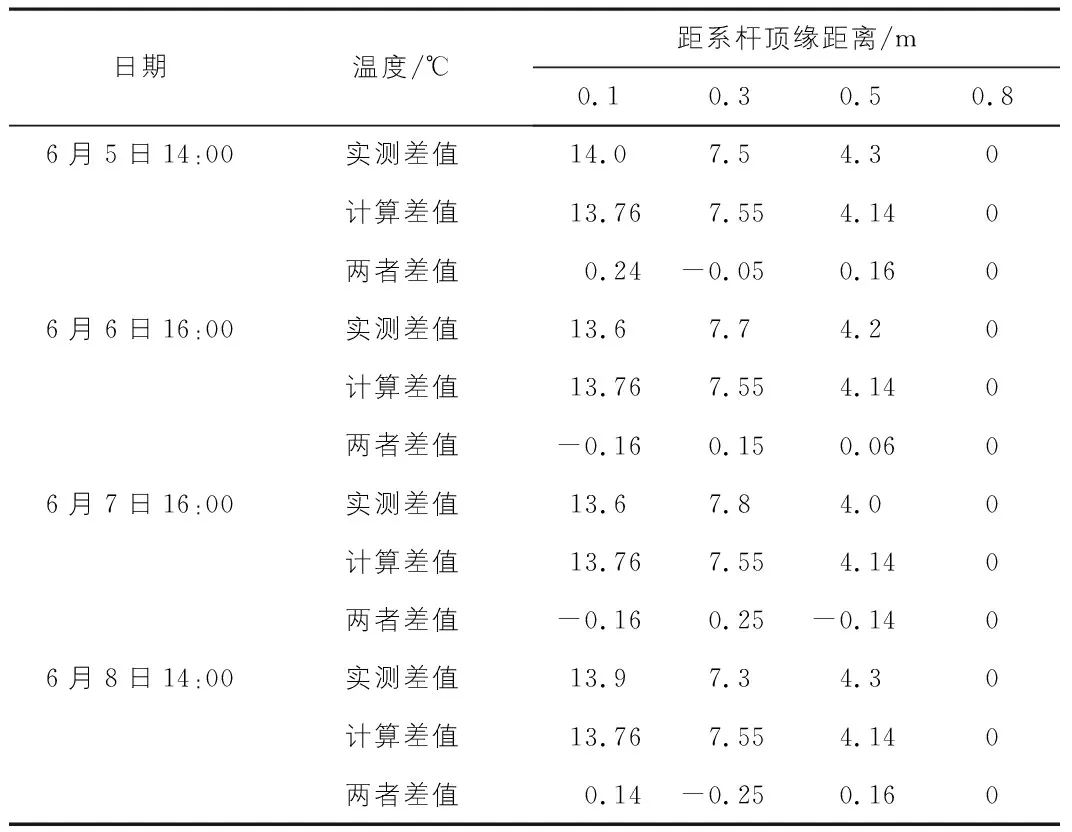
表1 实测与计算相对温度差的比较

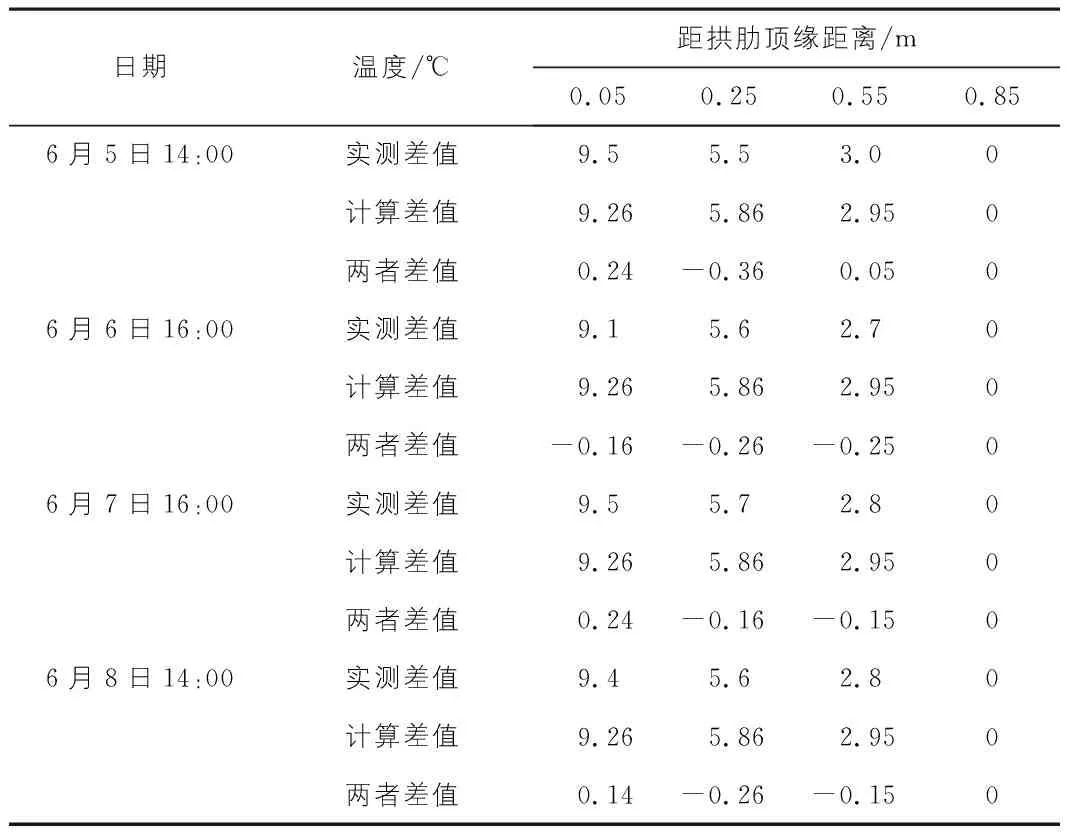
表2 实测与计算温度比较结果

2 自振频率有限元模型建立

由于温度主要通过影响结构材料的弹性模量和胀缩而影响其振动，且当温度在10 ℃～65 ℃范围内，混凝土热膨胀系数几乎不变，温度引起结构尺寸变化的影响可以忽略不计。因此，本文主要针对温度变化所引起材料弹性模量的改变建模分析温度对此类桥梁结构动力特性的影响规律及程度。

2.1 温度与材料弹性模量的本构关系

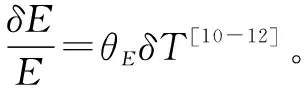
2.2 模型的建立及分析

采用Midas建立系杆拱桥上部结构空间有限元模型时，系杆、横梁及拱肋均采用空间梁单元模拟；吊杆采用桁架单元模拟。模拟吊杆时，假定吊杆在系杆及拱肋上锚固位置固结，无相对滑移。为保证计算结果的准确性，拱脚处采用实体单元。根据桥梁成桥后支座的实际状况，并按支座实际刚度进行模拟。采用子空间迭代法，分析该桥的频率及振型，在分析模型中，温度荷载采用梁截面温度加载方式。此模型忽略结构尺寸的变形影响，不考虑车辆等外界荷载的作用，各结构材料均为各向同性，且在整个受力过程中始终处于弹性工作状态。该桥有限元模型如图8所示。

本文在对桥梁结构频率受温度效应影响时主要考虑以下三种温度形式：整体温度的影响分析(选取整体温度范围在[-30 ℃，30 ℃]之间，以5 ℃为温度间隔)；拱梁温差的影响分析(系杆温度不变，单独改变拱肋温度时对结构自振频率的影响)；温度梯度的影响分析。针对拱肋竖向温差、系杆竖向温差及拱肋、系杆竖向温差的共同作用这三种温度方式进行分析，其结构竖向温度梯度荷载的取值见上节，并满足温度与混凝土材料的本构关系。

2.3 模型的修正

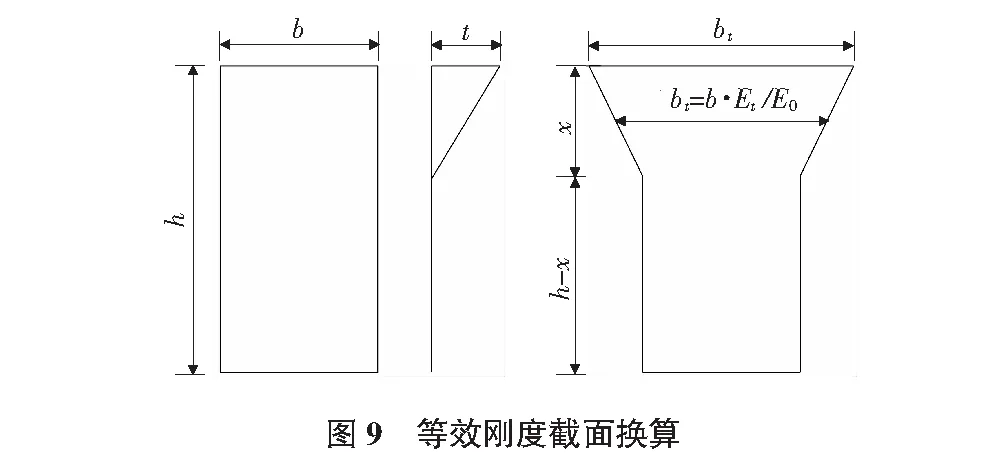
在分析温度梯度时，采用等刚度原理，如图9所示，在实心矩形混凝土截面顶部X范围内存在梯度温度，设混凝土弹性模量随温度的变化性质为Et=k·E0。在截面梯度温度作用下，为使用梁单元进行结构分析又考虑不同高度处混凝土弹性模量变化程度的不同，在统一截面上的弹性模量的基础上，考虑将梯度温度影响范围内的截面宽度进行加宽，增加比例为bt=k×b=b×Et/E0，然后计算等效后的截面性质It，At，仍以原弹性模量E0代入模型，重新分析结构的频率和振型。

3 考虑温度影响的自振频率分析

3.1 整体温度对自振频率的影响

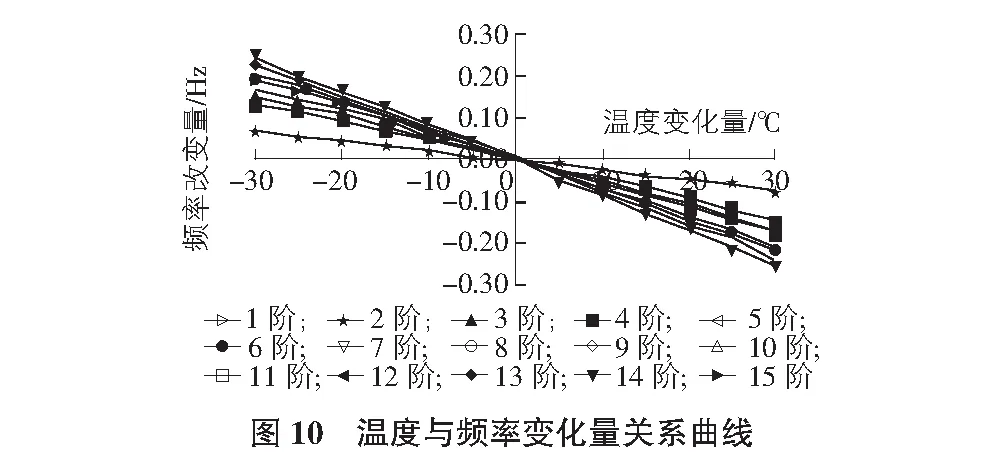
在忽略结构阻尼影响的情况下，桥梁自振特性主要由结构刚度矩阵或质量矩阵决定[13]。温度正是通过影响其材料性能中的弹性模量，进而改变结构的刚度矩阵，以达到对结构振动的影响。计算整体温度变化与频率变化量关系曲线如图10所示。整体温度改变对结构自振频率的影响表现出以下特点：

1)系杆拱桥自振频率的变化规律与温度的变化规律呈负相关关系；且在逐渐升降温过程中，温度变化引起系杆竖向弯曲振动频率的变化率相对较小，而对拱肋振动频率变化的影响相对较大。

2)升降温各30 ℃范围内，前15阶频率变化率在-7.01%～6.55%，说明整体温度变化对系杆拱桥自振频率的影响较大；频率总减小量达13.56%，温度变化量与频率变化量近似呈线性关系。

3)整体升降温度变化相同时，升温对结构频率的影响略大于降温的影响。

3.2 拱梁温差对自振频率的影响

系杆拱桥存在拱梁温差和索梁温差，但索梁温差对桥梁频率的影响极小，可忽略不计[14]。由于拱肋与系杆所处空间位置不同，且两侧外悬臂对系杆有一定遮挡作用，故在分析拱梁温差影响时，为简化计算，假定拱脚80%混凝土及所有横梁均被遮挡，且拱脚混凝土及横梁混凝土温度始终与系杆温度保持一致。

分析时保持系杆温度不变，拱梁混凝土内部平均温度差值以现场测试的[-4 ℃～6 ℃]为区间，以2 ℃为变化间隔。拱梁温差与频率变化量的关系曲线如图11所示。由图11可知，前15阶频率变化率在-1.49%～0.9%之间，即其对结构自振频率影响很小，频率变化量与温度变化量近似呈线性关系。

3.3 温度梯度对自振频率的影响

由模型分析结果可得，在不同竖向升温温度梯度作用下，系杆拱桥前15阶自振频率的变化量及变化率结果见表3。由表3中的数据可知：

1)单结构竖向温度梯度影响时，拱肋竖向温度梯度对系杆拱桥频率的影响大于系杆竖向温度梯度的影响。

2)共同竖向温度梯度作用下，结构频率最大变化量为0.053 Hz，变化率为1.68%，即竖向温度梯度对系杆拱桥自振频率的影响非常小。

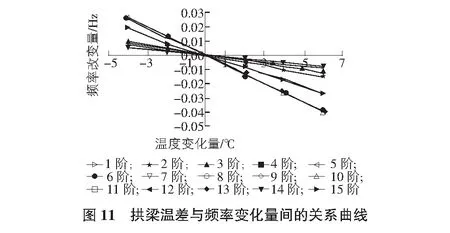
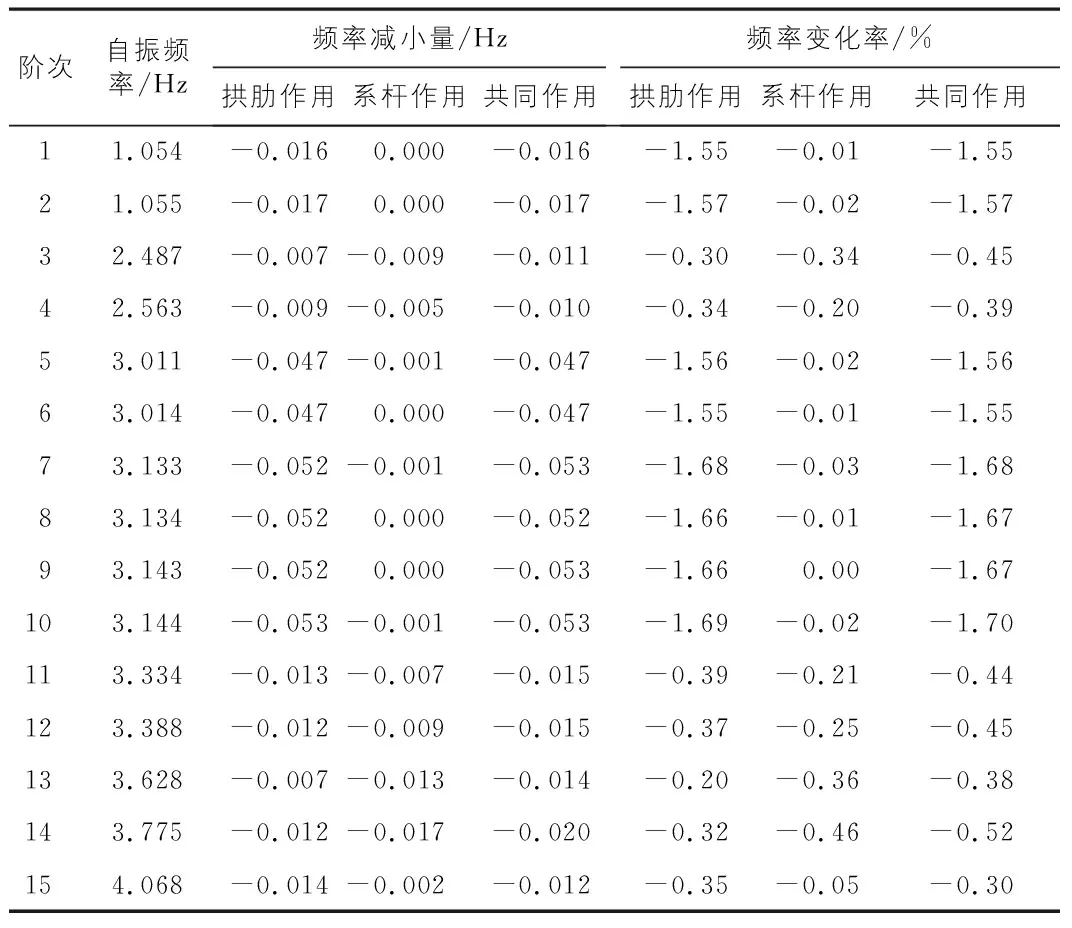
表3 不同竖向温度梯度作用下频率影响的比较

综上所述，上述三种温度模式中，整体温度变化对系杆拱桥频率的影响最大，而拱梁温差及竖向温度梯度引起的影响则要小得多，在设计中需对整体温度的影响进行考虑。

4 BP神经网络算法及实际工程验证

根据之前温度与频率的实测数据进行统计分析，采用偏相关分析方法[15-16]，基于LM-BP神经网络，建立拱肋、系杆自振频率与大气温度的回归模型。现场共测试了117组试验数据，其中前92组数据作为训练样本数据，后25组作为对比评估数据。

由现场实测数据及有限元分析结果可以看出，温度与频率两者以线性相关为主，故采用SPSS软件的逐步回归分析方法，并使回归系数满足在95%置信区间范围内，对大气温度与结构频率的实测数据进行线性分析，回归系数及相关性结果见表4。

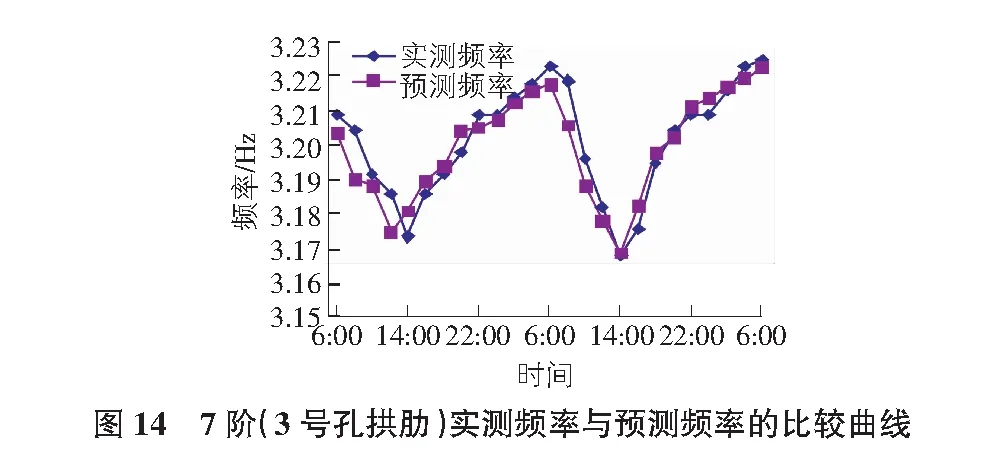
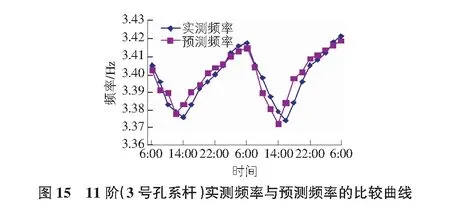
根据表4的回归系数，对后25组的实测频率值与预测频率值进行对比，对比结果如图12～图15所示。系杆、拱肋实测频率与预测频率最大误差率分别为0.69%和0.43%，说明此频率预测模型可对系杆拱桥结构自振频率进行有效的预测。

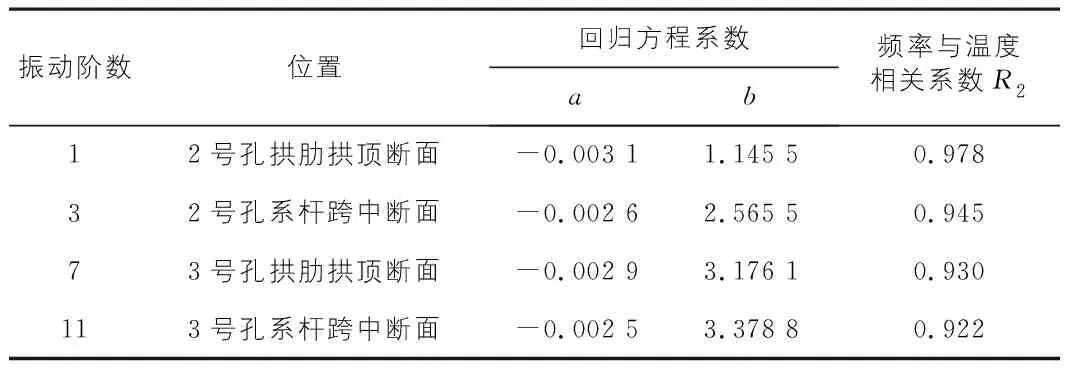
表4 频率与温度线性回归结果

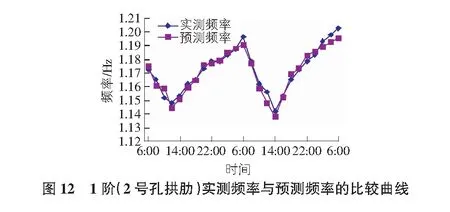
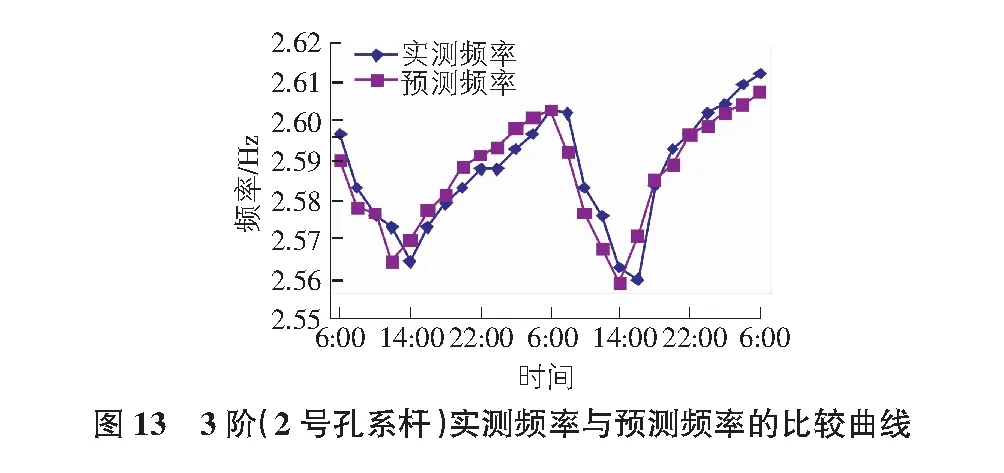
5 结论

本文基于系杆拱桥通过现场试验与有限元模型分析，对温度变化引起结构自振频率的变化规律及程度进行了研究，并采用BP神经网络算法对桥梁结构自振频率进行预测。得出结论如下：

1)温度变化对系杆拱桥自振频率的影响随振动阶数的增加，逐渐变小。温度与频率间的变化规律呈负相关，且两者变化量近似呈线性关系。

2)基于温度与材料弹性模量间的本构关系，分析得出在[-30 ℃,30 ℃]范围内的整体温度对结构频率影响最大变化率达13.56%，而拱梁温差及竖向温度梯度的影响则小得多，所以设计中应考虑整体温度的影响。

3)LM-BP神经网络算法对系杆及拱肋自振频率进行预测，最大误差率分别为0.69%和0.43%，说明此预测模型可对结构自振频率进行有效的预测。