Stable Label-Specific Features Generation for Multi-Label Learning via Mixture-Based Clustering Ensemble

Yi-Bo Wang, Jun-Yi Hang, and Min-Ling Zhang,,

Abstract—Multi-label learning deals with objects associated with multiple class labels, and aims to induce a predictive model which can assign a set of relevant class labels for an unseen instance. Since each class might possess its own characteristics,the strategy of extracting label-specific features has been widely employed to improve the discrimination process in multi-label learning, where the predictive model is induced based on tailored features specific to each class label instead of the identical instance representations. As a representative approach, LIFT generates label-specific features by conducting clustering analysis. However,its performance may be degraded due to the inherent instability of the single clustering algorithm. To improve this, a novel multilabel learning approach named SENCE (stable label-Specific features gENeration for multi-label learning via mixture-based Clustering Ensemble) is proposed, which stabilizes the generation process of label-specific features via clustering ensemble techniques. Specifically, more stable clustering results are obtained by firstly augmenting the original instance representation with cluster assignments from base clusters and then fitting a mixture model via the expectation-maximization (EM)algorithm. Extensive experiments on eighteen benchmark data sets show that SENCE performs better than LIFT and other wellestablished multi-label learning algorithms.

I. INTRODUCTION

MULTI-LABEL learning aims to build classification models for objects assigned with multiple semantics simultaneously, where each example is represented by a single instance and a set of relevant class labels [1]. As multi-label objects widely exist in the real world, multi-label learning has diverse applications, such as text categorization [2], image annotation [3], web mining [4], and bioinformatics analysis[5], etc.

In recent years, a significant amount of algorithms have been proposed for multi-label learning. One common strategy adopted by most existing approaches is to build a predictive model based on the identical instance representations for each class label [1]. However, this strategy might be suboptimal as each class label is supposed to have distinct characteristics of its own. For instance, in text categorization, features corresponding to the word terms voting, reform and government would be informative in discriminating political and non-political documents, while features related to the word terms piano, Mozart and sonata would be informative in discriminating musical and non-musical documents. Therefore, the strategy of label-specific features [6] has been proposed to benefit the discrimination of different class labels.

As a representative approach for label-specific features,LIFT [6] utilizes clustering techniques to investigate the underlying properties of the feature space for each class label.Nevertheless, the clustering in LIFT tends to be unstable due to the inherent instability of the single clustering method [7].To address this, clustering ensemble techniques [8]–[10] can be utilized to obtain clustering results with stronger stability and robustness. With the assumption that the clustering results of related labels should be similar, LIFTACE [8] employs clustering ensemble techniques to integrate the preliminary clustering results of all class labels based on the consensus similarity matrix. However, it fails to utilize the information embodied in the original data representation during the combination process of clustering ensemble.

To address aforementioned issues, a novel approach named SENCE, i.e., stable label-Specific features gENeration for multi-label learning via mixture-based Clustering Ensemble,is proposed, which stabilizes the clustering process via a twostage method. Firstly, several base clusters are exploited to conduct clustering analysis on positive and negative instances of each class label. Then, base cluster assignments are combined via a tailored expectation-maximization (EM)procedure, where a mixture model is fitted on clusteringaugmented instances. After that, a predictive model is induced based on the label-specific features derived from the improved generation strategy.

In this paper, we advance the label-specific feature generation via a novel clustering combination strategy, which is an essential step in clustering ensemble. The novel strategy can fully leverage the information hidden in the original data representation and encoded in each cluster assignment to avoid suboptimal results of existing techniques. Comprehensive experiments over 18 benchmark data sets indicate the effectiveness of SENCE.

The rest of this paper is organized as follows. Section II briefly reviews related works on multi-label learning. Section III presents the proposed approach SENCE. Section IV reports the experimental results on 18 benchmark datasets. Finally,Section V concludes.

II. RELATED WORKS

The task of multi-label learning has been extensively studied in recent years. Generally, the major challenge for multi-label learning is its huge output space which is exponentially related to the number of class labels. Therefore,exploiting label correlations is regarded as a common strategy to facilitate the learning process. Roughly speaking, existing approaches can be grouped into three categories based on the order of correlations [1], [11], i.e., first-order approaches,second-order approaches and high-order approaches. Firstorder approaches tackle multi-label learning problem in a label-by-label manner [3], [12]. Second-order approaches exploit pairwise relationships between class labels [13], [14].High-order approaches exploit relationships among a subset of class labels or all class labels [15]–[17].

In addition to exploiting label correlations in the output space, another strategy for facilitating multi-label learning is to manipulate the input space. The most straightforward feature manipulation strategy is to conduct dimensionality reduction [18]–[20] or feature selection [21]–[24], which is also a common strategy used in multi-class learning, over the original feature space. Besides, there are also some other methods, such as generating meta-level features [25], [26]with strong discriminative information from the original representation, constructing multi-view representations for multi-label data [27]–[29], etc. Note that all these feature manipulation strategies employ identical feature representation for all labels in the discrimination process.

Instead, label-specific feature generation serves as an alternative feature manipulation strategy, which extracts the most discriminative features for each individual label. Some works generate label-specific features by selecting a different subset of the original features for each class label [30]–[33].Based on the sparse assumption, the most pertinent and discriminative features for each label can be identified using spectral clustering and least absolute shrinkage and selection operator (LASSO) algorithms [34].

In addition to conducting label-specific feature selection in the original feature space, it is also feasible to derive labelspecific features from a transformed feature space. For example, LIFT [6] performs clustering analysis on the positive and negative instances of each class label, and generates labelspecific features by querying the distances between the instance and the clustering centers. To improve this, attribute reduction [35] can be employed in the process of label-specific features construction to remove redundant information in generated label-specific features. Some other works aim to enrich label-specific features by exploiting the nearest neighbor rule [36], exploring spatial topology structures [37],jointly considering label-specific features generation and classification model induction [38], generating BiLabelspecific features based on heuristic prototype selection and embedding [39], or imposing structured sparsity regularization over the label-specific features [40].

Recently, clustering ensemble techniques have been considered to enhance the process of label-specific feature generation. However, off-the-shelf clustering ensemble techniques employed in previous methods fail to utilize the information embodied in the original data representation [8],[41]. In this paper, we propose a novel clustering ensemble strategy for label-specific feature generation, where the information hidden in the original data representation and encoded in each cluster assignment is taken into consideration simultaneously to facilitate the generation of more stable clustering. We will detail our approach in the next section.

III. THE PROPOSED APPROACH

A. Preliminaries

Formally, let X=Rddenote thed-dimensional input space and у={l1,l2,...,lq} denote the label space includingqclass labels. Given the multi-label training set D={(xi,Yi)|1 ≤i≤m} wherexi=[xi1,xi2,...,xid]T∈X is thed-dimensional feature vector andYi⊆у is the set of relevant labels associated withxi, the task of multi-label learning is to induce a predictive modelh:X →2уfrom D which can assign a set of relevant labelsh(u)⊆у for an unseen instanceu∈X.Specifically, LIFT learns from D by taking two steps, i.e.,label-specific features construction and predictive model induction.

In the first step, for each class labellk∈у, instances are divided into positive set and negative set as follows:

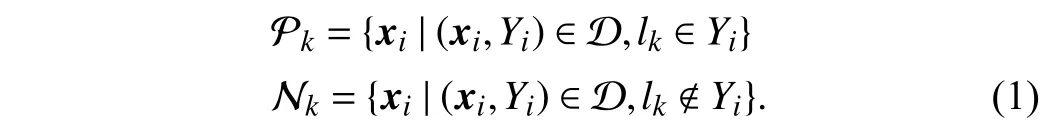
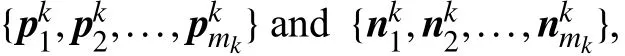
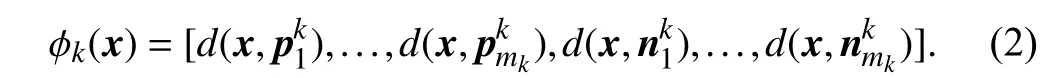
Here,d(·,·) returns the Euclidean distance between two feature vectors.

In the second step, a new binary training set Bkis constructed from the original training set D according to the label-specific features generated by the mappingϕk

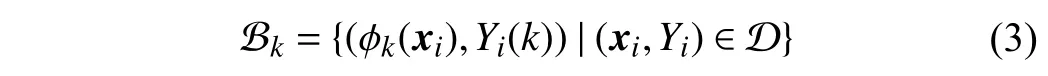
whereYi(k)=+1 iflk∈YiandYi(k)=−1 otherwise. Based on Bk, a classification modelgk:Zk→R forlkis induced by invoking any binary learner L. Given an unseen instanceu∈X, its relevant label set is predicted as

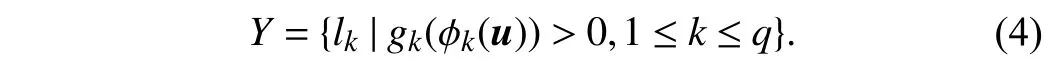
B. SENCE

SENCE learns from D by taking four elementary stages,which aims to induce a multi-label classification model with the generated label-specific features. The first two stages are designed to stabilize the clustering process via clustering ensemble techniques. Specifically, the first stage augments the original instance representations based on cluster assignments from base clusters. The second stage fits a mixture model on augmented instances via the EM algorithm to obtain more stable clustering results. The third stage constructs labelspecific features, and the fourth stage induces predictive models, which are consistent with the corresponding stages in LIFT. To facilitate understanding, the notations set in SENCE are summarized in Table I.

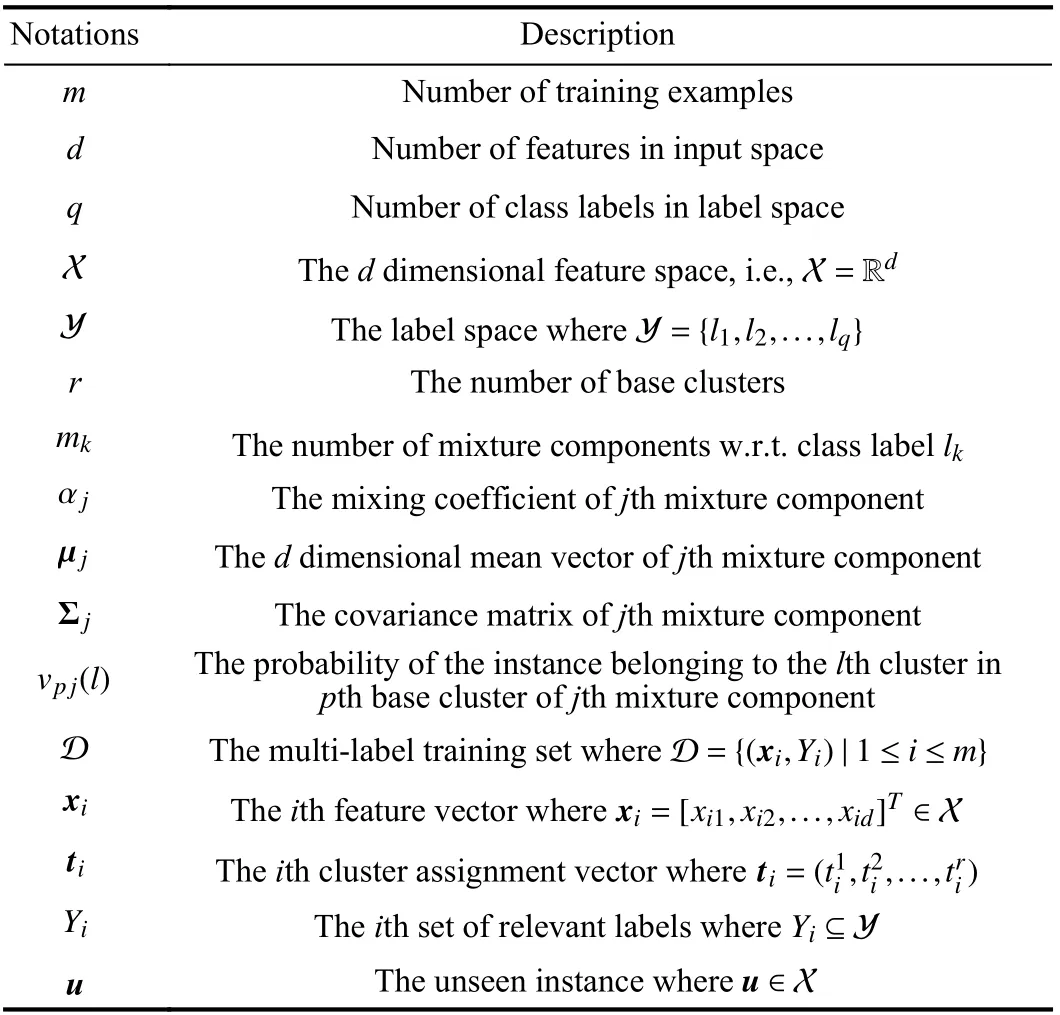
TABLE I THE SET OF NOTATIONS FOR SENCE

1)Clustering-Based Feature Augmentation:For each class labellk, SENCE divides instances into the positive set and negative set donated as Pkand Nkrespectively according to(1). To mitigate the inherent instability of the single clustering method, in contrast to LIFT, SENCE employs multiple base clusters on Pkand Nkto derive cluster assignments and rerepresents Pkand Nkas follows:

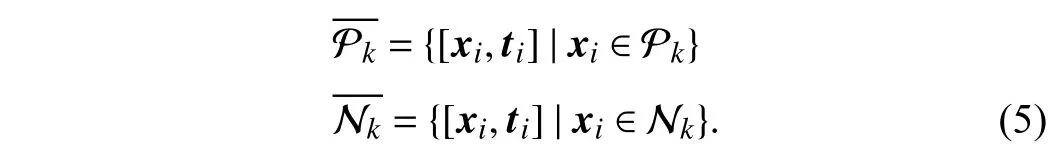
Here,ti=()is a clusterassignmentvector,whereristhe number ofbaseclusters andthepthelementindicates the cluster assignment given by thepth base cluster. The cluster assignment vectortiis regarded as extra features to augment the original instancexi. Thus, such feature representation of instances inandcan fully encode the information embodied in the original data representation and the cluster assignments, which makes the following labelspecific feature extraction more stable and robust.

2)Clustering Combination via A Mixture Model:Existing clustering ensemble methods work in two steps, i.e., clustering generation and clustering combination. In the clustering generation step, similar to existing clustering ensemble methods, SENCE exploits several base clusters to conduct clustering analysis on positive and negative instances of each class label. As the original features and the augmented features are generated in different ways, existing clustering combination methods might be suboptimal. Thus, in the clustering combination step, instead of directly combining base cluster assignments as existing clustering ensemble methods do, SENCE innovatively performs another clustering analysis on augmented instances which treat the original features and the augmented features in different ways. This novel clustering combination strategy can leverage the information hidden in the original data representation and encoded in each cluster assignment to facilitate the generation of more stable clustering.

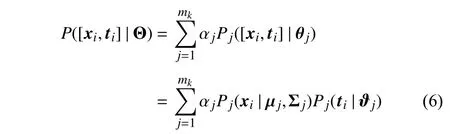
wheremkis the number of mixture components which also corresponds to the number of clusters in the final ensemble clustering. Each mixture component is parameterized byθjwhile αj>0 is regarded as the mixing coefficient correspondingtothepriorprobabilityofeachclusters.In addition,αj=1. Notethatrandomvariablesxiandtiare assumed to be conditionally independent to make the problem tractable. This assumption is reasonable sincetidescribes the inherent structure of the whole training set, which is relatively immune to a certain data pointxi.

In this paper, the instancexiis modeled as a random variable drawn from a marginal distribution described as a mixture of Gaussian distributions according to (6), i.e.,

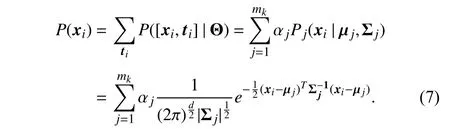
Here, each mixture component is parameterized by µjand Σj, where µjand Σjare thed-dimensional mean vector and the covariance matrix for each mixture component respectively.

Similarly, the cluster assignment vectortiis modeled as a random variable drawn from a marginal distribution described as a mixture of multinomial distributions according to (6), i.e.,

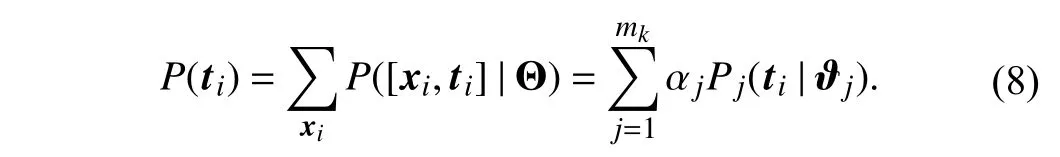
Here, each mixture component is parameterized by ϑj.Assume that the elements of the cluster assignment vectortiare conditionally independent, then

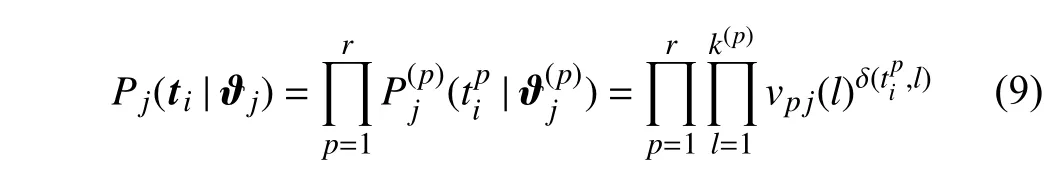
wherek(p)is the number of clusters in thepth base cluster. In addition, δ(,l) is the Kroneckerδfunction which returns 1 ifis equal toland 0 otherwise. The probability of the instance belonging to thelth cluster is defined asvpj(l) with

Based on the above assumptions, the problem of the clustering combination is now transformed into a maximum likelihood estimation problem. The optimal parameterΘ∗w.r.t.is found by maximizing the log-likelihood function as follows:

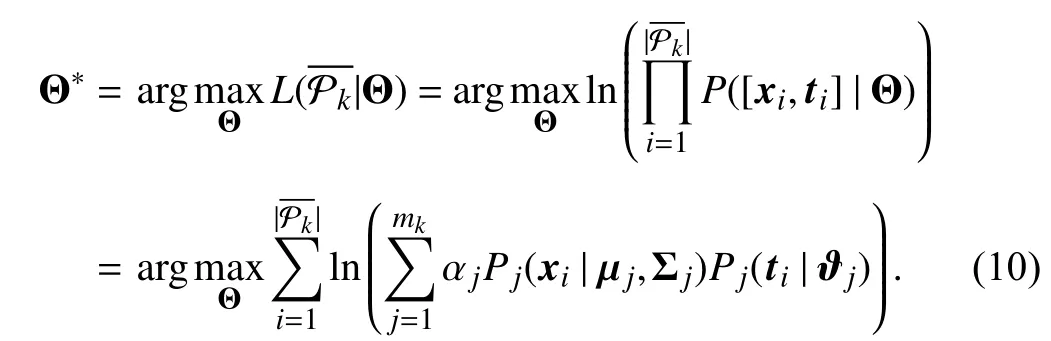
The optimal parameter Θ∗w.r.t.is found in the same way.However, as all the parametersΘ={αj,µj,Σj,ϑj|1 ≤j≤mk}are unknown, the problem in (10) cannot generally be solved in a closed form. Thus, the EM algorithm is used to optimize (10). In order to perform the EM algorithm, the hidden variablezi∈{1,2,...,mk} is introduced to represent the corresponding mixture component generating [xi,ti], i.e.,zi=jif [xi,ti] belongs to thejth mixture component.According to the Bayes’ theorem, theE-step of the EM algorithm can be obtained by estimating the posterior distribution of the hidden variablezias follows:

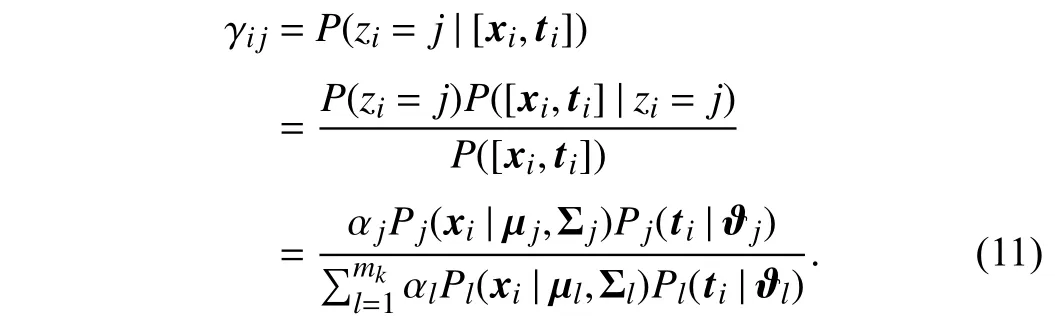
In other words, γijgives the posterior probability that [xi,ti]is drawn from thejth mixture component. Given the value of γijfrom theE-step, theM-step aims to maximize the loglikelihood functionL(). The mean vector µjand the covariance matrix Σjare derived as follows:

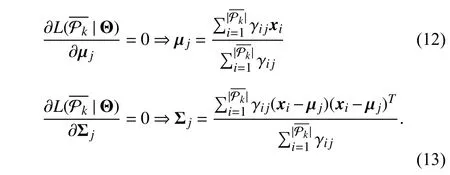
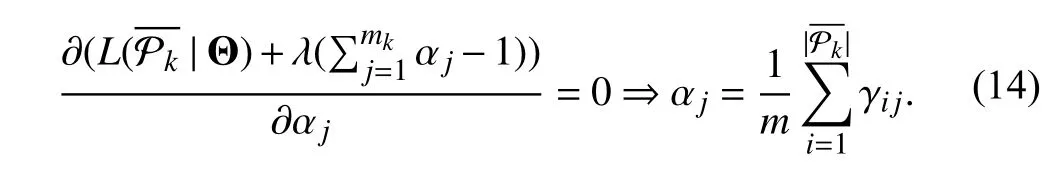
Similarly, the optimal value ofvpj(l) is obtained as follows:

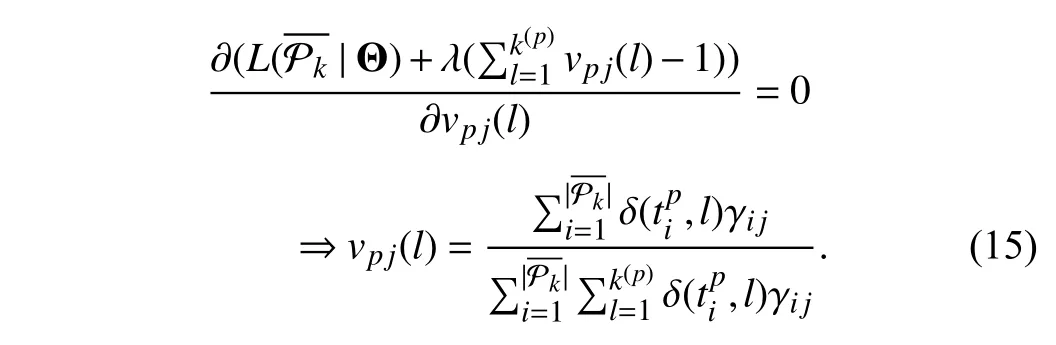
In summary, for each iteration, theE-step estimates the posterior distribution of the hidden variableziaccording to the current parameters while theM-step updates the optimal values of all parameters according to (12)−(15).

3)Label-Specific Features Construction:According to the inducedmixingdistribution on,Pkisdivided intomkdisjointclusters donated as {}. Thefinal clusterassignment of each instancein Pkcan be definedas follows:

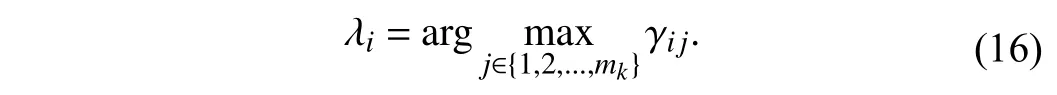
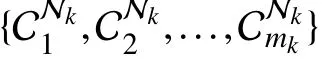
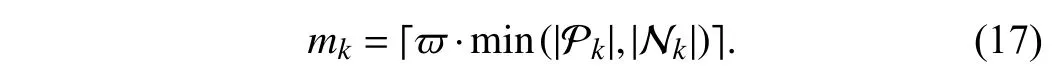
Here, ϖ ∈ [0, 1] is a ratio parameter controlling the number of clusters Pkand Nkretained, and |·| returns the set cardinality.

Conceptually, cluster centers characterize the inherent structure of the positive and negative instances. Thus,clustering centers can be used as prototypes to construct labelspecific features which are derived from more stable clustering. Similar to LIFT, the mapping ϕk:X →Zkcan be created according to (2).

4)Predictive Model Induction:Similar to LIFT, SENCE transforms the training set D into a new binary training setBkfor each class label according to (3). Any binary learner L can be applied to induce a classification modelgk:Zk→R forlkbased on Bk. After that, an associated label set is predicted for an unseen exampleu∈X according to (4).

Algorithm 1 summarizes the procedure of SENCE. SENCE firstly performs clustering several times to re-represent instances for each label (Steps 2−4); After that, the EM algorithm is used to yield more stable clustering (Steps 5−15)and label-specific features are constructed for each class label(Step 16); Then, a family ofqbinary classification models are induced based on the constructed label-specific features (Steps 18−21); Finally, an unseen instance is fed to the learned models for predicting the relevant labels (Step 22).

Algorithm 1 The Pseudo-Code of SENCE

IV. EXPERIMENTS

A. Experimental Setup

Given the multi-label data set S={(xi,Yi)|1 ≤i≤m}, |S|,dim(S) andL(S) denote the number of examples, number of features and number of possible class labels, respectively. In addition, several other multi-label properties [1], [15] are de noted as

•LCard(S)=(1/m)|Yi|:Label cardinality measures the average number of labels per example;

•LDen(S)=LCard(S)/L(S):Label density normalizesLCard(S)by the number of possible labels;

•DL(S)=|{Y|(x,Y)∈S}|:Distinct label sets counts the number of distinct label sets existing in S;

•PDL(S)=DL(S)/|S|:Proportion of distinct label sets normalizesDL(S) by the number of examples.

Table II summarizes the detailed characteristics of the benchmark multi-label data sets employed in the experiments.Data sets shown in Table II are roughly ordered by | S|. The 18 benchmark data sets exhibit diversified multi-label properties which provide a solid basis for thorough performance evaluation.

To validate the effectiveness of the proposed approach, six state-of-the-art multi-label learning approaches are used for comparative studies.

•LPLC [42]:A second-order multi-label learning approach which exploits the local positive and negative pairwise label correlations by maximizingk-nearest neighbor (kNN)-based posterior probability [k=10,α=0.1].

•LIFT [6]:A first-order multi-label learning approach,which induces classifiers with label-specific features generated via conducting clustering analysis for each class label[Base learner: Linear kernel support vector machine (SVM),r=0.1].

•LLSF [30]:A second-order multi-label learning approach based on label-specific features generated by retaining a different subset of original features for each class label[α=0.5,β=0.5,γ=0.5].

•MLSF [34]:A high-order multi-label learning approach based on label-specific features, which performs sparse regression to generate tailored features by retaining a different subset of original features for a group of class labels[ϵ=0.01,α=0.8,γ=0.01].

•LIFTACE [8]:A high-order multi-label learning approach based on label-specific features generated by considering label correlations via clustering ensemble techniques [Base learner:linear kernel SVM,r=0.1, γ =10].

•WRAP [38]:A high-order multi-label learning approach which performs label-specific feature generation and classification model induction in a joint manner [λ1=0.5, λ2=0.5,λ3=0.1, α =0.9].

For each comparing approach, parameter configurations suggested in respective literature are stated above. For SENCE shown in Algorithm 1, the parameter configuration corresponds to ϖ=0.4 andr=5. Moreover, LIBSVM [43] is employed as the binary learning algorithm L and thek-means algorithm is employed as the base clustering algorithm.

In addition, given the test set T ={(xi,Yi)|1 ≤i≤t} and a family ofqlearned functions {f1,f2,...,fq}, six evaluation metrics [1] widely-used in multi-label learning are utilized in this paper to evaluate the performance of each comparing approach:

•Hamming loss:

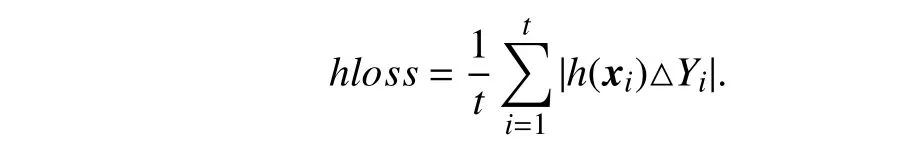
Hamming loss evaluates the fraction of instance-label pairs which are misclassified. Here,h(xi)={lk|fk(xi)>0,1 ≤k≤q} corresponds to the predicted set of relevant labels forxi,and △ stands for the symmetric difference between two sets.

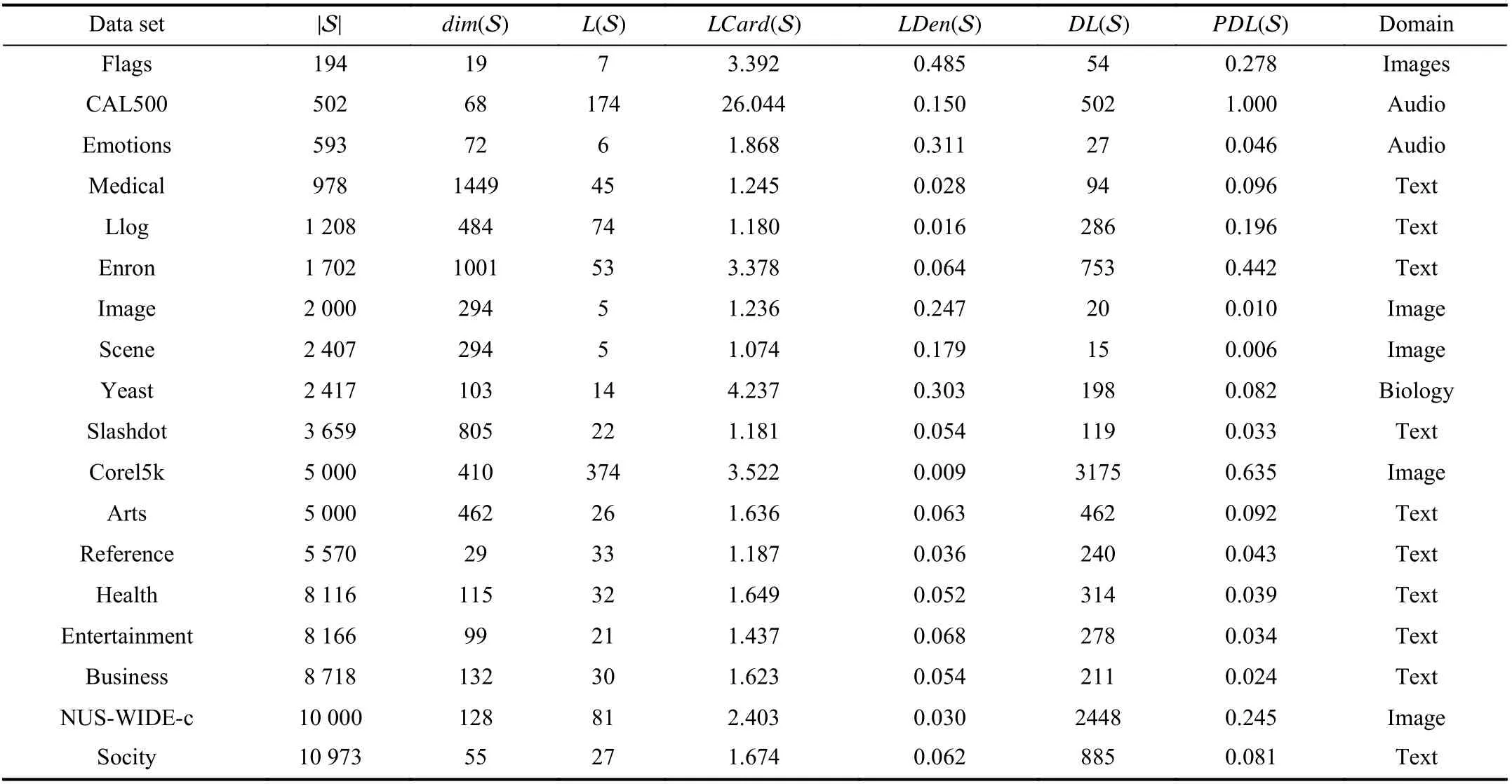
TABLE II CHARACTERISTICS OF THE EXPERIMENTAL DATA SETS

•Ranking loss:

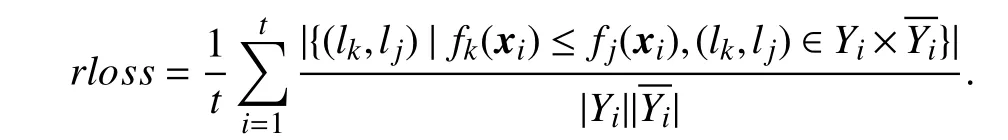
Ranking loss evaluates the fraction of relevant-irrelevant label pairs which are reversely ordered. Here,is the complementary set ofYi⊆у.

•One-error:

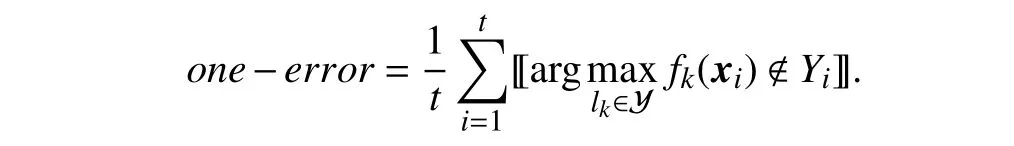
One-error evaluates the fraction of examples whose topranked predicted label is not in the ground-truth relevant label set. Here, 〚 π〛 returns 1 if predicateπholds and 0 otherwise.

•Coverage:

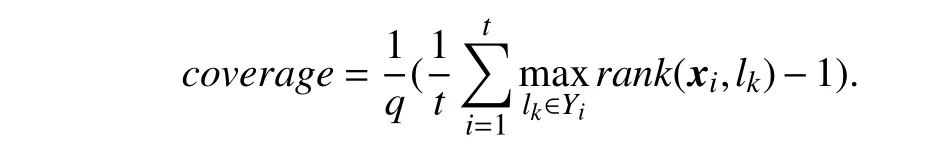
Coverage evaluates the average number of steps needed to move downtherankedlabel list inorderto coverallrelevant labels. Here,rank(xi,lk)=〚fj(xi)≥fk(xi)〛returnsthe rank oflkwhen all class labels in у are sorted in descending order according to {f1(xi),f2(xi),...,fq(xi)}.

•Average precision:

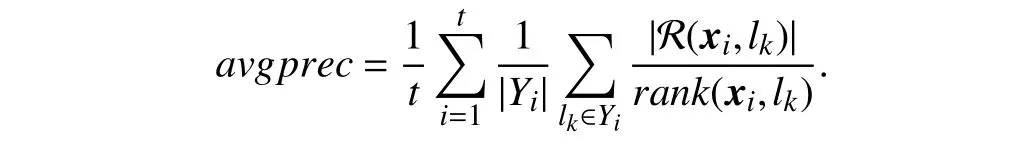
Average precision evaluates the average fraction of relevant labels which rank higher than a particular relevant label. Here,R(xi,lk)={lj|rank(xi,lj)≤rank(xi,lk),lj∈Yi}.

•Macro-averaging AUC:

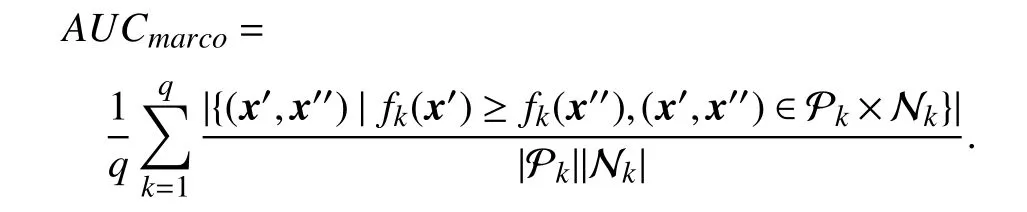
Macro-averaging AUC evaluates the average AUC value across all class labels.

B. Experimental Results

Ten-fold cross-validation is performed on each benchmark data set, where the mean metric value as well as standard deviation are recorded. Tables III and IV report detailed experimental results in terms of each evaluation metric where the best performance on each data set is shown in boldface.

In addition, the widely-accepted Friedman test [44] is employed here for statistical comparisons of multiple algorithms over a number of data sets. Table V summarizes the Friedman statisticsFFand the corresponding critical values on each evaluation metric at α=0.05 significance level. As shown in Table V, the null hypothesis of “equal”performance among comparing approaches should be clearly rejected in terms of each evaluation metric.

Therefore, the Bonferroni-Dunn test [45] is employed as the post-hoc test [44] to analyze the relative performance among comparing approaches where SENCE is treated as the control approach. Here, the difference between the average ranks of SENCE and one comparing approach is calibrated with the critical difference (CD). Their performance difference is deemed to be significant if the average ranks of SENCE and one comparing algorithm differ by at least one CD. In this paper, we have CD = 1.8996 at significance level α=0.05 ask=7 andN=18.

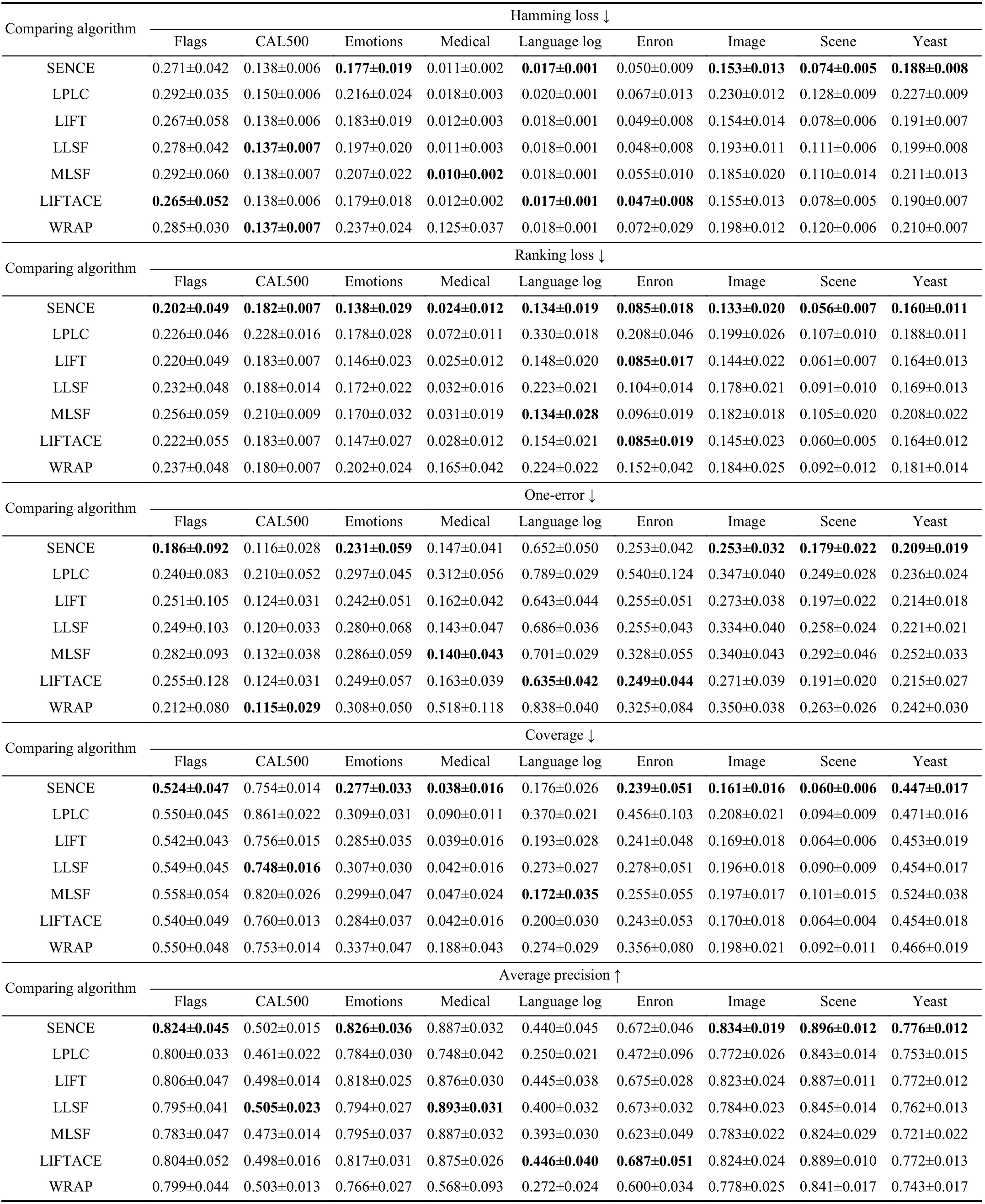
TABLE III EXPERIMENTAL RESULTS OF THE COMPARING APPROACHES ON THE FIRST NINE DATA SETS(↓: THE SMALLER THE BETTER; ↑: THE LARGER THE BETTER)

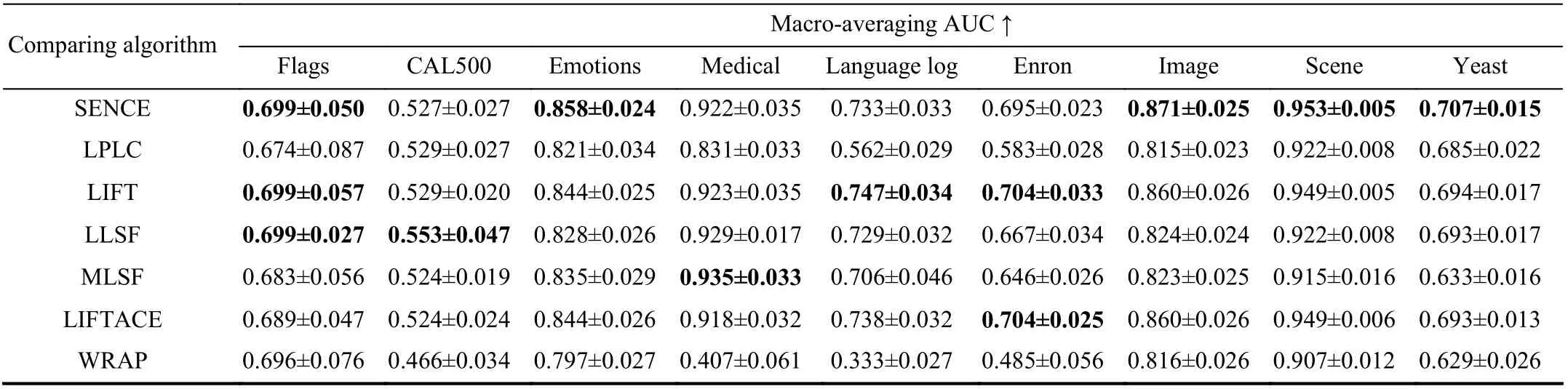
TABLE III EXPERIMENTAL RESULTS OF THE COMPARING APPROACHES ON THE FIRST NINE DATA SETS(↓: THE SMALLER THE BETTER; ↑: THE LARGER THE BETTER) (CONTINUED)

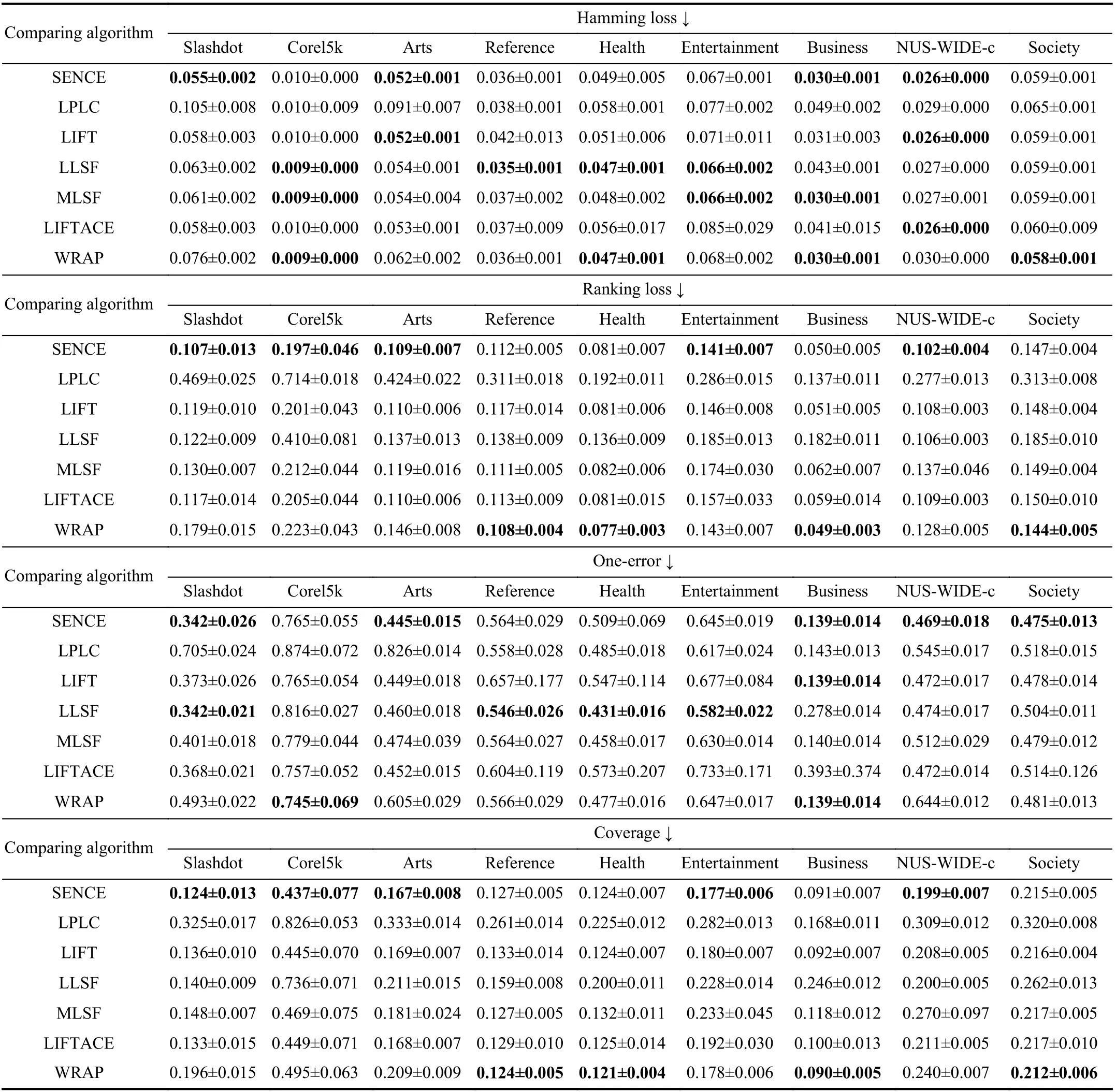
TABLE IV EXPERIMENTAL RESULTS OF THE COMPARING APPROACHES ON THE OTHER NINE DATA SETS(↓: THE SMALLER THE BETTER; ↑: THE LARGER THE BETTER)

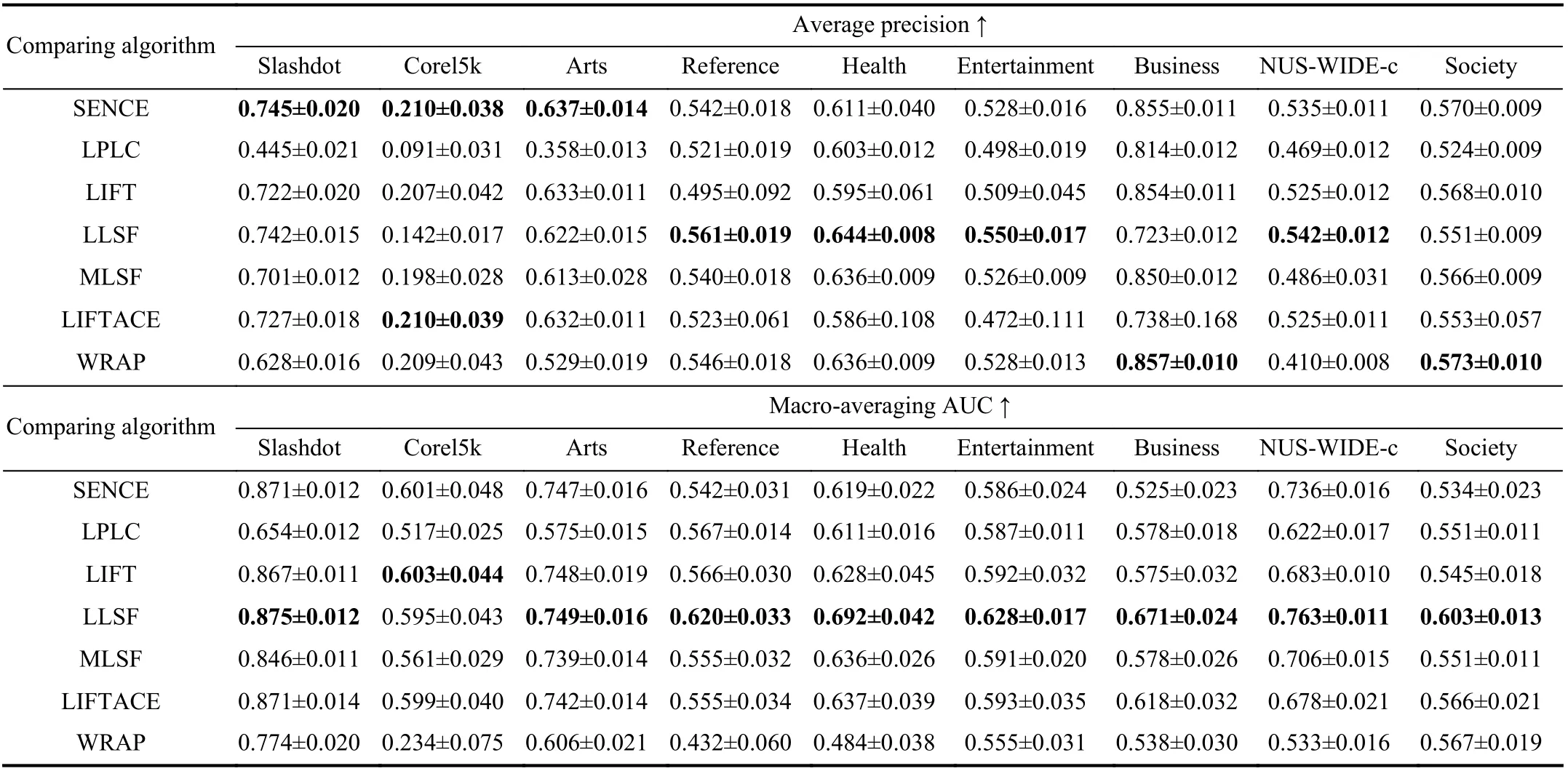
TABLE IV EXPERIMENTAL RESULTS OF THE COMPARING APPROACHES ON THE OTHER NINE DATA SETS(↓: THE SMALLER THE BETTER; ↑: THE LARGER THE BETTER) (CONTINUED)

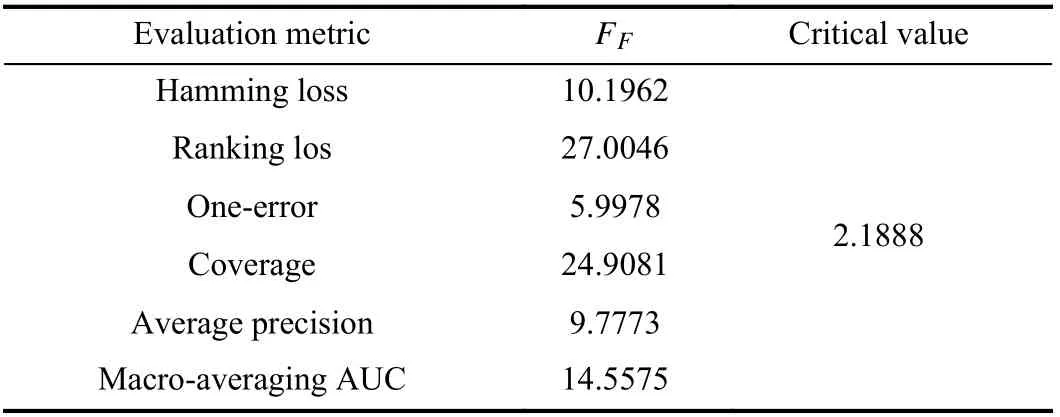
TABLE V FRIEDMANSTATISTICS FFINTERMSOF EACHEVALUATION METRIC AS WELLAS THE CRITICALVALUEAT 0 .05SIGNIFICANCE LEVEL(#COMPARINGAPPROACHESn=7, #DATASETS N=18)

Based on the reported experimental results, the following observations can be made:

• As shown in Fig. 1, it is impressive that SENCE achieves the lowest rank in terms of all evaluation metrics except macro-averaging AUC. Furthermore, all comparing approaches except LPLC and WRAP achieve statistically comparable performance in terms of macro-averaging AUC.

• Compared with approaches without label-specific features,SENCE significantly outperforms LPLC in terms of all evaluation metrics. These results clearly indicate the effectiveness of constructed label-specific features for multilabel label learning.

• Among approaches with label-specific features, SENCE significantly outperforms LLSF, MLSF and WRAP in terms of ranking loss and coverage. SENCE is comparable to LIFT in terms of all evaluation metrics. Furthermore, pairwisettests at 0.05 significance level show that SENCE achieves superior or at least comparable performance to LIFT in 97.2%cases out of 108 cases (18 data sets × 6 evaluation metrics).These results clearly indicate our proposed clustering ensemble-based strategy for label-specific features serves a more effective way in achieving stable clustering and strong generalization performance.

• SENCE is comparable to LIFTACE in terms of all evaluation metrics. Further pairwiset-tests at 0.05 significance level show that SENCE achieves superior or at least comparable performance to LIFTACE in 96.3% cases out of 108 cases (18 data sets × 6 evaluation metrics). These results clearly validate the effectiveness of the proposed clustering ensemble strategy employed in SENCE, as both SENCE and LIFTACE utilize clustering ensemble to facilitate the label-specific features construction.

All metric values are normalized in [0, 1], where for the first four metrics the smaller the metric value the better the performance and for the other two metrics the larger the metric value the better the performance.

C. Further Analysis

1)Parameter Sensitivity:As shown in Algorithm 1, there are two parameters for SENCE to be tuned, i.e. the number of base clustersrand the ratio parameterϖ. Fig. 2 illustrates how the performance of SENCE changes with varying parameter configurations ϖ ∈{0.1,0.2,...,1} andr∈{1,2,...,10} on three benchmark data sets (evaluation metrics: hamming loss and ranking loss). As shown in Fig. 2, the performance of SENCE is relatively stable as the value ofrincreases under the fixed value ofϖ. On the other hand, the performance of SENCE becomes stable as the value ofϖincreases beyond 0.4 under the fixed value ofr. Therefore, the value ofϖandris fixed to be 0.4 and 5 respectively for comparative studies in this paper.

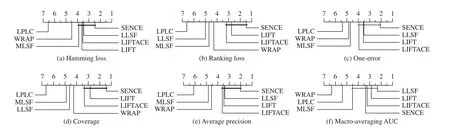
Fig. 1. Comparison of SENCE (control approach) against six comparing approaches with the Bonferroni-Dunn test. Approaches not connected with SENCE in the CD diagram are considered to have significantly different performance from the control approach (CD = 1.8996 at 0.05 significance level).

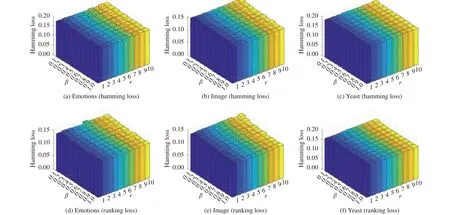
Fig. 2. Performance of SENCE changes with varying parameter configurations ϖ ∈{0.1,0.2,...,1} and r ∈{1,2,...,10} (Data sets: Emotions, image, yeast;First row: Hamming loss, the smaller the better; Second row: Ranking loss, the smaller the better).

2)Base Learner:Among the six comparing algorithms employed in Section IV-A, three of them are tailored towards concrete learning techniques. Specifically, LPLC is adapted from thek-nearest neighbor while LLSF and WRAP are adapted from linear regression. On the other hand, LIFT,LIFTACE and MLSF work in similar way as SENCE by transforming the multi-label learning problem so that any base learner can be applied thereafter. Considering that SENCE,LIFT, LIFTACE and MLSF rely on the choice of base leaner Lto instantiate learning approaches, Table VI reports their performance on 8 data sets instantiated with different choices of base learner L ( L ∈ {SVM,k-nearest neighbor (kNN),classification and regression tree (CART)}). As shown in Table VI, the following observations can be made: a) The choice of base learner has a significant influence on the performance of each algorithm; b) SENCE achieves superior or comparable performance compared to other algorithms in most cases with different base learners; c) SENCE tends to perform better when SVM is used as the base learner other thankNN and CART.

3)Ablation Study:In training phase, SENCE employs multiple base clusters and a mixture model to yield the final clustering. To analyze the rationality of these components,ablation study on two variants of SENCE is further conducted in this subsection. Specifically, SENCEKemploysk-means to obtain clusteringresultsonaugmented instancesinsteadof a mixture model;SENCEGemploys onemixtureGaussian model to yield clustering results on original instance representations without feature augmentation.

Table VIIreportsdetailed experimental results ofSENCE and its two variants SENCEK, SENCEGon8benchmarkdata sets. Compared with SENCEG,SENCE achieves statistically superior or comparable performance in all cases. These results clearly validate the usefulness of multiple base clusters which augment the original instance representations with cluster assignments. Compared with SENCEK, SENCE achieves statistically superior or comparable performance in all cases.These results clearly indicate that the mixture model might be more effective for integrating preliminary clustering results.

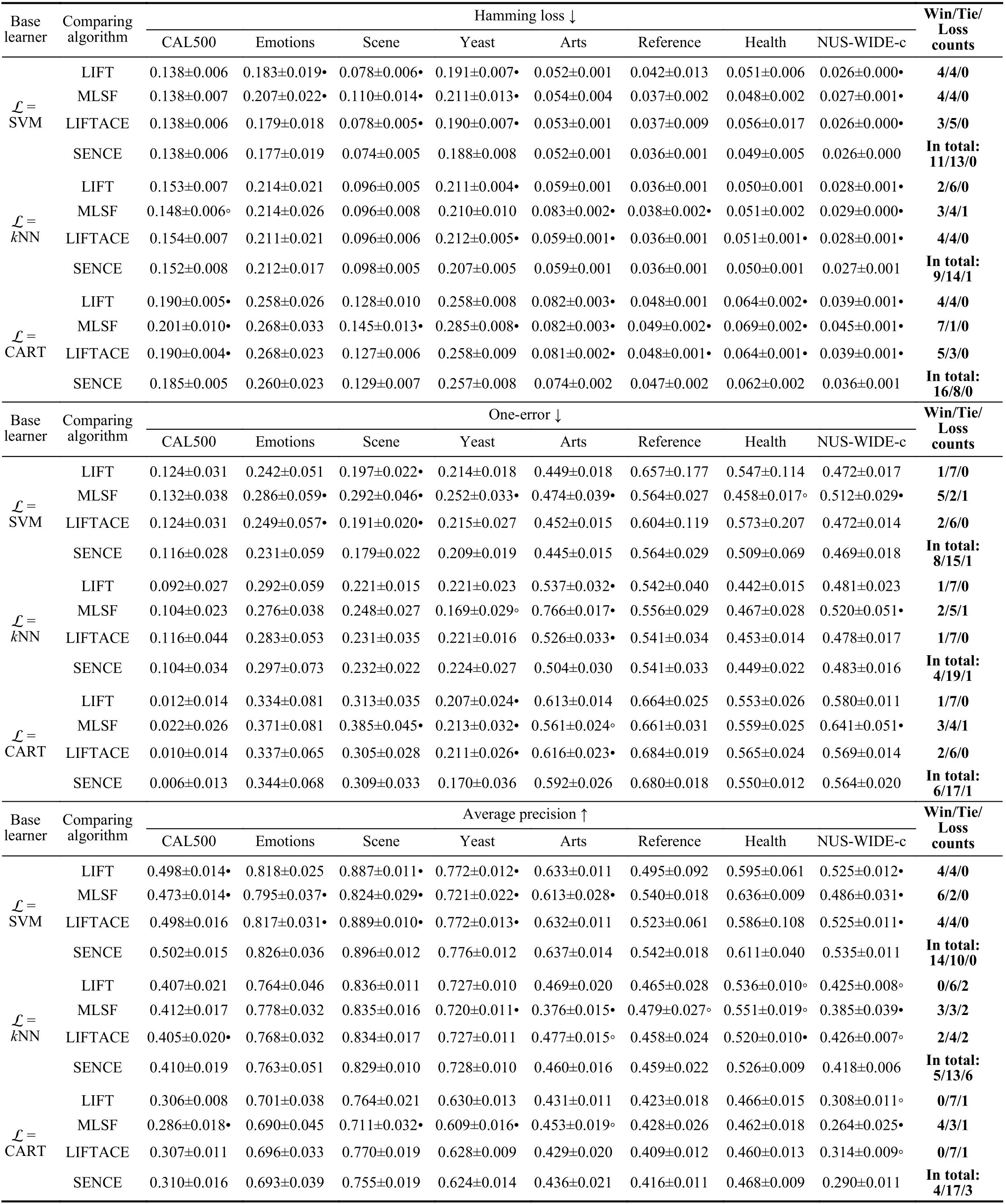
TABLE VI EXPERIMENTALRESULTS OF THE COMPARINGAPPROACHES INSTANTIATED WITHDIFFERENTBASE LEARNERSL ( L ∈{SVM, K-NEAREST NEIGHBOR (KNN), CLASSIFICATION AND REGRESSION TREE (CART)}). IN ADDITION, •/◦ INDICATESWHETHER THE PERFORMANCE OF SENCE ISSTATISTICALLY SUPERIOR/INFERIOR TOTHE COMPARING APPROACHES ON EACH DATASET (PAIRWISET-TEST AT0.05 SIGNIFICATE LEVEL)

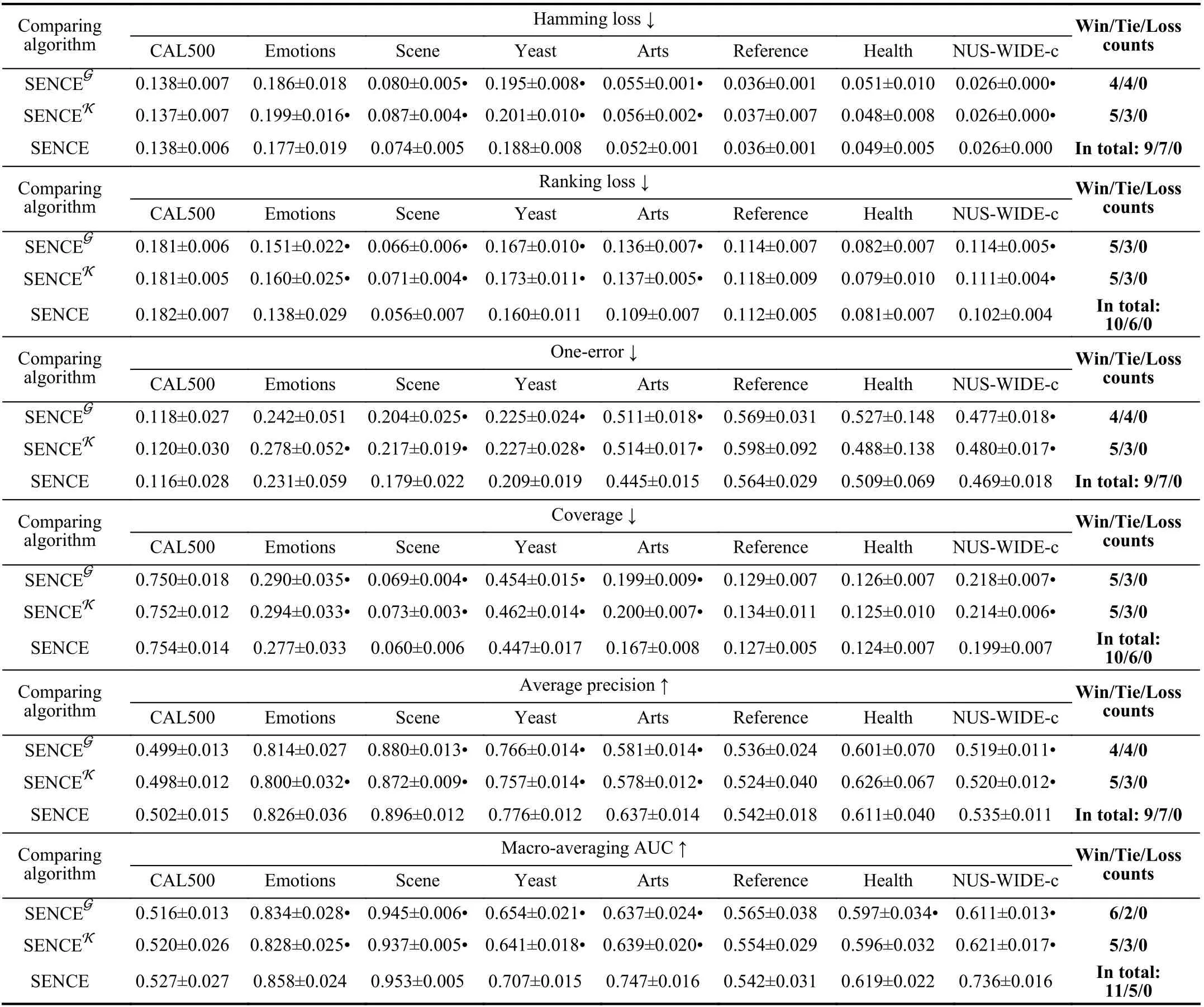
TABLE VII EXPERIMENTAL RESULTS OF SENCE AND ITS TWO ABLATED VARIANTS ON EIGHT DATA SETS. IN ADDITION, •/◦ INDICATES WHETHER THE PERFORMANCE OF SENCE IS STATISTICALLY SUPERIOR/INFERIOR TO THE VARIANTS ON EACH DATA SET (PAIRWISE T-TEST AT 0.05 SIGNIFICATE LEVEL)

4)Algorithmic Complexity:Let FL(m,b) be the training complexity of the binary learner L w.r.t.mtraining examples andb-dimensionalfeature(s.Thetraining complexity of SENCEcorre)s) ponds toOq(I(md2+r「ϖ·m⏋2+「ϖ·m⏋d3)+FL(m,「ϖ·m⏋),whered3isderived from the covariance matrix inversion andIis the number of iterations. The testing co( m(plexityofSE NCE ove)r)u nseen instanceucorresponds to Oqd「ϖ·m⏋+(「ϖ·m⏋),whereFL(b)′is thetesting complexity of L in predicting one unseen instance withbdimensional features.

Fig. 3 illustrates the execution time (training phase as well as testing phase) of all the comparing algorithms investigated in Section IV-A on five benchmark data sets emotions, enron,image, corel5k, and NUS-WIDE-c. Across the 5 data sets,their number of examples, features and class labels range from 593 to 10 000, 72 to 1001, and 5 to 374, respectively. The training time of SENCE is relatively comparable to the comparing approaches except LPLC and LLSF. Furthermore,the test time of SENCE is higher than LLSF and WRAP while relatively comparable to the other comparing approaches.Note that due to the cubic computational complexity of SENCE w.r.t.d(i.e., the number of features in input space),the proposed approach may have problems when applied to data sets with high-dimensionality features. We will leave this for future works.

V. CONCLUSIONS

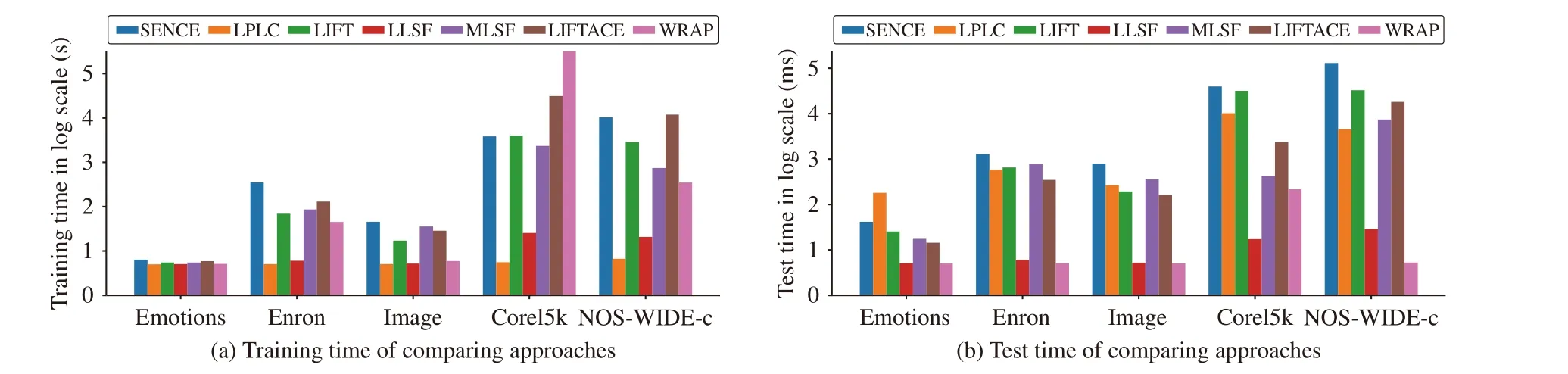
Fig. 3. Running time (training/test) of each comparing approach on five benchmark data sets. For histogram illustration, the y-axis corresponds to the logarithm of running time.

In this paper, the problem of generating label-specific features for multi-label learning is investigated. A novel approach for label-specific features generation is proposed,which stabilizes the generation process of the label-specific features via clustering ensemble techniques. Specifically, the final clustering used to construct label-specific features is obtained by fitting a mixture model on instances augmented with base cluster assignments via the EM algorithm.Comprehensive experimental studies validate the effectiveness of the proposed approach against state-of-the-art multilabel learning algorithms. In the future, it is interesting to consider generating label-specific features by exploiting label correlations based on the proposed SENCE and investigate a more general joint distribution by taking dependency of the original instance and corresponding cluster assignment vector into account.

ACKNOWLEDGMENTS

We thank the Big Data Center of Southeast University for providing the facility support on the numerical calculations in this paper.