基于GEO-GRU的电梯滑移量预测方法*

李 科 陈向俊 任玉荣 王剑平 傅正杨

1浙江省特种设备科学研究院 杭州 310053 2浙江省特种设备检验技术研究重点实验室 杭州 310053 3金华市食品药品检验检测研究院 杭州 310053

0 引言

在高度城市化的今天，城市中的高层建筑数量越来越多，电梯正逐步向高处发展，对电梯钢丝绳也提出了更高的要求，电梯钢丝绳的韧性、抗拉强度、刚性都是影响钢丝绳使用寿命的因素[1]。电梯在上升的过程中，经常会因为钢丝绳与轮槽之间摩擦力不够而产生钢丝绳打滑的现象[2]，容易引发安全事故。除打滑外，钢丝绳还有滑移的固有特性，与打滑不同，其本质是钢丝绳两端张力不均匀，又因为钢丝有弹性，在张力差作用下会有不同程度的伸长，其大小取决于很多因素[3]。由于钢丝绳滑移量很小，通常只有数毫米，在瞬时很难对其进行测量，但通过长时间的运行和实验，形变差在累计后形成的滑移量是可以观测的。值得注意的是，钢丝绳的滑移对电梯的曳引能力有一定影响，并且是不可避免的[4]，故对电梯滑移量的测试和分析是非常必要的。

查询相关文献，王常辉[5]对电梯做了125%载荷试验，分析了电梯滑移量的具体范围，但未考虑电梯的服役时长对滑移的影响；伍磊等[6]分析了电梯曳引轮磨损案例的成因，指出了滑移和钢丝绳磨损之间的关系，但未具体对滑移量进行度量。沈永强等[7]对电梯紧急制动时的滑移做了实验分析，从曳引力的大小反推滑移量，较好地解释了滑移的成因，但是实验存在局限，不能很好体现滑移量随时间的变化规律。由于目前对电梯滑移量的研究多是以125%额定载荷实验为基础，对电梯滑移量随服役时长的变化研究较少，部分研究存在局限和不足。为解决这一问题，本文从形成滑移量的理论公式入手，考虑影响滑移量大小的主要因素，计算出归一化后的滑移量，并采用基于金鹰优化算法优化的门控循环单元神经网络（GEO-GRU）模型挖掘历史滑移量中的数值特征关系，并对电梯后续滑移量进行准确预测。GRU模型为循环神经网络(RNN)的一种改进版本[8]，可以有效挖掘时间序列的非线性特征，在故障诊断、天气预测等方面都有着广泛应用，适合于对滑移量这种混沌数据进行学习预测。然而，GRU模型本身存在问题，本文利用金鹰优化算法（GEO）对模型进行优化，进一步提高模型的泛用性和可靠性。基于实际测量的有效数据，利用GEO-GRU模型对滑移量进行预测，最后得到电梯滑移量随服役时长的变化规律，预测后续使用时滑移量的大小，这可为电梯的滑移测量提供参考，提高电梯安全系数。

1 滑移量理论分析

1.1 滑移的种类

电梯制动滑移主要包括在制动轮与闸瓦片之间形成的滑动位移和钢丝绳在曳引轮上形成的滑动2大类，在实际工作中，2种滑动有可能分别存在也有可能一起存在。钢丝绳滑移会导致电梯意外移动和坠落，图1为电梯钢丝绳的工作原理。

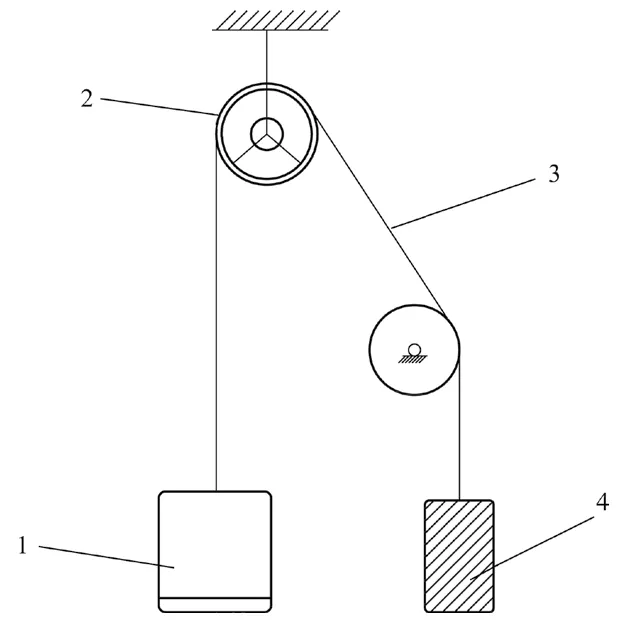
图1 电梯工作原理

钢丝绳两侧的张力一般是不相等的，根据图1可以推断，电梯两侧的钢丝绳张力可表示为

式中：T1和T2为线绳中的张力，α为线绳缠绕轮子的角度，f为等效摩擦系数。

制动轮滑移是制动轮在制动过程产生的，一般的抱闸式制动器会预留一定的抱闸距离，电梯制动时闸瓦片和制动轮开始靠拢，这个过程中两者之间的摩擦力逐渐增大，抱闸距离逐渐减小，最后曳引轮不断减速到停止转动。由GB7588—2003《国家电梯制造与安装安全规范标准》可知，缓冲器减速度平均值最大不能超过9.8 m/s2，又因为制动器的减速度比缓冲器更小，故滑移是不可避免的。

一般情况下，曳引轮与钢丝绳之间的摩擦力为静摩擦力。电梯在楼层中能顺利升降和停放依靠钢丝绳与曳引轮之间足够的摩擦力来保证，若电梯正常升降时突然进行制动，则电梯轿厢会在瞬间内急停，此时若电梯轿厢与对重的惯性力差值过大，惯性力将克服曳引轮与钢丝绳之间的静摩擦，同时静摩擦力被转化为动摩擦力，摩擦力已经不足以维持轿厢静止，钢丝绳发生滑移，电梯将失去平衡而开始移动。

1.2 滑移量计算模型

当曳引轮顺时针旋转（轿厢上升）和逆时针旋转（对重上升）时，钢丝绳的滑动位移是不同的，假设轿厢内无载荷，本文从顺时针和逆时针旋转分别分析曳引轮的滑动位移。图2所示为曳引轮旋转时的滑动模型。

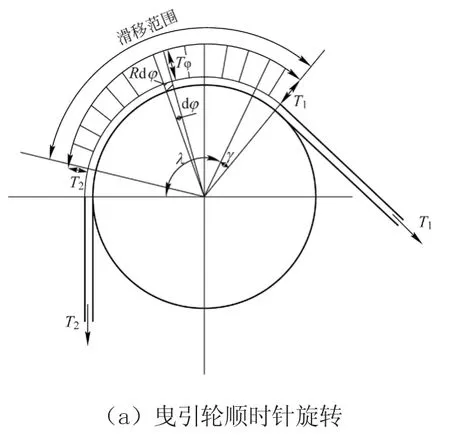
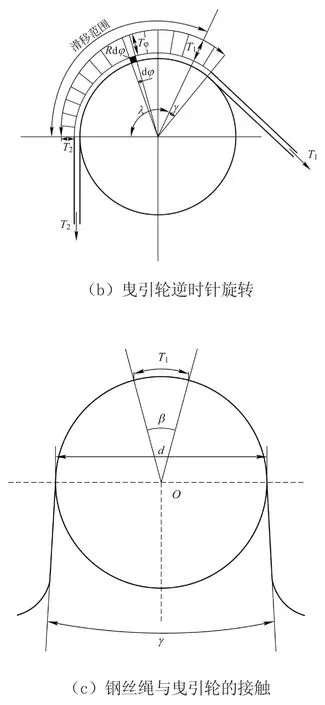
图2 曳引轮旋转时的滑动模型

图2c中，假设钢丝绳滑动位移有一段无穷小长度区域，钢丝绳在张力Tφ作用下伸长量为R·dφ,卸载状态下的单元长度为dl，c为单位载荷下每单位长度的钢丝伸长量。

可得到钢丝绳和曳引轮之间的等效摩擦系数f

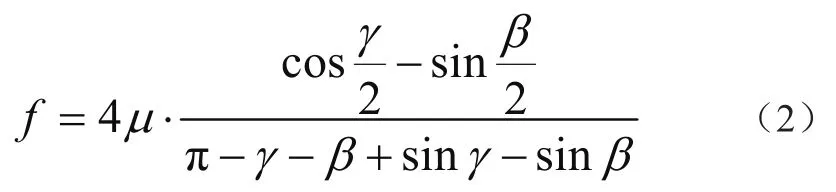
当曳引轮顺时针旋转时，通过计算，可以得到钢丝绳从C点到A点的滑动距离s1为

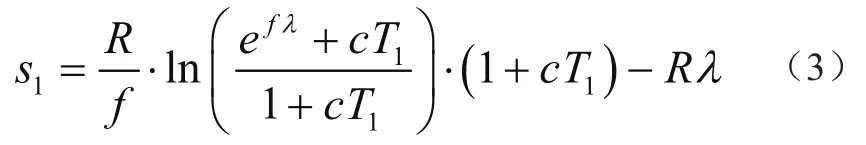
当曳引轮逆时针时针旋转时，同样可以计算出钢丝绳从C点到A点的滑动距离s2为

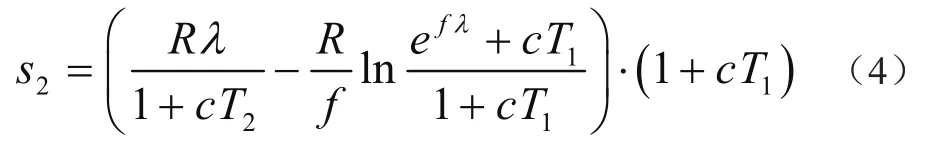
根据式（3）、式（4）可得到曳引轮顺时针和逆时针旋转时钢丝绳的相对滑移，然后在确定钢丝绳的型号后，可以计算相对于曳引轮钢丝绳的滑动位移的阈值，并判断牵引力大小是否满足要求。随着电梯服役时间的增加，电梯各方面性能会随之下降，钢丝绳的滑动位移逐渐增大，滑移量的变化是明显反映电梯性能的特征参数。

影响滑移量的因素有很多，除人为安装因素之外，钢丝绳的型号、曳引轮两侧钢丝绳的载荷差以及高度等都会对钢丝绳的滑移造成一定影响。不同型号的钢丝绳有不同的弹性模量，弹性模量越大，钢丝绳越不易变形，滑移量也就越小；曳引轮两侧的张力差越大，弹性伸长的变化就越大，形成的滑移量也越大，电梯的曳引比和高度同样对滑移量有影响，但其影响较小且易控制。综合多方面考虑，为了避免各因素对阈值的影响，将滑动位移转换为每单位长度的值进行分析和计算。假设电梯的曳引比为1：1，钢丝绳型号为8×19S+NF，轿厢载荷为空载，结合公式（3）、式（4）将滑动位移归一化，归一化后的滑动位移的阈值可写为

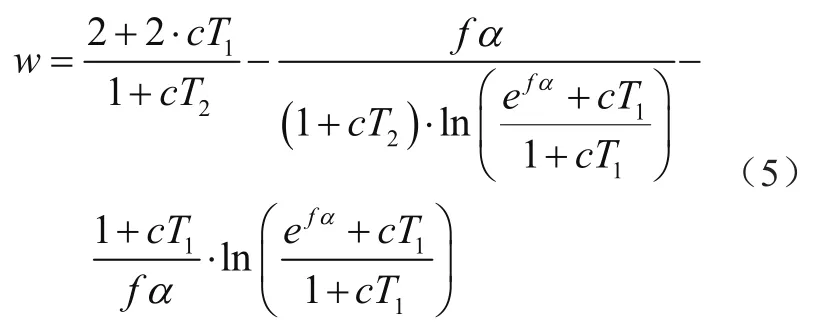
对于任何电梯，可以通过将电梯的相关参数代入式（5）来获得归一化的滑动位移。

2 算法理论

2.1 GRU神经网络模型

GRU是循环神经网络的一种，其在传统长短期神经网络LSTM上进行改进，在继承了LSTM的长短期记忆能力和梯度问题解决能力的基础上，通过优化神经元内门限个数，提升了模型性能，使GRU有着更好的拟合能力，同时减少模型参数，降低过拟合风险[10]。

GRU神经元的结构如图3所示，其通过2个Sigmoid构成的更新门与重置门，来对时序数据信息进行筛选，利用Sigmoid函数将前记忆状态信息与当前输入的数据进行函数变换，实现数据信息的记忆与丢失[11]。与传统的LSTM相比，GUR的最大改进是将LSTM中的遗忘门和输出门整合为一个更新门限Zt，并将隐藏状态和网络记忆合并为一个输出隐藏状态。以此使得GRU模型拥有更少的参数，且不容易发生过拟合；同时由于参数减少，使得计算量大大降低，极大提升了模型的效率和实用性。

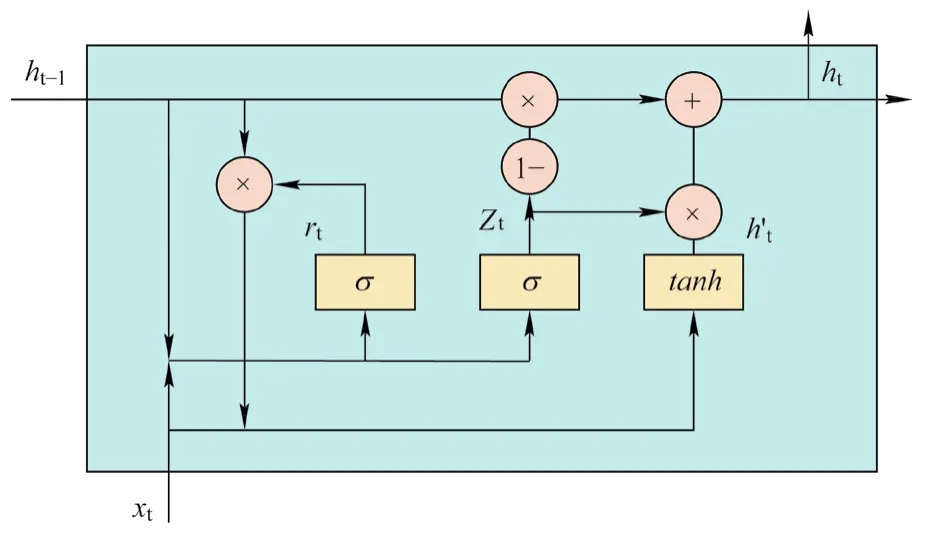
图3 GRU神经元结构

t时刻的GRU 神经元状态的中间变量计算公式为

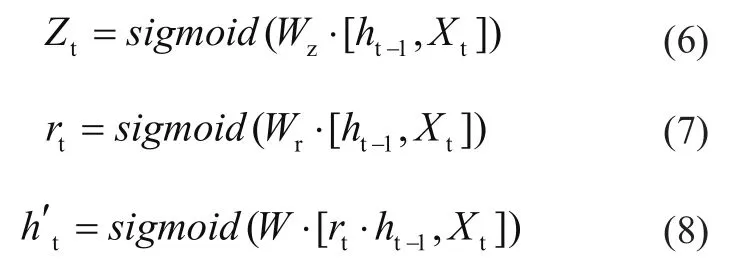
其中，Zt为更新门控，Zt越接近1，表示所记忆的数据信息越多；rt为重置门控，与更新门共同组成GRU的门系统； h＇t为包含当前输入信息的中间变量。ht-1为上一时刻的隐藏状态输出，Xt为当前状态输入，W为可训练的权值矩阵。神经元输出为

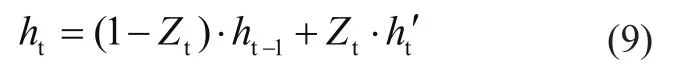
GRU模型中重置门控制保存上一神经元输出数据特征的权值，更新门控制当前神经元输入数据信息的权值，中间权值通过训练集训练更新，并在训练完成后保存，形成预测模型。

2.2 金鹰优化算法

金鹰优化算法（Golden Eagle Optimizer，GEO）是一种从金鹰捕食行为上获得灵感的元启发式算法[12]，相较于其他方法，具有收敛速度快，寻优能力强的特点。本文利用金鹰优化器对GRU算法的超参数进行优化，使其可以在滑移量的预测上获得更好的效果。

GEO灵感来自于金鹰的智慧，金鹰在捕食时会在不同阶段调整速度，在初期更多的进行巡游于寻找，在后期则倾向于攻击，这使得金鹰可以在有限的时间内捕获更好的猎物。

1）攻击行为（开发阶段）

攻击行为可以通过一个矢量来模拟，从金鹰当前的位置开始，到金鹰记忆中猎物的位置结束。金鹰的攻击矢量为

2）巡航行为（勘探阶段）

巡航向量根据攻击向量计算，巡航向量是圆的切向量，为了计算巡航矢量，需要首先计算切线超平面的方程。超平面的维数方程可以由超平面的任意点和与超平面垂直的向量确定，该向量称为超平面的法向量。超平面方程在三维空间中的标量形式为

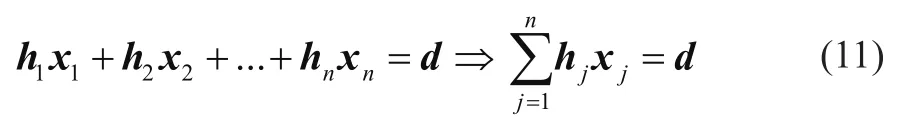
式中：H=[h1，h2，…，hn]为法向量，X=[x1，x2，…，xn]为变量向量。之后查找固定变量的值

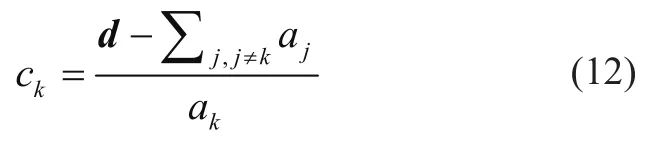
式中：ck为目标点的第k个元素，aj为攻击向量的第j个元素，ak为攻击向量的第k个元素。依此可以找到飞行超平面上的随机目标点。目标点的一般表示为

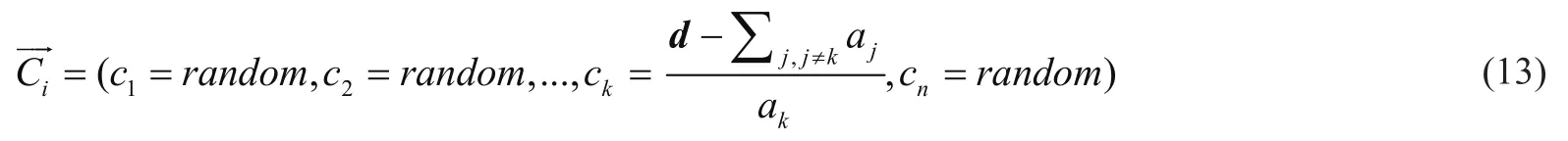
式中random∈[0,1]，随机数更新使得金鹰可以向随机目标点探索。

3）向新位置移动

金鹰的位移由攻击向量和目标位置组成，迭代步长为

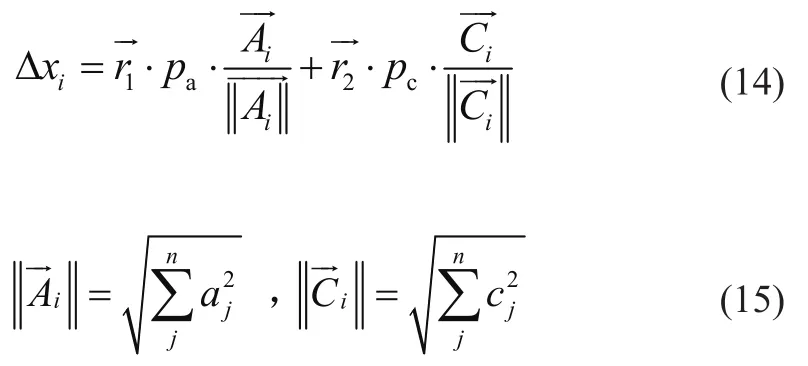
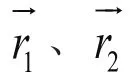
基于此可以求出金鹰的下一位置xt+1为

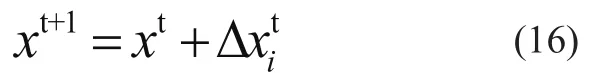
攻击系数pa和巡航系数pc的该更新公式为

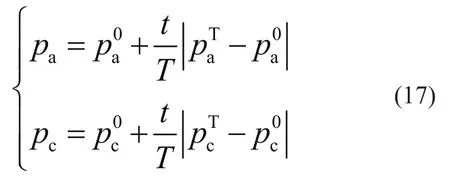
金鹰在巡航时会记住所经过的最佳捕猎位置，当金鹰的新位置适应性低于记忆位置时，金鹰为丢弃新位置重新寻找目标。从上文可知，金鹰会在前期更专注于全局探索，后期专注于更高的攻击倾向，这使得金鹰算法更不容易陷入局部最优解。

2.3 基于GEO-GRU模型的电梯滑移量预测方法

本文利用GEO算法对GRU算法进行优化，构成GEO-GRU预测模型对电梯滑移量进行预测。模型的预测流程如图4所示，将采集的电梯滑移量数据进行归一化之后划分为训练集测试集，将训练集的均方根误差RMSE作为GEO的适应度，对GRU模型的超参数进行寻优，并对滑移量进行预测，计算预测结果的均方根误差RMSE与平均绝对百分比误差MAPE对模型预测效果进行评判。其具体实现为

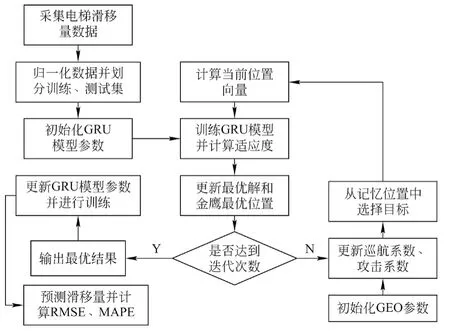
图4 GEO-GRU建模流程图

1）采集电梯滑移量数据，对其进行归一化为样本数据，并划分为训练集和测试集。

2）初始化GRU模型的超参数，包括时间窗步长、神经元个数、学习率、训练次数。

3）使用GEO算法对模型参数进行优化，使用RMSE作为模型适应度。

4）初始化金鹰的数量；计算适应度函数初始化群体记忆；初始化攻击系数、巡航系数；更新攻击系数、巡航系数；从种群的记忆计算攻击向量中随机选择猎物；计算巡航向量、计算步长向量、更新位置评估新位置的适应度函数；更新最优解及最优位置；判断金鹰算法是否满足最大迭代次数，若满足则输出当前最优金鹰位置及全局最优解，否则返回步骤4）重新迭代计算。

5）利用最优的参数构建GRU网络模型，并进行训练。

6）模型进行预测和有效性评价。

3 实例分析

3.1 数据采集

本文针对同型号电梯通过相同工况总共采集85组滑移量数据，经式（5）归一化后，将其前76组数据作为训练集，后9组数据作为测试集，以验证本文模型的可靠性。实验电梯的曳引比为1:1，轿厢载荷为空载，电梯轿厢质量1 300 kg，曳引轮直径640 mm，平衡系数0.48，钢丝绳型号为8×19S+NF，实验速度为1 m/s，归一化后数据如图5所示。

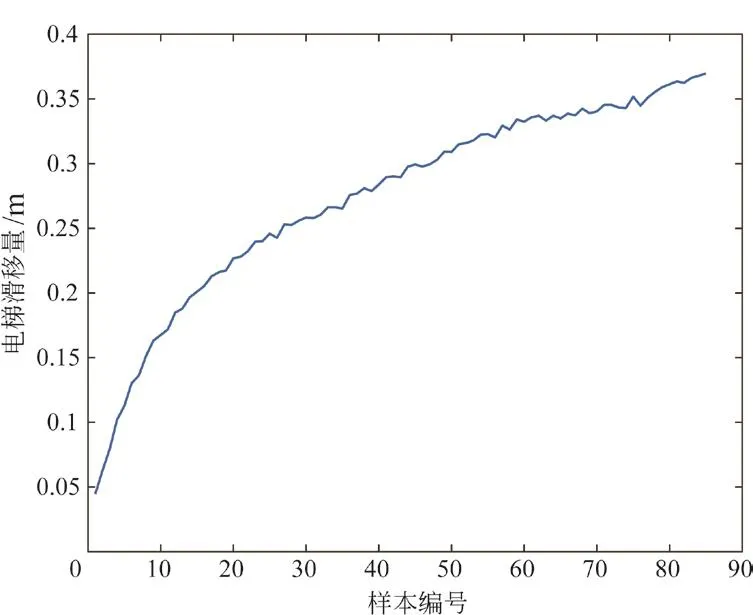
图5 归一化后电梯滑移量数据

3.2 评估指标

本文采用均方根误差RMSE（Root Mean Square Error）及平均绝对百分比误差MAPE（Mean Absolute Percentage Error）作为模型评判标准。RMSE越接近于0、MAPE越接近0时，可认为模型的预测精度愈高、模型性能愈好。RMSE与MAPE的计算公式为

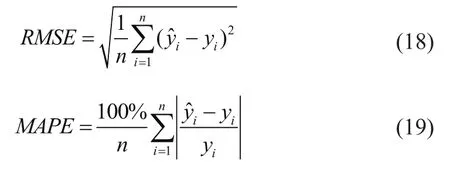
3.3 GEO-GRU模型预测

本文以GRU模型的均方根误差为适应度函数，利用GEO金鹰算法对GRU模型超参数进行优化，设定GRU模型迭代次数为100～2 000整数，神经元个数小于500，学习率取值[0.001，0.01]，优化后模型预测结果如图6所示，计算得优化参数后的模型预测结果均方根误差RMSE为0.001 3，平均绝对百分比误差MAPE为0.097%。

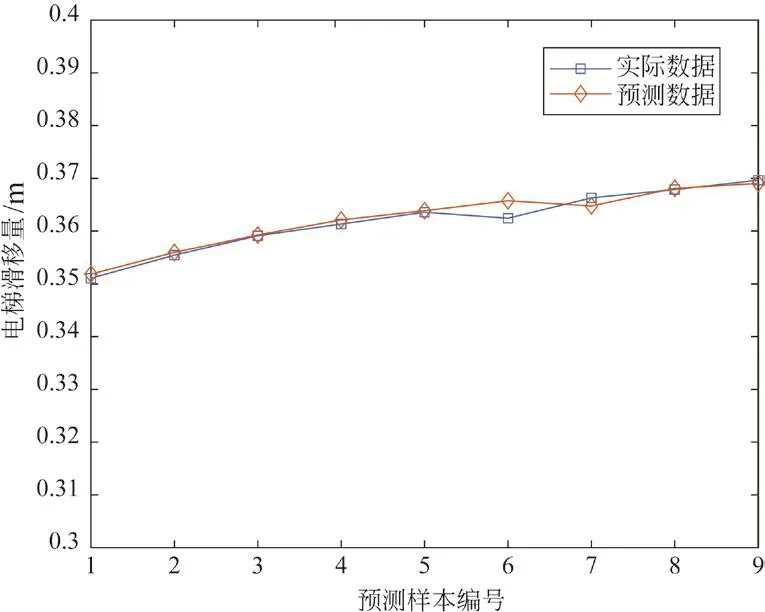
图6 GEO-GRU模型对滑移量预测结果

3.4 分析验证

为验证本文模型效果，利用传统LSTM模型和ESN模型对相同数据进行学习预测，并计算RMSE及MAPE，通过对比判断3种模型的预测效果。

设定LSTM模型的神经元个数为400，学习率为0.005，并在200步后降低为0.001，总训练步数为1 200；ESN模型设定储备池规模为400，使用前20组数据激活储备池，更新速度为1，预测结果如图7、图8所示。

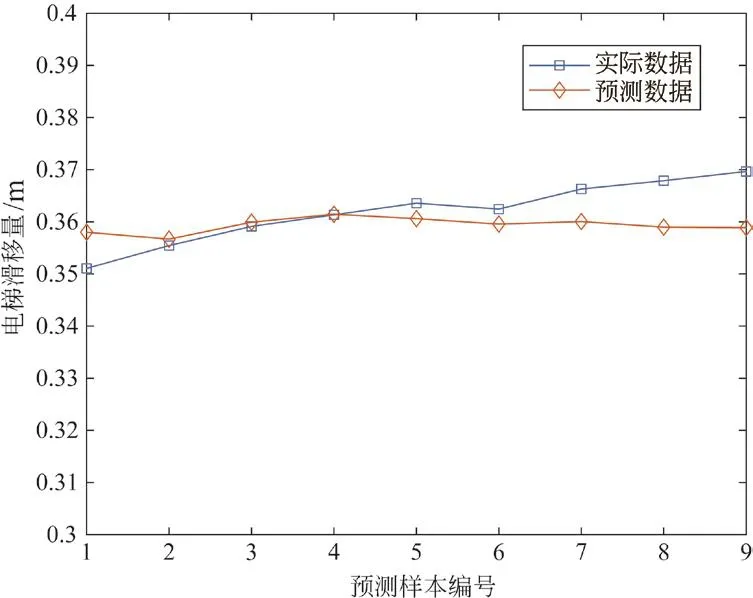
图7 LSTM模型预测结果

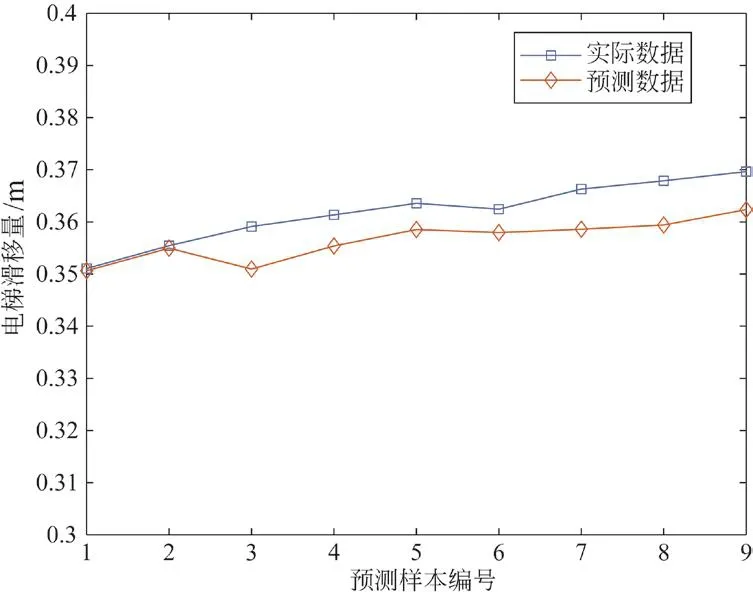
图8 ESN模型预测结果

计算各模型的均方根误差RMSE、平均绝对百分比误差MAPE，结果如表1所示。

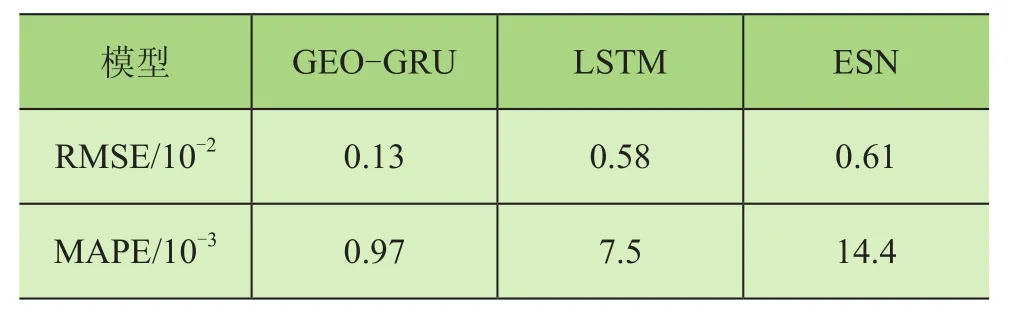
表1 滑移量预测性能对比

可以看出，本文所提出的GEO-GRU模型有着更好的预测精度。从图7中可知LSTM存在过拟合倾向和预测效果不佳。从图8可知ESN在处理较小数据量的时，由于需要出示数据进行储备池激活，性能略显不足，同时激活数值数量和训练数值数量的分配困难，难以获得较好的预测效果。由此可以说明，在电梯滑移量的预测上，GEO-GRU模型相较于其他传统模型有着更优秀的预测精度和稳定性。

4 结语

针对曳引式电梯的钢丝绳滑移量过大造成的电梯运行安全问题，本文在门控神经网络GRU的基础上，利用金鹰算法GEO对该模型超参数进行优化，提出了基于GEO-GRU的电梯滑移量预测方法，使得该GRU模型能够针对不同情况类型的电梯钢丝绳滑移变化进行很好的预测。本文通过采集同型号同工况下多台电梯的滑移量数据，并进行归一化处理，之后利用GEO-GRU模型对滑移进行预测，并与传统时序预测模型LSTM与ESN进行对比，发现本文所提出的GEO-GRU模型有着更优秀的预测能力和稳定性，相较于传统模型至少具有76%的性能提升，表明本文所提出的模型在电梯滑移量预测上具有更大的优势。