天然气管道肋条减阻数值分析

徐冰，李小玲，吴玉国

天然气管道肋条减阻数值分析

徐冰，李小玲，吴玉国

（辽宁石油化工大学 石油天然气工程学院，辽宁 抚顺 113001）

随着清洁能源的广泛应用，提高输气管道的输送效率成为热点问题，其中降低管输过程中的摩擦阻力至关重要。为探究三角形肋条在输气管道减阻中的应用效果，利用ANSYS⁃FLUENT软件对光滑管道和肋条管道中的湍流流动进行了数值模拟。结果表明，在近壁区域，肋条管道与光滑管道的速度剖面相差较大，主流区域相差较小，肋条结构的减阻效果主要基于近壁面；肋条结构将漩涡推离壁面，使肋底充满低速流体，降低近壁面处动量交换，减小摩擦阻力；与光滑壁面相比，尺寸为＝＝0.516 5 mm的肋条具有4.38%的减阻效果。

输气管道； 肋条减阻； 摩擦阻力； 数值模拟

目前，国际能源形势严峻，相关研究表明，美国能源消耗总量的16.00%用于克服运输过程中阻力，如果能够减阻50.00%，则每年可节约7.85%的能源[1]。天然气管道的主要损失为摩阻损失，因此减小摩擦阻力成为输气管道的研究重点[2]。其中，仿生肋条减阻作为一种能够有效减小壁面摩擦阻力的湍流减阻的方法，被认为在天然气管道运输中具有广泛的应用前景。

M.J.Walsh等[3⁃5]采用实验方法进行了平板肋条减阻研究，探究不同形状、不同尺寸肋条的减阻情况，建立了大量的数据库。J.R.Debisschop等[6]指出，与零压力梯度流场相比，肋条在存在逆压梯度流场的情况下减阻效果更好，减阻率为13.00%。D.C.Chu等[7]对V形结构肋条进行了数值模拟。结果表明，V形结构的肋条只能在转捩或完全发展的湍流流动中发挥作用。B.E.Launder等[8]、M.Benhlilou等[9]利用湍流模型探究肋条表面流体的流动情况，计算了近壁面流体的平均流速、雷诺剪切应力，计算结果与实验数据吻合较好，表明使用CFD工具可以准确地模拟肋条表面流体的流动情况。于洋等[10]在大管径输气管道中加装肋条进行数值模拟，研究了流体流动情况。李闯[11]采用大涡模拟方法，针对大管径输气管道进行了肋条减阻机理探究。

本文采用ANSYS⁃FLUENT软件，针对实际天然气管道，考虑实际加工难度，选择既定管道铺设三角肋条，对其湍流流场进行了大涡模拟，观察了肋条管道与光滑管道近壁处湍流边界层流动特性，分析了三角肋条的减阻效果及机理。

1 数值模拟

1.1 模型参数

考虑到天然气在实际管道中的流速，以低速流体在小管径中的应用作为出发点。从应用以及施工难度方面考虑，选择在光滑管道内铺设常见的三角形仿生肋条。选择内径为15.000 0 mm的管道，流速初定为7.5 m/s。

研究对象为圆管中的V形肋条，选用减阻效果较好的肋条深度与间距相等的肋条结构。

选择在既定规格的圆管内铺设仿生肋条，可铺设的肋条个数的表达式见式（1）。

式中，为肋条间距，mm；为被铺设管道的既定半径，mm；为可铺设的肋条个数。

经初步计算，得到铺设肋条的个数为＝85.20，取整后得到圆管内铺设肋条个数为85个。单个肋条对应的圆心角为4.235 3°。将肋条个数再次代入式（1），得到肋条间距＝0.516 5 mm，因此肋条高度为0.516 5 mm，无量纲化尺寸为+＝+＝10.0。

不同肋条的纵向突出高度示意图见图1[12]。图1中，A、B、C代表三种不同纵向高度的肋条结构。

图1　不同肋条的纵向突出高度示意图

从图1可以看出，当三角形肋条间距等于肋条高度时，肋尖距有效流源点的高度为：pl＝0.176。经计算得，肋尖提升高度＝0.090 9 mm。

肋条有效流源示意图如图2所示。图2中，为计算所得的有效半径，mm。经计算可知，肋条管道的有效直径（2）为14.148 8 mm。换言之，在既定工况下，内径为15.000 0 mm的光滑管道内铺设仿生三角形肋条，其有效直径为14.148 8 mm。

图2　肋条有效流源示意图

1.2 计算模型的确立

流体工质为天然气，甲烷温度为288.16 K，密度为0.648 kg/m3，动力黏度为1.106 7×10-5Pa·s。计算域采用整周光滑圆管和整周加肋管道。光滑圆管的几何模型：内径为14.148 8 mm，管长为75.0 mm。肋条管道选取内径为15.000 0 mm的天然气管道，管长与光滑圆管流向长度相同。整周肋条管道共铺设有85个肋条。光滑圆管及肋条圆管的几何模型如图3所示。

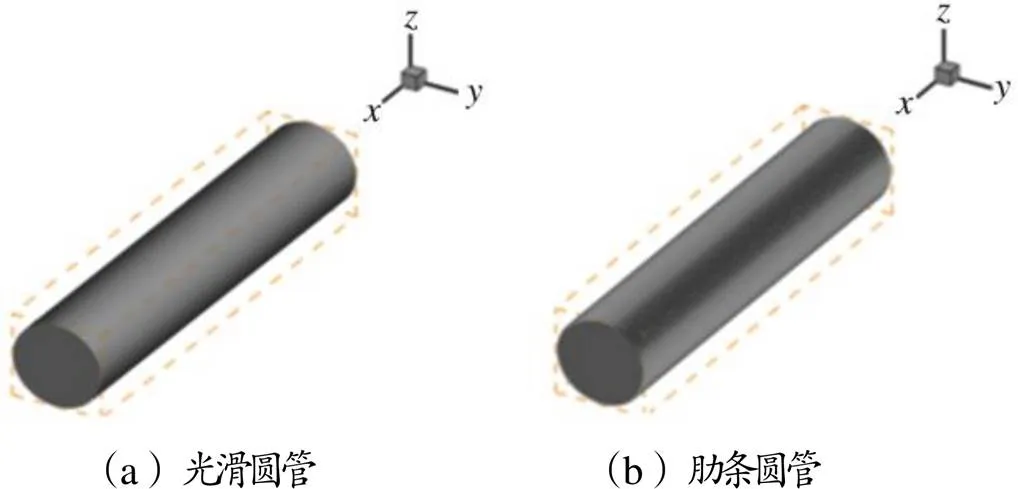
图3　光滑圆管及肋条圆管的几何模型

1.3 网格参数及计算条件设置

使用ICEM软件，对模型进行结构体网格划分。流向网格均匀分布，法向近壁处的网格需加密处理，且要控制网格的数量：第一层网格高度为0.01，且以1.01倍的网格尺寸增长率增长，以满足无量纲壁面距离为1。以壁面减阻率作为检验指标，进行网格无关性验证，结果见表1。由于算例2和算例3的网格计算结果误差相差很小，同时考虑到节约计算资源，采用网格量适中的方案即算例2进行计算。

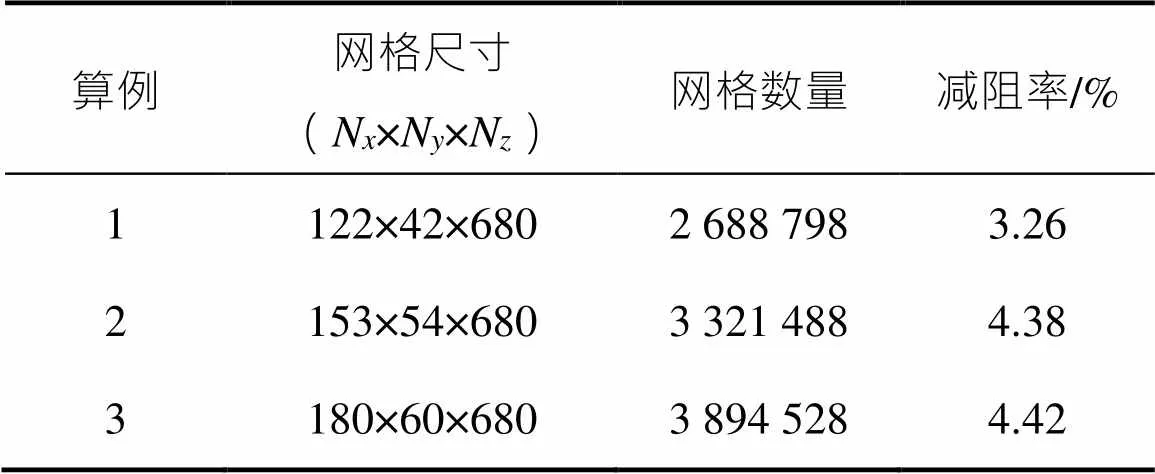
表1　网格无关性检验结果

光滑管道和肋条管道的网格划分如图4所示，肋条管道网格近壁区局部示意图如图5所示。

图4　光滑管道及肋条管道的网格划分

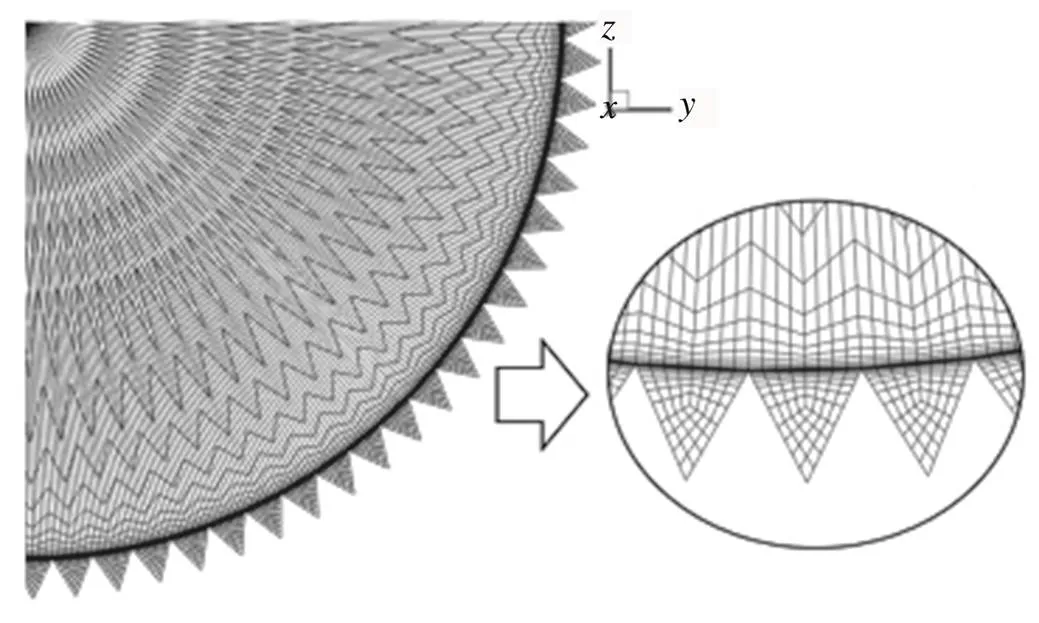
图5　肋条管道网络近壁区局部示意图

采用LES湍流模型进行非定常数值计算。压力速度耦合求解采用SIMPLE算法[13]，梯度求解采用基于单元的最小二乘方法，压力求解采用二阶格式，动量方程求解采用中心差分，时间离散采用二阶隐式格式。肋条壁面设为固壁无滑移，流向两个面设为平移周期性边界条件，给定质量流量为7.641 3×104kg/s。

LES模型选取Smagorinsky⁃lilly亚格子模型，模型系数采用默认值0.1。时间步长Δ＝0.05/l（l为槽内最大流速，m/s；为网格相邻节点间的距离，mm），其值为1×10-5s，对10 000个时间步的数据进行时间平均处理，获取统计数据。

2 计算结果及分析

2.1 时均结果分析

光滑管道及肋条管道的减阻数据见表2。分别提取了壁面上的平均剪切力，通过时均处理，比较后得到减阻率为4.38%。

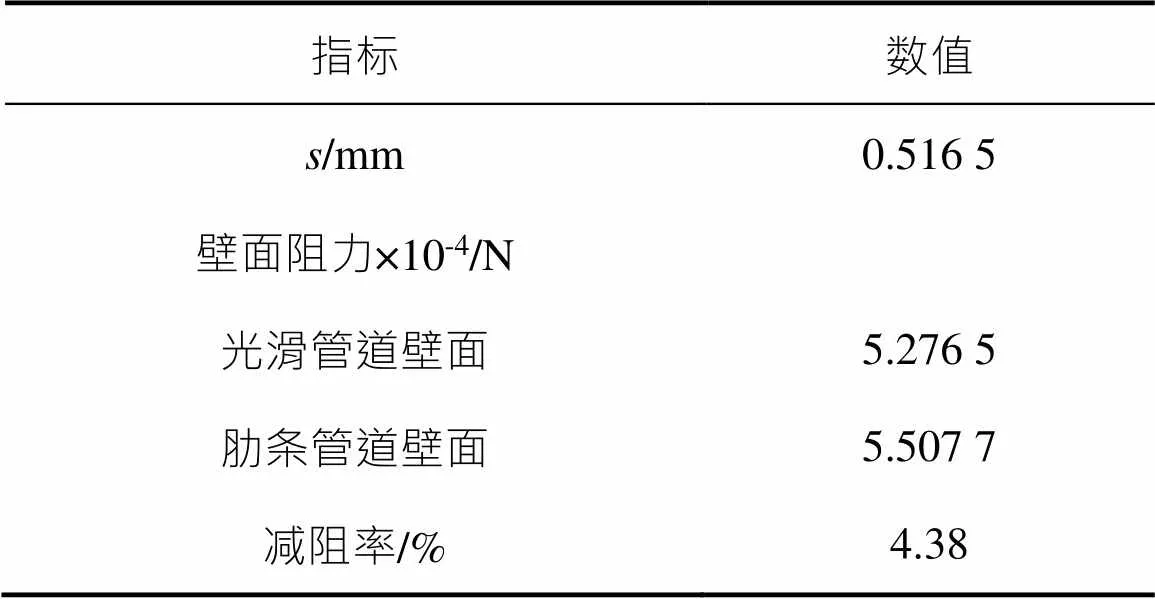
表2　光滑圆管及肋条管道减阻数据

将数值模拟得到的减阻率结果与理论计算值及前人的实验值[14⁃15]进行对比，结果基本吻合，证明了本文数值模拟方法的准确性。减阻率计算公式见式（2），减阻率计算结果对比如图6所示。

式中，为减阻率，%；为光滑管道壁面摩擦阻力，N；为肋条管道壁面摩擦阻力，N。

从流场中分别提取平均流向速度，对其进行无量纲化处理，通过时均处理得到光滑管道和肋条管道的流向速度分布，结果如图7所示。横坐标和纵坐标分别是通过摩擦速度以及运动黏度进行无量纲化处理得到的指标。

图7　光滑管道及肋条管道流向速度分布曲线

由图7可以看出，在近壁区，光滑管道和肋条管道有较大的差距。其中，相对于光滑表面，流体流经肋条结构表面时速度相对较大，而光滑管道近壁区的速度斜率较大，其速度梯度较大。由图7还可以看出，随着与壁面距离的增大，两条曲线逐渐贴合，在管道中心位置略有差异，这说明肋条结构减阻主要在近壁区，与主流区的关系相对较小。这一结果验证与成庆林等[16]的观点一致。

2.2 瞬时速度分析

在＝0.875 s时，光滑管道和肋条管道在流向截面＝0.037 5 m剖面处的瞬时速度分布云图如图8所示。从图8可以看出，瞬时速度沿着径向发生变化。其中，在圆管中心区域的瞬时速度较大，且速度变化较慢，而在壁面附近的瞬时速度变化较快。这与光滑管道和肋条管道的平均流向速度曲线相一致。

图8　光滑管道和肋条管道在流向截面x=0.037 5 m剖面处的瞬时速度分布云图

光滑管道和肋条管道近壁区局部瞬时速度分布云图如图9所示。其中，低速的蓝色区域是因为管道近壁区流体流动主要受黏性力的作用，导致在这一区域内形成黏性底层。由图9可以看出，在逐渐远离近壁区时，惯性力对流体的作用大于黏性力，雷诺应力占据主导地位，因此形成了湍流对数率区。相比于光滑管道，肋条管道铺设有足够的仿生肋条结构，当流体流经肋条结构表面时，低速流体充满整个凹槽，使近壁区的低速流体厚度大于光滑管道，而低速流体的存在使高速流体被抬升，肋条上方的高速流体流过凹槽内的低速流体，避免与壁面直接摩擦，此时凹槽内的“安静”流体起到了滚动轴承的作用，这也是肋条的一种减阻机理。

图9　光滑管道和肋条管道近壁区局部瞬时速度分布云图

2.3 流线图分析

光滑管道和肋条管道在近壁区的流线图如图10所示。剖面位置为＝0.037 5 m处。从图10可以看出，在近壁区主要为低速流体层，且在肋条近壁区低速流体层更厚，凹槽附近充满了低速流体。

图10　光滑管道和肋条管道在近壁区的流线图

相比于光滑管壁，流体流经肋条结构表面时，在沟槽上方形成流向涡。肋条管道近壁区局部流线图如图11所示。由图11可以看出，在近壁区，沟槽内充满着低速流体，槽内的涡数量较少，近壁区主要的涡基本都在沟槽外，这些涡旋的直径大于凹槽结构的宽度，因此无法进入沟槽内扰动槽内流体。肋尖附近的流体受高速流体的影响远大于肋底流体受到的影响，仿生肋条结构表面的主要阻力来源都在肋尖附近。仿生肋条结构可避免高速流体对壁面的直接扫掠，减少能量直接交换带来的损失。根据二次涡理论，仿生肋条结构限制高速流体在槽内的活动，通过将高速扰动流体推离沟槽，也就是将漩涡推离凹槽，使沟槽内主要冲满低速流体以及少量的涡，是仿生肋条结构产生减阻效果的重要原因。

2.4 涡等值面分析

在＝0.875 s时，光滑管道及肋条管道的瞬时涡等值面图如图12所示。通过准则计算并运用流向瞬时速度着色，图为＝－300 000时的等值面。

图11　肋条管道近壁区局部流线图

图12　光滑管道及肋条管道瞬时涡等值面图

由图12（a）可以看出，光滑管道中存在不连续的涡，这体现了湍流流场结构的间歇性，其中涡的抬升以及下降对壁面摩擦阻力产生较大的影响；光滑壁面涡较大，密度相对较高，其近壁区湍流活动也相应较多。

由图12（b）可以看出，肋条管道与光滑管道相反，在近壁区涡较小。这是因为受肋条结构的影响，其涡核相对较细小。

由图12（b）还可以看出，涡量主要集中在肋尖附近，在槽道内部几乎不存在涡，表明湍流活动被限制在凹槽以外的区域发展，这也是肋条在管道中减阻的机理。此外，涡的分布沿径向发生变化，靠近主流区中心的涡更尖锐，甚至呈现一定的锥形，湍流活动也相应减小，这一现象体现了肋条结构对大量涡旋发展的影响。

3 结 论

（1）仿生肋条结构在肋尖附近剪切力较大，在肋底剪切力较小。相比于光滑管道，肋条管道的摩擦力主要来源于肋尖，在相同工况下具有4.38%的减阻效果。

（2）仿生肋条结构限制了高速流体在槽内的活动，通过将高速扰动流体推离沟槽，也就是将漩涡推离凹槽，使沟槽内主要冲满低速流体以及少量的涡，是仿生肋条结构产生减阻效果的重要原因。

（3）以天然气为工质，选择常规天然气中低流速作为设计基准，结合实际加工难度，在既定管道铺设肋条，从而计算合适的肋条尺寸（肋条间距的实际无量纲值在最优的减阻性能附近）以及光滑管道的有效直径。在考虑实际情况的基础上进行模拟计算，得到了相对理想的减阻效果。

［1］ Wood R.Aerodynamic drag and drag reduction［C/OL］//41st Aerospace Sciences Meeting and Exhibit.（2012⁃11⁃11）［2021⁃04⁃20］.https：//doi.org/10.2514/6.1986⁃267.

［2］ 唐绍猛.V形肋条减阻技术在输气管道中的数值研究［J］.天然气与石油，2018，36（2）：12⁃18.

［3］ Walsh M J，Lindemann A M.Optimization and application of riblets for turbulent drag reduction［C/OL］//22nd Aerospace Sciences Meeting.（2012⁃08⁃17）［2021⁃04⁃20］.https：//doi.org/10.2514/6.1984⁃347.

［4］ Walsh M J. Riblets as a viscous drag reduction technique［J］.American Institute of Aeronautics and Astronautics，1983，21（4）：485⁃486.

［5］ Walsh M J.Effect of detailed surface geometry on riblet drag reduction performance［J］.Journal of Aircraft，1990，27（6）：572⁃573.

［6］ Debisschop J R，Nieuwstadt F T M.Turbulent boundary layer in an adverse pressure gradient：Affectiveness of riblets［J］.AIAA Journal，1996，34（5）：932⁃937.

［7］ Chu D C，Karniadakis G E.A direct numerical simulation of laminar and turbulent flow over riblet⁃mounted surfaces［J］.Journal of Fluid Mechanics，1993，250：1⁃42.

［8］ Launder B E，Li S P.On the prediction of riblet performance with engineering turbulence models［J］.Applied Scientific Research，1993，50（3⁃4）：283⁃298.

［9］ Benhalilou M，Kasagi N.Numerical prediction of heat and momentum transfer over micro⁃grooved surface with a nonlinearmodel［J］.International Journal of Heat & Mass Transfer，1999，42（14）：2525⁃2541.

［10］ 于洋，刘德俊.仿生肋条减阻技术在输气管道中的应用［J］.辽宁石油化工大学学报，2017，37（4）：23⁃28.

［11］ 李闯.输气管道仿生肋条湍流减阻特性数值模拟［D］.抚顺：辽宁石油化工大学，2019.

［12］ Bechert D W，Bruse M，Hage W，et al.Experiments on drag⁃reducing surfaces and their optimization with an adjustable geometry［J］.Journal of Fluid Mechanics，1997，338：59⁃87

［13］ 张子良，张明明，徐建中.肋条湍流减阻机理的研究［J］.工程热物理学报，2020，41（2）：335⁃341.

［14］ Dean B，Bhushan B.Shark⁃skin surfaces for fluid⁃drag reduction in turbulent flow：A review［J］.Philosophical Transactions：Mathematical，Physical and Engineering Sciences，2010，368（1929）：4775⁃4806.

［15］ Walsh M J. Turbulent boundary layer drag reduction using riblets［C/OL］//20th Aerospace Sciences Meeting.（2012⁃08⁃17）［2021⁃03⁃28］.https：//doi.org/10.2514/6.1982⁃169.

［16］ 成庆林，黄作男，孙巍，等.多相混输管道常温集输半径确定与应用研究［J］.石油化工高等学校学报，2020，33（2）：82⁃88.

Numerical Analysis of Drag Reduction of Riblet in Gas Pipeline

Xu Bing， Li Xiaoling， Wu Yuguo

（College of Petroleum Engineering，Liaoning Petrochemical University，Fushun Liaoning 113001，China）

With the wide application of clean energy, improving the transportation efficiency of gas pipeline has become a hot issue, among which, it is very important to reduce the friction resistance in the pipeline transportation process. In order to explore the application effect of triangular riblet in the drag reduction of gas pipeline, ANSYS⁃FLUENT software was used to numerically simulate the turbulent flow in smooth pipeline and riblet pipeline. The results show that: in the near wall area, the velocity profile of ribbed pipe and smooth pipe has a big difference, and the difference is small in the mainstream area. The drag reduction effect of riblet structure is mainly based on the near⁃wall surface. The riblet structure pushes the vortex away from the wall surface, filling the rib bottom with low⁃speed fluid, reducing momentum exchange near the wall surface and friction resistance. Compared with the smooth wall surface, the riblet structure with the size of＝＝0.516 5 mm has a drag reduction effect of 4.38%.

Gas pipeline； Drag reduction by riblets； Frictional resistance； Numerical simulation

TE832

A

10.3969/j.issn.1672⁃6952.2022.03.010

1672⁃6952（2022）03⁃0056⁃06

http：//journal.lnpu.edu.cn

2021⁃04⁃28

2021⁃06⁃01

辽宁省博士科研启动基金计划项目（2020⁃BS⁃227）；辽宁省自然科学基金指导计划项目（2019⁃ZD⁃0060）。

徐冰（1999⁃），女，硕士研究生，从事长输管道减阻方面的研究；E⁃mail：316206849@qq.com。

吴玉国（1977⁃），男，博士，教授，从事油气储运及相关技术方面的研究；E⁃mail：wyg0413@126.com。

（编辑 宋锦玉）