板框过滤实验中滤饼压缩性指数为负的原因分析
李保红,覃金舟,彭延文,韦 收,刘红菊
(大连民族大学 生命科学学院,辽宁 大连 116605)
过滤是在压力差推动下,固液混合物中的液体透过过滤介质,比如纱布和滤饼,而固体颗粒被截留,从而实现与液体分离的过程[1]。化工原理板框过滤实验要求学生掌握恒压过滤常数的测定方法,加深对相关概念和影响因素的理解;掌握滤饼压缩性指数s和物料常数k的实验测定方法。2020秋季学期,学生在过滤实验报告中计算出的滤饼压缩指数均为负数,明显与理论上该值应介于0~1相矛盾。关于滤饼压缩性指数s为负的文献报道有2篇:一篇是2011年朱金璇测量了以碳酸钙悬浮液为工作介质,进行恒压板框过滤(过滤压力分别保持0.1 MPa、0.2 MPa和0.3 MPa),得到s=-0.102 3,遗憾的是作者没有注意到滤饼压缩性指数为负与理论取值0~1相矛盾[2];另一篇是肖武等在2016年分析发现,由于学生的两个不正常操作(计量桶中液位调零用清水,被倒入滤浆槽和洗涤过程中滤饼损失),导致滤饼压缩指数为负数[3]。
本研究通过重复该实验,对得到的实验数据和结果进行分析,发现导致这一结果的可能原因,然后通过验证实验和理论分析确认,证实漩涡泵未及时清洗干净导致滤浆浓度随过滤过程的进行而发生了变化,是问题产生的真正原因,最终有针对性地完善了实验的操作步骤和注意事项。
1 实验原理
恒压过滤过程可用以下方程描述:
(q+qe)2=Κ(θ+θe)。
(1)
式中:q为单位过滤面积获得的滤液体积,单位m3·m-2;qe为单位过滤面积上的虚拟滤液体积,单位m3·m-2;θ为实际过滤时间,单位s;θe为虚拟过滤时间,单位s;K为过滤常数,单位m2·s-1[4]。
将式(1)对q进行微分可得:
(2)
θe由下式求出:
qe2=Kθe。
(3)
K=2k(Δp)1-s。
(4)
式中:s是滤饼压缩指数;k为滤饼特性常数;Δp是过滤的压差。式(4)两边取对数:
lgK=(1-s)lg(Δp)+lg(2k)。
(5)
因k为常数,故Κ与Δp的关系在双对数坐标系上表示时应是一条直线,直线的斜率为(1-s),由此可确定滤饼压缩指数s,代入式(4)求出滤饼特性常数k。
2 实验装置
实验装置(天津大学基础实验中心2005年制造)及实验流程如图1。滤浆槽内配有浓度在2%~4%的轻质碳酸钙悬浮液,使用电动搅拌器进行搅拌,使之混合均匀。所得滤液收集到计量桶内计量。正常过滤时,滤浆经阀门6流入旋涡泵,经泵加压后流入阀门1和2所在的水平管路,同时管路内的压力由压力表1显示;阀门2是全开的角阀,阀门1的开度用于调节循环回滤浆槽的料液量,从而调节过滤的压力使之保持在恒定值,因而阀门1和2是并联的关系。清洗旋涡泵时,阀门1和6是关闭的,自来水经阀门5进入旋涡泵,靠自身压力上升并通过阀门2进入板框过滤机的固定头后排空,清洗到排出的水清澈为止。
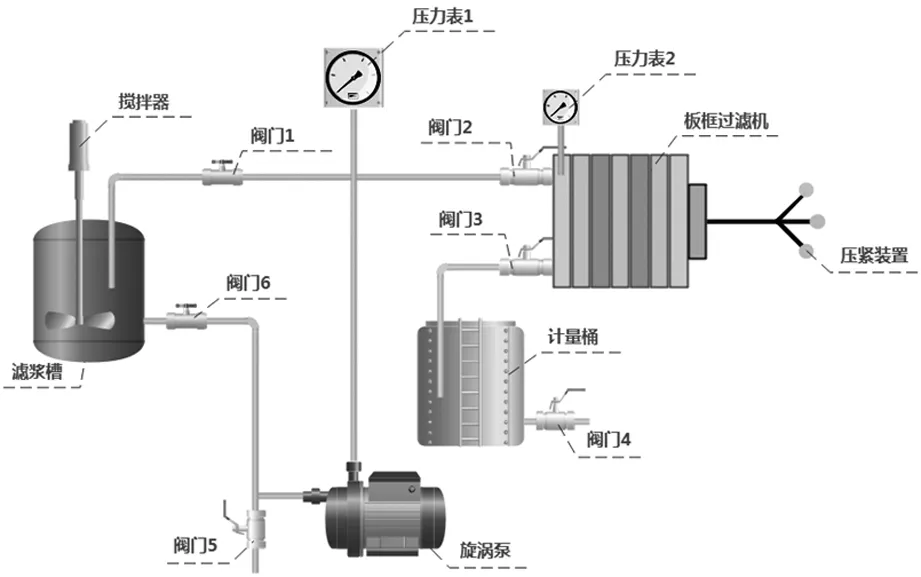
图1 恒压过滤实验流程
设备主要技术指标:过滤板:160 mm×180 mm×11 mm;滤布,工业用,总过滤面积0.047 5 m2;计量桶:长275 mm×宽322 mm。
3 实验步骤
(1)清洗板框和润湿滤布;
(2)开启电动搅拌器,搅拌均匀滤浆槽内浆液;
(3)板框过滤机安装顺序为:固定头-非洗涤板-框-洗涤板-框-非洗涤板-可动头,用压紧装置压紧后待用;
(4)全开阀门1和6,使阀门2和5处于全关状态,启动漩涡泵,调节阀门1使压力表1指示值保持在规定值不变;
(5)待压力表1指示值稳定后,先打开滤液出口阀门3,再打开滤浆入口阀门2,过滤开始。待计量桶内第一滴液体落下时,启动秒表连续计时,间歇性读数,记录滤液高度每增加20 mm所用时间,收集5组数据,滤液流出速度明显变慢后,记录滤液高度每增加10 mm所用时间,当累积增加的滤液高度达到160~180 mm时停止计时,并立即关闭阀门2;
(6)打开阀门1使压力表1指示值下降,开启压紧装置,卸下过滤框内的滤饼并放回滤浆槽内,用滤液将滤布清洗干净,再将计量桶内的滤液倒回滤浆槽内,以维持滤浆浓度保持不变;
(7)调节阀门1,改变过滤压力,从步骤3开始重复上述实验,至少需测量3个不同压力下滤液量随时间变化的数据;
(8)实验结束时,关闭阀门1和6,阀门5处接自来水,打开阀门2,对漩涡泵进、出口进行清洗,直至出水口流出的水变清澈[5]。
4 实验结果分析
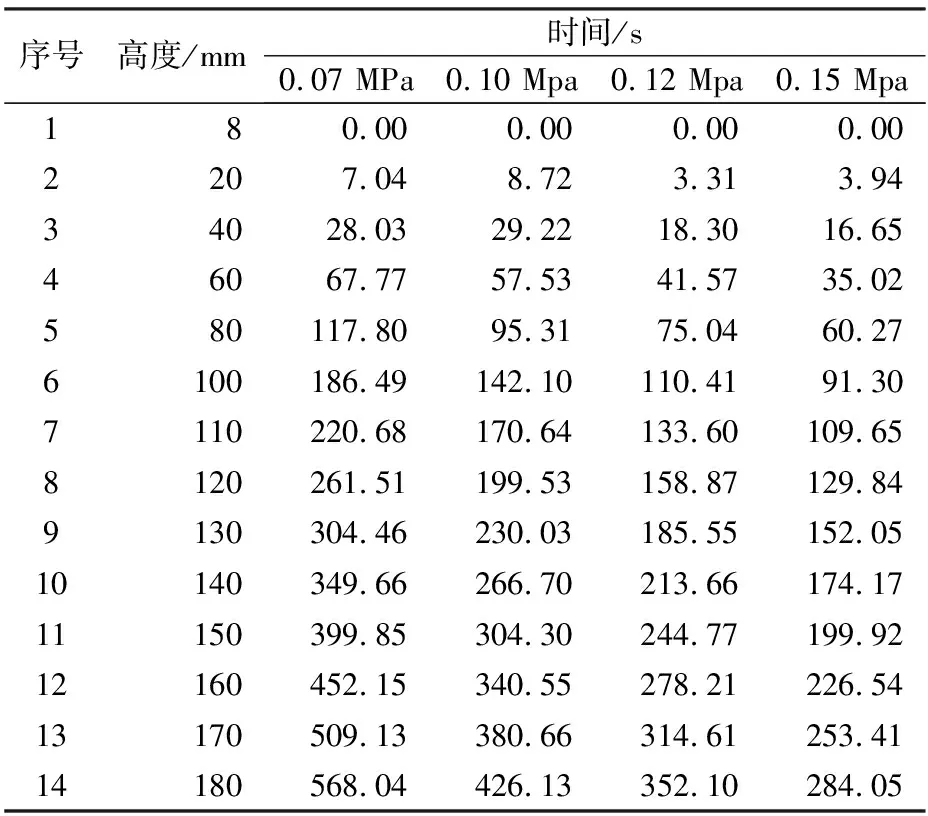
按照上述实验步骤,采用图1实验装置分别在三个不同恒定压差条件下进行实验,每组实验测定12~14个过滤时间θ和滤液累积量q。使用Excel 2019对测量数据进行处理,计算不同压差下过滤常数K、qe和θe,以及滤饼特性常数k和压缩指数s。2020秋季学期,所有学生得到的滤饼压缩性指数s均为负数,这与s理论值范围(0,1)不相符。重复该实验过程,以2021年1月14日的实验数据为例,原始测量数据记录见表1。

表1 恒压过滤实验原始数据记录(2021-01-14)
4.1 恒压过滤实验数据处理和结果分析
依据上述实验步骤,分别在过滤压差为0.05 MPa、0.10 MPa和0.15 MPa,过滤面积A=0.047 5 m2条件下进行过滤操作,得到12~14组滤液高度hi与过滤时间θi的原始数据,通过Excel 2019进行数据处理之后,以(Δθ/Δq)i为纵坐标,qav为横坐标作图,微分法得到的(Δθ/Δq)与(qav)i的关系图如图2。
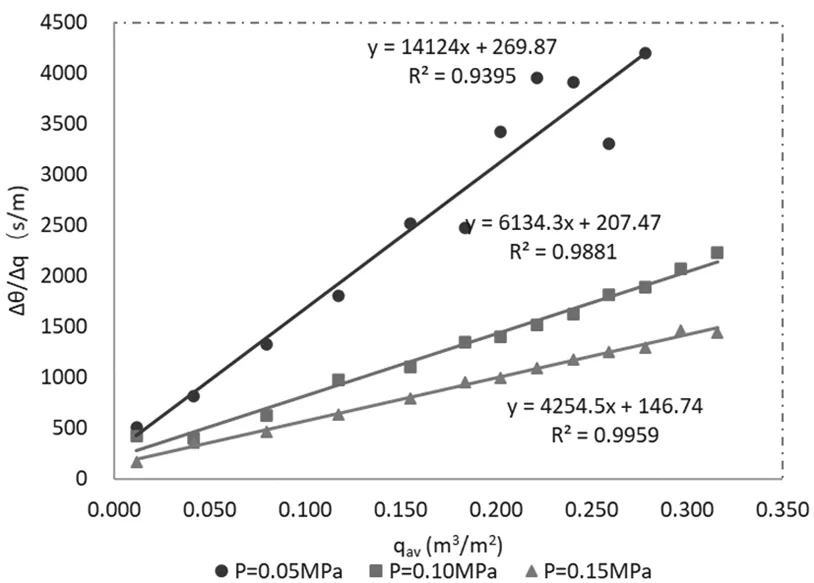
图2 微分法得到(Δθ/Δq)i~ (qav)i关系图
由图中直线的斜率和截距可计算出K、qe和θe,所得结果见表2。

表2 恒压过滤实验中得到的过滤常数
由表2中不同压差ΔP下对应的过滤常数K,在双对数坐标下作图,并通过幂回归得到K与压差ΔP的关系图式为y=9E-10x11041,R2=0.994 9。其回归方程的指数对应方程(4)中的(1-s),从而求得压缩性指数为-0.1041,物料常数k为4.5×10-10。
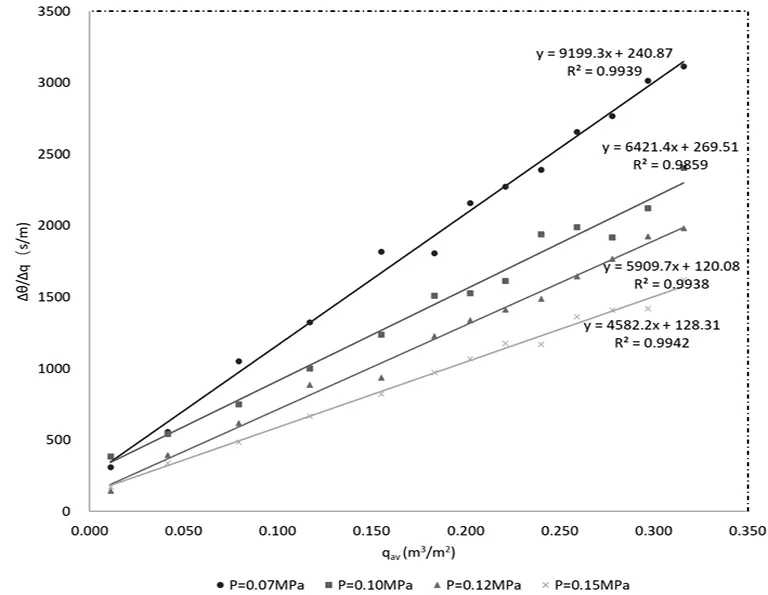
上述结果与学生的实验结果一致,虽多次重复实验过程,但得到压缩性指数s始终为负数。目前实验中的a为1.1041,已经超过理论值的上限。数据分析推断是由于随着压力增加,恒压过滤平衡常数Ki值也增加,但其增速高于式(4)右侧2k(ΔP)a(0 由于在实验过程中,发现压力表指针在0.05 MPa压力下摆动幅度过大,很难保持压力稳定。因此选择0.07 MPa作为最小过滤压差开始实验,依据前文所述实验步骤,测量4个不同的过滤压力(0.07 MPa,0.10 MPa,0.12 MPa,0.15 MPa)下的数据,同时通过改进实验操作步骤,消除以上干扰实验结果因素。具体措施:首先,在实验开始之前对漩涡泵进行清洗,使管道内部没有滤浆沉淀;然后,在每组实验结束后,拆装板框过滤机,将滤饼直接倒入滤浆槽,滤布放入滤液槽里洗涤,清洗完成后将滤液槽中的液体倒入滤浆槽,防止滤饼损失,保证滤浆浓度不变。通过严格执行上述实验操作步骤,得到新的实验数据和处理结果见表3。 表3 恒压过滤实验原始数据(2021-01-19) 以(△θ/△q)i为纵坐标,(qav)i为横坐标在普通坐标下作图绘制直线,如图3。 图3 微分法得到(Δθ/Δq)i~(qav)i关系图 由此计算得到过滤常数K,qe和θe,具体结果见表4。根据表4中数据,在双对数坐标系下,绘制过滤常数Ki随着不同压差ΔPi的变化线,所得到回归线y=1E-08x0.888 1。 由其回归方程的指数计算得到s=0.111 9,与理论值的要求相符。计算结果表明,严格执行改进的实验操作步骤,得到压缩性指数s为正数,且在合理范围之内。又进行多次重复实验,均得到了相同的结果,证实了结果的可重复性,也充分证明了以上对板框过滤实验中滤饼压缩性指数为负数原因的分析是正确的。 将式(2)从θ=0到θ进行积分并经整理(注意θ=0时,q=0)可得: (6) θ/q与q亦为直线关系,斜率为1/K,截距为2qe/K。由于实验测定的是θ和q值,根据式(6)可以直接用θ/q对q作图或者进行线性拟合,从而确定过滤常数K和qe,即用于实验数据处理的积分法[7-9]。由于积分法在使用简便性和结果精确度方面都优于微分法[9],因此可用积分法进一步提高处理结果的准确性。将上述实验数据用积分法进行处理,以(θ/q)i为纵坐标,qi为横坐标在普通坐标下作图绘制直线,如图4。 表4 验证性恒压过滤实验得到的过滤常数(微分法) 图4 积分法得到(θ/q)i~qi关系图 由此可以计算得到过滤常数K、qe和θe,计算结果见表5。 根据表5中所求不同压差下ΔPi的过滤常数Ki数据,在双对数坐标系上绘制得到回归线y=7E-09x0.929 6,R2=0.965 1。 表5 验证性恒压过滤实验得到的过滤常数(积分法) 由其回归方程的指数可计算得滤饼压缩指数s=0.070 4。因微分法需要对数据进行数值微分计算,此外,微分法将Δθ/Δq作为dt/dq的近似总是存在一定误差。积分法则不存在这种误差[9],因此积分法比微分法结果更精确,故该方法与微分法计算得到的压缩性指数s在数值上不一样是合理的。 上述分析推断和实验验证确定了恒压过滤实验中滤饼的压缩指数s为负数的主要原因是实验结束之前没有对旋涡泵进行清洗,因此,需进一步完善板框过滤实验操作,即做实验的第一步是清洗漩涡泵。此外,文献[9]指出过滤实验数据处理时采用微分法,不仅数据处理复杂,而且处理结果可能有比较明显的误差。因此,建议采用积分法进行实验数据处理。 通过对板框过滤实验数据的处理和分析,得到了滤饼压缩性指数s为负数的原因是漩涡泵中残留的CaCO3沉淀改变了滤浆浓度。即实验数据测量完成后,学生急于离开实验室,未能清洗管道中滤浆沉淀,导致实验过程随着操作时间的推移,滤浆浓度发生变化。基于此,改进实验操作步骤并进行实验验证,无论采用微分法还是积分法进行实验数据处理,均能得到压缩性指数s为0~1正数,与理论值的范围完全符合。改进的板框过滤实验操作步骤为获得正确的实验结果提供了保证,也为类似实验问题提供了分析与解决的思路。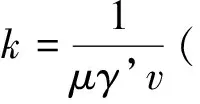
4.2 滤饼压缩性指数为负数原因的实验验证



4.3 改进实验步骤
5 结 论
——非均布滤饼的局部比阻与平均比阻的测定与计算方法

