一种流水车间预测性维护与生产调度集成优化方法
李杨,杨明顺,陈曦,韩周鹏,徐二宝,李言
(西安理工大学 机械与精密仪器工程学院,西安 710048)
生产调度和设备维护是制造车间的两项重要活动。生产调度是在可调配范围内,对各种资源进行合理分配,指定相应的设备并安排合理的加工顺序,使预期目标达到最优。实际生产中制定的生产调度计划往往难以达到预期效果,主要原因之一是在进行方案制定时未考虑机器设备性能的退化和故障维护[1]。机器设备运行过程中若发生故障将影响生产计划的正常执行。因此,考虑设备维护活动,将生产调度与设备维护调度结合集成优化已成为目前生产调度研究的热点问题[2-3]。
近年来,在生产调度与设备维护集成优化方面已有取得一些研究成果。Zhang等[4]在论文中证明了调度维护集成优化问题是一个NP-Hard问题,并利用启发式算法进行求解。Lu等[5]针对预防性维与生产调度集成问题,提出了一种基于最优调度特性的遗传算法,优化系统鲁棒性和稳定性。Fitouhi等[6]将非周期性预防性维护与多状态系统中的生产计划进行集成,以系统运行成本与维修费用最少为目标建立了一种生产与设备维修联合调度模型。黄剑秋等[7]给出一种描述生产负荷、预防性维护与生产计划提前期的关联函数,在此基础上建立了生产计划与预防性维护联合优化模型。Mosheiov和Sidney[8]提出维护周期性概念,即机器的维护活动应与机器的工作时间以及状态相结合,距离故障发生的时间越长,维护花费的时间成本越高。赵世雄等[9]针对单机情况下生产与维护联合优化问题,设计了一种循环迭代算法。Zhou等[10]通过对串行无重入的系统联合优化过程分析,建立了预防性维护和调度的联合优化模型。赵济威[11]提出单机生产系统的非等周期不完美预防性维护与生产联合优化策略,综合考虑生产价值、生产成本、生产延迟成本及各类维护成本等,构建了总利润率模型。张岳君等[12]构建了一种生产计划与预防性维护集成建模框架,建立了并行机系统生产计划与预防性维护联合决策的模型,避免设备的过度维护,减少固定维护成本。
预防性维护是有目的、有计划地对设备进行检查、保养甚至更换的定期维修方式,而预测性维护是利用设备监测工具对设备运行状况实施周期性或持续监测,对监测信息进行分析、与既定数据、经验数据、检测故障发生前的机械状态进行比较,预测故障发生的时间,通过机器学习等技术评估设备状况,根据设备状况采取不同的维护活动,可以避免设备维护的盲目性,降低设备维护成本[13-14]。随着工业物联网技术在企业的广泛应用,设备维护方式逐渐预防性维护转变为预测性维护。
为了满足工业互联网环境下流水车间设备预测性维护,解决设备预测性维护引起的生产调度管控困难的现状,本文提出一种流水车间设备预测性维护与生产调度集成优化方法,给出一种新型维护策略,以机器发生故障时所属的状态区作为维护活动的决策依据;考虑设备预测性维护活动,以加工时间最小为目标,建立设备预测性维护与生产调度集成优化数学模型,设计一种改进的蝙蝠算法求解所建立的数学模型。通过本文方法可以有效解决流水车间设备预测性维护活动,降低设备维护工作量与成本,减少生产时间浪费与延误。
1 流水车间预测性维护与生产调度集成模型
1.1 问题描述
预测性维护也称为状态维护,是在机器的生命周期内,将运作状态作为维护时机控制标准,为避免机器停机而进行的提前维护活动。预测性维护作为一种新型的维护策略,针对机器的故障点难以捕捉的问题,通过采集的数据进行监测,建立故障预测模型,预测机器的工作状态参数,并根据预测结果对机器健康状态分类,深入分析机器故障的规律,对机器的故障发生时间做出预测并提前安排维护活动[13]。
本文在建模过程中,假定针对特定的车间设备,已经建立基于物联的机器状态数据采集装置,并建立了相应的故障预测模型[14]。针对发生故障的设备,所采用的维护策略是设备小修和视情维护的混合维护策略。根据采集的设备状态数据及响应的预测模型,将设备状态划分为四类区间:优秀、良好、不良、危险。机器执行车间加工任务,机器故障率会随着加工时间增大,根据待加工件的加工时间预测机器状态,根据预测结果对机器活动做出决策。若故障率超过规定的阈值,且机器状态为不良及以下,必须进行维护活动,根据维护活动的等级,使故障率进行不同程度的衰减;若进行正常加工,则每一次加工之前均需对机器状态区间进行预测。预测性维护过程如图1所示。
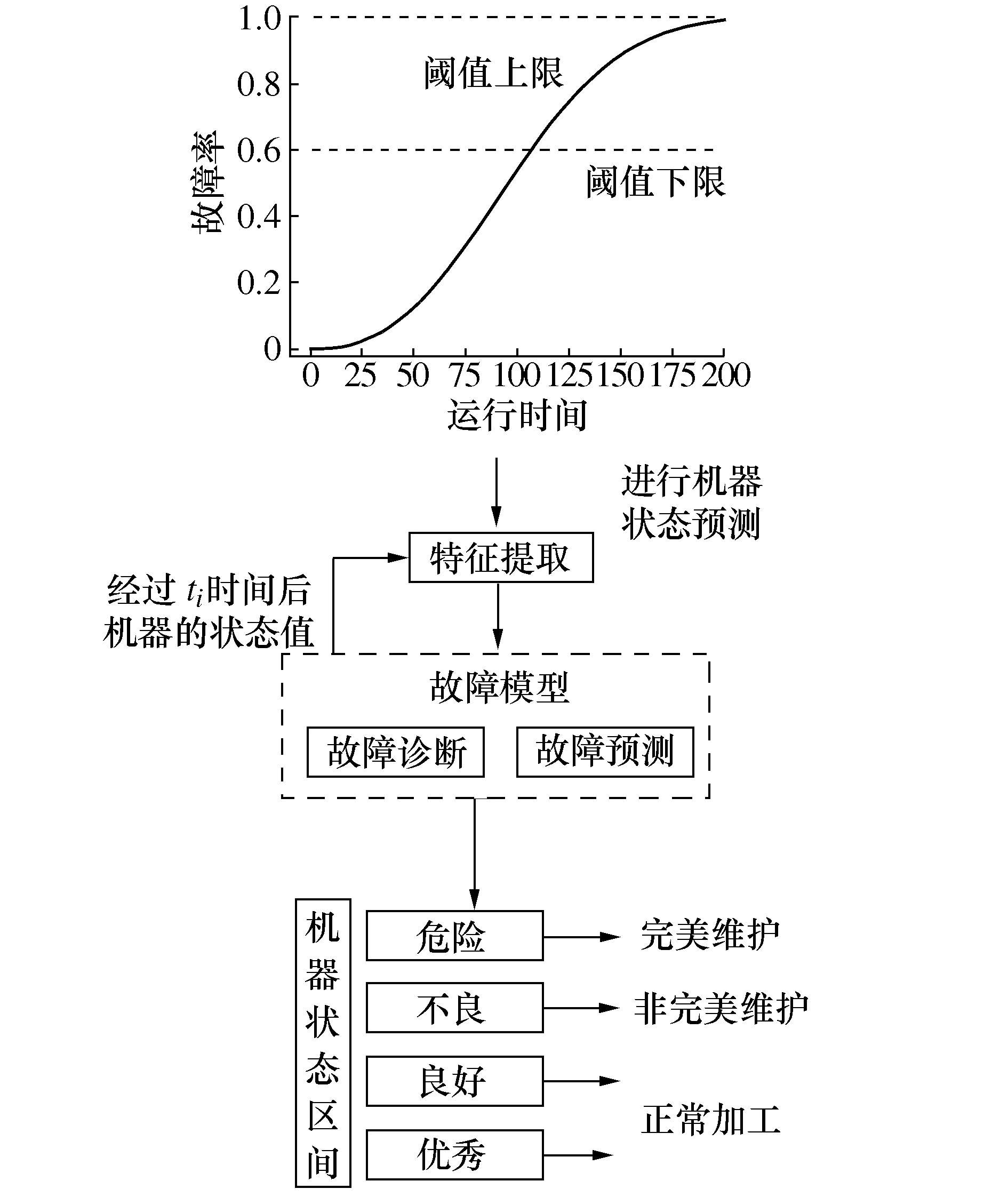
图1 预测性维护过程
针对流水车间,定义集合J,M,其中J表示工件集,M表示机器集,每台机器负责加工不同的工序,每一种工件的加工工艺路线相同,每一台机器加工的工件顺序不固定。在加工过程中满足:1) 零时刻,所有待加工件都已到达车间;2) 机器故障率分布符合威布尔函数;3) 加工过程中不可被中断;4) 维护活动结束后可立刻进行加工;5) 故障维护时间固定不变。
1.2 符号及参数
为了建立车间生产调度与预测性维护集成模型,定义变量参数如表1所示。

表1 变量参数表
1.3 模型建立
考虑到整个车间的预测性维护情况,建立以加工时间最小为优化目标的数学模型。
机器Mm有效的加工时间Tm1为
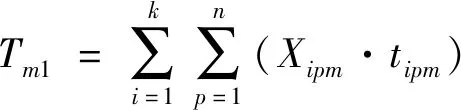
(1)
机器Mm的等待时间Tm2为
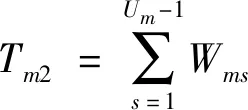
(2)
机器Mm的维护时间Tm3为
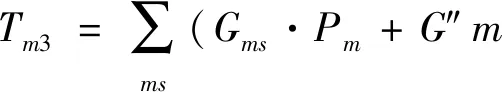
(3)
机器Mm的总加工时间Tm为:
Tm=Tm1+Tm2+Tm3
(4)
(5)
加工总时间T为
T=max{Tm|m=1,2,…,q}
(6)
以加工时间最短为目标,故最终目标函数Tmin表示为
Tmin=min max{Tm|m=1,2,…,q}
(7)
1) 预防性维护
工序Ji加工前,若机器故障率超过阈值,则对机器进行预测,根据结果安排机器维护活动。维护活动等级为
(8)
式中:g代表优秀;b代表良好;bk代表不良;r代表危险。
2) 约束条件
针对车间实际加工情况,给定以下加工约束:
(1)保证工件同时仅能在一台机器进行加工
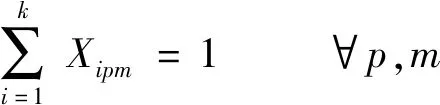
(9)
(2) 一台机器一次只能加工一个工件
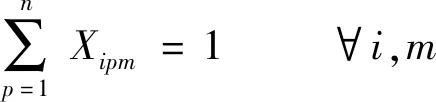
(10)
(3) 机器一次只能进行一种维护活动

(11)
(4) 机器加工开始时间不得小于机器维护活动结束时间

(12)
机器在加工过程中不可中断

(13)
(5) 机器1的第一个加工位置初始加工时间
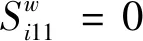
(14)
(6) 机器的加工起始时间不得小于该机器上一个加工工序的结束时间
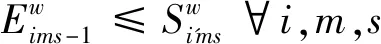
(15)
(7) 加工开始时间不得小于该工件在上一台机器的结束时间
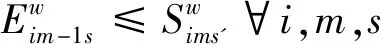
(16)
2 模型求解的蝙蝠算法设计
2.1 算法流程
蝙蝠算法是基于群体智能的启发式搜索算法,其核心思想是蝙蝠周期性向周围发射声波,当发现周围的猎物时,会改变声波的大小,以确定猎物位置。蝙蝠算法具有过程简单、准确性高、收敛速度快等优势[15]。算法初始化为一组随机解,通过迭代搜寻最优解,且在最优解周围通过随机飞行产生局部新解,加强局部搜索。每一次蝙蝠进行猎物搜寻时,所在的位置和速度都要进行更新。在t时刻蝙蝠的位置和速度表示如下:
ft=fmin+(fmax-fmin)·α
(17)
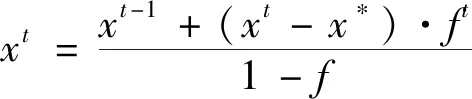
(18)
vt=vt-1+(xt-1-x*)·ft
(19)
式中:ft为脉冲搜索值;α为[0,1]内服从均匀分布的随机数;xt为当前蝙蝠位置;vt为当前蝙蝠飞行速度;x*为当前时间的最优解。
当蝙蝠发现新解时,音量A0开始衰减,同时脉冲发射率r逐渐增强。蝙蝠每进行一次寻优,音量和脉冲发射率进行一次迭代更新,即:
(20)
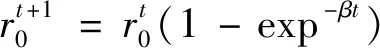
(21)
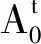
每产生一次新解,音量A0和脉冲发射率r进行一次更新,使得算法结果逐渐收敛。关键参数α,β的取值区间通常为[0.8,0.9]。为保证算法的高效性,音量衰减系数α更新表达式为
(22)
算法初始,α选定在相对较小的范围内,保证算法的全局搜索能力。算法中期,α选择较大值,保证算法的局部搜索能力,使得最优解的逼近速度增强。通过改进音量衰减系数更新,既保证了前期算法能够拥有足够的搜索能力,快速锁定最优解所在区域;也保证了后期的局部搜索能力,提升搜索速度与精度,能够最快地找寻最优值,不至于陷入局部最优。蝙蝠算法流程如图2所示。
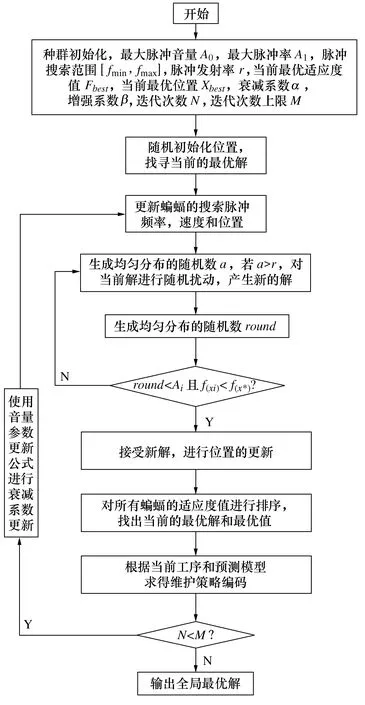
图2 改进蝙蝠算法流程
步骤1 初始化种群,给定初始值、最大音量A0、最大发射频率A1、脉冲搜索范围[fmin,fmax]、脉冲发射率r、音量衰减系数α、频率增强系数β、适应度值F、当前迭代次数N、最大迭代次数M、当前最优解适应度值Fbest以及当前最优位置Xbest。
步骤2 采用随机生成样本的方法产生初始种群,确定当前位置,寻找当前位置最优解。
步骤3 根据适应度函数确定种群中个体的最优适应度值Fbest。
步骤4 利用式(17)~式(19),更新蝙蝠速度和位置,得到新解和对应的适应度值解Fnew。
步骤5 若Fnew≥Fbest,则进行步骤6,否则执行步骤4。
步骤6 对当前解的位置适应度值进行判断。若当前适应度值更优,即Fnew≥Fbest,则当前适应度值成为最优适应度值,当前解成为目前最优解。
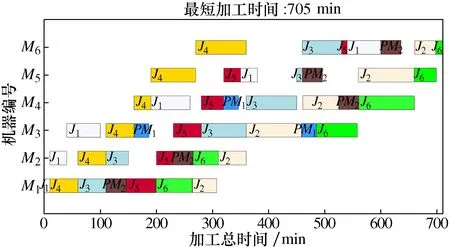
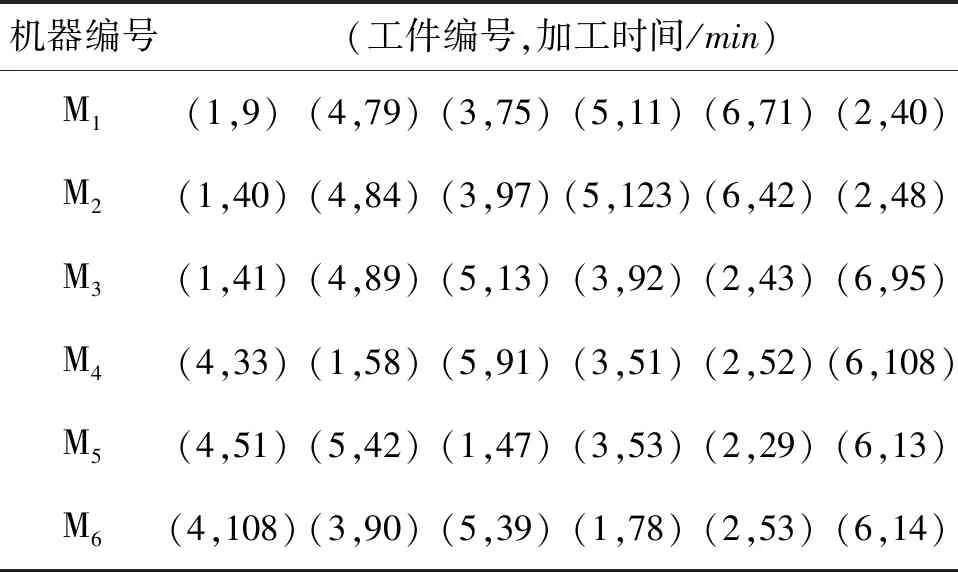
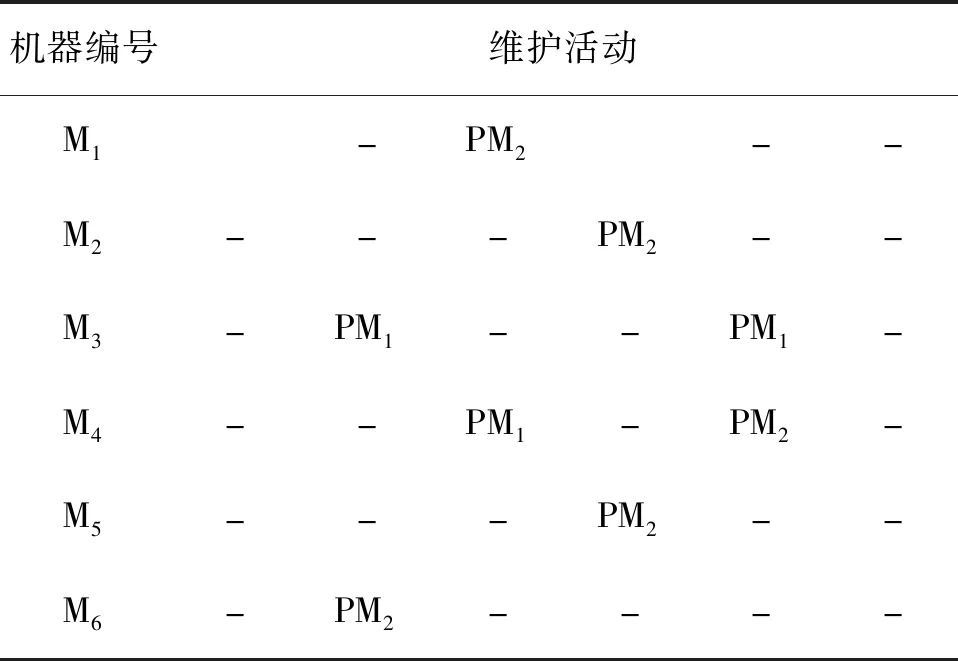
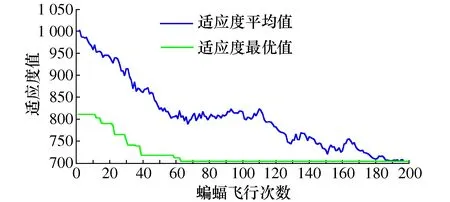
步骤7 生成均匀分布的随机数round,并计算当前解的标准差σ。若σi-σi-1 步骤8 若N 2.2 编码解码 在蝙蝠算法求解问题的过程中,确定算法的基础编码、解码规则是基础工作。编码是蝙蝠算法中确定蝙蝠位置和速度的基础。蝙蝠算法的编码是连续型编码,而车间生产调度优化则需要进行离散型编码。因此需要对算法的编码机制进行调整,以便能够适应生产调度。 本文选择工序和蝙蝠位置对应的方式进行编码,工件的工序和编码进行一一对应。编码分过程为2阶段: 1) 蝙蝠位置编码,将个体位置的大小定义为工件的工序,首先根据蝙蝠的位置进行编号,然后将位置按照从小到大的顺序依次排列,然后再次寻找到当前对应位置的工件编号,实行工件的编码排序,如图3所示。 图3 编码示意图 2) 维护策略编码,0表示不进行维护,1表示进行非完美维修,2表示完美维修。例{0,1,0,2,0,0},表示在加工完第一个工件之后进行小修,在加工完第二个工件后进行正常的维护操作。 对蝙蝠进行编号,每一次蝙蝠发生位置改变,记录当前位置并进行新一轮排序,得到当前工件加工顺序,直至算法寻得最优解,对应可求得当前最优工件加工顺序。 编码规则分为两层,初始解的生成也分为两层进行。本文采用拼接法生成初始种群:随机生成M个搜索范围内的数据,M表示当前的工件数量,以此表示当前初始情况的解;将这些数据分别对应各个工件的编号。再对这些数据按照从小到大的排序进行排列,将排列之后的数据顺序与工件加工序列相匹配,作为工件初始加工序列。之后每一次蝙蝠飞行之后,均按照此方法对蝙蝠进行编码、解码。 2.3 适应度函数 个体适应度是衡量个体在种群中优势程度的一种手段。适应度函数也称评价函数,主要是对个体的优劣性进行评估,并作为算法更新迭代的依据。 优化模型中目标函数F是完成加工时间的最小化,是极小值问题,将目标函数取负,设计适应度函数为 (23) 在适应度函数中加入选择压力系数,在进化过程中,使得非优个体仍有被选择的可能,保持了种群的多样性和搜索的收敛性,ε的取值范围约为[0.95,1)。 假定有6组待加工工件,J={J1,J2,…,J6},每个工件有6个加工工序;6台加工机器,M={M1,M2,…,M6}。加工车间为非置换流水加工车间,工序加工流程固定,加工时间如表2所示。 表2 工件加工时间信息 机器故障率阈值D[e]设为0.7,故障率函数分布服从Weibull分布,Weibull参数β=3.738,η=927.535,即 (24) 根据机器的加工状态进行分类,将机器的维护分为两个等级PM1(完美维护)和PM2(非完美维护),根据机器运作情况进行不同的维护活动。维护时间分别为30min和40min。 利用本文所建立的数学模型与设计的算法,建立本实例对应的数学优化模型,并采用Pythonmatplotib进行算法实现,验证了该方法的有效性与可行性。其中,初始化种群规模为100,迭代飞行次数为200。通过10次实验,最终的输出调度甘特图结果如图4所示,其中蓝色为进行一级维护PM1,浅紫色为二级维护活动PM2。 图4 甘特图 解码后最短加工时间为705min,最优车间调度序列及维护任务安排如表3和表4所示。 表3 最优工序调度 表4 维护任务安排表 图5为算法迭代过程中适应度值曲线。 图5 适应度值曲线 由图5可以看出,整个算法呈收敛状态,在蝙蝠位置更新次数达到约65次时,适应度值到达稳定状态,此时算法达到最优。本文所提方法在生产调度过程中综合考虑了流水车间设备预测性维护因素,不仅有效缩短了作业加工总时间,更加合理利用机器的有效工作时间,也极大地降低了设备维护活动量与维护成本。 本文提出一种流水车间设备预测性维护与生产调度集成优化方法,以解决车间物联网环境下设备预测性维修与生产调度问题。以机器发生故障时所属的状态区间为维护活动的决策依据,考虑机器完美维护和非完美维护两种维护方式,通过在生产调度过程中考虑设备的预测性维护,建立以加工时间最小为优化目标、融合设备预测性维护的生产调度数学模型;设计蝙蝠算法对建立的集成调度模型进行求解,对蝙蝠算法的音量衰减系数进行改进,并对蝙蝠算法中编码规则、适应度函数以及初始种群的选取进行设计分析,设计的改进启发式蝙蝠算法可以有效求解该调度优化模型。通过所提方法,可以有效减少流水车间生产调度中时间延误、资源浪费,同时降低了设备维护成本与维护工作量。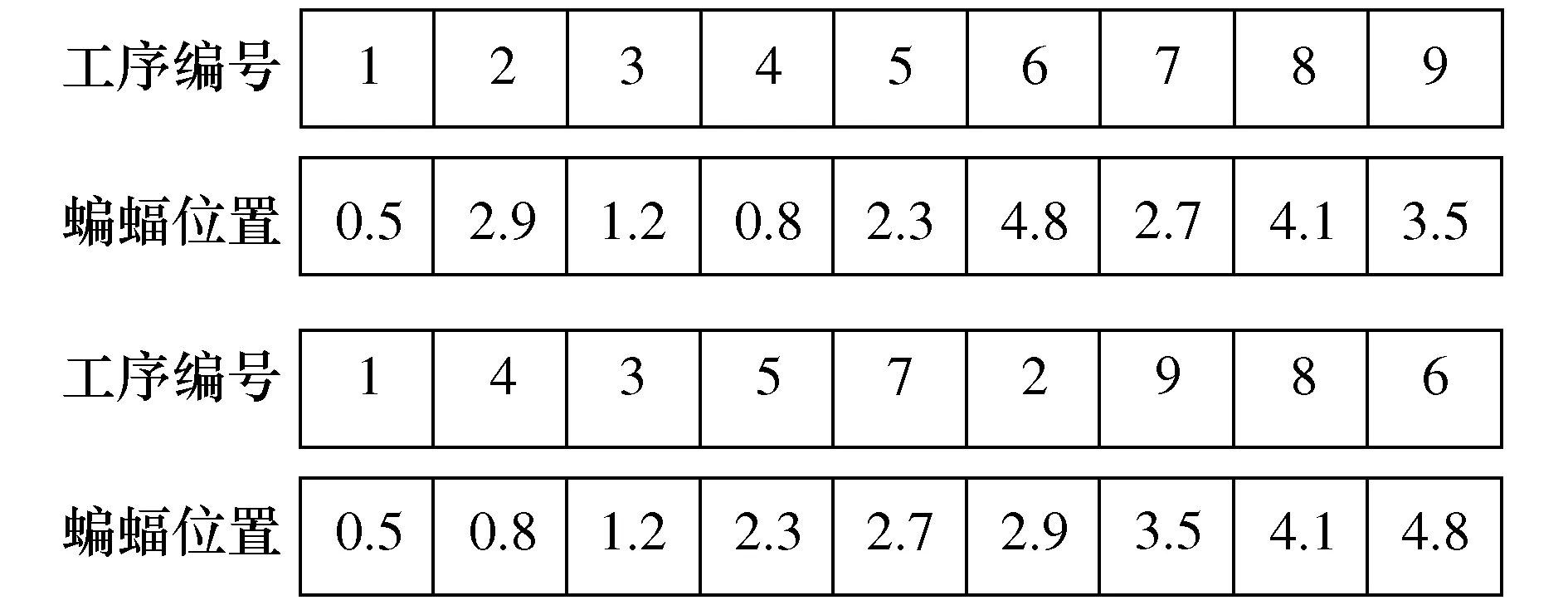
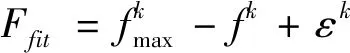

3 实例分析

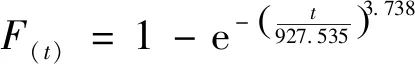
4 结论

