“圆”来如此，用”四点共圆”巧解中考题

樊启维

摘要：四点共圆在圆内接四边形综合问题的求解中占据了重要地位，都是在大题中结合题目的几何背景进行综合考查，重在考查学生对知识的应用能力.考查的基本类型有：利用四点共圆证相似，利用四点共圆求最值，这些问题大都利用转化思想，将几何问题转化为四点共圆问题，使题目能简单求解.

关键词：中考;四点共圆;相似;轉化

四点共圆在圆内接四边形综合问题的求解中占据了重要地位，都是在大题中结合题目的几何背景进行综合考查，重在考查学生对知识的应用能力.考查的基本类型有：利用四点共圆证相似，利用四点共圆求最值，这些问题大都利用转化思想，将几何问题转化为四点共圆问题，使题目能简单求解.

一、方法提炼

1.四点共圆定义.

如果同一平面内的四个点在同一个圆上，则称这四个点共圆，一般简称为“四点共圆”.

2.四点共圆的性质

（1）共圆的四个点所连成同侧共底的两个三角形的顶角相等.

（2）圆内接四边形的对角互补.

（3）圆内接四边形的一个外角等于它的内对角.

3.四点共圆的判定

（1）用“角”判定：

①一组对角互补的四边形的四个顶点在同一个圆上;

②一个外角等于它的内对角的四边形的四个顶点在同一个圆上;

③如果两个三角形有一条公共边，且位于公共边同侧的两个角相等，则这两个三角形的四个顶点在同一个圆上.

（2）“等线段”判定：

四顶点到同一点的距离相等，若OA=OB=OC=OD，则A，B，C，D四点共圆.

（3）用“比例线段”判定：

若线段AB，CD（或其延长线）交于点P，且PA·PC=PB·PD，则A，B，C，D四点共圆.

二、典例分析

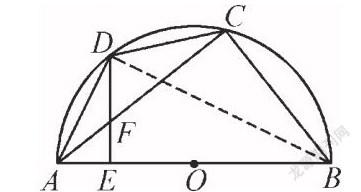
典例1.（2019年潍坊市）如图，四边形ABCD内接于半圆O，AB为直径，AD=CD.过点D作DE⊥_AB于点E.连接AC交DE于点F.若sin∠CAB=，DF=5，则BC的长为

【分析】连接BD，如图，先利用圆周角定理证明∠ADE=∠DAC得到FD=FA=5，再根据正弦的定义计算出EF=3，则AE=4，DE=8，接着证明△ADE∽△DBE，利用相似比得到BE=16，所以AB=20，然后在Rt△ABC中利用正弦定义计算出BC的长.

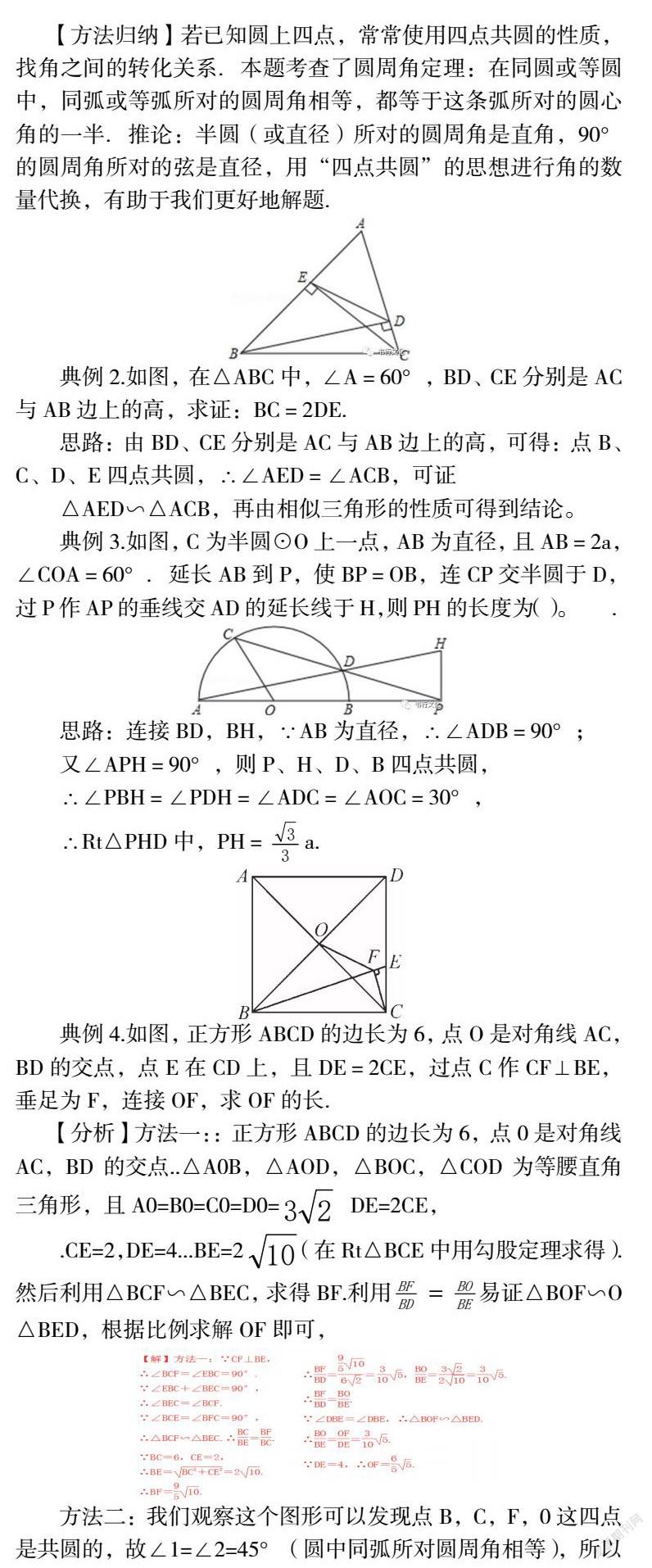
【方法归纳】若已知圆上四点，常常使用四点共圆的性质，找角之间的转化关系.本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半.推论：半圆（或直径）所对的圆周角是直角，90°的圆周角所对的弦是直径，用“四点共圆”的思想进行角的数量代换，有助于我们更好地解题.

方法二：我们观察这个图形可以发现点B，C，F，0这四点是共圆的，故∠1=∠2=45°（圆中同弧所对圆周角相等），所以∠1=∠3=45°，加上公共角∠DBE，就能得到△B0F∞△BED，这样的方法是利用几何图形中的变换得到所要的结论，少了许多计算.这道题的方法还有很多，还可以过点0向BE作垂线，垂足为M，然后利用勾股定理求解.

[方法归纳]：求线段长常用的方法就是两种：利用相似中的比例线段求线段长或者利用直角三角形中的勾股定理求线段长，

归纳小结：有些中考题利用四点共圆的方法解答，可以使思路更清晰，解答过程更加简洁。