基于LMD和ABC优化KELM的故障诊断方法

杨静宗，施春朝，杨天晴，吴丽玫

(保山学院 大数据学院，云南 保山 678000)

在矿物管道输送的过程中，其核心执行及唯一的动力机构是往复式高压隔膜泵，它是整个系统能否在安全、高效的前提下保持正常运行的保证，需要重点监测和维护。其中，单向阀是高压隔膜泵中的重要部件之一。由于在整条管线输送系统需要保持较高的输送压力和较长的年输送时间的情况下，单向阀需要持续不断地开启和闭合，这使得单向阀的磨损率、故障率和更换率一直处于较高的状态，其成为了高压隔膜泵中较易受损的零部件。因此，需要及时地判断其运行情况，防止其因为故障而损坏隔膜泵。

机械设备组件的故障通常伴随着振动信号的变化，通过对振动信号的监测是提高可靠性和安全性的一种有效方法。由于单向阀的运行是一个复杂的非平稳动态过程，单一的时域和频域信号无法有效地进行故障诊断，因而对振动信号的特征提取在整个单向阀的故障诊断中起到十分关键的作用。当单向阀发生粗颗粒卡住阀门造成单向阀关闭不严或者由于机械损伤而导致单向阀发生磨损击穿故障的时候，其振动信号有着多载波调制特性，所以在对信号进行解调或处理之前，对信号进行分解是一个必要的过程。常用的分解方法包括小波或小波包分解[1-2]、经验模式分解(EMD)[3]、集合经验模式分解(EEMD)[4]、局部均值分解(local mean decompoition，LMD)[5]等。LMD方法是一种新的自适应非平稳信号分析方法，最初由 Smith提出并应用于脑电图的频谱分析之中，较之STFT、小波变换等方法具有更好的自适应性，且和EMD相比，在迭代次数和抑制端点效应上的表现更佳[6]。LMD算法可以将复杂的非平稳信号分解为若干个PF分量，并且所有的PF分量均为对应的瞬时幅值与纯调频信号相乘而求得的，能够较好地保持信号的频率和包络信息。

排列熵(permutation entropy,PE)[7]作为一种测量动力学突变行为的非线性定量描述方法，有着计算效率高、抗噪声干扰、适宜在线监测等优势[8]。近年来，其已逐渐在机械设备的故障诊断中崭露头角。程军圣等[9]将排列熵应用到滚动轴承振动信号的故障特征提取中，并通过仿真实验证实所提出的方法是有效的。丁闯等[10]利用局部均值分解和排列熵相结合的方法对齿轮箱的故障信号进行分析，结果表明，求解其排列熵可以有效地表征齿轮箱的故障状态。石志标等[11]为了提升汽轮机转子故障的识别精度，从实验数据中提取排列熵特征，结果证实，所提出的方法在区别各种故障类型方面有着较好的优越性。

在常用的识别方法中，神经网络作为一种性能优良的人工智能方法，在故障诊断领域获得广泛的应用。虽然通过网络本身的自组织、自学习能力能够实现较好的分类，但在训练期间容易陷入过学习、陷入局部极值，并且需要大量的故障样本是其在现实应用中比较棘手的问题[12]。Huang等[13]在极限学习机(extreme learning machine,ELM)的基础上经过改进，并提出核极限学习机(kernel extreme learning machine,KELM)。其不但保证网络具有很好的泛化性能，而且引入核函数非线性映射处理来代替传统随机映射的方式实现线性可分，从而有效地改善模型识别的精度。然而，由于核函数的存在，参数设置情况将直接关系到识别性能的优劣。人工蜂群算法是近年来兴起的一种群智能算法，其通过模仿不同蜜蜂之间在采蜜的过程中的协作行为，并进行信息的交互与分析，从而达到找到最优解的目的。目前，其已应用于诸多优化问题之中，并取得较好的效果。

基于此，本文将采用人工蜂群算法对KELM的参数展开优化的方式进行建模，并应用到单向阀的故障诊断中。即通过LMD对信号作出预处理，以此来提取通过LMD分解后得到的特定PF分量中的排列熵作为特征量输入至ABC算法优化后的KELM分类模型中，以此展开单向阀的故障诊断。

1 算法基本原理

1.1 排列熵

排列熵是一种用来度量一维时间序列的复杂性与随机性的方法。与其他的熵相比，排列熵的优势较多，在计算效率、抗干扰性能等方面均有着较好的效果。通过运用熵的思想来对信号展开排列，有效地避免了非线性信号的失真问题。其基本原理如下。

假定时间序列{x(i),i=1,2,3,···,n}，对其作出相空间重构，将可以获得

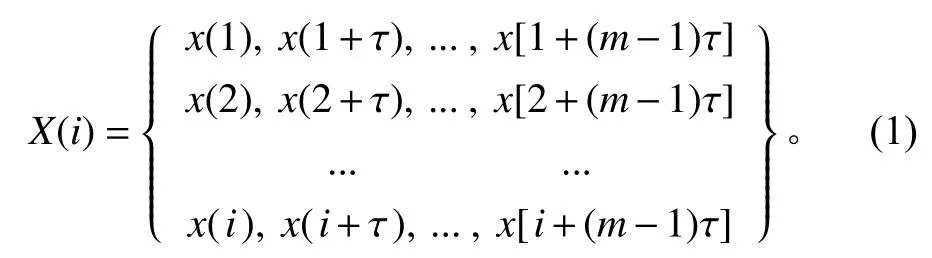
其中，m是嵌入的维数；τ 为延迟时间；j=1,2,···,k。上述矩阵的每一行均可以视为一个重构分量。

将X(i)={x(i),x(i+τ),···,x[i+(m−1)τ]}按照升序重新展开排列

假设x[i+(jp−1)τ]=x[i+(jq−1)τ]，并且p≠q，那么根据jp和jq值的大小展开排序。如果jp＜jq，那么x[i+(jp−1)τ]＜x[i+(jq−1)τ]。所以，对于任何的一维向量都可以得到一组唯一的序列

式(3)中，l=1,2,3,···,k，并且k≤m!。m维相空间映射不同的符合序列(j1,j2,···,jm)一共有m!种，S(l)为其中的一种排列形式。构造序列p1,p2,···,pm为第m种符合序列出现的概率大小。根据Shannon熵的思想，{x(i),i=1,2,3,···,n}的m种不同符号序列的排列熵将可以描述为

当Pl=1/m!时，PE(m)将得到最大值ln(m!)。嵌入维数m和延迟时间 τ对排列熵的计算有着一定的影响。在实际应用中，m一般取值3～7。这是由于当m取值较小时，则重构的向量中含有的状态将会很少。如果m取值较大，则重构时将会均匀化时间序列，这将使得序列中的细微变化无法得到体现，本文选取m=5。τ的选取对排列熵的影响很小，本文取τ=2。为了更加直观地反映信号的信息，通常对其进行归一化，即

式(5)中，PE的取值范围为 0≤PE≤1，PE值的大小可表示为时间序列{X(i),i=1,2,3,···,N}的复杂度和随机程度。当熵取值越大的时候，所表示的信息的无序度也将会越高，因而效用值就越大。该套理论很好地描述了概率系统的平均不确定度。

1.2 人工蜂群算法原理

人工蜂群算法是一种模仿自然界中的蜜蜂采蜜过程的算法。它的特点是可以在对所处理的问题不甚了解的情况下，仅仅利用蜂群对求解的问题展开不断的比较分析，然后得到全局最优解。在该算法中，蜜蜂由雇佣蜂、跟随蜂和侦查蜂而组成。上述3种类型的蜜蜂在搜索蜜源的不同阶段里完成各自的职责，并通过分享蜜源信息从而寻找到问题的最优解。在该算法中，最佳蜜源的位置对应最优解。同时，蜜源所含有的花蜜量对应于适应度值。设定第i个蜜源在N维空间中的位置是Vi=(Vi1,Vi2,···,ViN)，那么雇佣蜂和跟随蜂将根据式(6)来生成蜜源。

式中，k∈(1,2,···,L)，j∈(1,2,···,N)，k≠j；r为[−1,1]间的随机数；Sij为蜜源当前的位置；Skj为新蜜源的位置。

依据雇佣蜂提供的信息，跟随蜂按式(7)来计算被选择的概率。

依据是否大于0的原则，适应度函数被表示为

式(8)中，σi为第i个蜜源；f(σi)为第 σi处蜜源的适应度值，i∈{1,2,3,···,T}；T为蜜源的数量。通过对f(σi)进行比较，跟随蜂在邻近的蜜源中选取某个蜜源。

经过设定的最大limit次开采次数后，如果蜜源的质量仍旧无法得到改善，则雇佣蜂将转变为侦查蜂，并放弃目前的蜜源，转而用式(9)的方式产生一个新蜜源。

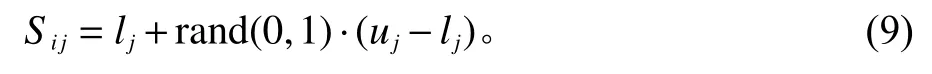
式中，rand(0,1)是[0,1]间的随机数；[lj,uj]是第j维变量的边界。

2 基于LMD排列熵和ABC-KELM的单向阀故障诊断模型

通过对原始信号进行LMD分解后，首先，采用LMD对不同故障下的单向阀振动信号展开分解，并获得若干个PF分量。由于这些PF分量中包含了一些和原始信号关联度较弱且无法很好地反映原信号特征的分量，为选取代表主要故障信息的PF分量，本文引入互相关准则来进行筛选。根据互相关准则的定义可知，相关系数可用作衡量两个信号间关联程度的评价指标，而且其取值越大表示相关度越高。通过利用该准则，可以更为准确地判断出各PF分量与原信号存在的内在关系。

求出各个PF分量的相关系数值后，以此为依据来进一步提取出排列熵作为待输入的特征向量。其计算方式为

其中，xi和分别是信号x的具体值与平均值；yi和分别是信号y的具体值与平均值。

1) 按照一定的采样频率采集单向阀振动信号，并获得不同故障样本数据；

2) 对不同故障状态下的单向阀信号作LMD分解，然后求出多个频率从高到低的PF分量和一个残量R；

3) 根据互相关准则计算出各PF分量的互相关系数，然后通过比较各PF分量的相关系数值，从中筛选得到互相关程度较高的PF分量；

4) 对筛选得到的PF分量分别求出对应的排列熵，并构建待输入的特征向量。

在传统的ELM中，隐层输出矩阵是通过随机赋值产生的。由于随机赋值的不确定性，每次建模分析的时候，所求出的矩阵都不相同。因而经过进一步计算得到的隐层输出权值也会不同，这直接影响了ELM模型的稳定性和泛化能力。为解决上述问题，Huang等[13]通过对比ELM与支持向量机的基本原理，将核函数的概念引入到ELM中，提出核极限学习机 (kernel based extreme learning machine,KELM)算法。由于径向基核函数不但有着结构简单、泛化性能优异的优势，而且所需优化的参数较少，本文选取该函数作为核函数。同时，待优化的参数为正则化参数 γ和核函数宽度 σ2。由于模仿了生物进化机制的群智能优化算法——人工蜂群算法在解决复杂优化问题上具有优异的全局优化能力，并在实际应用中取得良好的效果。所以本文引入ABC算法对KELM的参数进行优化，故障诊断模型建立的主要过程如下。

1) 对提取的特征向量数据进行归一化，并将KELM模型中的(γ,σ2)编码成为初始解；

2) 对ABC算法中的参数进行初始化，包括蜂群数目、最大迭代次数、终止循环次数等；

3) 生成一定数量的蜜源，并计算其对应的适应度值；

4) 在蜜源附近，按照式(6)寻找新的蜜源，并计算其适应度值。经过比较，如果该蜜源优于原来的蜜源，那么将采取用新蜜源来替换原来的蜜源的操作；

5) 按照式(7)计算蜜源选择的概率，然后使用轮盘赌的方式计算解的收益率，并从中选取新的蜜源；

6) 当经过limit次循环后，则说明该蜜源无法被继续优化，侦查蜂将会随机产生一个新的蜜源来进行替换；

7) 当算法的迭代次数大于所设定的最大迭代次数时，优化结束，然后输出最优解，否则返回步骤3)继续寻优；

8) 根据得到的最优参数(γ,σ2)构建故障诊断模型。

该方法的流程如图1所示。

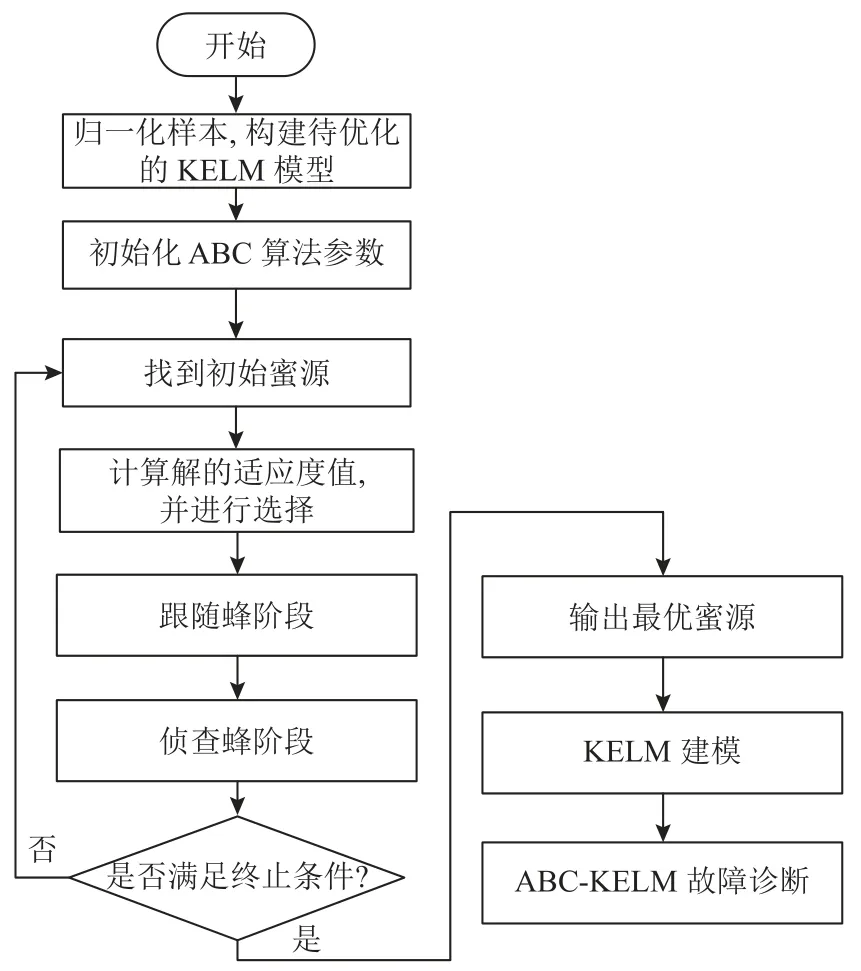
图1 基于ABC-KELM的单向阀故障诊断流程Figure 1 One way valve fault diagnosis process based on ABC-KELM

3 实验分析

为验证本文所提出方法的有效性，采用中国西部某矿浆输送管线的高压隔膜泵单向阀数据采集系统所采集到的实际现场数据作为故障检测的依据，并进行分析。隔膜泵的工作原理示意图如图2所示，电动机通过传动系统带动三拐曲轴、连杆、十字头，带动活塞做往复运动。通过这一操作，进口单向阀和出口单向阀保持着不断的开启和闭合的工作状态，并使得矿浆经历着不断的吸入和排出的过程。所采集到的振动信号包括正常运行、粗颗粒卡阀和磨损击穿3种状态。

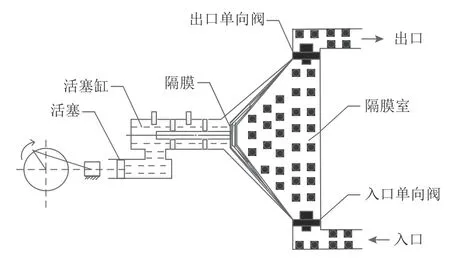
图2 隔膜泵工作原理图Figure 2 Working principle of diaphragm pump

采用LMD分解法对基于不同故障状态下的单向阀振动信号进行分解，结果如图3(a)、图4(a)和图5(a)所示。从中可以看出，信号经过分解后，可得到4个PF分量和1个残余分量。所以，单向阀处于正常运行、磨损击穿状态和粗颗粒卡阀状态下的故障信息集中在前4个PF分量中。为突出本文所提方法的优越性，同时采用传统的EMD算法对故障信号进行分解，所得到的结果如图3(b)、图4(b)和图5(b)所示。从中可以看出，经过EMD分解得到更多的信号分量，且上述信号分量存在一定程度的模态混叠，同时产生很多虚假分量。为选取相关程度较高的信号分量，接下来将计算各PF分量、IMF分量和原始信号的互相关系数，结果如表1所示。

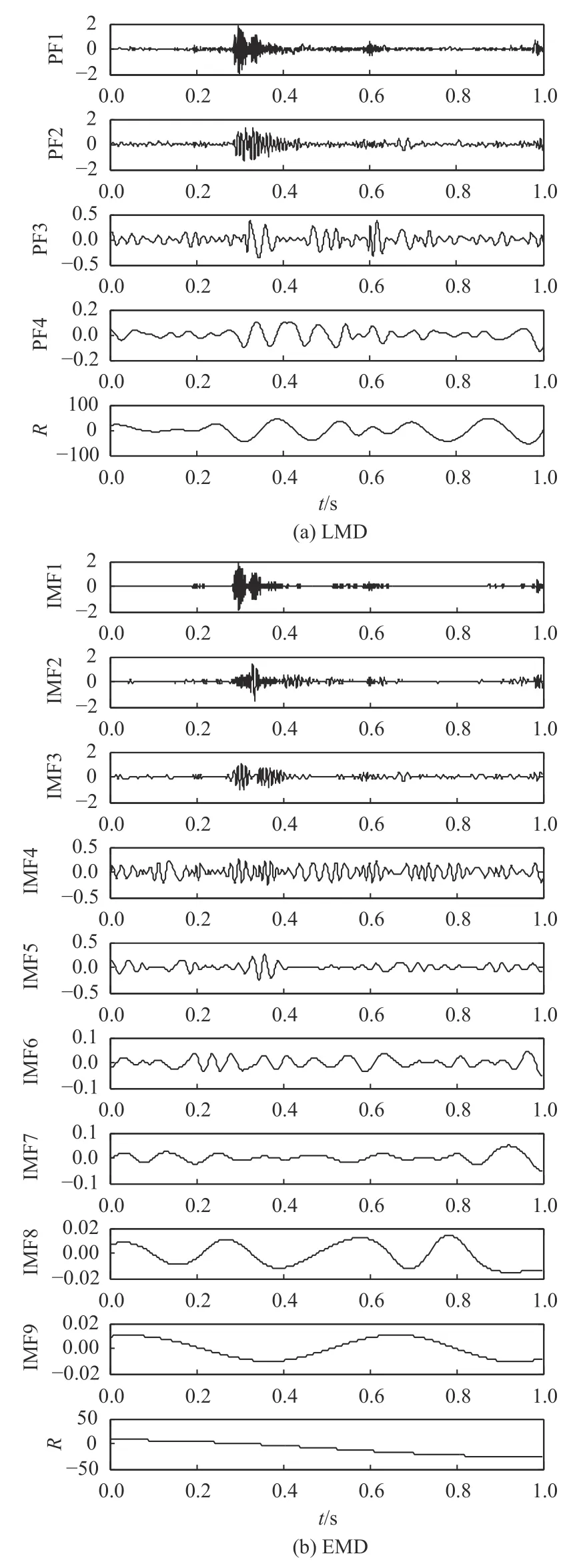
图3 单向阀正常运行状态下LMD和EMD方法分解结果Figure 3 Decomposition results of LMD and EMD methods under normal operation of check valve

图4 单向阀磨损击穿状态下LMD和EMD方法分解结果Figure 4 Decomposition results of LMD and EMD methods under wear and breakdown state of check valve

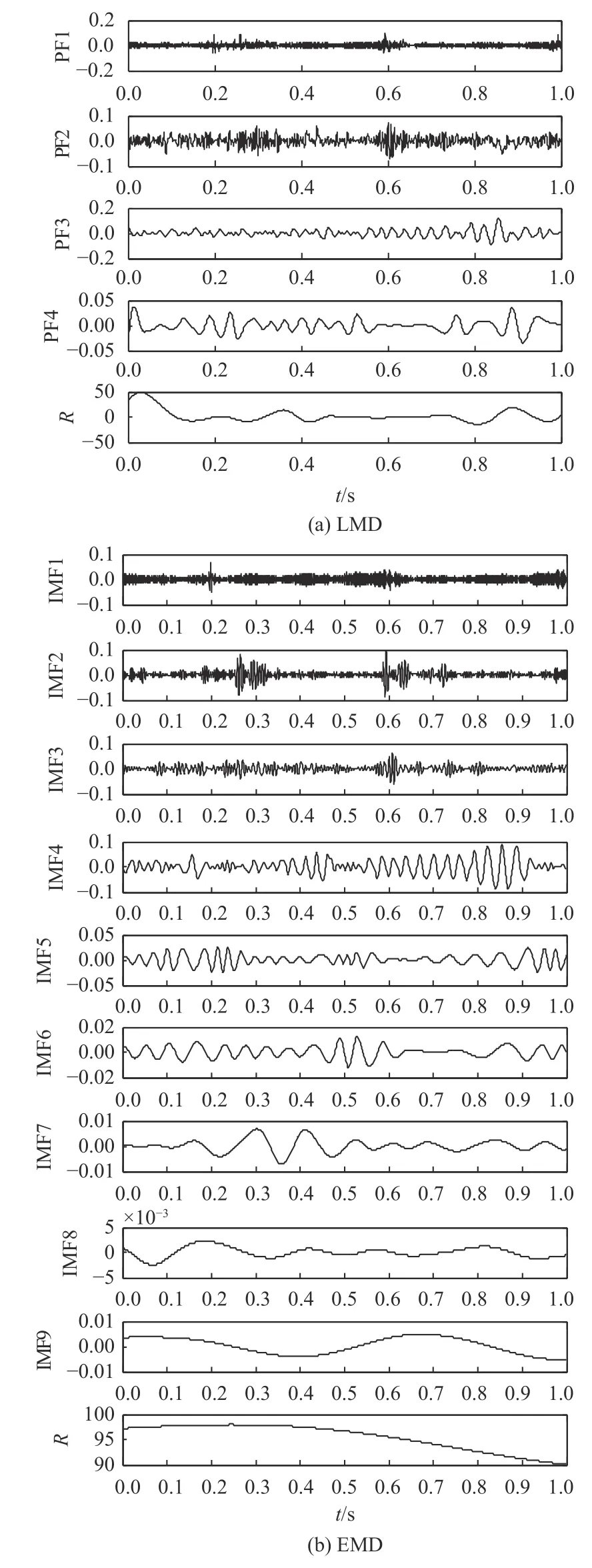
图5 单向阀粗颗粒卡阀状态下LMD和EMD方法分解结果Figure 5 Decomposition results of LMD and EMD methods under coarse particles stuck of check valve

表1 基于LMD分解的PF分量相关性分析Table 1 Correlation analysis of PF components based on LMD decomposition

从表1可知，经过LMD分解后，所得到的PF分量中与原信号相关程度较高地均集中于前3个PF分量，且互相关系数值大于0.3，说明上述分量信号与原信号的相关度较高。而剩余的分量与原始信号的互相关程度较弱。因此，本文将选取每种故障状态下的前3个PF分量进行排列熵特征的提取。与此同时，基于EMD分解法得到的IMF分量与和原始信号的互相关分析如表2所示。从表2中可知，经过EMD分解后，单向阀处于正常运行状态下的信号分解得到的前3个IMF分量与原信号的相关程度较高，且互相关系数值大于0.3。同时，单向阀处于磨损击穿和粗颗粒卡阀的信号分解得到的IMF2、IMF3和IMF4分量与原信号的相关程度较高，且互相关系数值大于0.3。因此，选取正常运行状态下信号分解得到的前3个IMF分量和磨损击穿、粗颗粒卡阀状态下信号分解得到的IMF2、IMF3和IMF4分量进行排列熵特征的提取。在本文实验中，所提取得到的3种故障状态的特征数据分别有60组、30组和30组。实验选取正常运行状态下的前40组数据作为训练样本，粗颗粒卡阀、磨损击穿状态下的前17组数据作为训练样本，并将剩余的数据作为测试样本。基于LMD分解法得到的部分不同故障状态下提取得到的排列熵值如表3所示，基于EMD分解法得到的部分不同故障状态下提取得到的排列熵值如表4所示。

表2 基于EMD分解的IMF分量相关性分析Table 2 Correlation analysis of IMF components based on EMD decomposition

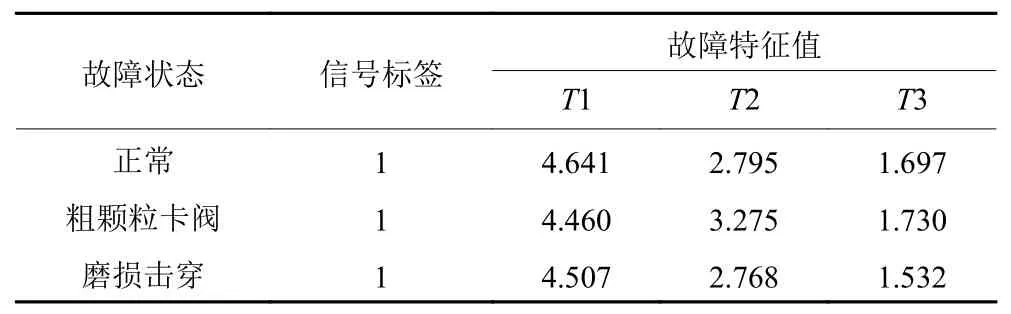
表3 基于LMD分解的单向阀处于不同状态下的部分故障特征数据Table 3 Partial fault characteristic data of check valve in different states based on LMD decomposition

表4 基于EMD分解的单向阀处于不同状态下的部分故障特征数据Table 4 Partial fault characteristic data of check valve in different states based on EMD decomposition

为进行识别效果的比较，分别将基于LMD分解法和EMD分解法提取得到的排列熵特征输入至KELM模型中进行建模分析，模型的识别结果如表5所示。由表5可知，在基于LMD分解法建模的识别中，单向阀正常运行、磨损击穿状态和粗颗粒卡阀状态被正确识别的个数分别为20、13和9，识别准确率达到91.3%。在基于EMD分解法建模的识别中，单向阀正常运行、磨损击穿状态和粗颗粒卡阀状态被正确识别的个数分别为20、13和5，识别准确率仅为82.61%。同时，在粗颗粒卡阀故障的识别中，误诊率相对较高。由于基于LMD的方法在迭代次数和抑制端点效应上的表现要优于EMD方法，且减小了EMD分解带来的模态混叠程度，使得所提取出的特征更充分地反映原信号的运行状态，因而识别准确率相对更高。

表5 基于不同信号分解法的模型识别结果对比Table 5 Comparison of model recognition results based on different signal decomposition methods

接下来，采用基于LMD分解法得到的单向阀不同故障状态下的特征集，并通过本文所提出的ABC优化KELM的方式进行故障诊断效果的测试实验。在本实验中，初始化参数设置如下。蜂群规模为40，雇佣蜂和跟随蜂的数目都为20，最大迭代次数为100次，规定终止循环次数为30次。正则化参数和核函数宽度的参数搜索范围设置为 γ∈[0.01,800]、σ2∈[0.01,5]。经改进的ABC算法寻优后，得到的最优参数(γ,σ2)为(58.128，0.169 7)。为了对本文提出的ABC参数优化KELM模型和采用常规方法的识别效果进行比较，本文同时使用KELM和ELM模型来对单向阀的故障进行识别测试。图6为利用ABC-KELM模型、KELM模型和SVM模型得到的识别结果。将单向阀正常运行状态、粗颗粒卡阀、磨损击穿3种状态的数据标签分别记为1、2和3。表6对上述3种模型的识别效果进行具体的比较分析。

由图6和表6中的识别结果可知，采用ABC-KELM模型的识别准确率为95.65%，且仅有2个样本被错误识别。而采用传统的KELM、ELM模型的识别结果仅为91.3%。其进一步验证了通过ABC算法能够取得全局最优解。同时，由于受到数据样本不均衡带来的影响，增大了占比小的样本被错分的可能性。例如，在基于KELM和ELM模型得到的结果中，粗颗粒卡阀被误诊的概率均达到30%，基于KELM模型的识别效果相比其他模型则要好很多，其不但取得了最优的总体识别效果，而且还降低了对小样本的堵塞故障误诊的概率。

图6 基于ABC-KELM、KELM和SVM的识别结果Figure 6 Recognition results based on ABC-KELM、KELM and SVM

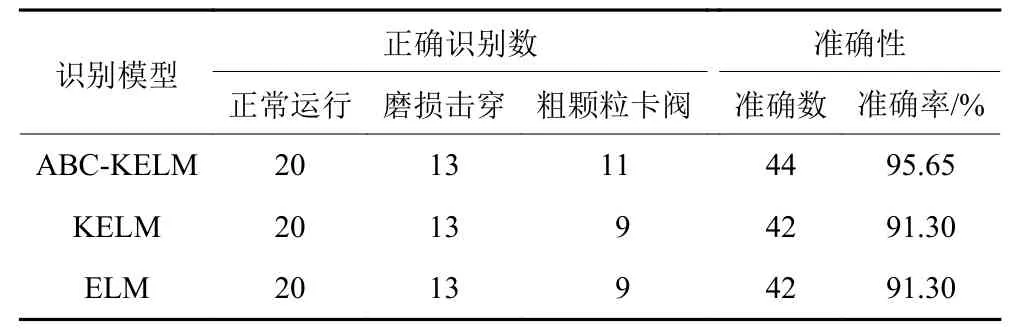
表6 不同模型的识别结果对比Table 6 Comparison of recognition results of different models

4 结论

本文针对高压隔膜泵单向阀故障振动信号的非平稳特性，提出LMD和ABC-KELM相结合的方法对单向阀的故障状态进行诊断分析，并得出如下结论。

1) 为提取单向阀的非平稳信号特征，本文通过LMD方法将所采集到单向阀的3种状态下的振动信号分解成若干个PF分量，且得到的PF分量较好地表征了原信号不同的局部特征信息。实验分析，验证了基于LMD排列熵的方法在识别精度上要优于EMD排列熵的方法。同时，也证明了利用排列熵对单向阀的运行状况进行度量能够较好地表征单向阀故障特征和不同频带下信号的复杂性。

2) 利用ABC优化KELM模型中的惩罚因子和核函数，避免参数选取的盲目性对模型识别的不利影响，并取得了较好的效果。同时，和原有KELM、ELM模型得到的结果相比，在识别精度上表现出良好的优势。该方法为高压隔膜泵的单向阀故障诊断提供了一种可行的途径。