基于GRA-PCA-BP神经网络模型的单沟泥石流危险性预测
刘育林,周爱红,b,袁 颖,b
河北地质大学 a.勘查技术与工程学院、b. 河北省高校生态环境地质应用技术研发中心,河北 石家庄 050031
1 引言
泥石流作为山区常见的地质灾害,广泛分布于全国各地,每年都会对当地居民造成巨大的财产损失。因此,合理有效地对泥石流危险性进行评价对于山区的防灾减灾工作具有重大意义。
目前,应用于泥石流危险性评价的方法有很多,例如张云峰[1]利用层次分析法确定评价指标的权重值,并结合可拓理论对泥石流危险性进行评价;田运涛[2]将粗糙集与逐步回归理论相结合对评价指标进行了精确的筛选,采用组合赋权法为筛选出的评价指标进行赋值,利用模糊综合评价法对泥石流危险性进行评价;刘炜[3]采用尖点突变理论对评价指标进行筛选和排序,建立多层突变理论模型对泥石流危险性进行评价;尹超[4]利用云模型改进的层次分析算法计算评价指标的权重,并基于Arcgis对泥石流进行危险性评价;周仲礼[5]采用粗糙集理论对评价指标进行筛选,结合决策树理论构建泥石流危险性预测模型,对泥石流危险性进行评价;吕擎峰[6]采用灰色关联度法确定评价指标的权重,基于可拓理论通过定性和类比的方法对泥石流危险性进行评价;王常明[7]利用模糊c均值聚类的方法对评价指标进行了分类,并结合SVM模型对泥石流危险性进行评价。
对上述各种泥石流危险性评价方法进行分析,发现在泥石流危险性评价过程中虽然评价方法多种多样,但是各种方法都采用了不同的手段对评价指标进行了一定的处理。考虑到影响泥石流危险性的评价指标众多,这些评价指标间往往具有相关性、模糊性和不确定性,并且许多评价指标预处理手段确定的指标在地质学角度难以得到合理的解释。因此,为实现泥石流危险性的有效预测,本文利用灰色关联度模型确定各评价指标与泥石流危险性的关联度和评价指标权重系数,剔除关联度和权重系数较小的评价指标,建立对泥石流危险性影响较大的关键指标集,进而分析同一指标在不同危险性的样本中的平均值,基于统计学理论对选取的评价指标进行分析,进而从全新的角度对所选指标的合理性进行了解释;然后通过主成分分析提取关键指标集中评价指标的特征信息构造出线性无关的主成分,剔除关键指标集中包含的冗余信息,并结合BP神经网络强大的非线性映射能力和容错能力,建立基于GRA-PCA-BP神经网络的泥石流危险性预测模型,将预测结果与BP神经网络模型、GRA-BP神经网络和PCA-BP神经网络模型的预测结果进行对比,以期为泥石流危险性评价提供一种新的思路。
2 理论简介
2.1 灰色关联度
灰色关联度理论作为灰色系统理论的重要组成部分。目前被广泛应用于计算评价指标的权重,它通过关联度的概念描述系统中两个事物的相关程度,两个事物的相关程度越大,相应序列的变化趋势也就越相近,而这种变化趋势主要通过这两个事物相应序列曲线的相似度来体现,称其为灰色关联度[8-10]。因此,为了对影响泥石流危险性的评价指标进行约简,以泥石流危险性作为参考序列,各评价指标为比较序列,根据泥石流危险性序列与评价指标序列间的曲线相似度,确定各评价指标与泥石流危险性的关联度及评价指标权重系数,剔除对泥石流危险性影响较小的评价指标。
2.2 主成分分析
主成分分析是基于统计学理论的一种常用的数据处理手段,该理论采用正交变换的方法将原来评价指标中包含的信息转化为一组新的线性无关的主成分。主成分分析剔除了评价指标内部的冗余信息,并采用累计贡献率的方法确定主成分的个数,尽可能多的保留评价指标中的有效信息[11-13]。因此,为降低建立泥石流危险性预测模型的难度、提高模型的预测精度,采取主成分分析的方法提取评价指标中的特征信息,剔除评价指标中包含的冗余信息。
2.3 BP神经网络
BP神经网络是一种误差逆向传播的多层前馈神经网络,是目前应用最广泛的神经网络之一。BP神经网络作为一种智能信息处理手段,它不需要事先确定输入向量与输出向量之间繁杂的映射关系,而是通过自身的训练不断的调整权值和阈值使模型预测值接近期望值。当神经网络模型充分学习了这种复杂的非线性映射关系后,就能够处理具有相似信息的样本,达到有效预测的目的[15-18]。因此,为实现泥石流危险性的有效预测,将影响泥石流危险性的评价指标作为输入,泥石流危险性作为输出,结合神经网络强大的非线性映射能力和泛化能力建立BP神经网络模型,将其应用到泥石流危险性评价当中去。
3 评价指标的处理
3.1 评价指标的选取
本文以《泥石流危险性评价》[19]中云南省的37条泥石流样本为原始样本数据集,根据前人的研究经验选取泥石流一次最大冲出量(S1)、泥石流发生频率(S2)、流域面积(S3)、主沟长度(S4)、流域最大相对高差(S5)、流域切割密度(S6)、植被覆盖密度(S7)、松散固体物质储量(S8)、24h最大降雨量(S9)和流域人口密度(S10)共10个影响因素作为泥石流危险性评价的评价指标,并选择28组泥石流样本作为BP神经网络模型的训练样本(表1),9组泥石流样本作为BP神经网络模型的预测样本(表2)。危险性一栏中的1、2、3分别代表泥石流从低到高的危险性等级。

表1 泥石流危险性评价训练样本Table 1 Training sample of debris flow risk assessment
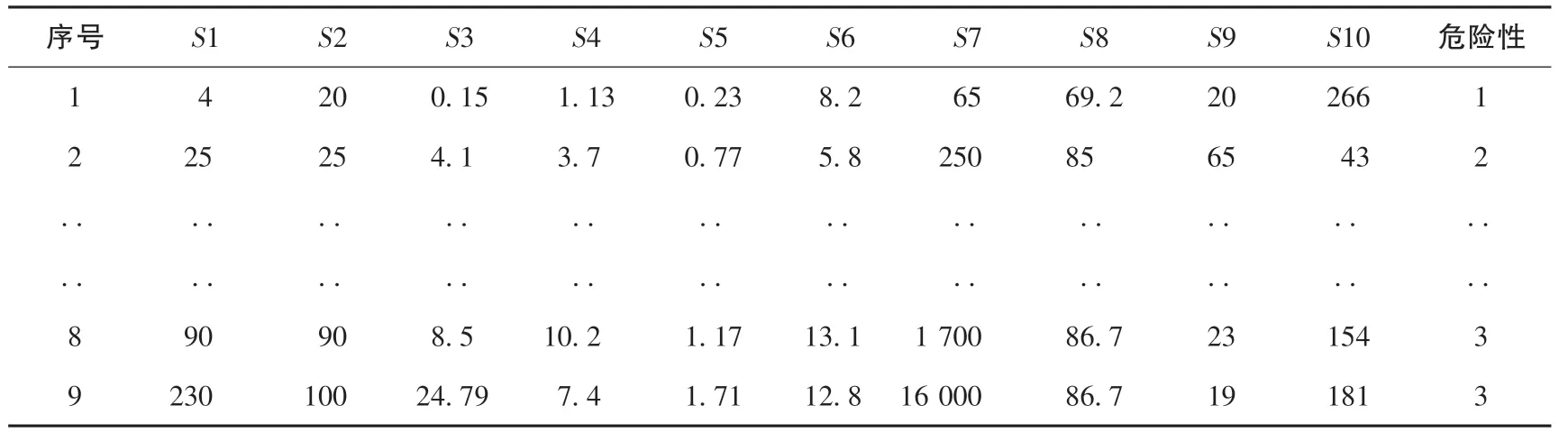
表2 泥石流危险性评价预测样本Table 2 Prediction sample of debris flow risk assessment
3.2 基于GRA模型的信息分析
泥石流危险性评价涉及很多的评价指标,选取的评价指标体系不同,泥石流危险性评价模型的预测效果也会有较大差异。因此,为了筛选出与泥石流危险性相关程度较高的评价指标,本文采用灰色关联度对原始数据(表1、表2)中泥石流危险性与评价指标的相关程度进行分析,选取泥石流的危险性作为参考序列记x0(k)= {x0(1),x0(2),…,x0(37)},评价指标构成比较数列,分别记为xi(k) ={xi(1),xi(2),…,xi(37)},式中i=1,2,…,10代表S1到S10这10个评价指标,采用公式(1)计算原始数据中泥石流危险性与各评价指标的关联系数,得到关联系数矩阵(表3),接着利用式(2)与(3)分别计算出评价指标与泥石流危险性的关联度和评价指标的权重系数,并将评价指标分别按关联度和权重系数的大小排列起来如图 1和图2所示,以此反映评价指标与泥石流危险性相关程度的大小。

表3 关联系数矩阵Table 3 Correlation coefficient matrix

由图 1和图 2不难看出,各评价指标与泥石流危险性的相关程度有较大差异。为了能够有效地剔除与泥石流危险性相关程度较小的评价指标,又不损失样本中过多的数据信息,通过阅读大量文献,根据前人的经验选取关联度≥0.8并且权重系数≥0.10的流域最大相对高差(S5)、主沟长度(S4)、流域切割密度(S6)、流域面积(S3)、24h最大降雨量(S9)、泥石流发生频率(S2)和泥石流一次最大冲出量(S1)共7个评价指标作为关键指标集。该集合中的评价指标与泥石流危险性的相关程度较大,在泥石流危险性评价中起着重要的作用,若将其中的部分评价指标剔除会显著降低样本中所包含信息对泥石流危险性的评价能力。松散固体物质储量(S8)、流域人口密度(S10)和植被覆盖密度(S7)这3个评价指标与泥石流危险性相关程度较小,将它们剔除后关键指标集中的评价指标仍然能够有效地对泥石流危险性进行评价。但是从地质灾害学的角度分析不完全合理:松散固体物质储量(S8)作为泥石流形成的三大因素之一;植被覆盖密度(S7)可直接的影响到坡体的结构、强度、含水量等物理力学性能,并且很大程度上影响松散固体物质(S8)的产生;流域人口密度(S10)与泥石流关系极为密切。
综上所述,所得评价指标体系合理性仍有待探索分析。
为判断上述评价指标简约的合理性,对不同危险性下各评价指标的平均值分析。不同危险性下各指标归一化平均值见表4。

表4 不同危险性下各指标的平均值和方差Table 4 Mean and variance of each index under different hazards
由上表可以看出,随着泥石流危险性增加,S7 、S8分别呈递增、递减趋势,而S10在中危险时最大,低危险时最小。由主观分析可知,泥石流危险性随着松散固体物质储量(S8)和流域人口密度(S10)增大而增大;随植被覆盖密度(S7)增大而减小,与表4所呈现的规律不符。由此可知,选择剔除松散固体物质储量(S8)、流域人口密度(S10)和植被覆盖密度(S7)这3个评价指标相对合理。
上述分析在一定程度上对评价指标的选取做出了解释,但仍未能完全反映影响因素与泥石流危险性之间的关系。这一方面是由于样本实例仅37组,数量较少,难以真实全面地反映影响因素与泥石流危险性之间复杂的物理力学关系;另一方面是由于GRA归根结底是一种数学工具,它计算分析的是各指标和结果的量化数值,而不是影响因素本身,所以会忽略指标本身所表征的意义。综上所述,虽然GRA在一定程度上有其局限性,但是其因素约简的结果仍是真实可靠的。
虽然上述方法对原始指标体系中的冗余指标进行了剔除,但是,经GRA模型处理后得到的评价指标间可能包含了大量的重叠信息,因此,仍需要对关键指标集中的评价指标进行进一步的处理。
3.3 关键指标集的主成分分析
由于灰色关联度仅完成了评价指标的约简,对于评价指标间存在的重叠信息并未进行有效的处理,因此对关键指标集合中的评价指标进行主成分分析。首先,将关键指标集中的数据调整为与公式(4)相同的形式,采用max-min标准化方法对关键指标集中的评价指标进行归一化处理消除不同量纲的影响,并通过式(5)计算出相关系数矩阵(表5)反映评价指标间的相关关系。然后,由式(6)和(7)计算各主成分的贡献率和累计贡献率并确定主成分的个数,结果如表6所示。接着根据最大方差一次旋转法得到因子载荷矩阵(表7)反映主成分与评价指标间的相关关系。最后根据(表8)中的得分系数采用式(8)计算各主成分的值。在此过程中清楚地阐述评价指标间的关系以及评价指标与主成分间的关系。
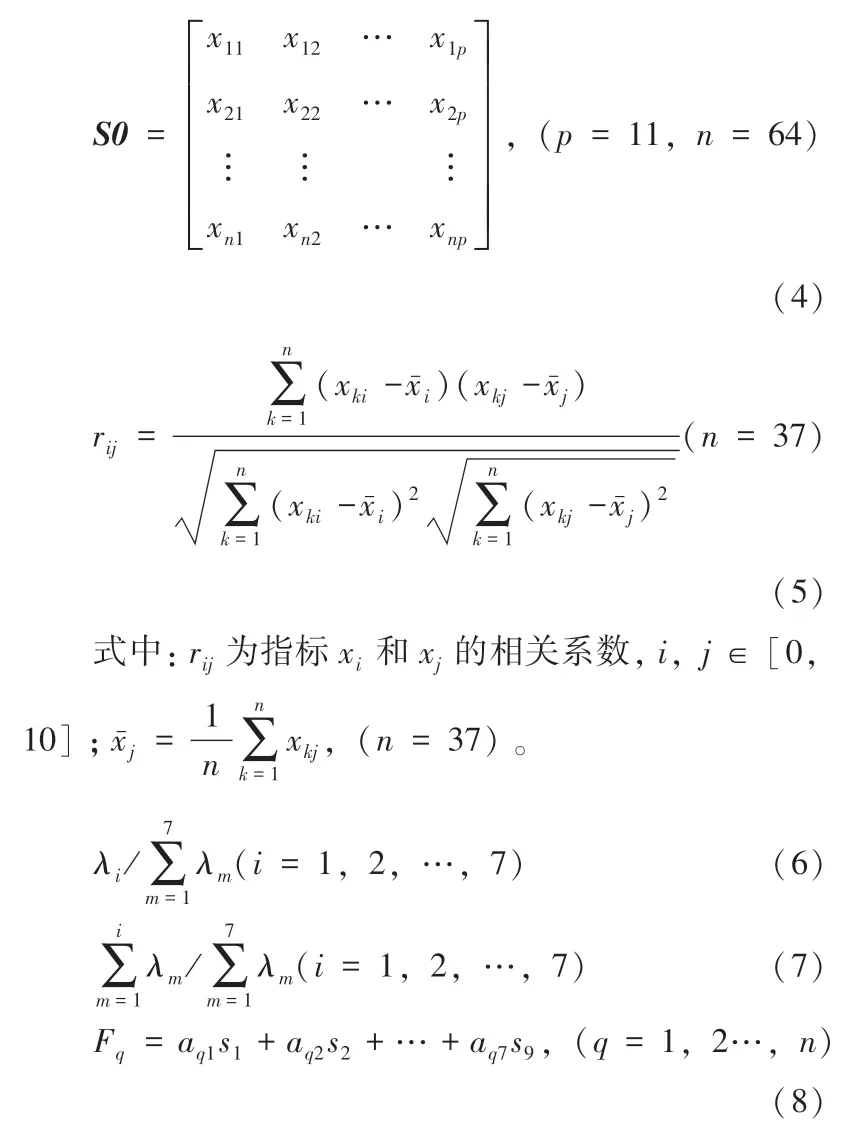

表5 相关系数矩阵Table 5 Correlation coefficient matrix
式中:Fq为主成分;aq1…aq7为得分系数;s1…s9为关键指标集中的7个评价指标。
由表5中评价指标的两两关系不难看出,S1与S2、S3与S4和S4与S5等评价指标间的相关系数较大,表明这些指标间存在着复杂的相关关系,包含了大量的重叠信息。因此,有必要对这些相关性较大的评价指标进行主成分分析,提取各指标所包含的特征信息形成一组线性无关的主成分,通过对评价指标进行降维,降低后续BP神经网络模型建立的难度。
由表6可知,主成分F1的特征值为4.13,贡献率为58.99%;主成分F2的特征值为1.30,贡献率为18.52%;主成分F3的特征值为0.69,贡献率为9.81%;主成分F4、F5、F6和F7的特征值相对较小且其解释方差的贡献率也相对较低。因此,本文确定采用前3个主成分代替关键指标集中的7个评价指标,累计贡献率为87.32%>85%,并认为提取出的主成分能够有效反映关键指标集中所包含的有效信息。

表6 主成分特征值及贡献率Table 6 Characteristic value and contribution rate of main components
由表7中各评价指标在主成分上的载荷值不难看出主沟长度(S4)、流域面积(S3)和流域最大相对高差(S5)在主成分F1上载荷值较大;泥石流发生频率(S2)和泥石流一次最大冲出量(S1)在主成分F2上载荷值较大;流域切割密度(S6)和24h最大降雨量(S9)在主成分F3上载荷值较大。从该载荷值分布可知主成分F1反映了地形地貌条件对泥石流危险性的影响;主成分F2反映了物源条件对泥石流危险性的影响;主成分F3反映了构造和降雨等条件对泥石流危险性的影响。

表7 因子载荷矩阵Table 7 Factor load matrix
将表8中评价指标的得分系数与关键指标采用公式(8)进行线性组合,得到主成分F1、F2和F3,将这3个线性无关的主成分代替原来7个关键指标作为输入变量建立BP神经网络模型,降低输入变量的维数,以求提高建模的效率和预测结果的精度。


表8 评价指标得分系数矩阵Table 8 Score coefficient matrix of evaluation index
4 基于GRA-PCA-BP神经网络的泥石流危险性预测
4.1 BP神经网络结构的建立
因经灰色关联度和主成分分析处理最终得到3个主成分F1、F2和F3,将这3个主成分作为神经网络模型的输入变量,泥石流危险性作为神经网络模型的输出变量。故神经网络的输入节点数设为3,输出节点数设为1。由经验公式输出节点数;ni:输入节点数;a:1-10的常数)并结合试凑法确定隐含层最优节点数为8,最终BP神经网络泥石流危险性预测模型的网络结构为(3,8,1)型如图3所示。

图3 BP神经网络模型结构图Fig.3 Structure of BP neural network model
4.2 BP神经网络的训练
本文以表1中经灰色关联度和主成分分析处理后的28组样本作为BP神经网络模型的训练样本,在BP神经网络中引入L-M优化算法对网络进行训练,以求快速准确地确定权值和阈值。经多次试验,L-M算法最优参数设定如下:网络训练函数为收敛速率较快的trainlm函数;最大迭代次数为10 000次;精度设置为0.01。最终经176次迭代网络收敛,模型精度达到上述要求,样本训练结果见图4。由图可知BP神经网络预测的泥石流危险性与实际情况基本吻合,这表明神经网络经训练确定的权值和阈值是满足预测要求的。

图4 BP神经网络训练结果Fig.4 Training results of BP neural network
4.3 GRA-PCA-BP神经网络预测效果与分析
采用4.2节建立的GRA-PCA-BP神经网络模型对表8中9组泥石流样本的危险性进行预测,并根据泥石流实际危险性将预测结果(图5)与BP神经网络模型(图6)、GRA-BP神经网络模型(图7)和PCA-BP神经网络模型的预测结果(图8)进行对比,如表9所示。

表9 神经网络模型预测结果Table 9 Prediction results of neural network model
由图6和图7可知,GRA-BP神经网络模型预测结果的准确率与BP神经网络模型相比并没有明显的改善,表明仅仅通过约简剔除与预测结果相关程度较低的评价指标不能有效的提高模型的预测精度;由图6和图8可知,PCA-BP神经网络模型预测结果的准确率与BP神经网络模型相比有一定的提高,表明采取主成分提取评价指标特征信息的方法能够提高模型的预测精度;而通过对比图5、图7和图8发现,GRA-PCA-BP神经网络模型使灰色关联度模型评价指标约简的效果以及主成分分析提取特征信息的能力得到了充分体现,模型预测结果的准确率得到了显著的提高。
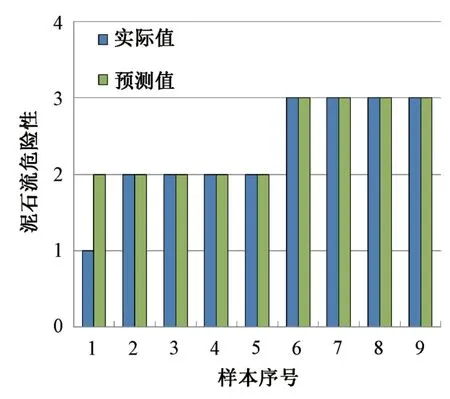
图5 GRA-PCA-BP神经网络模型预测结果Fig.5 Prediction results of GRA-PCA-BP neural network model

图6 BP神经网络预测结果Fig.6 Prediction results of BP neural network

图7 GRA-BP神经网络模型预测结果Fig.7 Prediction results of GRA-BP neural network model

图8 PCA-BP神经网络模型预测结果Fig.8 Prediction results of PCA-BP Neural Network Model
由表9不难看出,GRA-PCA-BP神经网络模型的预测结果准确率为88.90%明显高于其他3种神经网络模型,表明GRA-PCA-BP神经网络模型较其他3种神经网络模型能够在泥石流危险性评价中有更广泛的应用。由图5可知,GRA-PCA-BP神经网络模型的泥石流危险性预测值与实际值基本吻合,能够实现复杂的非线性映射功能,非常适用于影响因素众多、内部机制复杂的泥石流危险性评价问题。
5 结论
(1)经GRA确定的指标在地质学角度难以得到合理的解释,本文通过分析同一指标在不同危险性的样本中的平均值,基于统计学理论对选取的评价指标进行解释,其结果体现出一定的规律性。不仅从评价指标间及评价指标与结果间对评价指标进行处理,还从全新的角度对所选指标的合理性进行了解释,最终合理准确的确定了单沟泥石流危险性判定的关键指标。
(2)泥石流危险性评价的影响因素众多,本文基于GRA-PCA-BP神经网络模型的预测方法,通过引入灰色关联度模型对评价指标进行约简,确定了与危险性相关程度较高的7个评价指标,降低了BP神经网络输入层的维数;采用主成分对关键指标进行处理,消除了关键指标间重叠信息的影响。GRA-PCA-BP神经网络模型方法不仅降低了建立模型的难度,提高了泥石流危险性预测的精度,还为泥石流危险性预测提供了一个更加实用、准确的手段。

