变载荷四旋翼无人机的自适应模糊自抗扰控制*

徐雪松, 吴仪政, 倪 赟

(华东交通大学 电气与自动化工程学院，江西 南昌 330013)

0 引 言

随着微机电系统(micro-electro-mechanical system，MEMS)在科技领域的发展，无人机(unmanned aerial vehicle,UAV)的应用范围也变得更广。无人机可代替人工去完成一些高风险、高强度的工作，例如军事任务、喷洒农药、配送快递、电路巡检等[1]。由于实际无人机飞行易受负载质量的变化以及周围未知环境的影响，使得无人机的载荷系统发生突变，导致无人机掉高或姿态失衡[2]，从而无法完成复杂的高空飞行任务。因此，考虑建立一个变载荷四旋翼无人机模型，并设计一个抗负载扰动能力强的飞行控制系统。

目前，国内外学者对四旋翼无人机抗扰动稳定飞行控制的方法有滑模控制、反步法控制、自适应控制、串级比例—积分—微分(proportion-integration-differentiation，PID)控制等[3～5]。采用串级PID控制应用于无人机系统的稳定控制，对角度、角速度的PID控制参数进行非线性化模糊整定[6],要求控制参数跟随系统的非线性变化自适应修正。但循环边界限制只在规定载荷范围内起作用，应对变载荷系统的自适应能力较差。进一步提出L1自适应块控反步控制方法，对外回路设计了块控反步控制器，对内回路引入L1自适应控制可补偿外部扰动及内部参数偏差[7]，但控制效果过于依赖数学模型精度，易受不确定性外界扰动影响。随后设计了自抗扰控制器(active disturbance rejection controller,ADRC)[8]，应用扩张状态观测器实现状态解耦和扰动估计解决了系统模型精度易受外界干扰的问题[9,10]。由于实际变载荷无人机飞行控制系统存在非线性时变的外界负载干扰等影响，使得自抗扰控制器的扰动估计补偿易出现较大误差，且自抗扰控制器存在调节参数过多难以整定的缺陷。

本文采用基于自适应变载荷补偿的模糊自抗扰控制器(adaptive fuzzy active disturbance rejection controller，AFADRC)应用于变载荷四旋翼无人机。首先，自适应控制可辨识负载系统的变化并能快速准确跟踪估计出负载变化量，从而可根据负载动态变化修正自抗扰控制器的外部扰动补偿系数，增强对非线性时变无人机系统抵抗负载扰动的鲁棒性和稳定性。其次，将模糊控制应用于自抗扰控制器中通过制定合理的模糊推理规则对控制参数进行在线自整定调节，能有效提升系统响应速度，更符合工程自动化应用需求。

1 变负载四旋翼无人机系统模型

携负载四旋翼无人机是固联十字交叉[11]。建立机体—地理坐标系如图1所示。

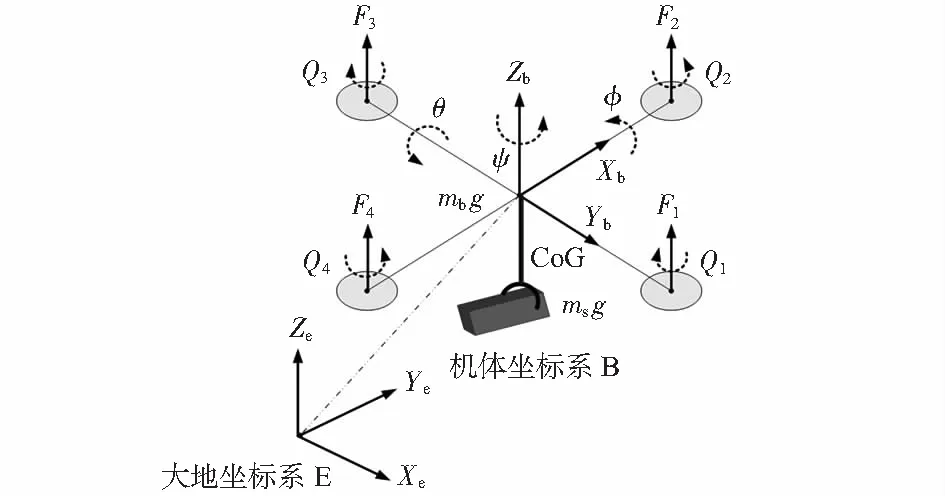
图1 携负载四旋翼无人机的机体—地理坐标系

根据牛顿—欧拉动力学方程和刚体运动定理[12]，建立变负载四旋翼无人机模型的三轴合力平衡方程和三轴合力矩平衡方程如下

(1)

(2)

式中Γ为无人机位置，ω为无人机角速度，F为作用于无人机上合外力；τ为机体坐标系下合外总力矩；机体总质量为m包括机身质量mb和负载质量ms；I为机体坐标系下的转动惯量。

无人机携负载的质心位置表达式为

(3)

式中rs为负载质心相对机体坐标系偏移量。

在地理坐标系下，升力总是沿z轴正方向，可得总升力Ft表达式为

(4)

式中Rb-e为坐标系旋转矩阵，b为旋翼的升力系数，Ω为旋翼的转速[13]。

机体旋翼产生的力矩Mp和作用于复合系统重力产生的力矩Fp可表示为

Mp=[U2U3U4]T

(5)

Fp=-(rG×Rb-e[0 0mg]T)

(6)

因此，系统合力矩τ以及合力F又可表示为

(7)

F=Ft-Fg

(8)

式中l为四旋翼无人机中心到旋翼中心的距离，d为旋翼的扭矩力系数，Fg为地理坐标系下重力矢量[14]。

整理式(1)、式(2)与式(7)、式(8)可得不确定变载荷四旋翼无人机6自由度动力学方程如下

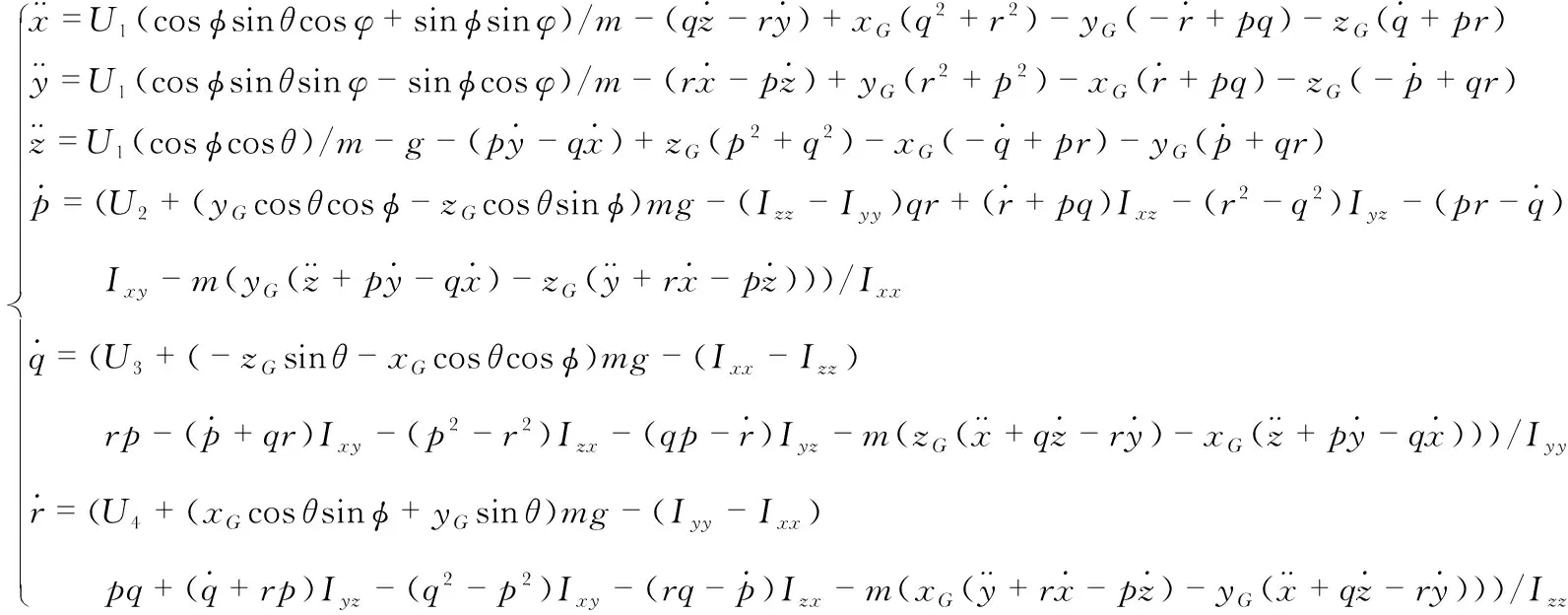
(9)

2 控制系统设计

为提高无人机控制系统对不确定扰动进行实时精准的估计和补偿。本文对自抗扰控制器进行改进，对变负载系统进行自适应跟踪估计，再由负载估计值调节扰动补偿系数，并在非线性状态误差反馈(nonlinear state error feedback,NLSEF)中引入模糊控制器实现参数快速自整定调节，控制系统结构框图如图2所示。

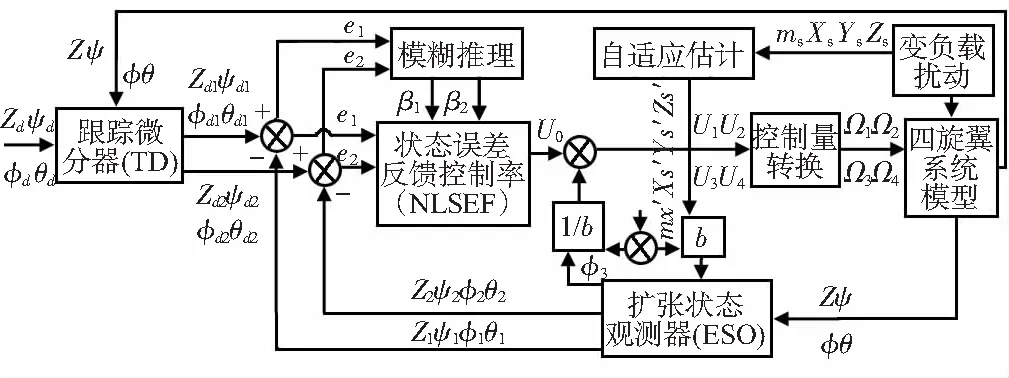
图2 控制系统结构框图

2.1 补偿系数自适应控制器设计

无人机携带负载存在的不确定性会导致自抗扰控制中扰动补偿系数出现较大偏差难以精准补偿。为此设计自适应控制器使得估计负载量与预期负载量之间误差趋近于零，再由估计负载量求得准确补偿系数，从而提高扰动补偿精度。

将无人机控制对象的变载荷子系统表示为

(10)

式中a为被估对象的未知参数，且可任意变化。u为待设计的控制器输入函数。设计控制器具体步骤如图3。

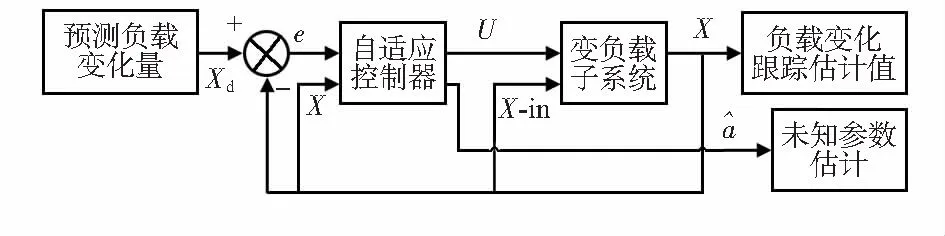
图3 自适应估计负载变化量结构框图

Step1 以负载质量变化为例设计预期量为x1d，则对其的跟踪误差表示为

e1=x1d-x1

(11)

求跟踪误差变化率，并将式(10)代入可得

(12)

式中u1为虚拟控制器输入函数。

Step2 为使跟踪误差收敛，选取Lyapunov函数

(13)

对其求导，可得

(14)

(15)

(16)

代入式(14)可得

(17)

将式(15)代入式(13)可得线性化反馈为

再由式(12)可得虚拟控制器输入函数为

(18)

Step3 设计实际控制输入u2，使得控制器能适应变负载系统中任意未知参数a。则a的估计误差可表示为

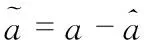
(19)

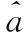
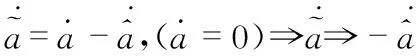
(20)

Step4 选取Lyapunov函数

(21)

对上式求导并结合式(18)～式(20)整理可得

(22)

(23)

(24)

由上式可得实际控制输入函数为

(25)

(26)

然后，结合估计的负载质量变化量和机体质量求得高度控制通道的补偿系数为

(27)

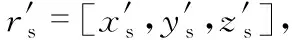
(28)

式中Ib,Is分别为三轴机体质心转动惯量和负载质心转动惯量。

2.2 跟踪微分器

以横滚角φ为例，设计非线性二阶跟踪微分器(tra-cking differentiator,TD)表达式如下

(29)

式中φd1为期望输入横滚角φd的跟踪信号，φd2为φd1微分信号，R为收敛速度因子。

采用二阶离散系统的快速最优综合函数，u=fhan(φd1-φd，φd2，R,h)如下

(30)

式中R为速度因子，h为积分步长，积分步长h越大振荡幅度越大。

2.3 扩张状态观测器

设计扩张状态观测器(extended state observer,ESO)表达式如下

(31)

为防止出现较大误差影响系统增益,并提升系统抗扰性，为此设计改进型nFal函数表达式如下

(32)

2.4 模糊非线性状态误差反馈控制律

设计模糊NLSEF表达式如下

(33)

式中e1,e2为误差及误差微分信号；β1,β2类似反馈误差的比例微分调节系数；b为补偿因子；u0为状态误差反馈控制量，u为最终控制量。

由于状态误差反馈参数常需根据被控对象实时状态进行手动调参，自适应能力受限。为此设计以e1,e2作为模糊输入量,利用模糊逻辑控制规则在线调节状态误差反馈参数，得到模糊控制器输出为Δβ1,Δβ2，实现在线实时自动调节参数并逐步逼近最优，提升系统控制效果。

规定以e1,e2为各自论域的5个模糊控制子集分别是{NB，NS，ZO，PS，PB}，并采用三角形隶属度函数，应用Mamdani型模糊推理原则，设计出Δβ1和Δβ2模糊规则表如表1、表2所示。

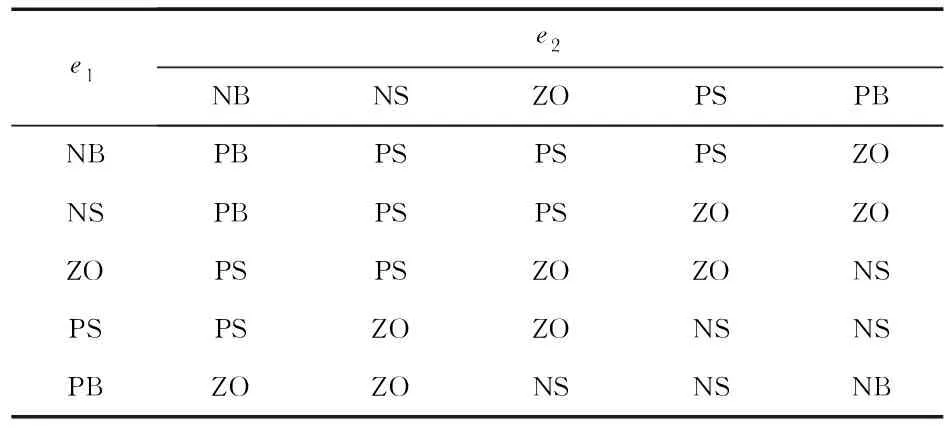
表1 Δβ1模糊规则

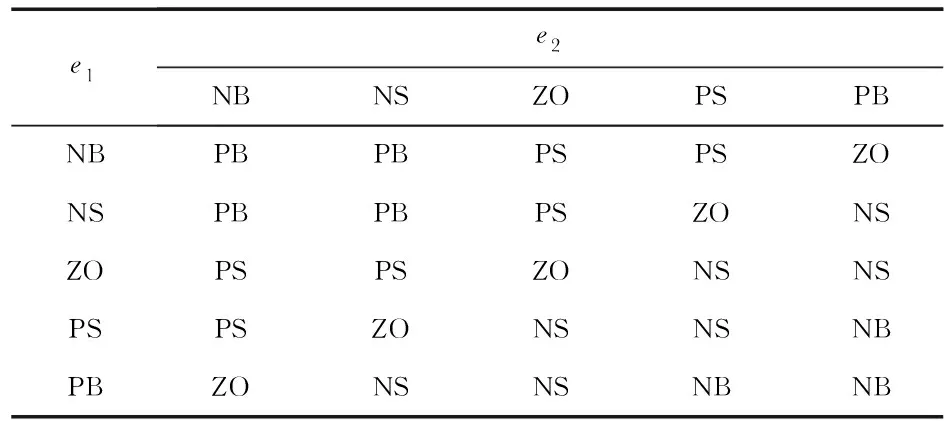
表2 Δβ2模糊规则

根据模糊推理规则，最终修正反馈误差控制律的增益系数为

(34)

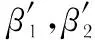
3 实验与结果分析

在MATLAB/Simulink环境中搭建变载荷四旋翼无人机模型，再设计串级PID控制、自适应反步法、ADRC算法以及AFADRC算法进行飞行稳定性对比实验。最后，通过STM32硬件开发平台作为飞控系统实际飞行验证本文算法的可靠性。具体变载荷无人机参数取值如表3。

表3 四旋翼无人机参数

3.1 Simulink仿真对比及分析

设定无人机初始飞行高度为1 m保持3 s再升到3 m位置稳定3 s后降回至2 m位置定高飞行，并在t=7 s时增加负载质量为ms=0.25 kg。模拟飞行中出现负载摆动的变质心情况，在负载质心偏移机体坐标系XY轴的基础上加正弦信号模拟负载摆动。则负载质心距离分别为Xs=Ys=7.5+2.5sinω,Zs=15 cm。自适应控制对变负载系统的估计和四种算法的高度及其姿态角控制效果对比曲线,如图4、图5所示。

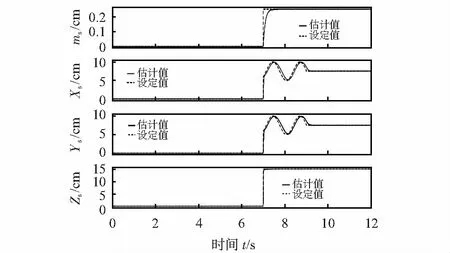
图4 负载变化量估计

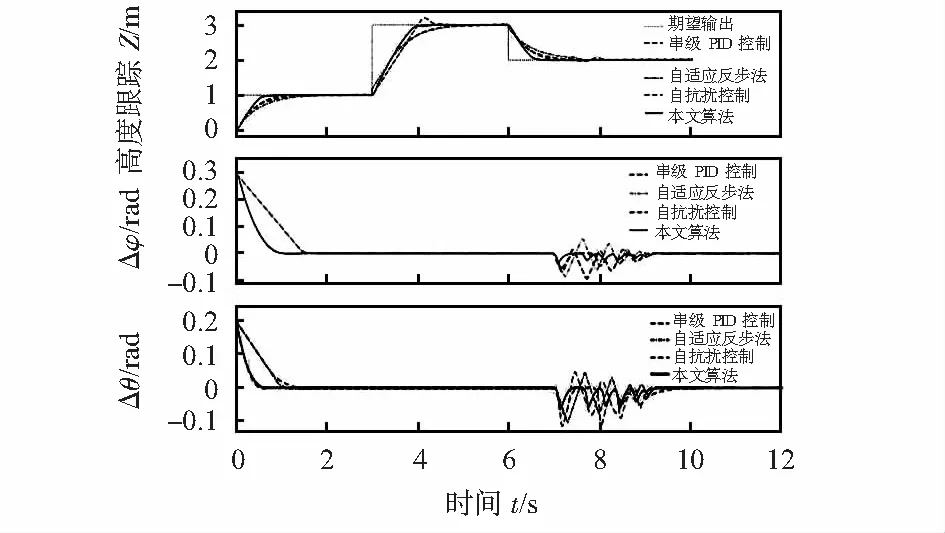
图5 三段高度变化及姿态角跟踪误差

由图4可知，对于负载质量以及质心沿坐标系XY轴摆动偏移量，自适应控制都可快速准确估计出负载系统变化量。由图5可知，对于在飞行过程中改变四旋翼无人机飞行高度以及增加负载质量和偏心摆动干扰，本文算法的高度跟踪以及姿态控制效果依然表现较好，高度变化响应时间约为0.6 s，姿态角的误差变化幅度基本保持±4°以内，相比其他三种算法的响应速度提高了45 %，姿态角综合动态稳定性提高了约50 %。

3.2 户外变载荷飞行实验

实验中，四旋翼无人机飞行姿态信息、高度信息数据通过Radio Telemetry无线数传装置实时反馈至地面上位机。用黑盒装载0.25 kg可滚动物体至于机体偏心位置作为变负载，进行空中定点定高保持稳定飞行控制实验。图6为无人机携变负载飞行，其中，负载挂于机体的质心偏移量范围为x=±10 cm,y=±10 cm。在携偏心负载保持飞行稳定一段时间后，空中释放负载验证负载质量变化时，机体姿态及高度稳定性情况。

图6 携带变负载飞行

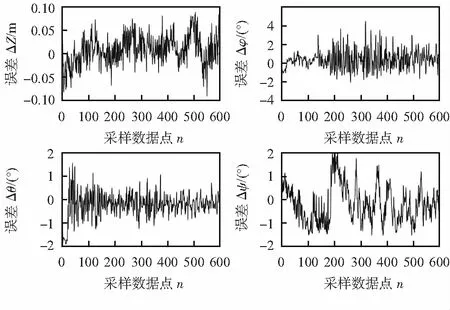
图7 实物飞行高度及姿态角误差

实际飞行实验结果如图7所示，根据无人机携变负载飞行状态下的测试结果可知高度误差，Δz=±0.08 m,且姿态角误差控制在±4°之内。因此，飞行器能很好的保持高度和姿态稳定，较好的验证了本文算法的有效性，同时也基本与仿真模型实验的结果保持一致。

4 结 论

综合实验结果，能够比较清晰地验证本文设计模型及改进算法的有效性。在不确定性变负载条件下本文算法都可以更稳定控制住无人机系统的飞行高度及姿态，同时验证了本文算法相比其他三种算法具有更快的响应速度，更好的鲁棒性以及应对不确定性变负载扰动的自适应能力更强。