结合扰动约束的低感知性对抗样本生成方法

王杨，曹铁勇*，杨吉斌，郑云飞,2,3，方正，邓小桐

1.陆军工程大学指挥控制工程学院，南京 210007；2.陆军炮兵防空兵学院南京校区火力系，南京 211100；3.安徽省偏振成像与探测重点实验室，合肥 230031

0 引 言

随着深度神经网络在计算机视觉任务中的广泛应用，对抗样本(adversarial examples)的概念也应运而生。对抗样本是指在原数据集中通过人工添加对抗扰动而形成的样本。这类样本会导致深度模型以高置信度给出与原样本不同的输出结果。对抗扰动是对抗样本生成过程中的关键因素。对抗扰动的作用是使模型产生错误的输出，同时扰动应尽量不影响原图像，甚至让人眼视觉也难以感知。

攻击成功率(attack success rate，ASR)和视觉感知性是评价对抗样本的两个重要指标。攻击成功率指添加扰动后对抗样本被深度模型误判的概率，其衡量了对抗样本对深度模型的攻击性能，数值越高，则对抗样本对深度模型的攻击能力越强。视觉感知性指在原图像上增加对抗扰动后而不为人眼视觉所感知的能力，其衡量了对抗样本的隐蔽性，感知性越低，说明对抗扰动越隐蔽，更不为人眼察觉。

按照对抗样本生成算法是否获得神经网络的参数和结构信息，可以将现有算法分为白盒攻击算法与黑盒攻击算法。

一些典型的白盒方法通过生成对抗样本实现了视觉的低感知性。FGSM(fast gradient sign method)算法(Goodfellow等，2015)在损失增加的方向上添加固定幅度的扰动生成对抗样本，但该算法仅在图像全局范围内添加扰动，没有对扰动的分布进行界定。Kurakin等人(2016)提出了基于FGSM的迭代版本BIM(basic iterative method)，经迭代沿损失增加的方向上添加小幅扰动，并在每次迭代后重新计算优化方向，进而构建了比FGSM更精细的扰动。之后FGSM衍生算法的目标也多是提升对抗性与迁移性(Dong等，2018；Xie等，2019；Shi等，2019)，在视觉感知性上与原有方法无明显差异。DeepFool算法(Moosavi-Dezfooli等，2016)通过比较样本空间中样本点到不同分类边界的距离，添加最小幅度的扰动生成对抗样本，它也成为白盒方法中视觉感知性比较的一个基准。JSMA(Jacobian-based saliency map attacks)(Papernot等,2016)计算图像显著性分数，依照像素点对输出结果的重要性添加扰动，仅改变部分图像像素即可实现攻击。C&W(Carlini &Wagner)算法(Carlini和Wagner，2017)使用改进的范数损失对扰动进行优化。Rony等人(2019)对C&W算法进行改进，在提升效率的同时仍能得到与原始算法视觉感知性近似的样本。Croce和Hein(2020)分析了现有方法在迭代时存在的次优解现象，提出了APGD(auto projected gradient descent)和AutoAttacks两种方法。PerC-C&W(perceptual color distance C&W)(Zhao等，2020)在CIELch空间计算对抗样本与原图像在样本空间的距离，为改善对抗样本的视觉感知性提供了新思路。

现实中常常无法获得部署模型的参数信息，因此黑盒方法的实用性要远大于白盒攻击方法。不同于白盒中普遍使用梯度信息生成扰动的做法，黑盒方法通过向模型输入带有扰动的图像，利用输出的变化求解扰动。这使得黑盒算法生成对抗样本的难度更大。OnePixel(Su等，2019)利用差分进化法筛选添加扰动的像素。该方法在极端情况下仅改变一个像素的数值就使深度模型输出错误，但扰动的生成位置没有考虑对视觉感知性的影响，且若要达到较高的攻击成功率需增加扰动像素的个数。Xiao等人(2018)提出了基于生成对抗网络(generative adversarial network，GAN)(Goodfellow 等，2014)的对抗样本生成方法AdvGAN(adversarial GAN)，使用合页损失优化扰动，并对扰动幅度进行限定。之后的AdvGAN++(Jandial等，2019)、DaST(data-free substitute training for adversarial atacks)(Zhou等，2020)方法均基于GAN网络。Phan等人(2020)提出CAG(content-aware adversarial attack generator)方法，利用感知损失生成对抗样本。此外，还有利用集成思想(Liu等，2017；Che等，2019；Pang等，2019)实现黑盒攻击的方法。这些方法在对抗样本的攻击成功率或攻击可行性上取得了进步，但在视觉感知性上的优化手段与之前的方法相同。

在达到一定攻击率的情况下，上述算法通过添加固定幅度的扰动、修改少量像素的数值或限定扰动变化的极限值实现对视觉感知性的客观要求。但客观上满足感知性要求，并不能在主观评价上取得很好的效果。

图1展示了部分算法生成的对抗样本。可以看出，现有方法在视觉感知性上还存在一定的改进空间：1)在图像全局增加扰动，存在扰动纹理突出的现象(图1(b)(d))；2)没有考虑生成扰动对全局结构的影响，破坏了图像的整体结构(图1(c));3)扰动分布不合理，生成扰动跨越前后背景(图1(d))。

图1 部分方法在Tiny-ImageNet数据集上生成的对抗样本Fig.1 Adversarial examples generated by some algorithms on Tiny-ImageNet((a) original image;(b) FGSM;(c) PerC-C&W;(d) AdvGAN)

限定对抗扰动的幅度、面积与分布，能够降低对抗样本的视觉感知性，但会对样本的攻击成功率产生影响。如何平衡对抗样本攻击成功率与视觉感知性之间的关系，在维持较高攻击成功率的前提下降低视觉感知性，是本文研究的主要问题。

综上，本文提出通过提取图像中的关键区域在有限的区域内添加扰动，同时限定对抗扰动在该区域内的分布，使扰动分布更符合图像全局结构，从而降低视觉感知性。已有研究(Selvaraj等，2017)证明，不同区域对模型输出结果的响应不尽相同。本文将图像中对模型分类结果响应较大的区域称为关键区域。在关键区域上添加对抗扰动能对模型的输出结果产生较大影响，从而维持受限扰动条件下对抗攻击的ASR。

本文方法具体分为两个阶段。第1阶段的目标是使用提取网络提取对分类模型输出影响较大的关键区域。若提取出的区域符合预期，则向该区域添加扰动，能加大分类模型输出错误结果的概率。为训练提取网络，在第1阶段不对扰动进行优化，使用数值固定的噪声作为第1阶段扰动，训练提取网络；同时，计算关键区域与输入数据在感知网络某一层输出的感知损失(杨娟 等，2019)，从而优化提取网络，使提取出的区域与输入数据在图像全局结构近似。第2阶段固定提取网络的权重，生成关键区域，通过生成对抗网络向关键区域添加扰动，生成对抗样本。生成对抗网络是一种基于对抗性训练的神经网络，由生成网络和判别网络两个子网络构成。在本文中，生成网络的功能是输入图像信息，输出针对该图像的对抗扰动。之后对抗扰动与原图像结合，成为对抗样本。将对抗样本与原始图像送入判别网络，由网络判断输入数据是原始数据还是对抗样本。随着两种网络的交替训练，扰动的性能逐步提升。

为验证本文生成对抗样本的视觉感知性，引入均方误差(mean square error，MSE)与结构相似性(structural similarity，SSIM)作为衡量感知性的两个客观指标。最终在3个公开数据集上的实验验证了本文方法的有效性，在保持较高攻击成功率的同时，有效限制了扰动生成的区域与面积，显著降低了视觉感知性。

1 本文算法

1.1 问题描述

给定原始图像x,y为正确的分类标签，图像分类模型f能够以较大概率实现从输入x至输出y的映射f(x)→y。向原始图像x添加扰动ρ生成对抗样本x+ρ,使得f(x+ρ)≠y。

1.2 方法介绍

本文算法提出通过约束对抗扰动的面积与空间分布，降低对抗样本的视觉感知性。算法在设计中主要考虑以下因素：1)对抗扰动分布尽可能在图像的同一语义区域，如目标区域或背景区域；2)扰动分布应与图像结构保持一致；3)减少无效扰动的生成。

模型包含两个阶段，总体框架如图2所示，其中，橙色表示在某一阶段进行训练的网络，蓝色表示在该阶段权重固定的网络。在第1阶段，通过提取网络提取能显著影响深度模型输出结果的关键区域，并利用感知损失进一步限定该区域，使扰动与图像的结构信息保持一致。在第2阶段，通过带有自注意力机制的生成对抗网络，向前一阶段获得的图像关键区域添加扰动，生成具有低感知性的对抗样本。

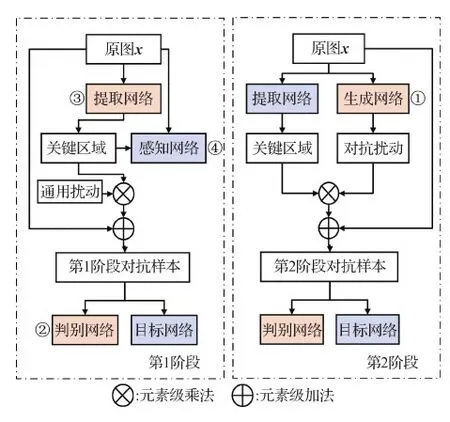
图2 总体框架Fig.2 Overall framework

第2阶段生成扰动的对抗性应优于或等于第1阶段使用的噪声扰动，这也为第2阶段的对抗成功率划定了下界。同时，对抗成功率的下界也与第1阶段选择的扰动相关。本文选择高斯噪声作为第1阶段的固定扰动。

1.3 生成对抗网络

模型中通过生成对抗网络向原图添加扰动，构造对抗样本。具体而言，本文生成网络包含编码器—瓶颈层—解码器结构。瓶颈层使用残差连接，编码器包含6层卷积—标准化—激活结构，瓶颈层残差分支包含4层卷积—标准化—激活结构，解码器包含5层结构。生成网络结构如图3所示。

为使生成的对抗扰动更平滑，模型在解码器结构图的模块2①中引入像素渲染模块(Shi等，2016)，如图3右上标注A所示，计算流程为：输入尺寸为H×W×r2的特征图，通过周期筛选得到尺寸为rH×rW×C的高分辨率图像。本文在生成网络的瓶颈层加入自注意力机制，如图3右上标注B所示。自注意力机制是注意力机制的一种，它擅长捕捉数据或特征的内部相关性。在图像生成领域中，它可以捕捉图像中某一点像素与其他位置较远像素间的联系，更好地对全局信息建模，具体结构如图4所示。

图3 生成网络结构图Fig.3 Generator structure

图4 自注意力结构Fig.4 Self-attention module

图5展示了自注意生成网络与普通生成网络生成扰动的对比，其中图5(b)(c)均为标准化后灰度图像。从图中红框区域可以看出，使用自注意力机制与全局感知损失生成的扰动主要分布在图像的关键区域，且分布更为均匀、密集。从图中蓝框区域可以看出，在非关键区域添加的扰动颜色较浅、幅度更小。

图5 自注意生成网络与普通生成网络生成扰动的对比Fig.5 Comparison of adversarial perturbations between self-attention generator and normal generator((a) original images；(b) perturbation generated with self-attention mechanism；(c) normal perturbation)

判别网络判断输入数据是原始样本或是对抗样本。网络包含5层结构，前3层使用谱标准化，用以提升网络训练时的稳定性，结构如图6所示对应图2中模块②。

图6 判别网络结构Fig.6 Discriminator’s structure

1.4 提取网络

算法的出发点是通过限定扰动的位置与分布，降低对抗样本的视觉感知性。注意力机制(项圣凯等，2020)能够提取出深度模型输出的关键区域，赋予其更大权重。算法通过带有注意力机制的提取网络，生成关键区域，约束扰动的分布。

提取网络与注意力机制的结构如图7所示，其中D-Conv表示空洞卷积结构，Conv为卷积结构对应图2中模块③。注意力机制选择应用广泛的BAM(bottleneck attention module)(Park等，2018)结构。提取网络包含3层卷积—标准化—激活结构、1个注意力层、2个反卷积—标准化—激活结构和1个用于增强局部信息的池化—卷积—标准化—激活结构。通过提取网络中卷积结构得到的输出特征图，经过门机制筛选，最终得到包含图像关键区域的特征图。门机制筛选图像关键区域算法的具体步骤如下：

图7 提取网络与注意力结构Fig.7 Extractor and attention mechanism

输入：图像x。

输出：包含图像关键区域的特征图。

第1阶段：图像x送入注意力网络生成标准化特征图。

1) 将图像送入注意力网络，输出注意力特征图(H×W× 3);

2) 将注意力特征图通道内像素的值归一化至[0,1]。

第2阶段：门机制生成粗特征图，筛选后得到关键区域。

3) for 注意力特征图中的像素点(x,y,c) do;

4) 粗特征图在 (x,y) 的值为该点在第1阶段生成特征图的值 (1 × 3) 与τ(3 × 1)相乘;

5) if 值大于阈值;

6) 值不变;

7) else;

8) 值为0;

9) end for;

10) 得到关键区域特征图。

经实验验证，τ的取值为[0.36,0.34,0.30]，阈值设定为0.7。

1.5 感知网络结构

为更好地约束注意力网络生成的关键区域，本文引入感知损失。计算感知损失所用的特征提取网络为带有ImageNet预训练权重的VGG16(Visual Geometry Group)网络，对应图2中模块④。

2 训练过程

2.1 第1阶段训练过程

第1阶段训练注意力网络，损失函数为

L1=α1Ladv1+β1LD1+γ1Lp

(1)

式中，Ladv1为第1阶段对抗损失，LD1为第1阶段判别损失，Lp为感知损失，α1、β1、γ1的取值分别为5、10、1。

原图进入注意力网络，生成包含图像关键区域的特征图。原图与特征图进入感知网络，计算两者的感知损失。感知损失为特征图与原图在经过感知网络第2层激活函数后所得特征图间的最小二乘损失，表达式为

(2)

式中，φ为特征提取网络，C、H、W为原图x与特征图a经过特征提取网络第2层后的通道数、高度和宽度。

将通过门机制筛选得到的特征图与噪声扰动相乘，生成第1阶段对抗扰动。扰动与原图结合得到第1阶段的对抗样本。对抗样本和原图一同送入判别网络，计算判别损失。之后对抗样本送入目标网络，计算第1阶段对抗损失。

判别损失为

LD1=ExlogD(x)+Exlog(1-D(x+ρ1))

(3)

ρ1=F⊗PG

(4)

式中，ρ1为第1阶段得到的扰动，F为经过门机制得到的特征图，D()为判别器输出结果，PG表示高斯噪声扰动(Gaussian noise perturbation)，F与PG间使用元素级乘法⊗。

对抗损失表达式为

Ladv1=Exlt(T(x+ρ1),t)
ρ1∈[-Pmax,Pmax]

(5)

式中，T为被攻击的深度模型，输入第1阶段对抗样本，输出向量与经过one-hot编码所得的分类标签向量t长度相同。lt为损失函数，本文使用交叉熵损失。Pmax为扰动幅度的上限。

2.2 第2阶段训练过程

第2阶段训练生成网络，损失表达式为

(6)

式中，α2、β2、γ2的取值分别为5、1、1。固定提取网络权重，将原图送入提取网络与生成网络，生成带有关键区域的特征图和第2阶段对抗扰动。扰动与特征图之间进行元素级乘法，并与原图结合，生成对抗样本。将原图与对抗样本送入目标网络和判别网络，计算对抗损失和判别损失。

第2阶段的对抗损失为

Ladv2=Exlt(T(x+ρ2),t)

(7)

ρ2=F⊗P2,ρ2∈[-Pmax,Pmax]

(8)

式中，ρ2为第2阶段得到的扰动，P2为生成网络生成的第2阶段扰动(perturbation generated by generator)。第2阶段的判别损失为

LD2=ExlogD(x)+Exlog(1-D(x+ρ2))

(9)

在两个阶段中，算法均对判别网络进行训练。两个阶段的判别网络结构相同，作用是判断输入数据是原始数据还是添加扰动后的数据。第1阶段训练结束后，不固定判别网络的参数，直接进入第2阶段的训练。实验结果表明，在前一阶段得到的权重上继续训练与在初始化后的网络上重新训练相比，能更快地使模型收敛。随着轮数的增加，两种条件下训练得到的损失趋于一致，对应的攻击成功率无明显差别。

3 实验与分析

为评估本文算法的效果，与9种典型对抗样本算法在3个图像分类数据集上进行比较。对比算法包含白盒与黑盒算法，白盒算法为FGSM (Goodfellow 等，2015)、BIM(Kurakin 等，2016)、DeepFool(Moosavi-Dezfooli等，2016)、JSMA(Papernot 等，2016)、PerC-C&W (Zhao 等，2020)、APGD(Croce和Hein，2020)和AutoAttack(Croce和Hein，2020)，黑盒算法为OnePixel(Su 等，2019)和AdvGAN (Xiao 等，2018)。

3.1 评估数据集及模型

本文方法使用的优化器为Adam，判别损失学习率为0.005，对抗损失学习率为0.01，采用异步优化策略，即判别网络每5轮进行1次优化、生成网络每轮进行优化。两个阶段的迭代轮数均为100轮。评估数据集为CIFAR-10、Tiny-ImageNet和随机抽取的 ImageNet数据集图像。CIFAR-10数据集共10种类别，包含50 000幅训练图像和10 000幅测试图像，分辨率为32 × 32像素。Tiny-ImageNet数据集共200种类别，包含100 000幅训练图像和10 000幅测试图像，分辨率为64 × 64像素。随机选取ImageNet数据集共10种类别，包含1 000幅图像，分辨率裁剪为224 × 224像素。对抗模型为3种广泛使用的图像分类模型：VGG13、ResNet18和DenseNet121。实验硬件平台为 GeForce Nvidia RTX 2080Ti，软件平台为Ubuntu 19.10、Pytorch 1.6。

在客观指标的评价上，使用ASR评价算法的对抗性能，通过比较对抗扰动前后图像的MSE和SSIM衡量不同算法生成对抗样本的客观视觉感知性。MSE衡量对抗扰动的强度，SSIM从结构化信息角度评价对抗扰动对图像的影响。ASR与SSIM数值越接近1越好，MSE数值越小越好。FGSM的扰动步长ε= 10，APGD与AutoAttack的扰动步长均为15。其余对比算法参数为原文开源代码的默认参数。对比算法均设置最大迭代轮数。

3.2 攻击效果对比分析

实验对不同对抗样本的攻击效果进行对比与分析。不同方法在CIFAR-10和Tiny-ImageNet数据集上的ASR比较如表1和表2所示。

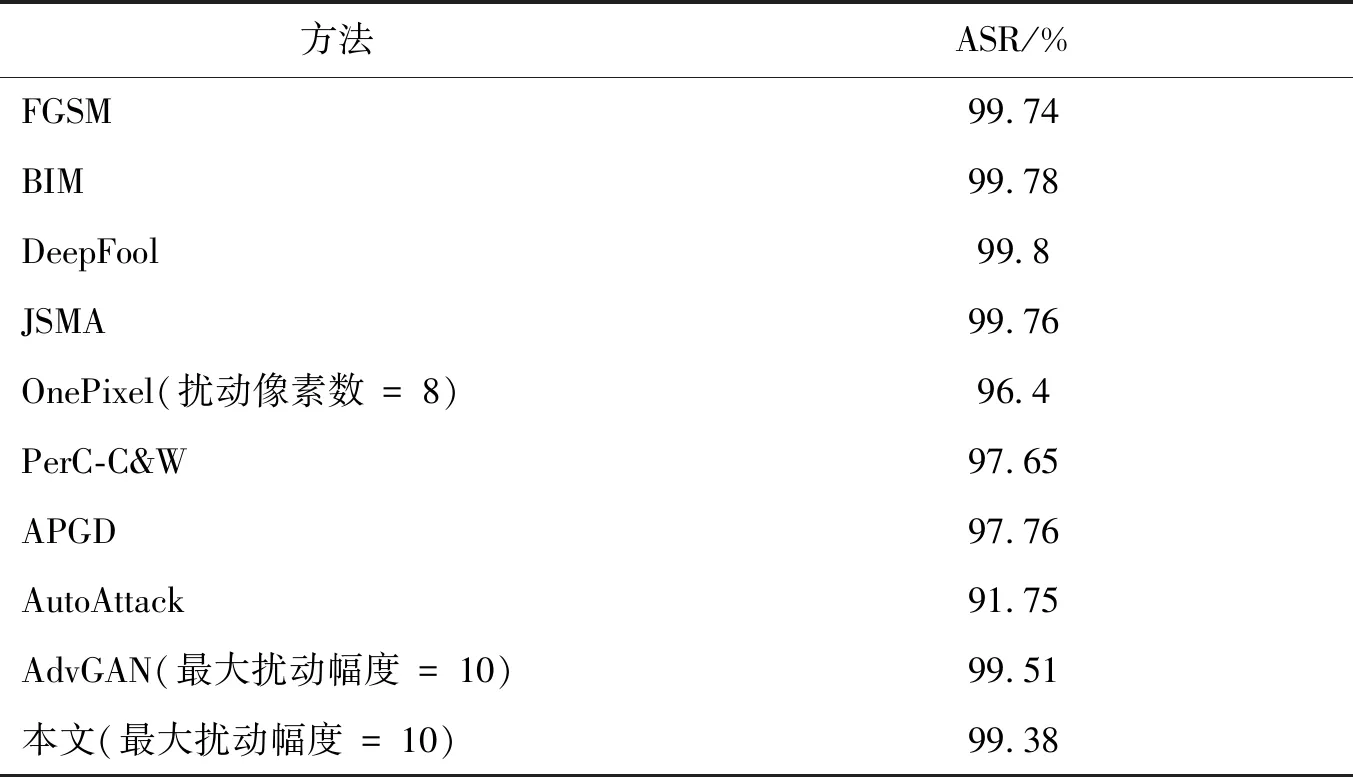
表2 不同方法在Tiny-ImageNet数据集的ASR比较Table 2 ASR comparison of different methods on Tiny-ImageNet dataset

从表1可以看出，在低分辨率数据集CIFAR-10上添加小幅度扰动，随着扰动幅度的增强，ASR逐渐提升，与基于GAN的算法相差不超过3%，而在ResNet网络上甚至超过了基于GAN的算法。原因是在分辨率较低的图像上，注意力网络生成的图像重点区域较小，添加小幅扰动能降低模型的分类置信度，但仍输出正确的结果。

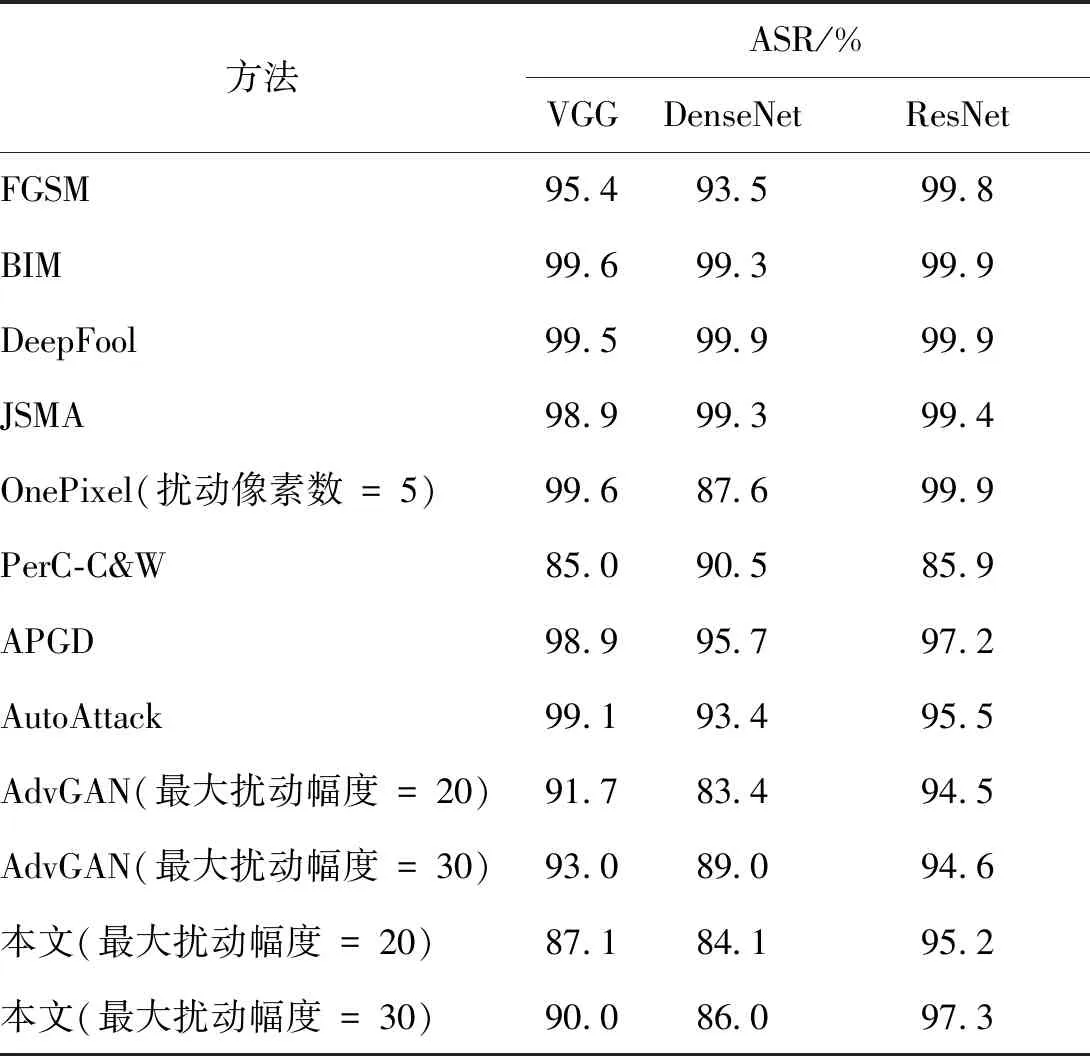
表1 不同方法在CIFAR-10数据集的ASR比较Table 1 ASR comparison of different methods on CIFAR-10 dataset

从表2可以看出，随着图像分辨率的增长(Tiny-ImageNet、ImageNet)，注意力网络提取的图像重点区域增大，在小幅度扰动的情况下，本文方法的对抗攻击成功率能够与对比方法持平，相差不超过0.5%；另外由于攻击成功率超过99%，微小的性能差别并不会影响实质攻击效果。综合比较，本文方法的攻击成功率与当前方法近似，维持在同一水平。

3.3 视觉感知性对比分析

3.3.1 客观指标分析

不同方法在CIFAR-10和Tiny-ImageNet数据集上的MSE比较如表3所示。可以看出，本文方法的MSE值大幅低于FGSM、BIM、PerC-C&W、APGD、AutoAttack和AdvGAN。DeepFool算法的MSE值远低于其他算法，原因是Tiny-ImageNet数据集有200个类别，算法能够找到更多的决策边界，进而选择更小的边界距离，减小扰动的幅度。PerC-C&W的MSE远大于其他方法，原因是算法并不在图像的每一通道限制扰动幅度，而是限定在三通道上总的扰动幅度，导致其扰动数值分布不平均，MSE较大。OnePixel和JSMA对像素值的修改幅度剧烈，使得MSE数值偏大。这也反映了客观的评价指标并不能充分体现主观的感知性评价。APGD通过改进现有方法的不足，AutoAttack通过糅合多种方法提升对抗攻击的成功率，但均没有充分考虑扰动对图像感知性的影响，故客观感知性评价较低。综上，在低、中分辨率数据集上对视觉感知性的客观评价指标比较表明，本文方法的MSE值优于大部分比较方法，仅在中分辨率数据集上高于DeepFool方法。

表3 不同方法的MSE比较Table 3 MSE comparison of different methods

结构相似性(SSIM)是一衡量两幅图像相似度的指标，其值越接近1，说明两幅图像越相似。不同方法在CIFAR-10和Tiny-ImageNet数据集上的SSIM比较如表4所示。可以看出，本文方法的SSIM较AdvGAN大幅提升，略高于DeepFool算法。

表4 不同方法的SSIM比较Table 4 SSIM comparison of different methods

3.3.2 主观感知性比较

图8为不同方法在CIFAR-10数据集上生成的对抗样本比较，其中，为确保攻击成功率，OnePixel方法修改的像素点为5个。图8(j)为AdvGAN方法在扰动幅度Pmax= 10时生成的对抗样本，图8(k)和图8(l)分别为本文方法在扰动幅度Pmax=20和Pmax=30时生成的对抗样本。可以看出，本文方法在扰动幅度Pmax=20时较扰动幅度Pmax= 10的AdvGAN方法仍有一定的优势。

图8 不同方法在CIFAR-10数据集上生成的对抗样本比较Fig.8 Comparison of different adversarial examples on CIFAR-10 ((a) original images;(b) FGSM;(c) BIM;(d) DeepFool；(e) PerC-C&W;(f) OnePixel;(g) JSMA;(h) APGD;(i) AutoAttack;(j) AdvGAN when Pmax= 10;(k) ours whenPmax= 20;(l) ours whenPmax= 30)

图9为不同方法在Tiny-ImageNet数据集上的效果比较。其中，图9(j)和图9(k)分别为扰动幅度Pmax= 10时AdvGAN和本文方法生成的对抗样本。可以看出，在扰动幅度相同情况下，与黑盒方法OnePixel和AdvGAN相比，本文生成扰动面积小，对抗纹理不明显；与白盒方法中的FGSM、BIM和PerC-C&W方法相比，本文扰动纹理的感知性更低。

图9 不同方法在Tiny-ImageNet数据集上生成的对抗样本比较Fig.9 Comparison of different adversarial examples on Tiny-ImageNet((a) original images;(b) FGSM;(c) BIM;(d) DeepFool;(e) PerC-C&W;(f) OnePixel;(g) JSMA;(h) APGD;(i) AutoAttck;(j) AdvGAN when Pmax= 10;(k) ours when Pmax= 10)

在包含1 000幅挑选的ImageNet图像数据集上对本文方法的视觉感知性进行测试，扰动幅度限制为25，在保持较高成功率的情况下，视觉感知效果如图10所示。可以看出，1)限定最大扰动幅度为15时，本文方法的效果(图10(k))与AdvGAN(图10(j))相比，随着分辨率的提升，对抗扰动的纹理对图像信息、结构和视觉感知性产生的影响降低，但AdvGAN生成的对抗样本在图像边缘产生了一定的虚化。2)在高分辨率图像上与对比方法相比，本文方法在视觉感知性上低于FGSM、JSMA、AdvGAN算法，与BIM、DeepFool、PerC-C&W、OnePixel、APGD和AutoAttack算法相当。

图10 不同方法在ImageNet数据集上生成的对抗样本比较Fig.10 Comparison of different adversarial examples on ImageNet dataset((a) original images;(b) FGSM;(c) BIM;(d) DeepFool;(e) PerC-C&W;(f) OnePixel;(g) JSMA;(h) APGD;(i) AutoAttack;(j) AdvGAN;(k) ours)

3.4 参数敏感性分析与消融实验

3.4.1 参数敏感性分析

对扰动生成产生影响的参数主要有扰动幅度Pmax、第1阶段训练参数和第2阶段训练参数。其中，第1阶段训练参数包括对抗损失权重α1=5、判别损失权重β1=10、感知损失权重γ1=1；第2阶段训练参数包括对抗损失权重α2=5、判别损失权重β2=1、感知损失权重γ2=1。实验对第1、2阶段的训练参数进行敏感性分析，并对算法中各模块对ASR的影响做消融实验。选用数据集为Tiny-ImageNet，对抗模型为ResNet18，扰动最大幅值Pmax=10。

对于两个阶段的6个参数，分别对某一参数进行调整，固定其余参数，观察算法ASR值的变化。对第1阶段参数进行分析，结果如图11(a)—(c)所示。从ASR变化的幅度可以看出，对抗损失权重α1对ASR影响较大，随着α1增大，算法ASR逐渐增加，表明算法侧重于对模型的攻击性能。随着判别损失权重β1和感知损失权重γ1的增加，ASR下降，模型趋于对扰动的分布进行优化，对抗性能下降。在第1阶段训练结束后，不对判别网络权重进行初始化，而是直接进行下一阶段的训练，结果如图11(d)—(e)所示。第2阶段的判别损失权重β2对ASR的影响较小。在该阶段主要对生成网络进行训练，对抗损失权重α2对ASR产生较大影响。从图11的数据观察得到，若侧重于对抗样本的视觉感知性(降低对抗损失权重、提高判别损失权重)，则攻击成功率有所下滑，体现出提升对抗样本的攻击成功率与减低其视觉感知性之间是矛盾的。若仅进行第1阶段训练，得到的攻击成功率并不理想；第2阶段对扰动进行优化后，攻击成功率得到提升。说明第2阶段的功能是对第1阶段使用固定扰动提取出的关键区域生成新的扰动，新生成的扰动更适应该区域所包含的图像信息。

图11 参数变化对ASR的影响Fig.11 The influence of α,β and γ on ASR ((a) α1-ASR line graph;(b) β1-ASR line graph;(c) γ1-ASR line graph;(d)α2-ASR line graph;(e)β2-ASR line graph;(f)γ2-ASR line graph)

3.4.2 消融实验

参与第1阶段训练的模块主要有感知网络和注意力网络，两种模块对ASR的影响如表5所示。

表5 不同模块对ASR的影响Table 5 The influence of different modules on ASR

4 结 论

本文分析了现有对抗样本生成方法在视觉感知性上的不足，提出了全新的低感知对抗样本生成方法，通过限定对抗样本扰动生成的位置与面积，在保证攻击率的情况下，显著降低了对抗样本的视觉感知性。最后通过定性和定量实验，比较了本文算法与具有代表性的对抗样本方法在攻击成功率和视觉感知性上的性能，验证了本文算法的有效性。

本文主要针对对抗样本的视觉感知性进行研究，通过约束扰动的位置与分布提升了对抗样本的视觉效果。下一步工作将关注于提升对抗样本的攻击成功率，增强攻击的鲁棒性。