基于加窗的相位相关的多谱段图像匹配
张文琪,刘本永
(贵州大学 大数据与信息工程学院,贵阳 550025)
0 引 言
图像匹配是对表示同一个场景的两幅图像在空间上进行对准确定映射关系的过程。图像匹配技术是计算视觉领域的基本问题,是图像分析和处理的基础。多谱段图像匹配是指在不同类型传感器获取的图像之间进行的匹配,如可见光与红外图像匹配、可见光与合成孔径雷达(Synthetic Aperture Radar,SAR)图像匹配等。
随着遥感技术的发展,获取SAR图像方式越来越多,SAR图像具有全天候、全天时的探测能力,且其穿透力强不受天气、云层等因素的影响。可见光图像具有分辨率高、形状纹理信息清晰且色彩丰富的特点、但是其成像质量很容易受光照变化和天气等因素的影响,抗干扰能力较弱。不同的传感器形成的图像可以表示同一场景下不同特征和属性信息,SAR图像和可见光图像可以互补信息。因此,SAR图像与可见光图像的结合对于提供高度互补的观测场景信息具有重要意义,可以有效地弥补单一模型的不足。多谱段图像匹配一直是图像匹配中的一个难点,其被广泛应用于变化检测、图像融合、导航导制等多个方面。
图像匹配主要分为基于像素灰度的匹配方法和基于特征的匹配方法。基于特征的匹配方法主要是提取图像中点、线、面等特征并生成特征描述子,通过相应的距离度量方法寻找特征间的对应关系,该方法具有匹配速度快,抗干扰能力较强,灵活性较强等特点。这一类方法主要有SIFT特征匹配算法、Harris特征匹配算法、SURF等。基于灰度像素灰度的匹配方法主要是利用图像的灰度信息进行匹配,该方法计算过程相对简单,但是计算量较大,对噪声、光照和遮挡较为敏感。这一类方法主要有基于互相关的方法、傅里叶方法和互信息方法。傅里叶方法利用图像频域傅里叶变换表示。其中一个代表是基于傅里叶移位定理的相位相关方法,该方法最初是由Kuglin等人在1975年提出应用于图像匹配,这种方法首先分别对两张图像进行傅里叶变换,由时域将其变换到频域,在频域中计算互功率谱的相位差峰值来确定图像间的平移关系。该方法仅利用了两图像互功率谱的相位信息,能够很好地克服光照变化和噪声的影响,具有较强的鲁棒性和抗干扰能力,且计算速度较快,因此在图像匹配、图像拼接等多个方面应用广泛。但是该算法在实际的实现中需要对图像进行离散傅里叶变换,从而产生频谱泄露,其次图像的上下、左右存在差异,是不连续的,在进行傅里叶变换时会产生额外的高频干扰,产生边缘效应。受频谱泄露和边缘效应的影响,会导致相位相关函数的恶化,产生虚假平移峰值,从而导致多谱段图像匹配效果不佳。
本文针对多谱段图像匹配问题,探讨一种基于加窗预处理的相位相关算法,首先使用核回归方法构造二维圆对称窗函数;通过构造的二维窗函数对多谱段图像进行加窗预处理,以降低频谱泄露和边缘效应对多谱段图像匹配的影响,并将相位相关应用于图像匹配以计算图像间的相对平移;针对互功率谱逆变换后仍然存在多个虚假谱峰的现象,考虑到高频干扰和频谱混叠的影响,在进行相位相关后对互功率谱进行频域低通滤波处理以抑制虚假峰值。实验结果表明,本文所探讨的方法可以有效地提高多谱段图像匹配的准确性。
1 相位相关法
基于频域傅里叶变换相位相关原理是根据傅里叶变换平移理论。设同一场景的两幅图像和分别为参考图像和模板图像,两者之间有平移关系如式(1):
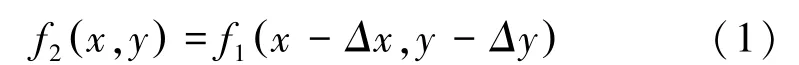
其中,(,)表示平移量。对两边同时进行傅里叶变换可得式(2):

其中,和分别表示图像、的傅里叶变换。
由式(2)可知,仅存在平移关系的两图像的傅里叶变换具有相同的幅值,仅相位不同,而图像和的归一化互功率谱定义如式(3):

将式(2)代入式(3),可得归一化互功率谱的表达式(4):

对式(4)进行傅里叶逆变换可得式(5):

综上可知,归一化互功率谱的相位等于两图像的相位差,通过求归一化互功率谱的傅里叶逆变换得到的二维冲击函数的峰值的偏移,可以确定两幅图像的相对平移(,)。
2 核回归二维圆对称窗函数
为了抑制频谱泄露和边缘效应,一般采取的方法就是加入缓慢变化的窗函数,如海明(Hamming)窗,高斯(Gaussian)窗等,使得时域信号边缘突变平滑些。现有的大部分窗函数分成幂窗、三角函数窗、指数窗。其中矩形窗是以时间为变量的零次幂窗,离散时域表达式(6)如下:
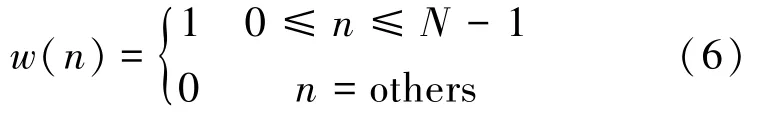
其中,表示窗函数长度。
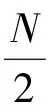

海明窗是一种三角函数窗,离散时域表达式(8)如下:
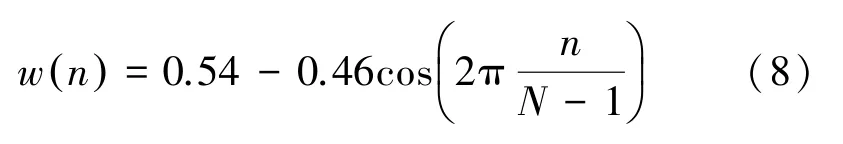
其中,0≤≤1。
高斯窗是一种指数窗,离散时域表达式(9)如下:


与矩形窗相比,海明窗、Bartlett窗、高斯窗在时域上由中心向边缘缓慢衰减,而在频域上旁瓣衰减较大,可以有效减小频谱泄露和边缘效应的影响,如图1所示。
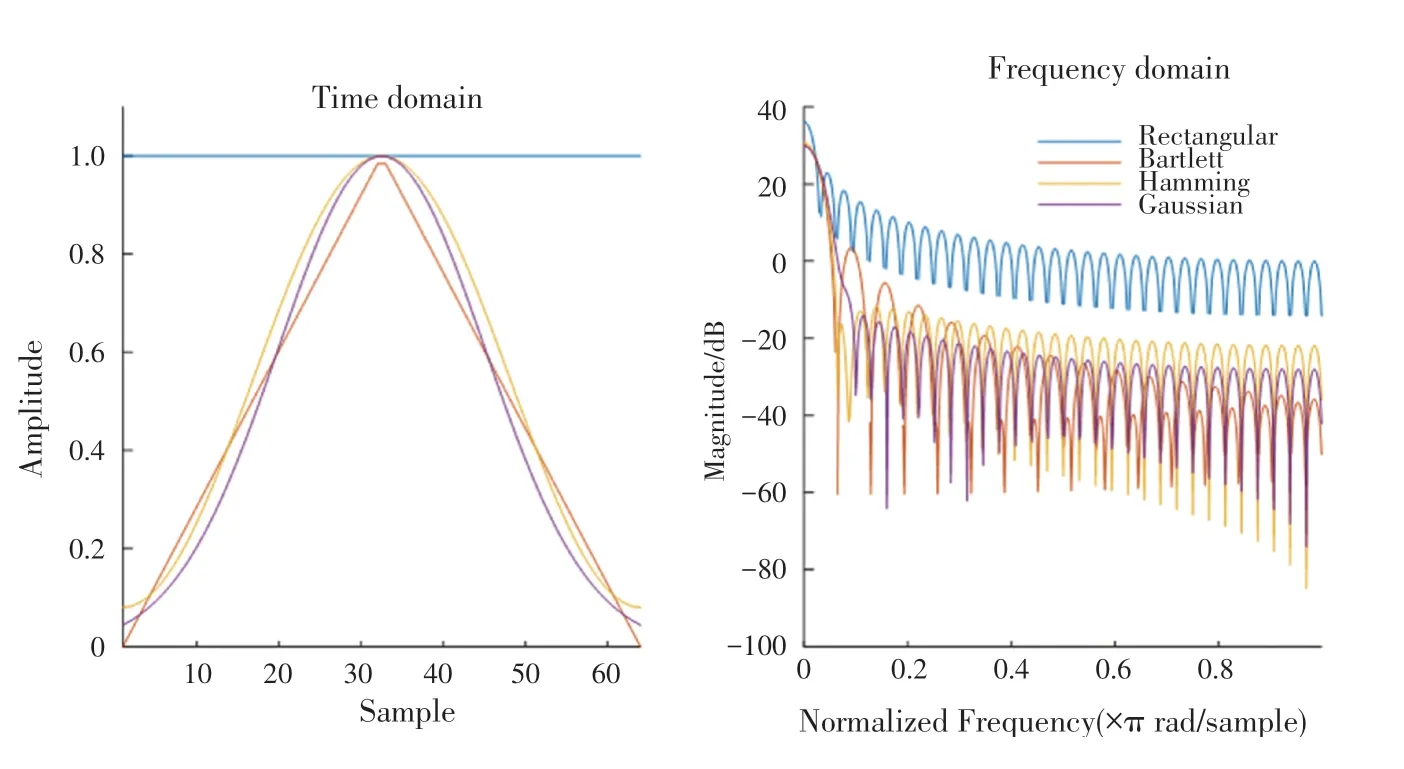
图1 时域频域窗函数对比Fig.1 Comparison of window functions in time domain and frequency domain
对图像加入二维hamming窗处理,使得边缘处突变较少、更加连续,从而削弱了边界效应的影响,如图2所示。

图2 图像加窗效果Fig.2 Image windowing effect
如果一维窗函数具有良好的性质,则可以通过一维窗函数来构造二维窗函数。一般构造方法有两种:乘积法是通过将两个一维窗函数直接相乘得到二维窗函数,称为可分离型窗函数,设()和()是一维窗函数,则二维可分离窗函数,式(10):

因该方法是直接将两个一维窗函数直接相乘得到一个参数矩阵,根据二维窗的性质,该方法不具有最优效果。1972年T.S.Huang提出通过旋转法得到二维窗函数,如果一维窗函数具有良好性质且对称,则是通过将一维窗函数进行旋转构造二维窗函数。对一维窗函数()进行旋转得到二维窗函数(,),式(11):
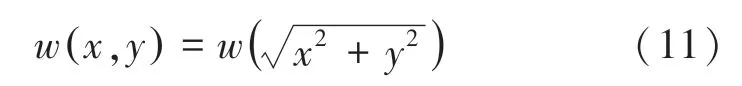
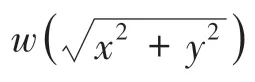
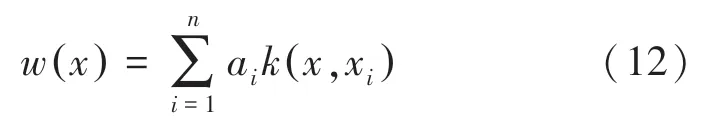
其中,为再生核Hilbert空间的核函数;为权值在一维窗中对应的位置;而x表示第项权值在一维窗中对应的位置;a为未知系数。
由其构成的系数向量可使用最小二乘准则估计得到,式(13):
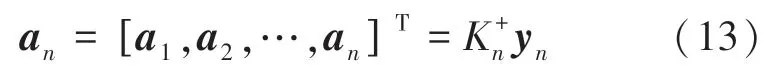
其中,表示矩阵的Moore-Penrose广义逆;K为行列的核矩阵;y为一维窗各权值构成的列向量。
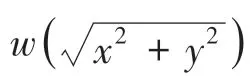
3 互功率谱低通滤波
由于匹配图像之间差异和SAR图像的噪声干扰,相位相关后的互功率谱进行傅里叶逆变换后仍然存在多个虚假峰值,而且在获取数字图像的过程需要对图像进行采样处理,根据奈奎斯特定理,当采样频率F小于图像模拟信号最高频率的2倍时,得到的频谱会包含原信号中频率大于F/2的频谱叠加,从而导致频谱混叠,如图3所示。可以通过低通滤波器对相位相关得到的互功率谱进一步处理,从而降低高频干扰对相位相关的影响。常用的频域理想低通转移函数如式(14):

图3 频谱混叠示意图Fig.3 Schematic diagram of spectral aliasing

其中,表示截止频率,并设min(,)*2;用于调节截止频率;和分别表示图像的高和宽;(,)是频域中点(,)到矩阵中心的欧式距离。
综上所述,将光学图像作为参考图像,SAR图像作为模板图像。本文的算法流程如下:
(1)对SAR图像进行滤波去噪,并对其进行边缘补零;
(2)分别对SAR图像和光学图像进行加窗;
(3)计算参考图像和模板图像的互功率谱;
(4)对互功率谱进行频域低通滤波;
(5)归一化互功率谱;
(6)傅里叶逆变换计算相位相关平面的极值点,得到两图像的平移量,从而确定匹配关系。
4 实验结果及分析
实验通过200对大小均为512×512的SAR-光学(OPT)图像,计算相位相关平面中的峰值位置得到两图像的相对平移,以预测匹配坐标。本文用正确匹配率(Correct Matching Rate,)评估匹配性能,式(15):

其中,表示图像匹配对数,N表示正确匹配个数。
通过两图像的匹配误差值()判定是否匹配,并设≤5时为正确匹配,计算如式(16):
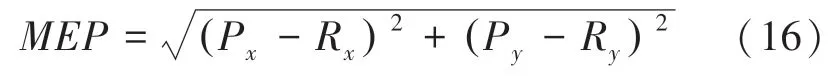
其中,P和P是预测的匹配点的像素坐标,R和R是标准的匹配点的像素坐标。
4.1 加窗对匹配的影响
由于SAR图像存在斑点噪声,本文采用中值滤波和双边滤波对SAR图像去噪,并用不同的窗函数进行实验。使用不同的滤波器和不同的窗函数进行实验的匹配结果见表1,w/oWindow表示无窗,有Rot表示用增量型核回归方式生成的窗函数,无Rot表示用乘积法生成的窗函数。结果表明,对SAR图像进行简单的中值滤波和双边滤波预处理也可以提高正确匹配率,加入窗函数后的相位相关算法的正确匹配率显著提高,且较乘积法生成的二维窗函数,增量型核回归方法生成的二维窗函数表现更好。

表1 原图像匹配结果Tab.1 Original image matching results
此外,当两图像之间存在平移关系,图像除了重叠区域外的信息都是冗余信息,而冗余的信息在计算相位相关时会产生额外的峰值。通过降采样降低冗余信息,并提高计算效率,现将200对SAR-光学图像进行降采样为300×300,得到表2。结果表明,虽然降采样使得图像的分辨率降低但是其正确匹配率显著提升。

表2 降采样图像匹配结果Tab.2 Down-sampled image matching results
4.2 低通滤波对互功率谱的影响
针对相位相关后的归一化互功率谱的傅里叶逆变换存在多个峰值,考虑到高频干扰和频谱混叠的影响,本文对两图像的互功率谱进行频域低通滤波,以抑制虚假峰值。分别采用不加窗的相位相关法、加入Rot hamming窗的相位相关法、加入Rot hamming窗并进行频域理想低通滤波处理的相位相关法,对图4的两组多谱段示例图像进行实验,结果如图5所示。两组图像正确的匹配坐标均为(30,30),图中颜色越亮表示峰值越大,表明不加窗生成的相位相关平面较加入Rot hamming窗的、加入Rot hamming窗并进行频域理想低通滤波处理生成的相位相关平面存在更多分布较为的均匀峰值干扰。而对加窗的相位相关进行频域理想低通滤波(ILPF)后,虚假峰值有了进一步的减少。
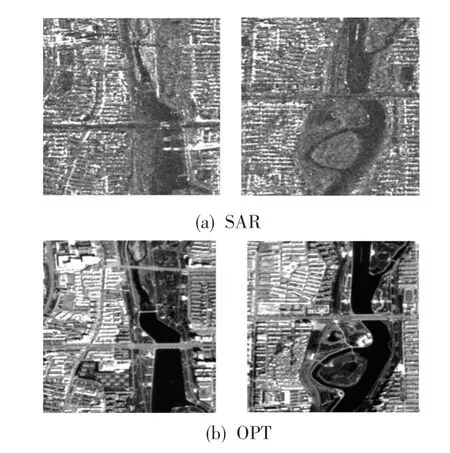
图4 示例图片Fig.4 Sample image

图5 相位相关平面Fig.5 Phase correlation plane
对加Rot hamming窗使用不同截止频率的低通滤波器,结果如图6所示,在等于1.4时可等同于没有加入低通滤波器匹配率为63%;大概在0.7时取得极值点,此时具有最佳匹配率75%;随着增大匹配率下降。综上可知,对加窗后的相位相关进行频域低通滤波可进一步提高图像匹配率。

图6 截止频率对匹配率影响Fig.6 Effect of cutoff frequency on matching rate
5 结束语
本文在基本相位相关的基础上,加入窗函数,通过增量型核回归的方法构造二维圆对称窗函数,并将其用于多谱段图像匹配。实验结果说明加窗的相位相关对多谱段图像匹配的有效性,并证明增量型核回归的方法构造二维圆对称窗函数的有效值。在此基础上再对加窗的相位相关进行理想低通滤波处理,进一步提高了匹配率。本文的方法能有效降低频谱泄露和边缘效应对相位相关算法的影响,从而提高多谱段图像匹配的正确率。
由于SAR图像和光学图像存在较大的差异,所以匹配率并不高,针对通过以上方法不能匹配的多谱段图像,基于特征的方法具有更鲁棒、更灵活的特点,未来希望通过基于特征的算法进行匹配,以进一步提高匹配率。

