基于非线性相关性和复杂网络的径流相似性分区

刘 磊，高 超，王志刚，王晓艳，章四龙，陈 娜

(1. 北京师范大学珠海校区水安全研究院，广东 珠海 519087；2. 北京师范大学水科学研究院，北京 100875；3. 北京师范大学复杂系统国际科学中心，广东 珠海 519087；4. 北京师范大学系统科学学院，北京 100875；5. 北京师范大学珠海校区政府管理学院，广东 珠海 519087)

无资料或缺测地区的水文计算问题是水文学研究的难点之一，流域分类是解决该问题的一个公认可行的方法，其依据流域气候和下垫面条件的相似性和差异性来识别水文相似流域[1-2]。通常，流域的地理特征(植被、地形等)和气候特征(降雨、蒸发等)决定着流域的水文响应行为(径流等)[3]。当不同流域的气候地理特征相似时，水文响应行为也类似，这些流域便具有一定的水文相似性。径流作为流域气候和地理特性综合作用的产物，径流相似性在一定程度上反映了流域整体的水文相似性[4]。根据水文站网中各站径流特征的相似性来实现径流相似性分区和识别径流相似河段，可为径流资料插补移用和区域洪水频率分析提供科学依据[5-6]。

水文站网是一个典型的复杂系统，在多圈层、多要素、多尺度的共同作用下，各站水文过程之间存在强烈的非线性相互作用，从而在时空上产生各种复杂形式的关联结构，表现出内在非线性、外在复杂性的特征[7]。近年来，工程水文计算领域的相关研究主要通过人为设定流域特征指标，采用相关评价方法(如聚类分析法、投影寻踪分类法、自组织映射神经网络法等)来进行相似流域分类或径流相似性分区，此类方法往往无法从系统层面准确揭示水文要素之间的内在关联机制[1，2，8-9]。复杂网络作为研究系统复杂特征的一门新兴交叉学科，在径流相似性分区研究方面提供了新的思路[10]。目前，基于复杂网络的径流相似性分区研究通常以水文站为节点、以对应径流序列之间的线性相关性大小为节点间连边是否存在的判别依据来构建水文站网的复杂网络模型，并采用社团检测算法对各站进行分级聚类。例如Halverson和Fleming[11]验证了该方法在加拿大西海岸水文站网中应用的可行性；Fang等[12]采用该方法对密西西比河流域的水文站网进行了径流相似性分区；Tumiran和Sivakumar[13]对比了美国和澳大利亚两地区水文站网的径流相似性分区结果。以上研究均依据对应径流序列间的线性相关系数(如皮尔逊相关系数)是否大于给定阈值来判定节点间连边是否存在，然而实际上不同径流序列之间往往存在着非线性相关关系[14]，不考虑它们之间的非线性相关性容易导致径流相似性分区结果不准确。

针对以上问题，本文引入Copula熵方法估算基于互信息的R统计量来度量各径流序列间的非线性相关性，基于复杂网络理论构建以水文站为节点、以对应径流序列间的R统计量大于给定阈值作为节点间连边存在依据的径流相似性分区模型，采用基于边介数的社团检测算法(GN算法)对鄱阳湖水系的水文站网进行径流相似性分区，对比最优分区结果与K均值聚类分区结果，探究复杂网络方法在径流相似性分区应用上的可行性与合理性。

1 研究区域与研究方法

1.1 研究区域

本文以鄱阳湖水系的水文站网为研究对象(图1)。鄱阳湖水系由赣江、抚河、信江、饶河、修水等5条大河和环湖直接入湖河流及鄱阳湖共同组成，其中，北部以平原、水域为主，南部以丘陵、山地为主。本文选用水文站网中44个站点的日径流序列进行研究，起止日期为2015年1月1日至2016年9月30日。

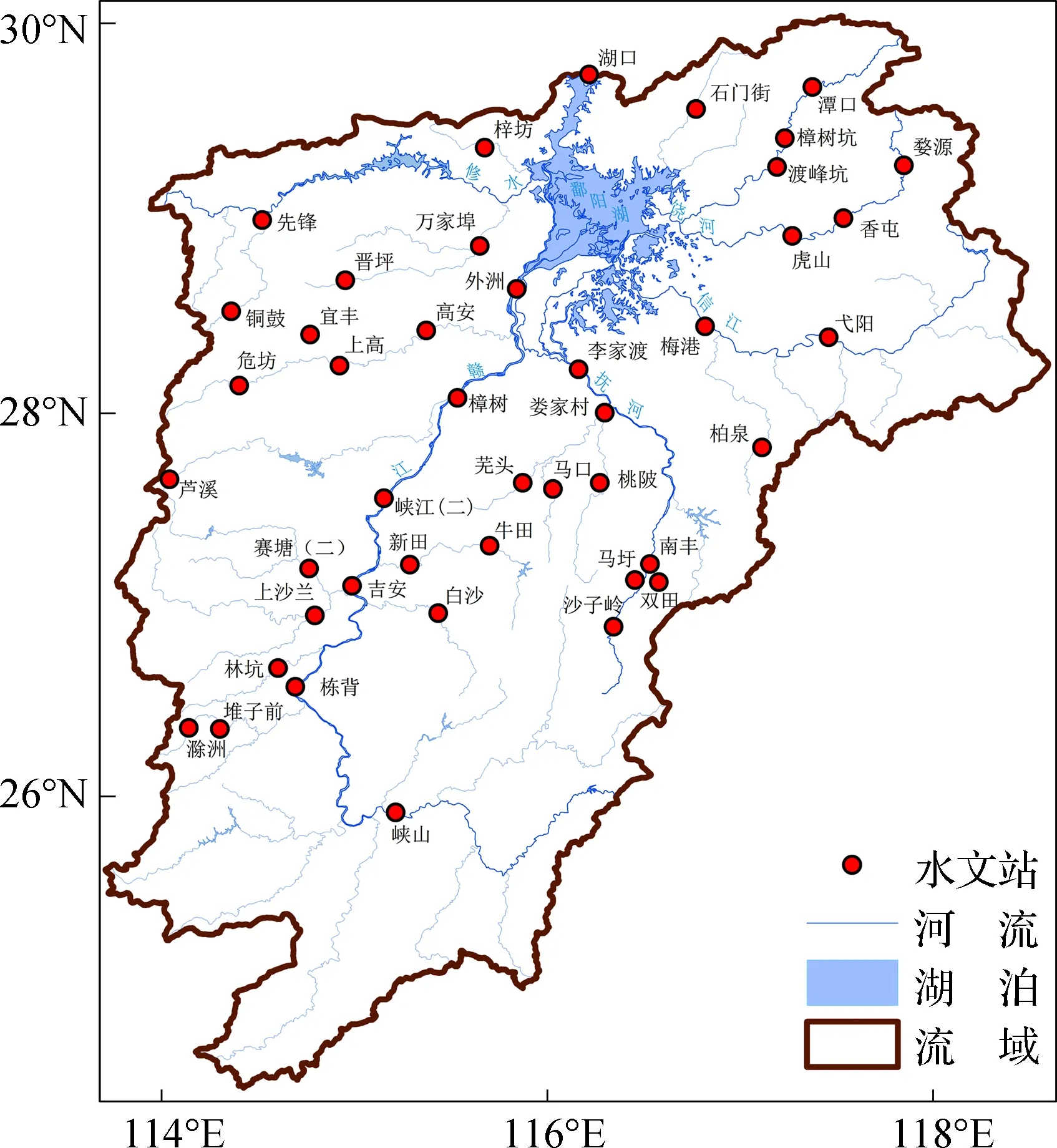
图1 鄱阳湖水系的水文站网Fig.1 Location of hydrometric network in the Poyang Lake basin

1.2 非线性相关性理论

信息熵是随机变量不确定性的度量，在水文站网中可用于量化径流序列所包含的信息[15]。假设某径流序列用连续随机变量X表示，其概率密度函数为f(x)，则X的信息熵为

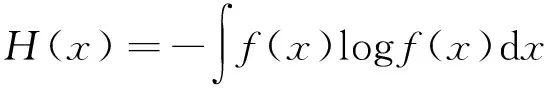
(1)

互信息是指2个随机变量之间的关联程度[16]，可用于测度2个径流序列之间的非线性相关性。假设2个径流序列分别用连续随机变量X和Y表示，FX(x)和FY(y)分别为X和Y的边缘分布函数，FX，Y(x，y)为X和Y的联合分布函数，fX(x)、fY(y)、fX，Y(x，y)分别为FX(x)、FY(y)、FX，Y(x，y)对应的概率密度函数，则X和Y的互信息I(X，Y)定义为

(2)

基于互信息I(X，Y)定义的R统计量R(X，Y)为

(3)

由上式可知，随着相关性的增加，互信息增长的速度高于R统计量，当互信息趋近于无穷大时，R统计量趋近于1。与线性相关系数相比，R统计量可度量非线性、非正态随机变量之间的相关性[17]。R统计量一般大于等于线性相关系数，当R统计量比线性相关系数大很多时，说明变量间存在明显的非线性相关性[18]。

因互信息通常很难被准确估计，Ma和Sun[19]在2008年提出了Copula熵的概念，并证明了变量间的互信息等价于其Copula熵的负值。在介绍Copula熵前，首先引入二元Copula函数：Sklar定理[20]指出若FX，Y(x,y)是连续边缘分布函数FX(x)和FY(y)的二元联合分布函数，则存在唯一的Copula函数C(u,v)，有：

FX，Y(x，y)=C(u，v)

(4)

式中：u=FX(x)和v=FY(y)分别为X和Y的边缘分布函数。设c(u，v)为C(u,v)的概率密度函数，参照式(1) ，定义X和Y的Copula熵HC(X，Y)为

HC(X，Y)=-∬c(u，v)logc(u，v)dudv

(5)

基于互信息与Copula熵负值的等价性，Ma[21]进一步提出了一种互信息非参数估计方法，本文采用该方法估算X和Y之间的非线性相关性，步骤如下：

(1) 通过顺序统计量估计X和Y的经验Copula函数。X和Y的经验Copula函数定义为

(6)

式中：n为样本长度，s表示样本(x，y)中同时满足x≤xi，y≤yj的数目，xi和yj(1≤i，j≤n)为顺序统计量。

(2) 基于X和Y的经验Copula函数，利用经典k近邻法估计Copula熵HC(X，Y)。在X和Y样本(x，y)组成的二维实数空间中，假设有n个样本点p1，p2，…，pn，计算样本点pi与其他样本点之间的最大范数距离并排序，得到顺序统计量：

z1≤z2≤…≤zn-1

(7)

式中：z1表示最近的点到pi的距离，z2表示第二近的点到pi的距离，以此类推，最近的k个点到pi的距离不超过zk，这些点称为pi的k个近邻。采用经典k近邻法估计Copula熵的公式[22]如下：

(8)

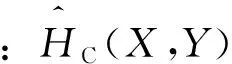
1.3 径流相似性分区方法

1.3.1 径流相似性分区模型

应用复杂网络理论将鄱阳湖水系的水文站网概化为径流相似性分区模型G=(V，E)，其中，将各站抽象为模型G的节点，节点集合记为V=(v1，v2，…，vN)；将对应径流序列X和Y之间的R统计量R(X，Y)是否大于给定阈值T作为判别节点vi与vj间连边eij是否存在的依据，边集合记为E={eij|vi，vj∈V∩R(X，Y)>T}。考虑线性相关系数的统计意义和合理性，现有研究多将线性相关系数阈值定在0.60～0.80的取值区间[13-15]，由于R统计量一般大于等于线性相关系数，本文将R统计量阈值T定在0.70～0.85的取值区间。模型G构建后，借助概率统计的思想定义某些指标来定量描述模型G的拓扑性质，常见指标包括度、平均路径长度、聚类系数、介数等[11]。

(1) 度。节点vi的度di表示与vi直接相连的其他节点的数目，这di个节点组成vi的邻接节点。节点的度描述该节点的影响力，在一定程度上反映单站在水文站网中的重要性。模型G中所有节点的度的平均值记为平均度〈d〉，有：

(9)

式中，N为节点总数，本研究中N为44。邻接矩阵是存放节点连接关系的二维数组，描述节点与节点之间的邻接关系。模型G可用邻接矩阵A=(aij)N×N表示，如果vi是vj的邻接节点，则aij=1，否则aij=0。

(2) 平均路径长度。节点vi和vj之间的最短路径是指连接这2个节点的边数最少的路径，它们之间的距离lij定义为该最短路径上的边数，若vi和vj之间不存在连通的路径，则lij→∞。平均路径长度L定义为模型G中存在连通路径的所有节点对之间距离的平均值，即：

(10)

模型G的平均路径长度越小，意味着任意2个站之间的最短路径存在更少连边，它们的联系越紧密，即认为模型G效率越高。

(3) 聚类系数。节点vi的聚类系数ci表示模型G中vi与其他节点之间的聚集程度，计算公式如下：

(11)

式中：Ei和di(di-1)/2分别表示vi的di个邻接节点之间实际存在的边数和可能存在的最大边数。单站的聚类系数越大，说明该站与其他站点之间的联系越多。模型G的聚类系数C定义为模型G中所有节点的聚类系数的平均值，表示如下：

(12)

构建与模型G具有相同节点数和边数的随机网络模型，比较2个模型聚类系数的大小，如果前者比后者大很多，则认为模型G的稳定性较高，即使移除少数站点模型G仍能保持较好的完整性。

(4) 介数。介数分为节点介数和边介数，反映相应的节点或边在整个模型中的作用和影响力，其中边介数定义为模型G中所有最短路径中经过该边的路径数目占最短路径总数的比例。

1.3.2 GN算法

许多实际网络都具有较为明显的社团结构，即社团内部节点之间的连接较为紧密，不同社团节点之间的连接相对稀疏。在模型G中，社团对应于径流特征相似的水文站集合，而各站径流特征的相似性由对应径流序列之间的R统计量来描述。分级聚类是寻找社团结构的一类传统算法，其基于各节点间连接的相似性或者强度，把网络自然地划分为各个子群。GN算法是一种经典的分级聚类算法，其原理是计算所有边介数并不断移除边介数最大的边，重复该过程直至所有边被移除[24]。GN算法以模块度作为衡量社区划分质量的指标，利用模块度局部峰值来检测最优分区效果。其中，模块度D定义为模型G在社团内部边数的比例减去随机情况下社团内部期望边数的比例[25]，计算公式如下：

(13)

式中：M表示模型G的连边总数；Oi与Oj分别表示vi与vj所属的社团，如果vi与vj同属一个社团，δ(Oi，Oj)=1，否则δ(Oi，Oj)=0。

1.3.3K均值聚类算法

K均值聚类算法是常用的无监督聚类算法，依据样本之间的距离表征样本间的相似性，采用迭代求解的方式将样本划入k个指定数目的类[26]。本文采用K均值聚类算法将水文站网分成k个径流特征相似区，主要过程为：首先将各径流序列样本标准化，计算各样本之间的欧式距离，根据最小类内方差准则确定最佳聚类数k；然后随机选取k个样本作为初始聚类中心，根据最近距离准则将样本归入各聚类中心所在的类，以此作为初始分类结果；再以各类的样本均值作为新的聚类中心，不断重复以上聚类过程，直至相邻2次的聚类中心不再变化，即为最终的分类结果。

2 结果及分析

2.1 非线性相关性

计算水文站网中各站径流序列之间的线性相关系数和R统计量，相关矩阵如图2所示。由图2可知，各径流序列之间的线性相关系数普遍小于其对应的R统计量，说明它们之间除了线性相关关系之外，还存在着一定的非线性相关关系，R统计量有效捕捉了径流序列之间的非线性相关性。

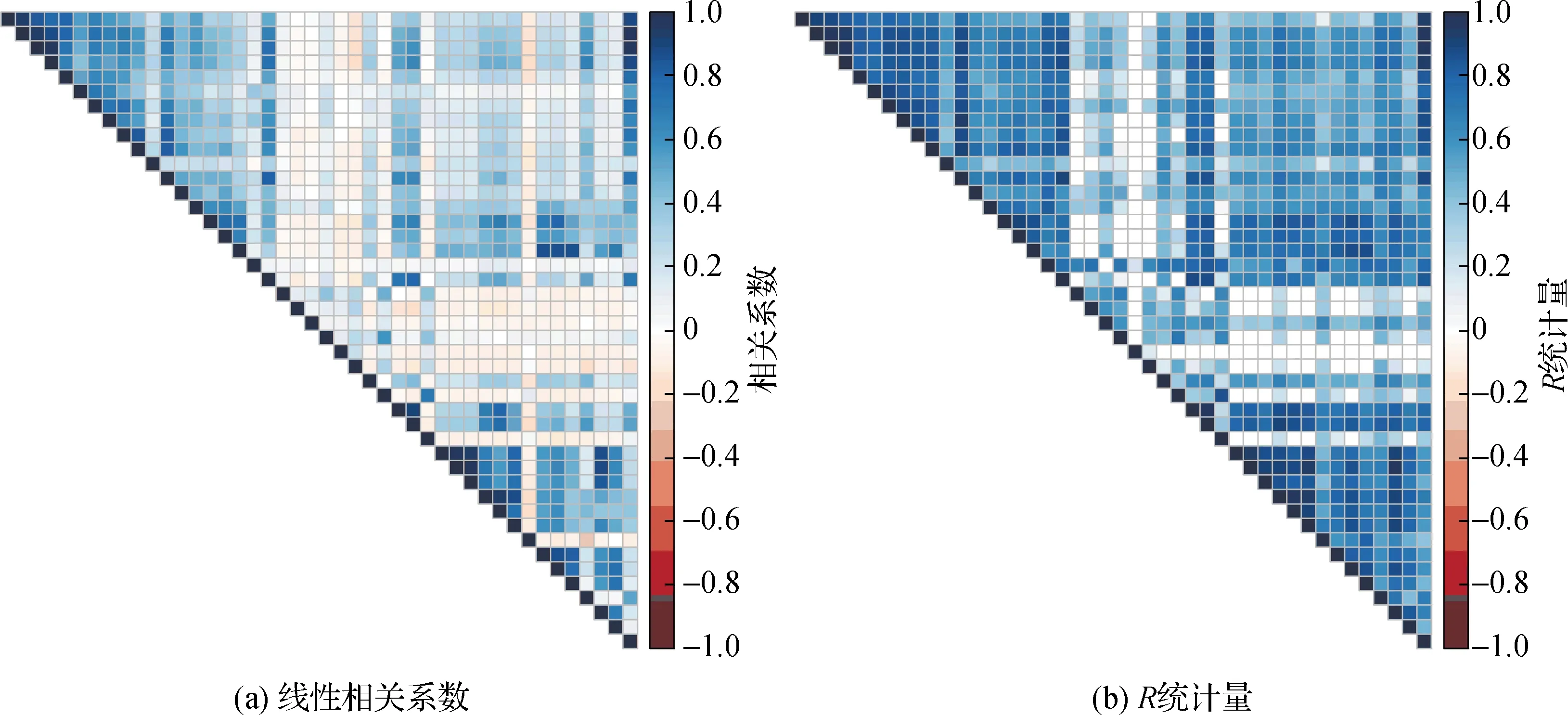
图2 不同径流序列之间线性相关系数和R统计量的相关矩阵Fig.2 Correlation matrixes of linear correlation coefficients and R statistics between different streamflow series

2.2 径流相似性分区模型

在取值区间内选取4个不同等级的R统计量阈值(T=0.70、T=0.75、T=0.80、T=0.85)，分别构建径流相似性分区模型，并统计对应模型的边数、平均度、平均路径长度和聚类系数等指标，结果见表1。由表1可知，随着R统计量阈值的增加，对应模型的边数逐渐减少，平均度和聚类系数均呈下降趋势，平均路径长度逐渐增加，这表明模型结构逐渐离散化、碎片化。相比于随机网络模型，径流相似性分区模型的平均路径长度稍小，而聚类系数很大，说明该模型表现出高效率和稳定性，取值区间内的不同R统计量阈值对模型结构影响较小。

表1 基于不同R统计量阈值的径流相似性分区模型和随机网络模型的拓扑性质

2.3 径流相似性分区

4个R统计量阈值(T=0.70、T=0.75、T=0.80、T=0.85)的径流相似性分区结果见图3，其中分区类别按站点数目由多到少的顺序依次编号，图3(a)—图3(d)的分区结果均采用同一色带标注。图3显示1类分区和2类分区包含水文站网中的多数站点，定义为大类分区；其余分区包含少数或单一站点，定义为小类分区。大类分区站点多分布于大河干流或者支流下游，集水面积相对较大，往往包含一定面积比重的冲积平原。小类分区站点往往位于河流的源头，山丘区分布较为广泛，集水面积相对较小。不同河流水系的源头之间水文气候、地形地貌等特征差异较大，故对应站点多属不同小类分区。此外，抚河流域上中游分布着较多小类分区站点，虽然其水文气候和地形地貌特征相近，但集水面积相对较小且受湖库调蓄作用影响较大，导致这些站点的径流特征互不相似，从而各自形成小类分区。

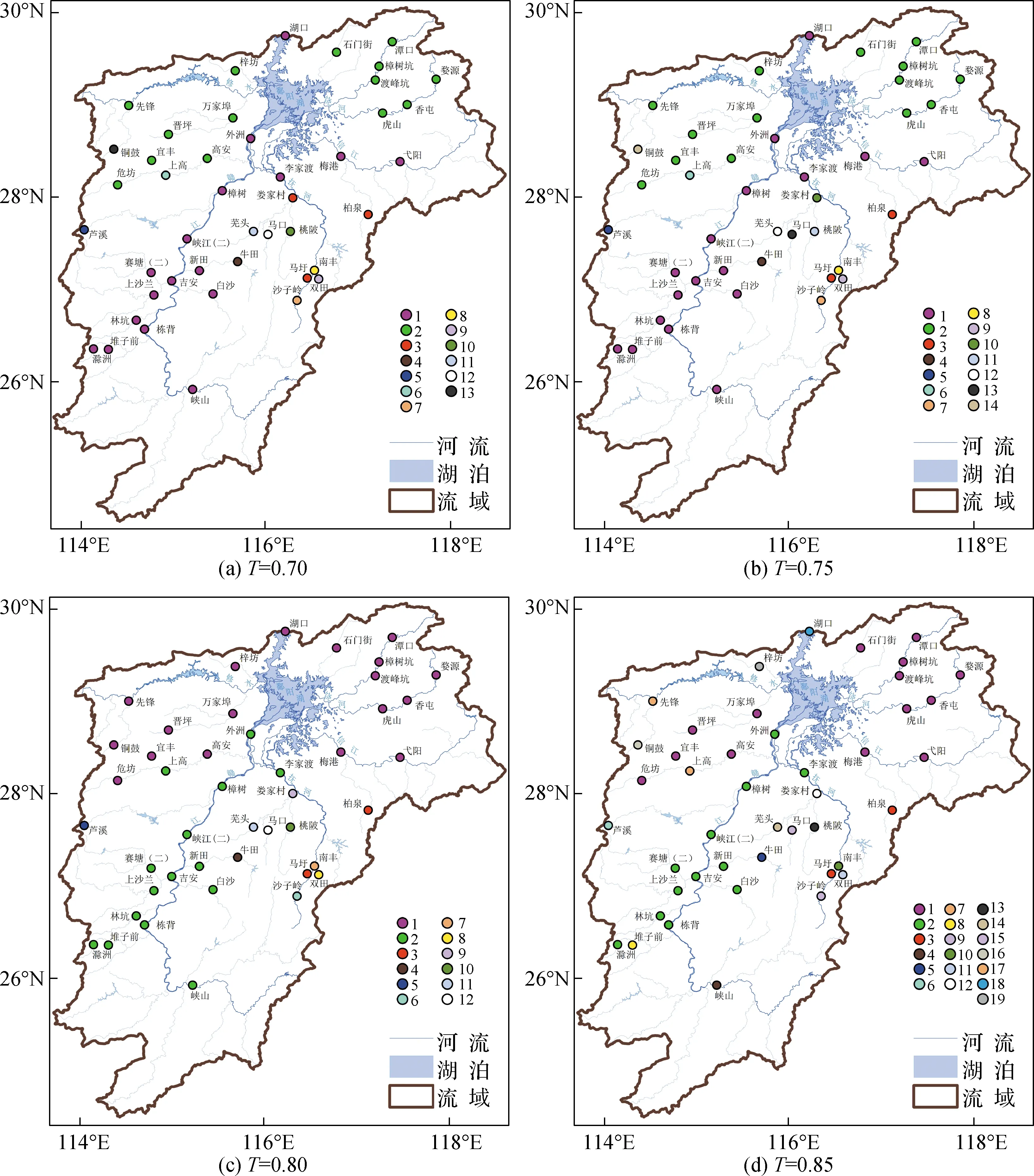
图3 基于不同R统计量阈值的径流相似性分区结果Fig.3 Streamflow similarity regionalization results under different R-statistic thresholds

依据不同站点所属的大类分区来识别径流相似河段。对于同一大河，其上下游之间具有较为清晰的水力联系，径流特征较为相似，干流站点同属一个大类分区，它们所处的河段识别为径流相似河段。如赣江干流的栋背、吉安、峡江(二)、樟树、外洲等站点所处的河段为径流相似河段。对于不同大河，也有不同站点同属一个大类分区，如不同R统计量阈值下，抚河下游干流的李家渡站始终与赣江干流的站点同属一个大类分区，因此该站所处的抚河下游干流和赣江干流为径流相似河段。

根据2个大类分区的空间差异性，可将水文站网大致分为南北两部分。随着R统计量阈值的增加，南北部范围内大类分区的编号和范围有所变化。T=0.70或T=0.75时，信江的梅港站和弋阳站同属南部大类分区；而T=0.80或T=0.85时，它们改属北部大类分区，导致南部大类分区站点的数目少于北部大类分区站点的数目，使得各自所属大类分区的类别发生调换。这是由于两站与南部大类分区站点之间的R统计量相对较小且连边较多。它们与南部大类分区站点的连边随着R统计量阈值的增加而减少得更多，而与北部大类分区站点的连接变得相对更为紧密，从而导致其所属大类分区的范围由南部变为北部。此外，位于鄱阳湖入江口的湖口站也类似，所属分区的类别也随着R统计量阈值的增加发生变化：当T=0.70或T=0.75时，湖口站属于南部大类分区；当T=0.80时，湖口站改属北部大类分区；当T=0.85时，湖口站则自成小类分区。R统计量结果显示湖口站与梅港站之间的R统计量最高(0.82)，与梅港站类似，湖口站与南北两部站点的连边随着R统计量阈值增加而逐渐减少，当连边减少至一定程度时，湖口站便自行形成小类分区。

表2统计了4个R统计量阈值(T=0.70、T=0.75、T=0.80、T=0.85)的径流相似性分区结果中各类分区站点的数量。随着R统计量阈值的增加，分区总数依次为13、14、12和19，其中1类和2类分区站点的占比分别为70.5%、70.5%、75.0%和59.1%。T=0.70或T=0.75时，径流相似性分区模型中的连边较为紧密，径流序列相关性较弱的两站可能划为同类分区，分区结果无法完全区分径流特征的差异性；T=0.85时，模型中的连边变得稀疏，模型结构过于离散，形成的小类分区过多，分区结果无法有效识别径流特征的相似性，故分区效果不佳；T=0.80时的径流相似性分区结果最优，此时水文站网划分为南北2部分共12类分区，其中，北部仅含1类分区，南部含2类分区以及所有小类分区。此时，修水、饶河和信江干支流的站点同属1类分区，以上大河的干支流为径流相似河段；而赣江干流的站点与抚河下游干流的李家渡站同属2类分区，说明抚河下游干流与赣江干流为径流相似河段。

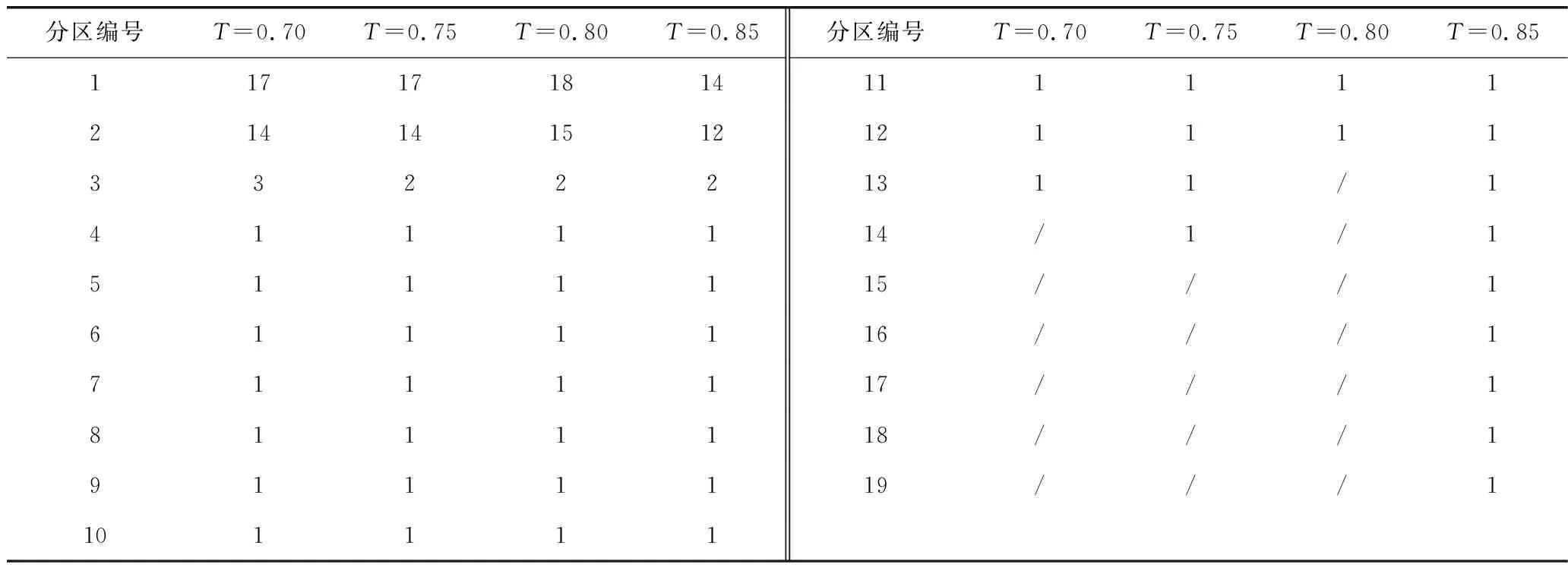
表2 基于不同R统计量阈值的径流相似性分区结果的水文站数量

2.4 分区结果评价

对比T=0.80时的径流相似性分区结果与K均值聚类算法分区结果(见图4)，以检验径流相似性分区结果的合理性与可行性。图4(a)表明K均值聚类算法分区结果中站点所属分区的类别与其集水面积密切相关，如分布于大河上游或支流、集水面积较小的站点同属一类分区，而位于鄱阳湖入江口、集水面积最大的湖口站则自成一类分区。此外，K均值聚类方法将抚河流域上中游站点划入同一分区，未能有效捕捉到湖库对径流的调节作用。这是因为K均值聚类方法将不同径流序列间的欧式距离作为衡量其径流相似性的指标，主要描述的是径流量级的绝对差异，往往更可能将径流量级相近的站点划入同类分区；而复杂网络方法以不同径流序列间的非线性相关性作为度量其相似性的标准，更多的是从动态变化特征上区分差异。抚河流域上中游站点的径流量级相近，但受湖库调蓄影响，径流的动态变化特征差异较大。因此，相较于K均值聚类算法，本文复杂网络方法可有效捕捉到湖库对径流的调节作用，从而准确识别水文站网中各站径流特征的相似性和差异性，其分区结果更为合理。

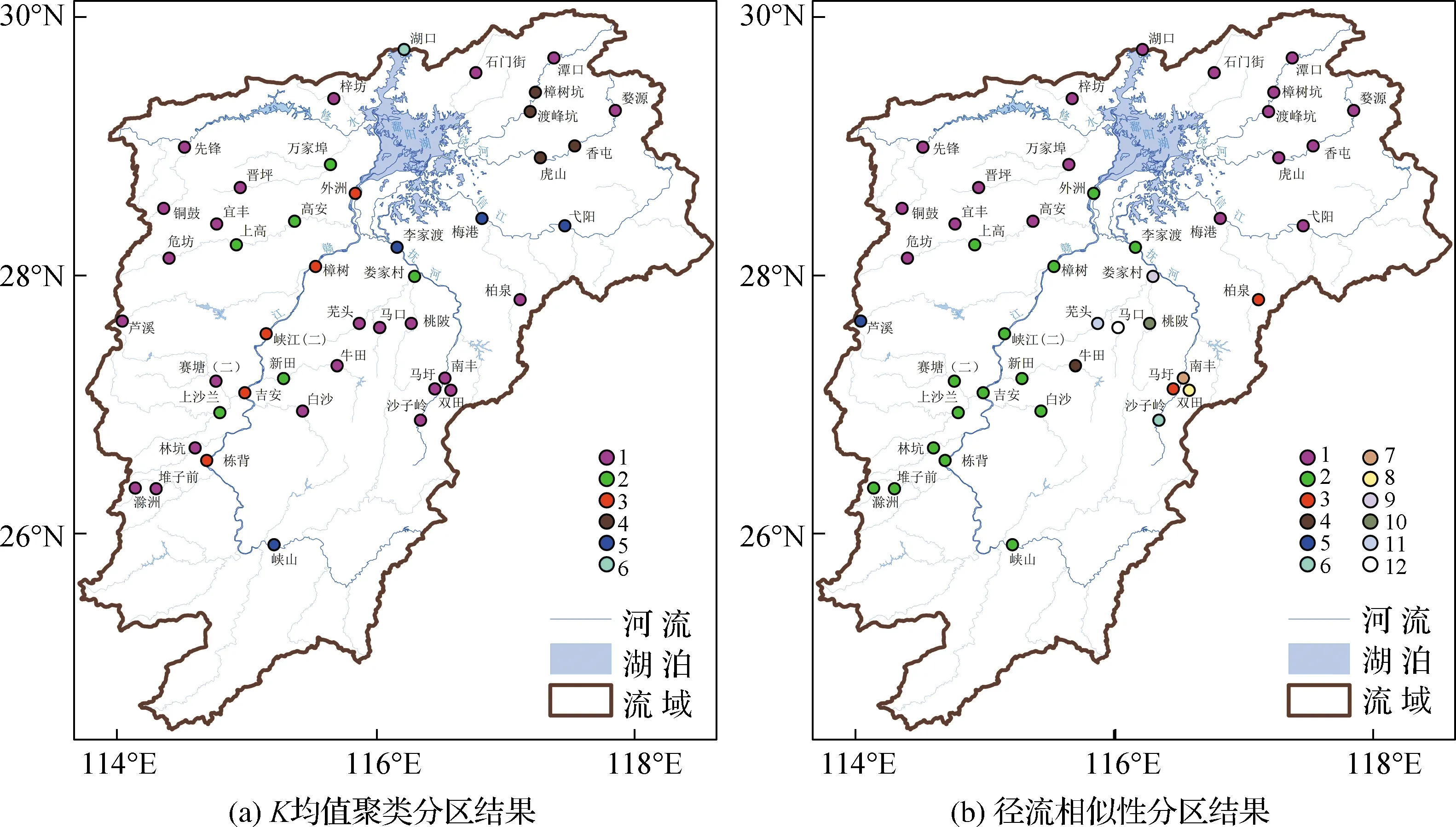
图4 K均值聚类分区结果与径流相似性分区结果对比Fig.4 Comparison of K-means clustering regionalization results and streamflow similarity regionalization results

3 结 论

本文以鄱阳湖水系的水文站网为研究对象，采用Copula熵度量径流序列间非线性相关性的R统计量，以此为连边存在依据构建了基于复杂网络的径流相似性分区模型。采用GN算法对模型进行了径流相似性分区，并与K均值聚类方法对比，验证了复杂网络在径流相似性分区应用上的可行性和合理性。主要结论如下：

(1) 相比线性相关系数，R统计量更适用于度量各径流序列间的非线性相关性。

(2) 基于复杂网络的径流相似性分区模型具有高稳定性和高效率性，对取值区间内的R统计量阈值变化不敏感。

(3)R统计量阈值为0.80时，径流相似性分区结果最优，此时水文站网划分为南北两部分共12类分区，其中，北部含1类分区，南部含2类分区以及所有小类分区。修水、饶河和信江干支流为径流相似河段，而抚河下游干流与赣江干流为径流相似河段。

(4) 相比K均值聚类分区结果，R统计量阈值为0.80时的复杂网络径流相似性分区结果更为合理。