考虑自重影响的拓扑优化方法

宋英杰 吴超 尹书翰 黄俊斌 宋勇宏

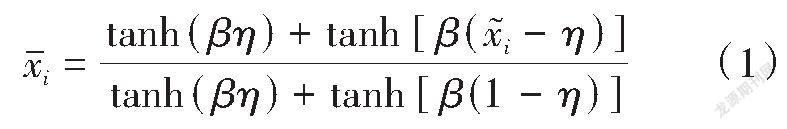
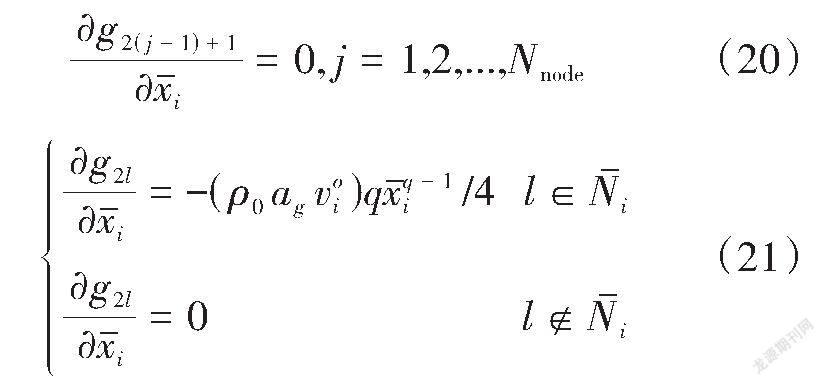
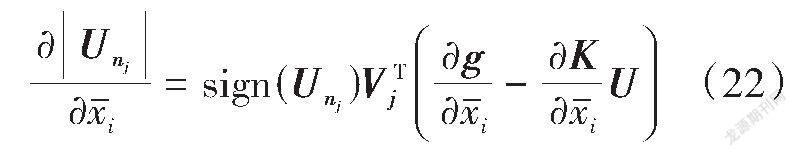
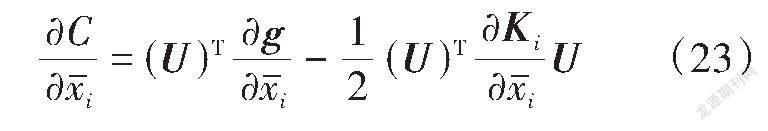
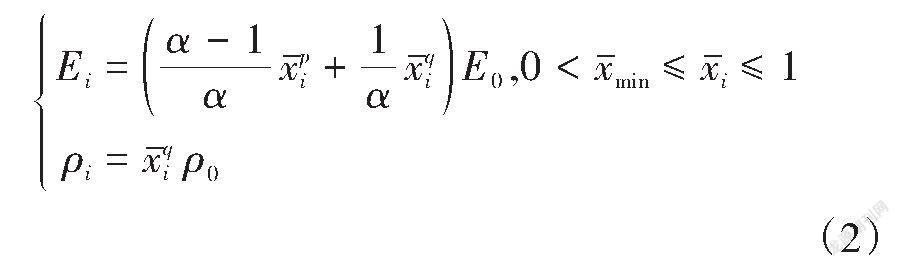
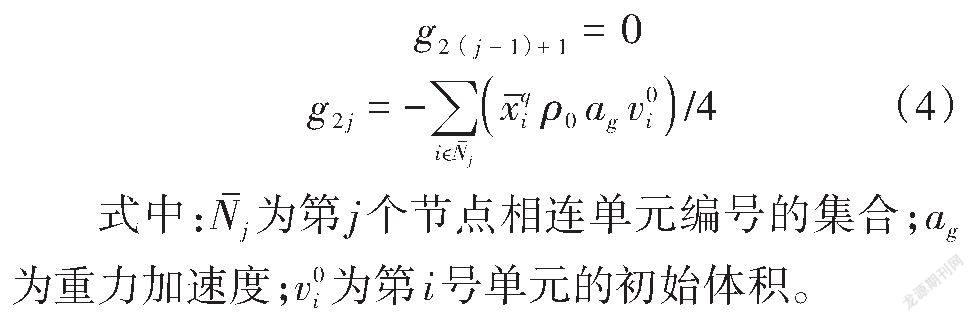
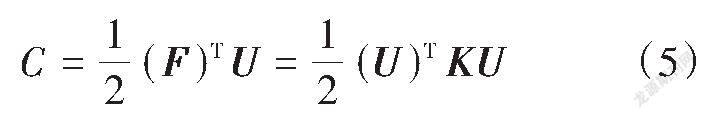
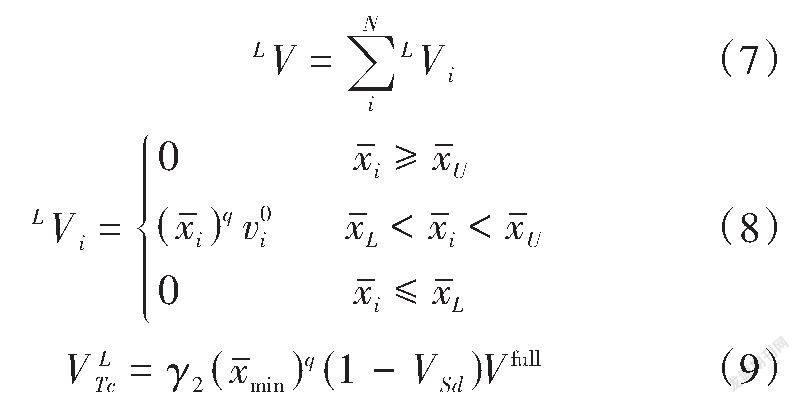
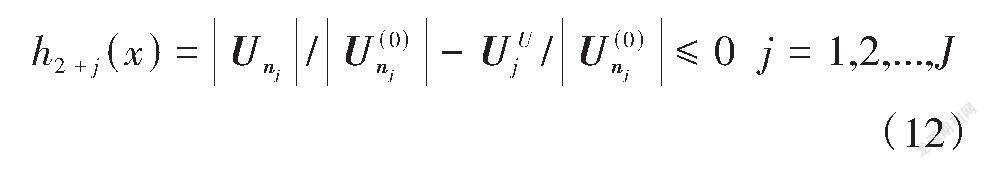
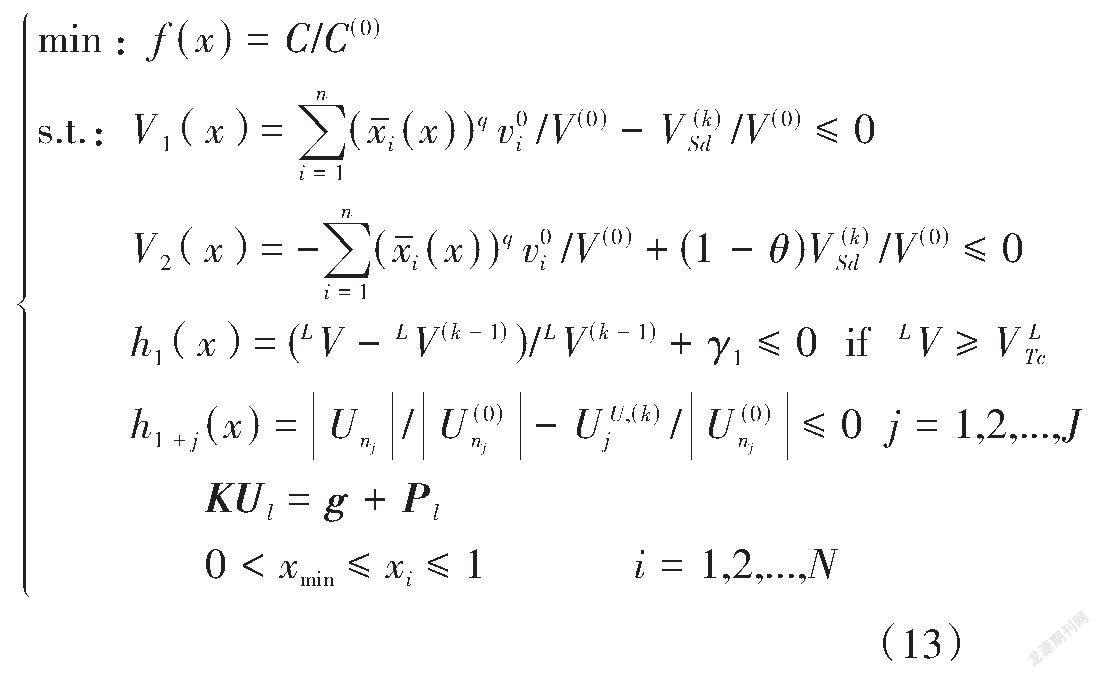
摘 要：针对在考虑自重影响的连续体结构拓扑优化中常见的问题，本研究提出一种新的拓扑优化方法。首先，为避免寄生效应，提出一种带惩罚的固体各向同性材料（SIMP）改进模型，建立刚度模量、质量密度和体积光滑惩罚函数三者间的合理匹配关系。同时，引入密度过滤、Heaviside映射的三场过滤方案，并提出一种低物理密度单元的体积变化率约束措施，从而极大地提高考虑自重效应的结构拓扑问题的优化计算效率，获得清晰的0-1分布。基于上述方法，建立以结构柔顺度最小为目标，同时考虑变体限约束、位移约束以及低物理密度单元的体积变化率约束等措施的优化模型。最后，采用MMA算法对优化模型进行求解，并通过算例验证本研究所提出的方法是正确有效的。

关键词：拓扑优化;连续体结构;结构自重;低密度约束

中图分类号：TH122     文献标志码：A     文章编号：1003-5168（2022）12-0030-06

DOI：10.19968/j.cnki.hnkj.1003-5168.2022.12.006

A Topology Optimization Method Considering the Effect of Self-Weight

SONG Yingjie    WU Chao    YIN Shuhan    HUANG Junbin    SONG Yonghong

（School of Automotive and Mechanical Engineering，Changsha University of Science and Technology，Changsha 410014，China）

Abstract：Aiming at the common problems in topology optimization of continuum structures considering the influence of self-weight，this paper proposes a new topology optimization design method.First，to avoid parasitic effects， an improved Solid Isotropic Material with Penalty （SIMP） model is proposed，which establishes a reasonable matching relationship between stiffness modulus and bulk smoothness penalty function.At the same time，a three-field filtering scheme of density filtering and Heaviside mapping is introduced，and a volume change rate constraint measure for low physical density cells is proposed to greatly improve the optimization calculation efficiency of structural topology problems considering self-weight effects，and obtain clear 0-1 distributionBased on the above method，an optimization model is established，which takes the minimum structural compliance as the goal，and considers the constraints of the variation limit and the volume change rate of the low physical density element.Finally，the MMA algorithm is used to solve the optimization model.And the method proposed in this paper is verified to be correct and effective by an example.

Keywords：topology optimization;continuum structure;self-weight;low density constraint

0 引言

當今新一轮工业革命方兴未艾，而其核心驱动力便是智能制造[1]。智能制造技术的发展不仅要使设计出的结构具有高性能和轻量化的特点，还要考虑实际工程应用中结构自重的影响。虽然拓扑优化法在工程机械、航空航天、车辆船舶及建筑土木等领域获得成功应用，但在早期的拓扑优化过程中，往往忽略了包括自重载荷、热载荷、旋转部件的离心载荷和惯性加速度载荷在内的体积力。

Rozvany等率先开展了基于自重的拓扑优化问题研究。Bruyneel等发现，对体积力在内的载荷结构进行拓扑优化时存在3个问题：①在优化过程中，柔顺度目标函数不是单调函数;②优化结果的体积不受约束;③低密度区域有寄生效应[2]。近年来，虽然有学者针对上述问题进行了研究，但却始终无法避免优化过程中的低物理密度单元对结构的影响，且整个优化过程收敛较为缓慢，直接使用固体各向同性材料惩罚模型（SIMP）并不能解决这些问题。

基于此，本研究结合各种拓扑优化方法及相关领域的最新研究进展，提出一种改进的SIMP插值方法，可有效解决考虑结构自重时所带来的问题。本研究还提出了低密度单元体积变化率的约束方法，在进一步避免寄生效应的同时，既降低了优化过程中低密度单元对结构的影响，获得清晰的0-1分布，又极大地提高了计算效率。

1 过滤方法和材料惩罚模型

1.1 过滤方法

为建立连续体结构的有限元模型和拓扑优化模型，本研究先将优化结构设计域离散为[N]个四节点的四边形单元，并为设计域中的每个单元分配一个设计变量[xi]。通过密度过滤技术[3]和Heaviside映射函数[4]来形成由设计变量[xi]、中间变量[xi]、物理变量[xi]组成的三场过滤方案，既可避免拓扑优化过程中出现棋盘格现象，又能解决灰度单元问题。Heaviside映射函数见式（1）。

式中：[β]是Heaviside映射函数的曲率参数，本研究所有算例中[β]的初始值均为10-5，并按照[β（m）=max（1，2 β（m-1））]每50迭代步更新一次（即每50个外循环迭代步m增加1）;本研究中[η]取值为0.04。

1.2 改进的材料惩罚模型

SIMP法是现有拓扑优化方法中最常用的一种方法。针对考虑自重影响的拓扑优化问题，采用经典的SIMP模型来解决时，在低密度区域，结构刚度与其自重存在较大差异，使结构刚度难以承受自重，最终导致结构刚度不足和无界位移。本研究提出一种改进的固体各向同性惩罚材料模型，见式（2），用来解决拓扑优化中自重载荷引起的低密度区域的寄生效应，同时保证体积约束的有效性。

式中：[E0]是初始单元材料的弹性模量;[ρ0]为单元初始质量密度;[p]和[q]分别为单元的刚度模量惩罚因子和体积惩罚因子;[α]为刚度模量的多项式函数的惩罚参数。通过数值仿真研究发现，当[p=5]、[q=2]、[α=25]时，对寄生效应的抑制效果较好，且能获得较好的拓扑优化结果。

2 优化模型建立及灵敏度分析

2.1 结构自重处理和目标函数

当考虑与质量密度相关的自重时，载荷向量表达式见式（3）。

[F=g+P]      （3）

式中：[F]为载荷向量;[g]为结构自重向量;[P]为外载荷向量。

考虑平面应力问题的四节点四边形有限元和沿垂直方向施加的重力载荷，使得每个有限元四分之一的自重沿垂直方向平均分配给其四个节点，见式（4）。

式中：[Nj]为第[j]个节点相连单元编号的集合;[ag]为重力加速度;[v0i]为第[i]号单元的初始体积。

由结构刚度矩阵[K]和位移矢量[U]可以得到结构的柔顺度C，见式（5）。

2.2 低密度单元体积变化率约束措施

为抑制优化过程中低密度单元的密度变量波动，并通过提升优化过程中结构清晰度来提高计算效率，本研究提出一个低密度单元体积变化率约束，见式（6）。

[h1（x）=（LV-LV（k-1））/LV（k-1）+γ1≤0   if   LV≥VLTc]

（6）

式中：[LV]为物理密度变量在0.001～0.100的所有單元体积之和;[VLTc]为是否引入低密度单元体积变化率约束的阈值;[LV（k-1）]为第k-1迭代步[LV]值。式（7）（8）（9）给出了[LV]和[VLTc]的表达式，[γ1]为一个经验参数，本研究取值为0.05。当[LV≥VLTc]时，在后续优化模型中引入低密度单元体积变化率约束。

式中：[N]为设计域中单元的数量;[Vfull]为结构拓扑中充满材料时设计域的总体积;[γ2]为一个经验参数，本研究γ2取值为5。

为了使式（8）更易求导，引入Sigmoid函数[1/（1+e-ζx）]近似单位阶跃函数。[LVi]和[LV]的近似平滑函数见式（10）和式（11）。

2.3 位移约束

在实际工程应用中，要在保证结构刚度的前提下，还要保证结构中指定点的位移足够小。因此，本研究依据需要限制位移的自由度数量，引入一个或多个结构位移约束，见式（12）。

式中：[UUj]为优化结构中[j]点的位移约束限;[nj]为[j]点位移约束所指定的优化结构自由度编号;[Unj]为优化结构第[nj]号自由度的位移;[U（0）nj]为[Unj]在初始迭代步中的值;[J]为需要受到位移约束的自由度的个数，即位移约束的个数。

2.4 优化模型

优化结果体积不受约束是考虑设计变量相关载荷的结构拓扑优化中存在的三个问题之一[2]。为了进一步保持体积约束的有效性，本研究引入了体积上下限约束[V1（x）]和[V2（x）][5]。由于Heaviside曲率参数发生变化时会导致结构位移和柔顺度发生较大变化，故采用Rong等[5]提出的变约束限方案，来保证结构性能在拓扑优化过程中的稳定变化。综上所述，以结构柔顺度最小为目标函数，考虑结构自重影响，包含体积相关约束和位移约束的结构拓扑优化模型见式（13）。

式中：[xmin]为一个小量;[V（0）]为初始迭代时优化结构的总体积;[VSd]为优化目标体积;[θ]为体积下限松弛参数，在本研究中θ的取值为0.004;[V（k）Sd]和[UU，（k）j]分别表示在第k个迭代步中结构体积的变化约束限和优化结构的j点位移变化约束限，计算公式见式（14）至式（17）。

式中：[ζ1]和[ζ2]为经验参数，在本研究的算例中分别设定为0.01和0.04[6];[V（0）]为Heaviside曲率参数[β]变化步以及最接近k步的结构体积;[U（0）nj]为第[nj]号自由度处的位移。

2.5 灵敏度分析

本研究采用MMA算法[7]来求解，因此，需要求解优化模型式（13）中各个性能函数的灵敏度。由链式求导法则可知，结构的任意性能函数对设计变量的导数见式（18）。

由惩罚模型式（2）可得整体刚度矩阵关于物理密度变量[xi]的导数，见式（19）。

式中：[Ki]和[K0i]分别为整体坐标系下第i个单元的刚度矩阵和第i个单元的初始刚度矩阵。

与结构自重相关的等效节点力向量对物理密度变量[xi]的导数见式（20）和式（21）。

假设[Vj]为单位虚荷载作用在优化结构的第[nj]号自由度上所产生的结构位移矢量，则结构第[nj]号自由度的位移绝对值对物理密度变量[xi]的导数见式（22）。

基于式（5），优化结构柔顺度对物理密度变量[xi]的导数见式（23）。

基于优化模型（13）中的两个体积不等式约束，可求得其对物理密度变量[xi]的导数，见式（24）和式（25）。

基于式（11），可以求得其对物理密度变量[xi]的导数，见式（26）。

式（22）至式（26）是根据链式求导法则得到的位移、柔顺度和体积相关函数对设计变量的导数。

3 算例分析

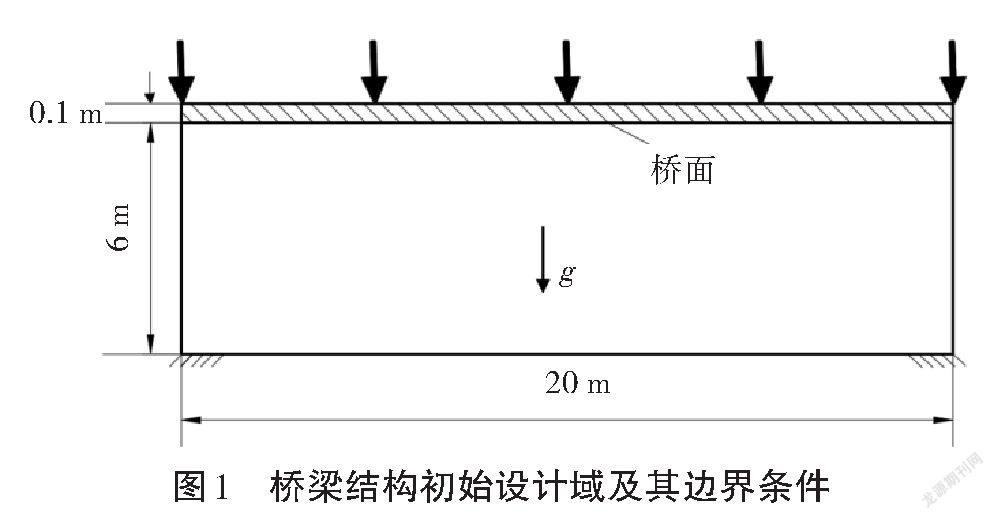
为验证本研究所提出的拓扑优化方法的准确性，针对图1所示的考虑自重载荷的桥梁结构进行优化求解。

图1所示的桥梁结构的荷载和边界条件是左右对称的。桥梁结构设计域为一个顶部加载、底部两端固定支撑的矩形区域，长为20 m、高为6.1 m、厚为0.006 7 m，即桥面为长20 m、高0.1 m、厚度0.006 7 m的非设计域。桥面上竖直向下施加大小为-7 500 N/m均布力。初始材料的弹性模量为[E=2×1011Pa]，其泊松比ν为0.3，其质量密度ρ0为7 850 kg/m3。整个设计域和非设计域全部离散为600×183=109 800个四节点矩形平面应力单元。设置密度过滤半径为[rmin=2Δ]，其中[Δ]为最大单元边长。在此示例中，目标体积与设计域初始体积的比值设定为0.5。本研究的算例在考虑自重的前提下，以柔顺度最小为目标，包含体积相关约束和位移约束等多种约束条件。其中，顶部中点垂直位移规定为小于0.003 5 m。

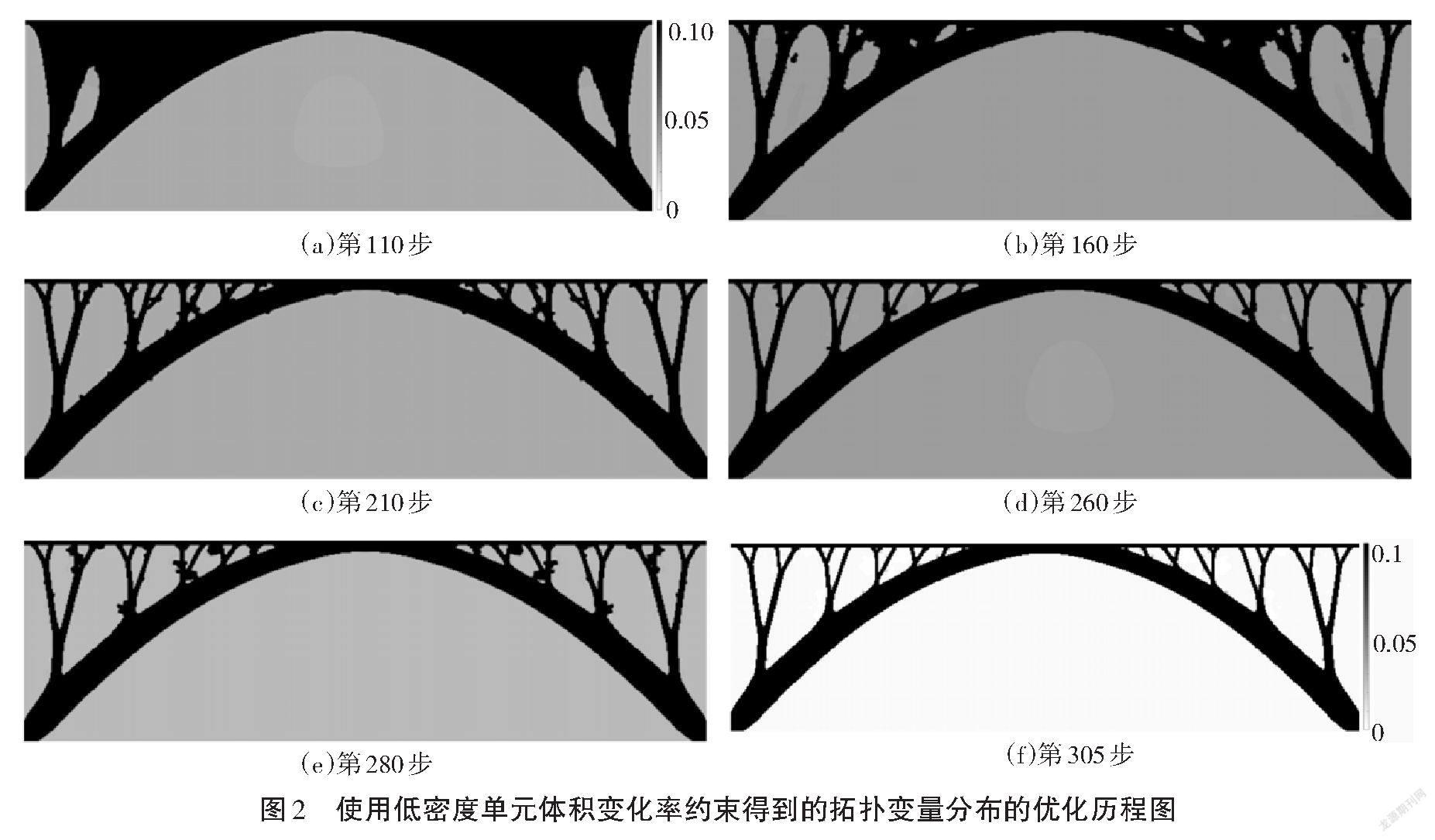
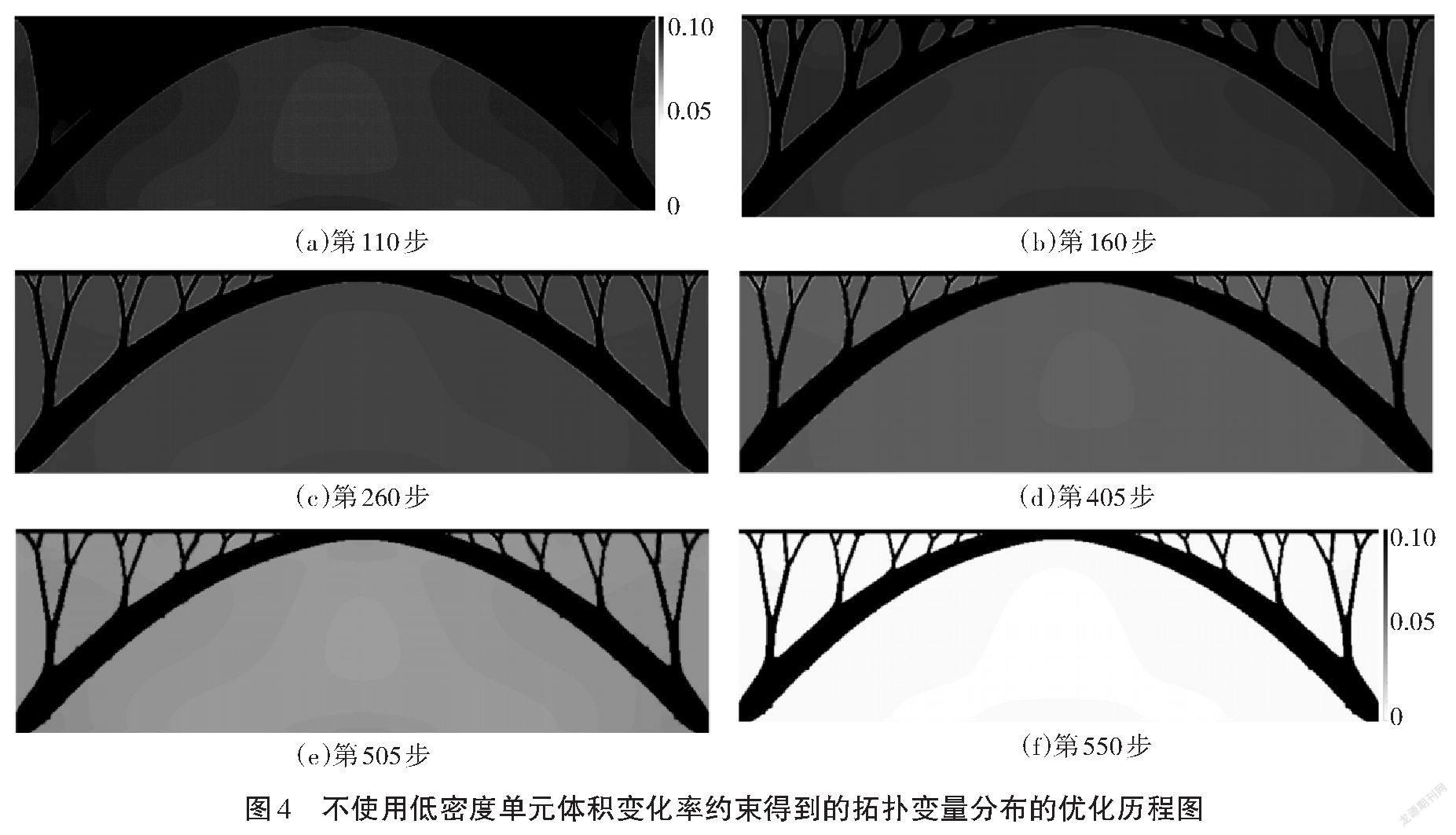
图2给出了使用本研究提出的方法得到的桥梁结构拓扑变量分布的优化历程图。其最优拓扑构型如图2（f）和图3所示，最优拓扑结构柔顺度为113.84 N·m，桥顶中点垂向位移为0.002 78 m。图4给出了在没有考虑低密度单元的体积变化率约束时得到的拓扑变量分布的优化历程图，其最优拓扑结构如图4（f）和图5所示。最优拓扑结构的柔顺度和桥顶中点垂向位移分别为114.07 N·m和0.002 79 m。与图2一样，图4中最黑的区域为物理密度变量大于或等于0.1的单元所占区域，从而突出显示物理密度变量在[0，0.1]范围内的元素分布，可以有效地对比出低密度单元体积变化率约束的作用。这些数据以及最优拓扑构型图可以充分表明本研究所提出的方法能够获得满足所有约束的最佳拓扑。

尽管图3的最优拓扑结构与图5相似，但在相同的收敛条件下，通过本研究所提出的低密度单元体积变化率约束方法，经过350步优化迭代可获得结构的最优拓扑构型图及相关参数，而不受低密度单元体积变化率约束的方法需要经过550步优化迭代才能获得最终拓扑结构。显然，使用本研究提出的低密度单元体积变化率约束可以极大地提高考虑自重影响的结构拓扑问题的优化计算效率，在本算例中对计算效率的提升高达36.3%。

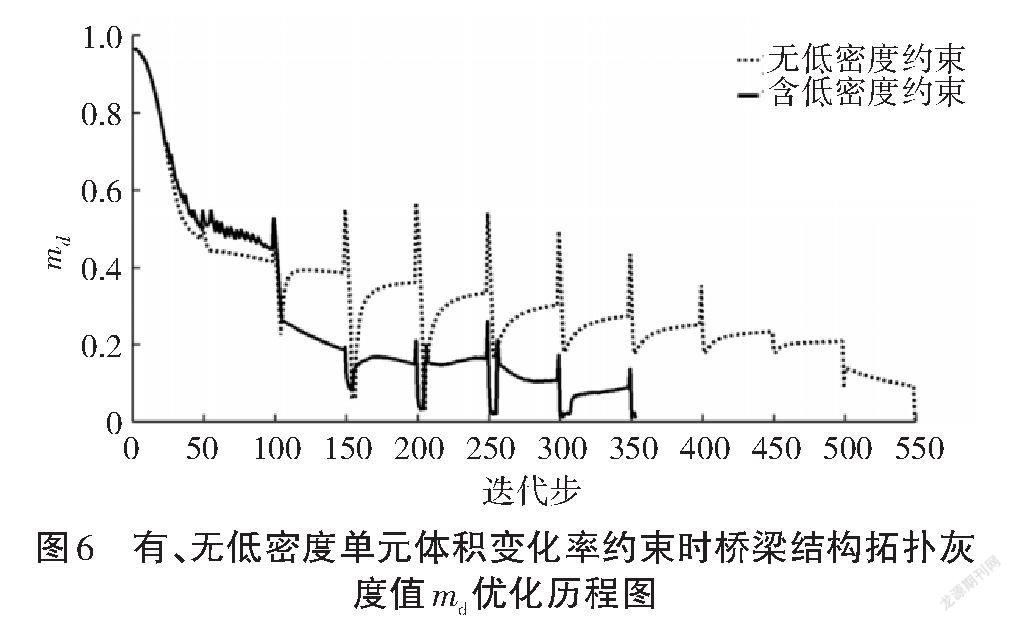
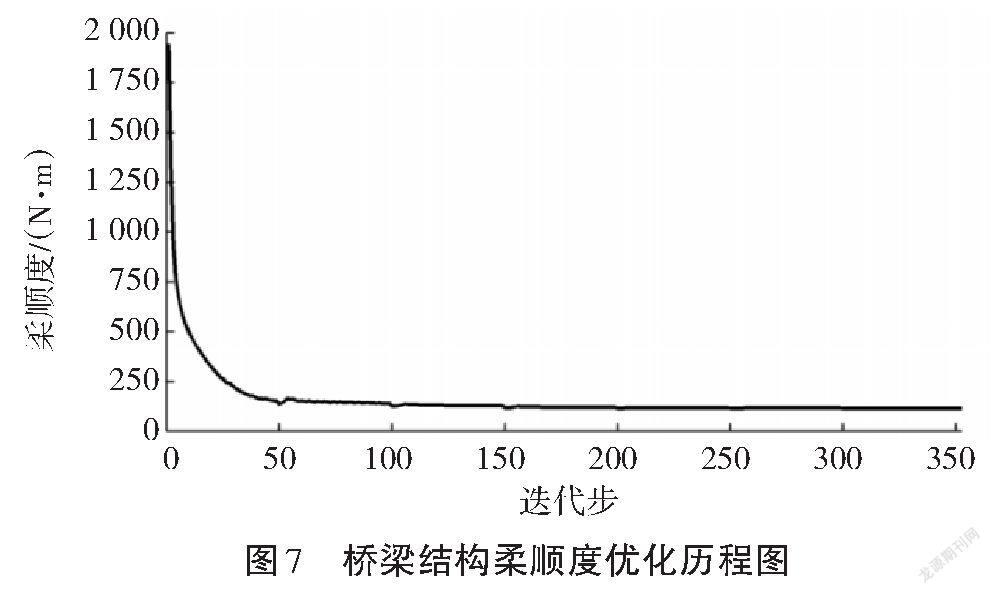
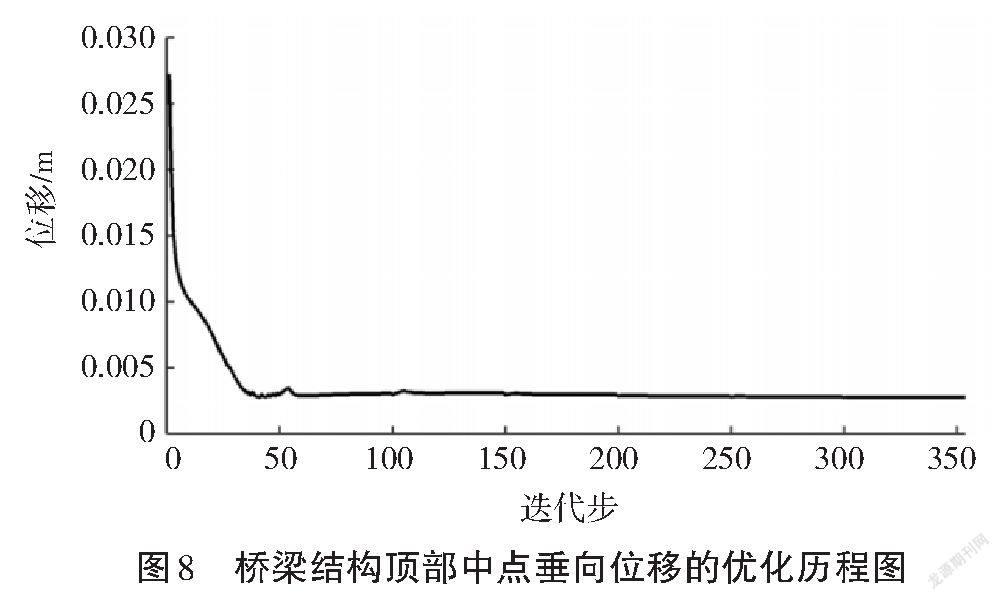
图6给出了使用该方法得到的结构拓扑灰度值md的优化历程，其中两条曲线分别代表考虑与不考虑低密度单元体积变化率约束时灰度值md的变化。由于Heaviside曲率参数的变化，图6的曲线中有一些明显的跳跃。图7为在使用本研究所提出的方法后得到的桥梁结构柔顺度优化历程。图8给出通过使用本研究提出的方法得到的桥梁顶部中点垂向位移的优化历程，其最终位移值达到了相应约束的要求。对图2至图8分析可以发现，虽然图3和图5给出了几乎相同的最优拓扑构型图，但本研究所提出的考虑低密度单元的体积变化率约束方法可以显著地抑制物理密度的波动，降低优化过程中中间密度单元对结构的影响，极大地提高拓扑优化计算效率。

4 结论

本研究基于SIMP方法，提出了一种考虑自重影响的连续体结构拓扑优化方法，并通过一些具体算例证明了所提出方法的可行性、有效性和特点，并得到以下3个结论。

①本研究所提出的改进SIMP模型可有效解决基于自重影响的拓扑优化过程中的寄生效应。

②本研究通过引入的体积上下限约束和指定点的位移约束在考虑自重的拓扑优化过程中发挥作用。

③引入的Heaviside三场过滤方案和本研究提出的一种低物理密度单元的体积变化率约束措施，可极大地提高考虑自重影响的结构拓扑问题的优化计算效率，并能得到更为清晰的0-1分布。

参考文献：

[1] 姚锡凡，景轩，张剑铭，等.走向新工业革命的智能制造[J].计算机集成制造系统，2020（9）：2299-2320.

[2] BRUYNEEL M，DUYSINX P.Note on topology optimization of continuum structures including self-weight[J].Structural and Multidisciplinary Optimization，2005（4）：245-256.

[3] BOURDIN B.Filters in topology optimization[J].International Journal for Numerical Methods in Engineering，2001（9）：2143-2158.

[4] WANG F ，LAZAROV B S，Sigmund O.On projection methods，convergence and robust formulations in topology optimization[J].Structural and Multidisciplinary Optimization，2011（6）：767-784.

[5] Rong J H，Rong X P，Peng L，et al.A new method for optimizing the topology of hinge-free and fully decoupled compliant mechanisms with multiple inputs and multiple outputs[J].International Journal for Numerical Methods in Engineering，2021（1）：2863–2890.

[6] 何一凡，趙磊.基于应力约束的框架结构拓扑优化研究[J].河南科技，2021（28）：87-93.

[7] 陈成，赵圣佞.基于Heaviside过滤和可行域调整的SIMP方法拓扑优化设计[J].河南科技，2018（34）：26-28.

[8] 李方义，卢志宏，易继军.考虑自重影响和屈曲约束的结构拓扑优化方法[J].长沙理工大学学报（自然科学版），2021（3）：97-104.