优化古典概率教学，提升学生探究能力

中国政法大学科学技术教学部 刘淑环

美国著名教育家、哲学家、心理学家约翰·杜威说过：“科学教育不仅仅是要让学生学习大量的知识，更重要的是学习科学研究的过程或方法”，在教育家施瓦布所倡导的探究教学中，他认为学习“不在于占有的信息，而在于拥有的探究能力”。

概率又称“或然率”“可能性”，是概率论课程中的基本概念。古典概率是计算事件概率的一种形式，对古典概率内涵的理解和掌握，关系到学生概率思维的养成及学习概率论其他内容的效果。本文结合教学实践，通过具体实例，对优化古典概率教学内容、激发学生学习兴趣、培养学生概率思维、提升学生探究能力的途径等方面进行探讨，以期为一线教师开展古典概率教学提供参考。

一、古典概率的定义及其内涵

古典概率通常又叫“事前概率”，是指随机事件中各种可能发生的结果及其出现的次数都可以由演绎或外推法得知，无需经过任何统计实验即可计算各种可能发生结果的概率。其定义如下。

若随机试验满足下列条件：

（1）有限性：样本空间Ω只有有限多个样本点；

（2）等可能性：每个样本点出现的可能性相同；则事件A发生的概率为：这个概率称为“古典概率”。

古典概率构造了一种对有限点集的子集“测量”的比例方法。按照这种方法，随机事件的概率可归结为计算事件包含样本点数与样本空间包含样本点数的比值。这种静态的比例计算方法，简单、方便、直观，无须做大量重复的随机试验，概率的许多运算规则也是在这种模型下得到的。

但一个试验是否为古典概型，在于其是否同时具备“有限性”和“等可能性”。随机试验结果的有限性容易判断，但等可能性比较抽象，往往被学生忽视，进而学生时常把“等可能性”游离出古典概率。

二、优化古典概率教学，提升学生探究能力

（一）引导学生探究古典概率的数学内涵

根据随机试验的目的，对样本空间的样本点是否“等可能”进行判断。通过具体实例，循序渐近、由浅入深，破解古典概率“等可能”属性。

例如，连续掷一枚硬币三次，观察每次试验的所有可能结果。用枚举法可得到样本空间为：

Ω1＝｛（正正正），（反正正），（正反正），（正正反），（正反反），（反正反），（反反正），（反反反）｝

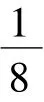
但若将问题改为同时掷三枚硬币一次，观察出现正面或反面次数的所有可能结果。此时，和上述情况不同，用枚举法得到的样本空间为：

Ω2＝｛（三正），（二正一反），（二反一正），（三反）｝

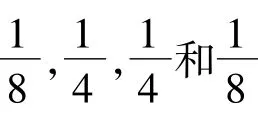
（二）贴近生活，培养学生概率思维

在教学中要充分挖掘能激发学生学习兴趣的素材，激发学生亲自品味探究新事物的乐趣，培养学生用概率的思维去面对各种随机性问题的挑战。

例如【生日问题】美国数学家伯格米尼曾做过一个实验：在一个盛况空前、人山人海的世界杯足球赛赛场上，他随机地在某号看台上，请22个球迷分别写下自己的生日，结果竟发现其中有两人同一天生日。这是巧合还是暗藏有某种必然的规律？

这个问题引起了学生的兴趣，经过思考，学生利用古典概率，给出事件A：“22个球迷中至少有两人同一天生日”，它的概率为：

表达式很清楚，但求出这个具体结果会比较困难。正好留有悬念，让学生猜测这个值的大小，并启发学生探讨：若有r个球迷，结果会如何？按照类比方法，会容易得到事件A：“r个球迷中至少有两人同一天生日”，它的概率为：

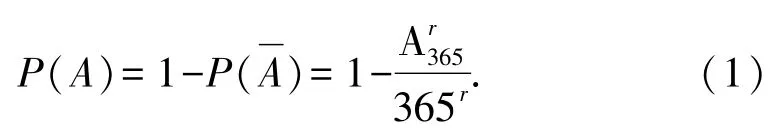
从常规的教学看，（1）式正确。但在将实际问题转化为古典概率时，这个解答存在一定的瑕疵，且往往被学生忽视。首先，球迷的人数r应小于365，（1）式才有意义，否则基于抽屉原理，一定会有两个人生日相同；其次，这个问题能否用古典概率计算，如何保证“等可能”，如何提出满足“等可能”的假设？借助这个具体实例，教师引导学生不要忽视古典概率“等可能”内涵。需要明确，假设“每个球迷的生日在365天的任何一天是等可能的”，才可以用古典概率得到（1）式结果。

就该问题，教师引导学生继续探究：若班级有60名学生，打赌“班级中至少有两人生日相同”对打赌的人是否有利？班级有多少人时，这个问题对打赌的人有利？在学生猜测、讨论，并急切想知道概率结果的情况下，教师把不同的r值与对应的P（A）结果，如表1所示呈现给学生。

看到表1的结果，学生都会感到很惊奇。“22个人中至少有两人同一天生日”的概率居然已达0．476，若班级有23人，打赌说“至少有两人同一天生日”对打赌的人就已经有利。当班级人数达到60人时，几乎可以百分之百地肯定“其中至少有两人同一天生日”。

表1 至少有两人同一天生日的概率

学生对这样的结果感到惊奇，其实更多的是对概率感到神奇。一个60人的班级里，居然可以基本肯定至少会有两个学生生日相同。特别地，当和实际情况对照检验时，发现所在60人的班级中，真的是至少有两名学生生日相同，学生对概率的学习热情高涨起来，再回味这个实例，也理解了概率的作用：概率结果本身虽无法告诉你下一次一定会发生什么事情，也无法替你做决策，但用概率可以预测未来。

（三）挖掘古典概率思政素材，培育学生思辨能力

法国数学家拉普拉斯有句名言：“生活中最重要的问题，绝大部分其实只是概率问题。”这些概率问题又有很多可以用古典概型来描述。通过精心设计的实际问题，引导学生理解并应用古典概率知识求解，其中蕴含的思政元素，既可培养学生的思辨能力，又可以起到对学生思想引领和价值观塑造的作用。

例如【赌博的陷阱】街头有一个摆摊的人，通过有奖摸球设赌。路过的人只要交2元钱就可以参加赌局。摆摊人面前有个袋子，装有8个红球、8个白球。参加者从中随机摸出8个球，当红、白两色球数出现不同比例时，可得到对应奖惩：8∶0奖100元；7∶1奖10元；6∶2奖5元；5∶3奖2元；4∶4罚2元。乍一看，这五种情况中有四种可获得奖励，只有一种会受到惩罚。试问这个游戏真的对参加人有利吗，摆摊人的收益情况又如何？

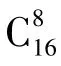
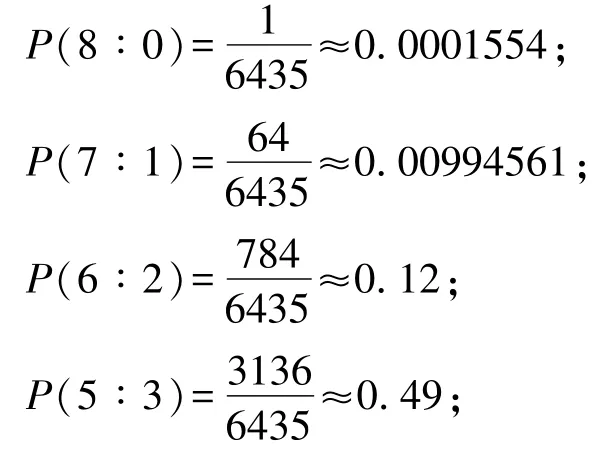
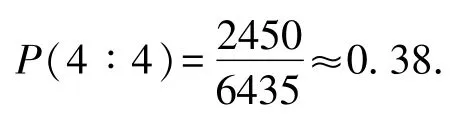
从计算结果看，游戏规则对参加者很不利。参加者基本不可能得到100元和10元。虽然得到2元（本来就是自己的）的概率达到0．49，但出现惩罚2元的概率也达到了0．38。而对摆摊的人，更关心这样的游戏能给他带来多少收益。假设有100人参与，从统计的角度看，平均会有12次6∶2，49次5∶3，38次4∶4，1次7∶1，0次8∶0。于是，摆摊人付给参与人奖金的期望值为92元。而摆摊人从这100个人中实际可得到200元，二者差距一目了然。由此看出，虽然该游戏表面看起来很优惠，但实际上具有很大的欺骗性。这正体现了“随机非随意，概率破玄机。无序隐有序，统计解谜离”。

（四）注重古典概率“由果索因”探索

在古典概率教学中，教师不仅要学生注重“由因索果”的推理，更要学生注重“由果索因”的探索，要强化问题意识，即什么条件可以保证“等可能”，那么如何避免将“等可能”游离出古典概率？教师应引导学生通过提出合理的假设，亲历“等可能”的生成过程，在“等可能”的前提下进行深度探究，从而提升学生的数学核心素养。

例如【女士品茶问题】一位常饮奶茶的女士称，她能从一杯冲好的奶茶中辨别出该奶茶是先放牛奶还是先放茶冲制而成。做了10次测试，结果是她都正确地辨别出来了。问该女士的说法是否可信？

概率可以告诉学生某件事情发生的概率有多大，但如果想检验它预测的对不对，不可能通过一两次试验就能看出来，而是需要大量试验进行检验。基于试验结果对预测进行判断的思维方式，可延伸出数理统计学中假设检验思想：首先提出一个原假设H，假如试验结果与H发生矛盾就否绝原假设H，否则就接受原假设H。

为检验该女士说法是否可信，根据背景，提出原假设H：该女士说法不可信。

只有在此假设下，该女士纯粹是靠运气猜对的，即每次试验的两个可能结果“奶＋茶”或“茶＋奶”是等可能的，才可以用古典概率求解（注：学生一般都没有提出这个假设的意识。同时，若提出假设：该女士说法可信，则两个可能结果“奶＋茶”或“茶＋奶”就不是“等可能”，也就不能用古典概率），具体如下。

10次实验一共有210个等可能结果，而事件A：“能正确分辨出放奶和放茶先后顺序”，它只包含了其中一个样本点，故该女士猜对的概率为：

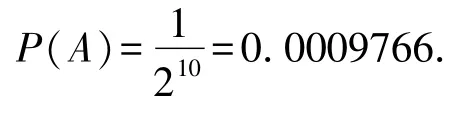
根据“小概率实际推断原理”，概率很小的事件在一次试验中几乎不会发生，但现在该事件竟然发生了，这只能说明原假设H不当，应予否绝，故认为该女士的说法可信。

三、结语

在实际问题中，古典概率“等可能”的属性可基于对称性、均匀性等判断；在理论层面上，可以通过假设检验的思想和方法进行验证。在古典概率的教学中，教师要时刻关注生活中“司空见惯”现象及其背后蕴含的科学道理和逻辑关系并予以提炼，通过精心组织、设计契合古典概率且有新意的实例，让“呆板”的古典概率在丰富的实践中变得栩栩如生、趣味盎然。这样可以在提高学生对古典概率知识的理解及应用的同时，启迪学生的概率思维，强化学生自主提炼“等可能”假设的意识与能力，提升学生的探究能力，最终达到“寓德于教、寓教于乐、乐有所思、思有所得、得有所悟”的教学效果。这也是笔者在常年的概率论与数理统计课程教学中一以贯之、不懈追求的目标。