电子通信信号抗干扰循环频率特征提取算法研究

李相敏, 李相宇, 鄢仁生

(1.长江大学文理学院, 湖北 荆州 434020;2.德州大陆架石油工程技术有限公司，山东 德州 253034;3.中国石油天然气股份有限公司长庆油田分公司第九采油厂,陕西 西安 710000)

0 引 言

随着现代信息技术的发展，人们的生活越来越方便、快捷。电子通信信号为人与人、人与自然的信息交流及传递提供了重要的技术支持。通常超宽带通信需要检测、提取信号，接收方一方面需要对超宽频通信信号进行检测分析与获取；另一方面需要判断通信信号调制方式，进而实现传输信息的提取[1]。从当前电子通信信号提取方式看，主要包括统计特征、似然函数决策理论及数字信号处理(Digital Signal Processing，DSP)三种方法，各有优劣，但容易受到噪声干扰，存在频偏大、定时误差大等不足，达不到电子通信信号提取要求，因此建立电子通信信号抗干扰提取算法尤为重要。电子通信信号特性参数呈现出周期性变化，具有明显的频率特征，因此研究电子通信信号特征提取算法时，从循环频率角度出发来提升提取性能尤为重要。本文首先研究了电子通信信号抗干扰循环频率特征自动调制；然后，分析了小波降噪与协议识别特征；接着，提出了电子通信信号抗干扰循环频率特征自提取流程与方法；最后，给出了实验结果与分析。

1 电子通信信号抗干扰循环频率特征自动调制

本文采用深度学习算法对电子通信信号循环频率特征调制进行特征提取, 使用神经网络的卷积层对样本进行逐层训练；然后采用分类器对样本进行自动识别。使用无监督学习神经网络对标记的样本进行编码，首先在自动编码器中输入五分类标记训练样本数据集，因为自动编码器可在保障建模能力与稀疏性约束的基础上对数据结构进行自动化获取，其基本单元见图1。本研究利用双层自动编码技术完成自动调制与识别，若缺乏分类标签，可采用稀疏自编码器算法由设计编码器训练自编码器，明确各项相关参数，并对编码参数及各个节点的激活值进行记录[2]。自动编码的实现需要两层堆叠数据作为保障，1层主要功能为输出自编码器，2层为接收自编码器，获得新特征下的特征值。若信号向前，输入层的训练样本会向输出层转入，使用全连接层进行特征归一化，然后使用分类器进行分类。若输出层存在实际数据与样本不符，通过交叉熵函数来计算损失，若损失函数的值较大，则说明模型拟合的不好，通过反向传播来调整参数，对各个单元权重予以修正，采用迭代法对各层相关参数与权值进行训练，直到样本真实值和模型预测值的损失较低时，停止训练，得到一个较好的模型[3]。

图1 自动编码机基本单元

2 小波降噪与协议识别特征

2.1 小波降噪原理

作为传统信号去噪法，傅里叶变换法通过对有用信号与噪声的频带分离，将噪声去除后重新构建信号，其能够对带外噪声进行有效的处理，发挥抗干扰作用。小波变换时频分辨率良好，在时频中呈现出表征信号局部特征，即使在低频段也有着较高的分辨率，高频率可以保障高时间分辨率[4]。通常，信号与白噪声实现小波变换后，小波域低频部分是信号的集中区域，高频部分集中了噪声。本研究提出多分辨分析算法(Muti-Resolution Analysis，Mallat)，假设原始信号用f(n)表示，离散时间序列号用n表示，那么Mallat分解算法公式为

(1)

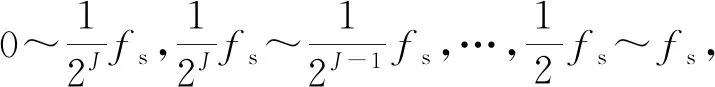
图2 小波降噪流程图

2.2 协议识别流程与改进

在短波通信中，通信协议众多，如何识别这些信号一直是非合作接收方研究的热点。以往多采用待识别信号波形与特征波形的相关系数，是一种常用的协议识别特征，反映了它们的匹配度，其中特征波形主要包含同步码。而短波信道的特点之一是低信噪比，噪声干扰严重，因此导致相关系数较低。短波通信协议相关的同步码、信道探测序列参数是固定的，载波频率产生的波形也是相对固定的，假设f(n)表示特征波形序列，s(n)表示待识别信号序列，其系数公式为

(2)

式中：Cov(f,s)为f(n)、s(n)协方差；D(f)为f(n)的方差。信噪比会直接影响相关系数，导致结果误判，可以通过三种途径进行改进：1)构建降噪后的匹配模板，通过人为高斯白噪声对特征波形的干扰，对不同信噪比下信号实施小波分解，对系数的波动性进行计算，选择较小波动系数，记录其对应位置；2)小波分解待识别信号，将信号数据相同的波形实施分解，并根据匹配对位置信息予以保留；3)协议识别特征提取。对匹配模板数据及相关系数进行计算，作为协议识别特征，实施门限判决，改进后的协议识别流程如图3所示。

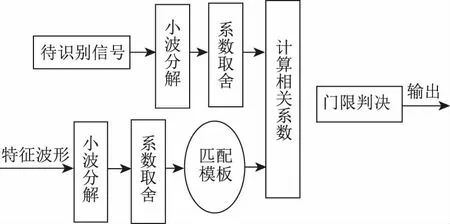
图3 改进后的协议识别流程

2.3 特征波形小波系数取舍

在不同信噪比条件下，小波系数变化小，采用随机序列高斯白噪声，经过分解其在相同位置会呈现出较大的系数变化，因此需要对特征波形进行小波系数取舍，首先需要加扰分解。针对特征波形实施高斯噪声干扰加载，小波分解各信噪比的加扰波形，实现对不同系数的能量归一化。对不同信噪比的最优门限进行设置，比对小波系数与门限值，保留小于门限值的系数。构建新的匹配模板，对同一位置不同信噪比小波系数置零的情况进行统计，取零值提示小波系数波动大，存在噪声系数[5]。

3 电子通信信号抗干扰循环频率特征自提取

3.1 卷积与池化

训练权值在连接神经网络输入与输出节点之间存在，假设m、n分别为输入与输出节点，其处于完全连接网络条件下，m、n值往往较大，存在存储资源浪费的可能。基于此，研究引入了神经网络为核卷积形式，在进行具体操作中能够实现参数共享，输入与输出层可对训练权值进行共享。在具体操作中采用相同的卷积核针对输入层节点实施卷积操作，卷积层规格常见的为2×2或3×3，能够解决资源浪费问题[6]。与全连接网络相比，核卷积网络仅需要少量的存储空间，涉及到的训练操作减少。通过卷积能够获得多个特征图，假设输入二维数据I，使用二维核K，进一步得到

(3)

式中：*为卷积运算。

为减少、压缩特征图，需要进行池化处理，其主要是以某位置相邻输出整体特征对网络在该位置输出进行替代的过程，其在简化数据量的同时，能够对有用的信息予以保留，提升了卷积神经网络(Convolutional Neural Networks, CNN)的抗过拟合能力。假设输入的为二维数据，那么均值池化为

(4)

最大值池化则为

(5)

式中：H为池化窗口高度；W为宽度。

假设2×2池域，其输出池位最大为4个节点，矩阵经过遍历组合为新矩阵，基于位置关系，可以以原矩阵的一半作为输出矩阵，如图4所示。若在数据输入过程中产生翻译现象，可进行汇集处理，避免其影响到网络运行，尽量保障网络输出结果与原数据一致，针对图像中的翻译事件，可通过减少移动，进而降低对操作的影响，体现图像基本特性，避免因位置变化对操作结果的影响，掌握通信信号自提取特点，高频率完成提取。

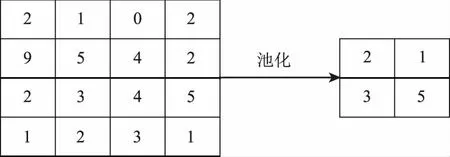
图4 池化过程

3.2 信道重叠信号分离

通常，为提升信号特征自提取的准确性，需要对信道的重叠信号实施分离处理，若接收信号r(t)中存在两个时频重叠信号分量，那么

r(t)=a1(t)cos[φ1(t)]+a2(t)cos[φ2(t)]

(6)

式中：φ1、φ2为时频信号，幅度分别为a1、a2。作为一个窄带信号，信号分量是在常规幅度与频率连续变化条件下产生的，此类信号模式还适用于通信及雷达生成的信号。若信号幅度及频率变化较慢，各个时刻及某一时间段可作为单频信号，此时信号的能量函数与单频信号表达式相同[7]。假设Δt为短时间，可以将单频信号通过电子通信各信号分量表示，可以将接收信号表示为

r(t)=a1(t0)cos[ω1(t0)t+θ1]+a2(t0)·

cos[ω2(t)+θ2]，|t-t0|≤Δt

(7)

式中：ω1,ω2为φ1，φ2的最高频率；θ1、θ2为信号幅度；t0为初始分量。微分方程表示为

r(4)+c1r(2)+c0r=0, |t-t0|≤Δt

(8)

其中，

(9)

(10)

式中：接收信号高阶微分用r(k)表示；c0与c1信号分量瞬时频率存在一定的相关性。根据能量函数能够得到c0与c1的估计值，具体如下。

k阶差分能量算子采用γk[r]=rk-1-rk表示。在计算信号初始分量的瞬时频率时，可采用如下表达式

(11)

获得t0时刻对应的信号分量瞬时幅度、频率后，需要对t0进行一般化扩展处理，获得不同信号分量在各个时间点的瞬时频率与幅度，通过对重构信号分量的评估，能够分离信号分量。上述是针对连续信号分量的分离处理。在对常规信号进行处理时，首先需要实现向离散信号的转变，然后作出相应的处理，对离散情况作出相应的分析，并完成信号分量的分离，其转变公式为

t(n)=a1(n)cos(n)+a2(n)cos(n)

(12)

那么信号分量单频假设，可以用如下公式表示信号分量

[r(n+2)+r(n-2)+r(n+1)+

r(n-1)]+r(n)=0

(13)

通过式(13)可以获得离散信号中不同信号分量在某一时刻以及任何时刻的频率与幅度，并对信号分量进行重构，分离信号分量，使得信号提取结果更加快速、完整。

3.3 信号特征识别与提取

基于电磁环境的复杂性，在进行信号处理时需要精准识别信号调制，维数信号的处理采用时频变换分析法，将其转变为彩色时频图像，图像特征采用卷积神经网络结构进行提取。基于通信信道中循环频率的特点，其能够完成对二相相移键控(Binary Phase Shift Keying，BPSK)、正交相移键控(Quadrature Phase Shift Keying，QPSK)、偏移四相相移键控(Orthogonal Quaternary Phase Shift Keying，OQPSK)以及最小频移键控 (Minimum Shift Keying，MSK)信号的提取，保障信号提取精准性。由于信道混合信号y(t)在不同信号频率段具有一定的差异性，因此设计接收信号频率集合Ay2.0、Ay2.1、Ay4.0，不同信号的循环频率信息均在该集合上。从理论上讲信道混合信号在不同信号频率段的差异性与调制信号难以一一对应，但由于调制信号频率结构独特，如BPSK信号能够对正负对称循环频率予以描述，表示方法为Cx2.1，其二阶循环频率为±1/T，包括了三个等间距频率，这一特征为BPSK信号独有。若循环频率组合与上述约束条件相符，那么可实现对接收信号的判断，明确是否存在BPSK信号。混合信号的BPSK信号可通过二阶循环频率检出，每个信号循环频率均有各自的优势[8]。排除BPSK后，剩余循环频率均来源于QPSK信号，在二阶循环频率方面MSK与OQPSK相同，但在四阶循环频率方面存在一定的差异，因此需要按照顺序识别接收信号MSK、OQPSK信号。MASK信号累积量及特征量如表1所示。

表1 MASK信号累积量与特征量

在特征量A1作用下，能够实现对2ASK、4ASK、8ASK信号的分类，然后利用A2分类识别4ASK信号与8ASK信号。对于2PSK、4PSK、8PSK信号，可以将其四阶累积量特征定义如下：

P=[p1,p2]

其中，

以上，我们从语文课堂互动教学的意义入手，对如何在小学语文课堂中开展互动教学展开了研究。互动式课堂不仅能够唤醒学生的求知欲，还有利于活跃课堂氛围，提高教学效率。为此，教师在具体的教学中，还需要探索更多师生互动、生生互动的方式。

(13)

其对应的累积量、特征量见表2。

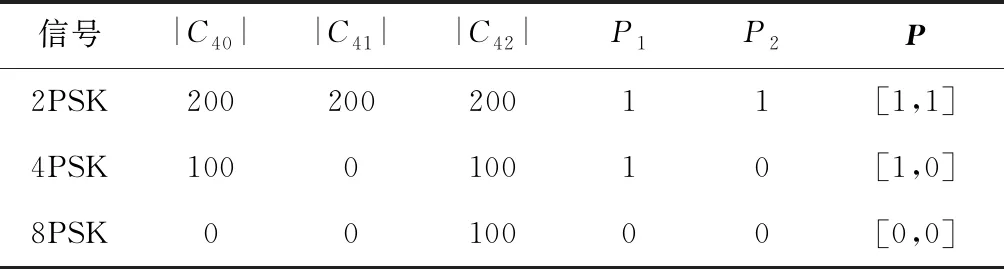
表2 MPSK信号累积量与特征量

在分类MPSK信号时，主要利用特征向量P与欧式距离分类方法，采用如下判决准则：

(14)

在求一阶导数时，含噪MFSK会经过调制转化成为含有幅度信息的信号，经过求导后信号累积方法计算，可以对其模型求一阶导数为

wng(k-nTs)ej(wnk+θ+π/2)]+n′(k)

(15)

为消除δ(k)的影响，可以求中值滤波器的二阶导数来获得信号，计算公式为

(16)

经过变化，MFSK信号累积量呈现出明显的差异性，因此先对基带信号进行微分处理，对4阶累积量进行计算，该方法能够帮助区分2FSK、4FSK、8FSK，其特征量定义为

(17)

可以将通信信号抗干扰循环频率特征提取总结如下：首先，输入采样数据；然后，循环检测频率，计算BPSK信号特征量，当计算结果为1时说明信号循环频率经过提取后得到去除，且对应的BPSK信号特征量已提取。按相同的方法计算QPSK信号特征量，若为1说明去除了此类信号频率，完成电子通信信号抗干扰频率特征提取。

4 实验结果与分析

4.1 降噪性能分析

研究对信号进行仿真试验，设置8PSK信号载波频率为1 800 Hz，码源速率为2 400 B/s，采样率19 000 Hz，共设计三种信号数据，包括64个符号，针对同一序列产生了相应的调制方式信号，经过降噪处理，对比获得不同信号500次试验的结果，如图5，可以发现经过降噪处理的相关值在低信噪比下有着较高的优势，当信噪比为-3 dB时，能够将匹配度控制在20%以上，可降低门限判决漏警率。

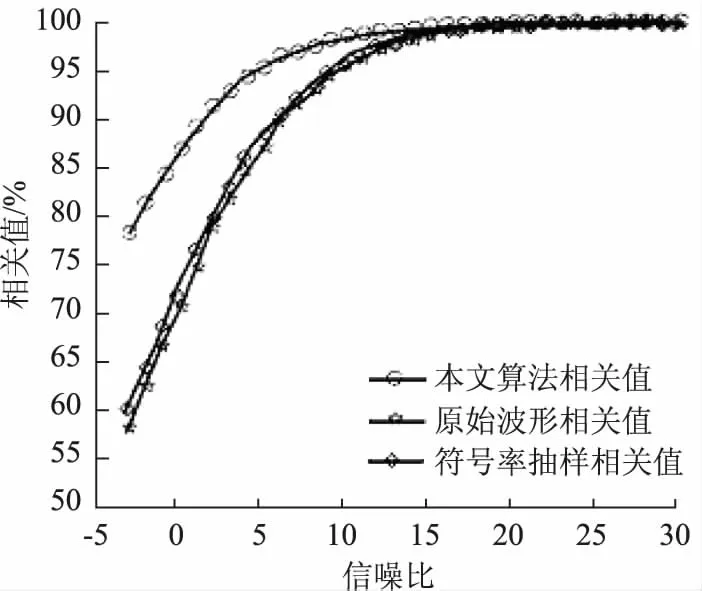
图5 8PSK信号相关值变化曲线

4.2 提取结果完整性与准确性分析

选择Matlab试验平台，设置码源速率为3 Mb/s，信号采样频率设置为120 MHz，对各项特征参数共进行100次实验，提取结果进行分析，可以发现本研究所用方法得到的不同信号分量在任意时刻的瞬时幅度，能够对各个信号分量进行重构，分离信号分量，促进信号提取的实现，保障信号提取的完整性。由图6可知，电子通信信号抗干扰循环频率提取算法准确性均在90%以上，以往的特征提取结果会随着实验次数增多出现波动变化，准确率较低。此次研究将重叠信号作为基础实施分离，并在通信信道循环频率特征提取了BPSK、QPSK、MSK信号，使得信号特征提取结果准确性得到了提升，具有较好的性能，优势明显。

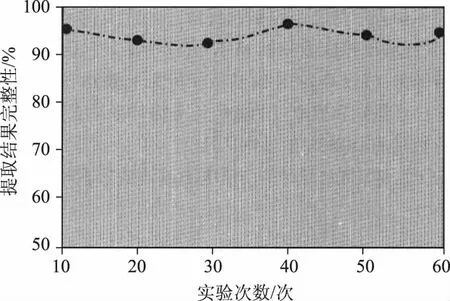
图6 电子通信信号循环频率特征自提取结果分析

5 结 语

电子通信信号抗干扰循环频率特征自提取算法具有一定的优势，能够真正解决电子通信信号频率偏移及时差问题，在保障降噪性能的同时，能够保障提取结果的完整性，提升了电子通信的便利性。但在仿真试验中由于缺乏真实干扰因素，可能存在一定的偏移，今后应不断完善仿真试验方法，深入探索，完善研究成果。